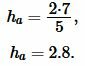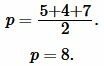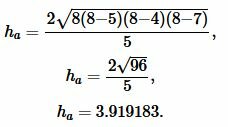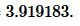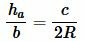Как найти среднюю высоту фигуры - Исправление недочетов и поиск решений вместе с Examum.ru

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Высота треугольника онлайн

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Теорема о пересечении высот треугольника

Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

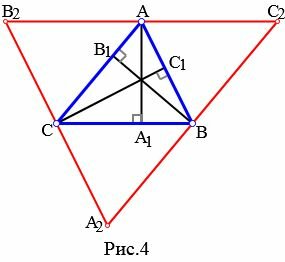
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.

Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

Высота треугольника по основанию и площади

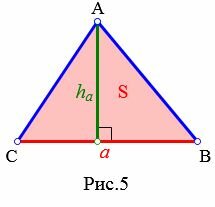
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

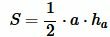
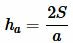(1)

Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.

Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:

Ответ:

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

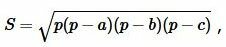(2)

где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:

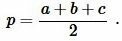(3)

Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

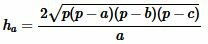(4)

Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):

Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:

Ответ:

Высота треугольника по двум сторонам и радиусу описанной окружности

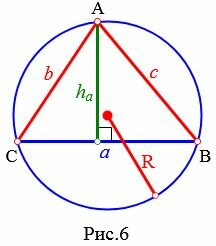
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

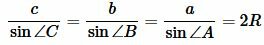(5)

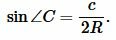(6)

Далее, из теоремы синусов имеем:

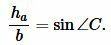(7)

Подставляя (6) в (7), получим:

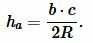(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Проверим сначала условие (9):

(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )

Высота треугольника по стороне и прилежащему к ней углу

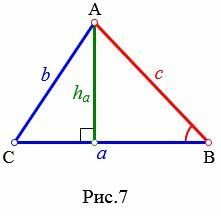
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:

( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )

( small h_a=c cdot sin angle B. )

(11)

Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:

источники:

Формулы для нахождения высоты треугольника

http://matworld.ru/geometry/vysota-treugolnika.php

Источник

Под средней высотой поверхности над уровнем океана понимают среднее
из высот всех элементарно-малых площадок, взятых на этой
поверхности.
Представляя высоту Н поверхности функцией прямоугольных координат
карты
H=F(x, у) (1),
Запишем формулу среднего интегрального значения для двумерной
области d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»005213BB»><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
:

Где — площадь области d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»00B928B4″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
.
Формулу (2)можно представить в таком виде:

Где t wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
— профильные доли области d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»00843A45″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
, заполняющие ее без разрывов и перекрытий.

Формулу (3) можно использовать для определения в том случае, если
область d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»00E55AC0″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
можно так разделить на доли, чтобы определение средней высоты в ней
осуществлялось сравнительно просто.
Например, если за принять участки поверхности, ограниченные
соседними горизонталями, то средние высоты этих высотных поясов
будут равны полусумме отметок окаймляющих участок горизонталей.

Тогда интеграл по области (в скобках формулы 3) можно записать
так:

Где — площадь высотного пояса
И тогда с учетом формулы (4) формула (3) представляется в следующем
виде:

По формуле (5) мы получаем, что измерив площади высотных ступеней и
найдя их средние высоты (полусуммы отметок ограничивающих
горизонталей , получим данные для вычисления средней высоты
заданной области d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»006E429D»><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
.Этот способ называется планиметрическим.
Рассмотрим другой способ, точечный.
Этот способ состоит в том, что на карту наносится произвольная
сетка точек. И тогда за среднюю высоту области d
wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»00A70234″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
принимается среднее арифметическое из высот Нк всех точек, которые
будут находиться в данной области:

Полагая, что высоты сняты в n точках, расположенных в пределах
области d wsp:val=»00FC5C93″/><wsp:rsid
wsp:val=»00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=»00000000″
wsp:rsidRDefault=»00987C1E»><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=»Cambria Math» w:h-ansi=»Cambria Math»/><wx:font
wx:val=»Cambria Math»/><w:i/><w:sz
w:val=»26″/><w:sz-cs
w:val=»26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=»00000000″><w:pgSz w:w=»12240″
w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″
w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″
w:gutter=»0″/><w:cols
w:space=»720″/></w:sectPr></w:body></w:wordDocument>»>
, можно рассчитать ср. кв. ошибку как ошибку репрезентативности
выборки точек по формуле:
Где — ср.кв. отклонение высоты.

Если известна ср. кв. ошибка определения высоты в точках (с учетом
ошибок карты), то соответствующая ошибка ср. высоты:

И тогда общая ср. кв. ошибка средней высоты складываются из :

Или с учетом формул (7) и (9):

Здесь δН можно найти с помощью выборки значений определяется по
нормативным документам для топокарт.
Формула (11) позволяет рассчитать число точек n, необходимых для
определения ср. высоты с заданной , если известны δ Н и mH:

Найдя необходимое число точек n, найдем расстояния между точками,
которое необходимо, чтобы соблюдалась заданная точность:

Где — площадь области .

Понравилась работу? Лайкни ее и оставь свой комментарий!
Для автора это очень важно, это стимулирует его на новое творчество!

Источник

Ответ:

Объяснение:

Средняя высота обозначает, что она по размерам среди 3х высот средняя (логично). То есть средняя высота — это высота опущенная на среднюю по размерам сторону. В данном случае это сторона со значением 33.

Чтобы было понятнее: АВ = 25, ВС = 52, АС = 33, ВD — высота.

DC = x, т.к. большее на АС

Сначала составляем уравнение по теореме Пифагора:

25^2 — (33-х)^2 = BD^2 это первое уравнение

52^2 — x^2 = BD^2 это второе

Т.к. оба равны BD^2 мы можем их приравнять

52^2 — x^2 = 25^2 — (33 — x)^2

625 — (1089 — 66х + х^2) = 2704 — x^2

625 — 1089 + 66х — х^2 = 2704 — х^2

66х = 3168

х = 48 И теперь нам это значение нужно подставить в одну из начальных формул, допустим во вторую

52^2 — 48^2 = BD^2

2704 — 2304 = BD^2

400 = BD^2

BD = 20

Источник

Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
Примеры задач

Нахождение высоты треугольника

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Источник

Высота трапеции

Содержание:

Что такое трапеция
Как найти высоту трапеции
- Через стороны
- Через среднюю линию и площадь
- Через боковую сторону и угол
- Через диагонали, угол между ними и основания
- Через диагонали, угол и среднюю линию
- Через радиус вписанной окружности
Примеры вычисления

Что такое трапеция

Трапеция

Определение

Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.

Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.

Определение

Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти высоту трапеции

Через стороны

Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:

(h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2)

Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь

Если в условии есть данные о величине средней линии и площади, можем использовать формулу:

(h=frac Sm)

Где m — средняя линия трапеции.

Через боковую сторону и угол

Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:

(h=ccdotsinleft(alpharight))

Где alpha — это угол между стороной c и большим основанием a.

Через диагонали, угол между ними и основания

Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:

(h=frac{d_1d_2}{a+b}cdotsinleft(gammaright))

Где (d_1) и (d_2) — диагонали трапеции, а (gamma) — угол между ними.

Через диагонали, угол и среднюю линию

В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:

(h=frac{d_1d_2}{2m}cdotsinleft(gammaright))

Через радиус вписанной окружности

Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:

(h=2r)

Где r — радиус выписанной окружности.

Примеры вычисления

Задача 1

Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и (2sqrt2) см соответственно. Найти высоту.

Решение

Чтобы решить эту задачу, используем формулу (h=sqrt{b^2-(frac{{(a-d)}^2+d^2+c^2}{2cdot(a-b)}})^2.)

Подставляем известные значения:

(h=sqrt{2^2-(frac{{(4,5-2,5)}^2+2^2+{(2sqrt2)}^2}{2cdot(4,5-2,5)}}{)^2=}h=sqrt{4-(frac{4+4-8}4}{)^2=sqrt4=2}) см.

Ответ: h=2 см.

Задача 2

Известно, что основания a и b равнобедренной трапеции равны 3 см и 5 см. Площадь фигуры равна 8 см². Вычислить высоту.

Решение:

Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:

(m=frac{a+b}2=frac{3+5}2=4 см.)

Теперь используем формулу (h=frac Sm) и подставим известные значения:

(h=frac84=2) см.

Ответ: h=2 см.

Задача 3

Мы знаем, что сторона c трапеции равна (sqrt2) см, а угол (alpha) между известной стороной и основанием равен 45 градусов. Найти значение высоты.

Решение:

Используем формулу (h=ccdotsinleft(alpharight)) и подставим значения:

(h=sqrt2cdotsinleft(45^circright)=frac{sqrt2cdotsqrt2}2=frac22=1) см.

Ответ: h=1 см.

Задача 4

Даны диагонали трапеции (d_1) и (d_2), равные 2 см и 3 см, а также угол gamma между ними, который равняется 30 градусов. Основания a и b, длина которых 2 см и 1 см соответственно. Найти h.

Решение:

Для решения задачи использует формулу (h=frac{d_1d_2}{a+b}cdotsinleft(gammaright).)

Подставим значения:

(h=frac{2cdot3}{2+1}cdotsinleft(30^circright)=frac63cdotfrac12=1) см.

Ответ: h=1 см.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник