Как найти стабилизирующее управление

УДК 62.50 ББКЖ30

СТАБИЛИЗИРУЮЩЕЕ СЕТЕВОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ ДИСКРЕТНЫМИ СИСТЕМАМИ В УСЛОВИЯХ ПОТЕРИ ПАКЕТОВ ДАННЫХ1

Жучков Р.Н.2, Пакшин П. В.3

(Арзамасский политехнический институт (филиал) Нижегородского государственного технического университета им. Р. Е. Алексеева)

Рассматривается линейная система, в которой объект управления и регулятор обмениваются информацией через сетевой канал связи. Решается задача стабилизации в условиях возможных потерь пакетов данных, которые моделируются марковской цепью. Рассматриваются случаи обратной связи по состоянию и по измеряемому выходу. В обоих случаях эффективно используется техника линейных матричных неравенств.

Ключевые слова: линейные дискретные системы, сетевое стабилизирующее управление, потери пакетов, марковская модель, линейные матричные неравенства.

Введение

В классической теории управления предполагается, что информация об измеряемых координатах объекта управления может быть мгновенно получена и мгновенно использована для формирования управляющего воздействия. Однако в последние годы получили широкое распространение системы, в которых способ обмена данными играет существенную роль. К таким относятся

1 Работа выполнена при финансовой поддержке РФФИ, гранты 10-08-00843_а, 11-01-97025-р_поволжье_а.

2Роман Николаевич Жучков, аспирант, (romanjkv@mail.ru)

3 Павел Владимирович Пакшин, доктор физико-математических наук, профессор, (pakshinpv@gmail.com).

системы управления удаленными объектами по беспроводным каналам с ограниченной пропускной способностью, системы управления движением в транспортных сетях и т. д. [8]

В связи с этим в настоящее время стала активно развиваться теория сетевого управления, посвященная исследованию систем управления, в которых объект управления и регулятор обмениваются информацией через сетевой канал связи с ограниченной пропускной способностью.

Необходимость учета информационных ограничений при использовании сетевых каналов вносит существенные особенности в решение задачи синтеза стабилизирующего управления с обратной связью [1, 8]. В самом деле, если скорость передачи данных по каналу недостаточна, задача управления при использовании этого канала неразрешима в принципе. Таким образом, возникает глобальная задача определения границ скорости передачи данных в информационных каналах систем сетевого управления. После того как эта задача будет решена, необходимо учесть эффекты запаздывания, квантования и потери пакетов в процессе передачи квантованных сигналов. Перечисленные эффекты могут привести к существенному ухудшению качества переходных процессов и даже к неустойчивости [9].

В данной работе рассматривается дискретная система с управлением через сетевой информационный канал с учетом только одного фактора — потери пакетов данных. Процесс потери пакетов моделируется марковской цепью. Ставится задача синтеза управления с обратной связью по выходу, обеспечивающую экспоненциальную устойчивость системы в среднем квадратиче-ском.

При решении задач синтеза с учетом этого фактора в настоящее время используются различные подходы: в работе [6] используются идеи выпуклого анализа для решения билинейного матричного неравенства, из которого находится стабилизирующее управление; в [7] используются идеи оптимизации; в [5] задача синтеза управления с обратной связью по вектору состояния сводится к решению линейного матричного неравенства. Суще-

ствующие результаты по синтезу управления с обратной связью по выходу не доведены до эффективных алгоритмов. В данной статье предлагается относительно простая идея искусственного разделения задач оценивания и управления для систем случайной структуры, которая сводит задачу синтеза стабилизирующего регулятора к решению линейных матричных неравенств.

1. Линейные системы с доступным измерению вектором состояния

Рассмотрим линейную дискретную систему, описываемую разностным уравнением:

(1) хк+1 = Ахк + Бпк,

где Хк — п-мерный вектор состояния; ик — т-мерный вектор управления. Закон управления формируется в виде обратной связи по состоянию

(2) ик = -Охк

и обмен информацией между объектом (1) и регулятором (2) осуществляется через сетевой канал связи, в котором может происходить потеря пакета данных (рис. 1). Предполагается, что потерянный пакет не может позднее придти ни на сторону объекта ни на сторону регулятора, т. е. происходит абсолютная потеря. Задача состоит в нахождении такой матрицы усиления О, при которой управление в (2) обеспечивает устойчивость замкнутой системы при указанных условиях потери пакетов данных. При

сделанных предположениях в каждый дискретный момент времени рассматриваемая система может находиться в двух структурных состояниях. В первом обмен информацией между объектом и регулятором осуществляется нормально, во втором пакет теряется либо при передаче на сторону объекта, либо при передаче на сторону регулятора. Будем считать, что в случае потери пакета управление на объект не подается и что переход из одного структурного состояния в другое описывается марковской цепью с известной стохастической матрицей. Таким образом, модель системы с учетом возможных потерь пакетов можно описать

Объект управлении

щ — — Лхк +Вик ч

ч Канал обмена данными (сеть) 4

<3

Регулятор

Рис. 1. Схема сетевой системы управления

следующими уравнениями

(3) б! : хк+1 = Ахк + Бпк,

£2 : Хк+1 = Ахк.

Структурные состояния £1 и £2 будем рассматривать как возможные состояния марковской цепи г к, к = 0,1,… с вероятностями перехода р^ = Р [гк+1 = Sj | г к = £»]. Относительно простая стратегия, приводящая к модели (3) представляется вполне разумной при достаточной надежности канала связи, даже если разомкнутая система неустойчива.

Поскольку модель (3) является стохастической, необходимо соответствующим образом ввести понятие устойчивости. Достаточно сильным и адекватным рассматриваемой задаче является понятие экспоненциальной устойчивости в среднем квадратиче-ском (ЭУСК) [3].

Определение 1. Система (3) называется экспоненциально

устойчивой в среднем квадратичном, если существуют числа в > 0 и 0 < ( < 1 такие, что

М[|| хк ||2| Хо = х] < в II х У2 Ск,

где М — оператор математического ожидания. Необходимые и достаточные условия ЭУСК дает следующее утверждение [3]. 116

Теорема 1. Для экспоненциальной устойчивости в среднем квадратическом системы (3) необходимо и достаточно, чтобы существовала квадратичная форма V(х, г) = xTHiХ, Нг = Нт > 0, г = 1, 2, такая, что

М^(хк+1, Гк+1 | Хк = х, Гк = г)] — V(х, г) < 0, г = 1,2.

Будем искать управление (2) из условия ЭУСК системы (3). Применяя теорему 1, получим, что матрица усиления должна удовлетворять следующей системе матричных неравенств:

(4) (А — ВО)т(Н1рп + И2Р12)(А — ВО) — И1 < 0

(5) АТ(Н1Р21 + Н2Р22)А — Н2 < 0,

где Н1, Н2 — неизвестные симметричные положительно определенные матрицы; матрица О — искомая матрица усиления обратной связи.

Неравенство (4) может быть сведено к линейному умножением справа и слева на X = Н—1 и заменой Х2 = Н2, У = ОХ1 Применяя теорему о дополнении Шура, получим следующую систему линейных матричных неравенств:

— X ^Рйг(х1,У)т уР2Г(хьу)т» уРГТ(хьу )

— Х2 уРТАХ

где Г(Х1, У) = АХ1 -ВУ. Неизвестные матрицы в данной системе могут быть легко найдены средствами существующих пакетов решения линейных матричных неравенств [4].

Х1 0

0

Х2

> 0,

-Х1

— Х2

< 0,

0

2

0

2

2. Линейные системы с управлением по вектору измерений

В данном разделе рассмотрим случай, когда вместо вектора состояния прямому измерению доступен вектор

(6)

У k = Cxfc.

В этом случае для построения стабилизирующего управления будем использовать обратную связь по оценке вектора состояния на основании доступных измерений.

Оценку вектора состояния будем искать в следующем виде:

(7) Xk+i = AXk + Buk + K(yk — Cxk),

где K — неизвестная матрица. Стабилизирующее управление запишется как

(8) uk = —GXk.

В каждый момент времени замкнутая система может находиться в одном из следующих структурных состояний:

«(A — BG) —BG 0 (A — KC)

(9)

(10)

S1 : Xk+1 =

_Xk+i_

Xk

Xk_

S2 :

Xk+1 A 0 Xk

_Xk+i, 0 A .Xk.

где Хк = хк — хк.

Примем далее гипотезу о возможности разделения переменных х и х для того, чтобы получить отдельные соотношения для матриц усиления и наблюдателя. Эта гипотеза, справедливая для линейных систем постоянной структуры [2], в рассматриваем случае нуждается в проверке. После нахождения матриц К и О необходимо подставить их в (9)-(10) и проверить устойчивость полученной системы. Такой подход представляется вполне обоснованным с точки зрения эффективности использования аппарата линейных матричных неравенств.

После разделения переменных в системе (9)-(10) получим

(11) (12) 118

51 : Xk+i = (A — BG)xk,

52 : Xk+i = Axk,

(13)

(14)

51 : Жк+1 = (А — КС)хк,

52 : Жк+1 = Жк.

Как и в предыдущем случае воспользуемся результатом теоремы 1. В результате получим следующие матричные неравенства для нахождения неизвестных матриц О и К:

(15) (А — БО)т(Я1рц + Я2Р12ХА — ВО) — Н1 < 0,

(16)

Ат (Я1Р21 + Я2Р22)А — Я2 < 0;

(17) (А — КС)т(#1Ри + Я2Р12ХА — КС) — #1 < 0,

(18) (#1Р21 + Н2Р22) — Н2 < 0.

Неравенство (15) умножим справа и слева на Н-1, а в неравенстве (17) заменим Н1 на Н 1. После таких преобразований неравенства (15) и (17) примут следующий вид:

-1

(АХ1 — ВГ)1Х1-1ри(АХ1 — ВГ1) +

(19) +(АХ1 — ВГ1)тХ2-1р12(АХ1 — ВЦ) — X < 0,

(НН1А — У1СГя-Ч^А — Г1С) + (20) +(Н2А — Г2С)тН2-1Р12(Я2А — У2С) — Н < 0,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где Х1 = Н-1, Х2 = Я2-1, Г = Х1О, Г = НН1К, Г2 = Н2К.

Воспользуемся теоремой о дополнении Шура [4], чтобы привести неравенства (19)-(20) к линейным. В результате получим:

(21)

(22)

(23)

(24)

^(ХьИ)

» -Х2

Г(Х1,Г1)т

X 0

0 Х2

АХ2 АХ2

-Х1 0

Н

^(Н 1, г ) Я2Л(й 1,Г)

р?1Л(НН 1,Г )т

Н1 0

0

— Х2

^(Я 1,Г )т 0

Н2

> 0,

< 0,

> 0,

(Н1Р21 + Й2Р22) — #2 < 0,

где Л(ЯЬ У) = НA — УС и Г(ХЬ У1) = АХ — BY1. Из линейных неравенств (21)-(24) теперь можно найти матрицы О и К для разделенной системы (11)-(14). Если при этом система (9)-(10) является устойчивой, то гипотеза о разделении справедлива и указанные матрицы являются искомыми матрицами усиления для исходной задачи. Для проверки устойчивости системы (9)-(10) подставим полученные матрицы в систему (9) и воспользуемся результатом теоремы 1 с функцией Ляпунова вида V(х, г) = х]:,Нгк, где гк = [хк хк] и Н = Нт > 0 В итоге получим, что необходимо проверить совместность следующих линейных матричных неравенств: (25) рпАтЯ 1А + Р12Ат^А — Я1 < 0,

(26) где

Р21Я1 < ^2(1 — Р22),

(27)

А =

(А — БО) -БО 0 (А — КС) Разрешимость полученных неравенств зависит от значений р^. Может оказаться, что при определенных значениях этих вероятностей построение стабилизирующего управления невозможно.

3. Пример

В качестве модельного примера была рассмотрена следующая система

хк+1

1 0,8 0 0,5

0,8 0 1 хк + 1

-3,1 — 2,7 1,2 0,7

1 0 1″

Ук = 0 10 хк

ик

Матрица Р задавалась в следующем виде:

(28) 120

Р

V

1 — р 1 р 1 1 — р 1 р 1

Рис. 2. Схема моделирования

т. е. предполагалось, что условные вероятности состояний $1 и $2 одинаковы.

Исходная система в разомкнутом состоянии является неустойчивой, вектор ее собственных значений равен [1,3532; -0,1766 — 1,2028г; -0,1766 + 1,2028г]т.

На рис. 2 представлена схема моделирования в SIMULINK. Рис. 3-5 содержат графики переходных процессов моделируемой системы.

Были рассмотрены значения условной вероятности потери пакета Р1 равные 0,1, 0,2 и 0,25, для них получены следующие матрицы усиления О и К:

Сод = [-0,3306 1,1745 0,7966] ,

0,2475 0,9578 1,6791 » 0,7391 0,0103 -2,8177 ,

Оо,2 = [-0,2221 1,1789 0,7597] ,

КТ1 =

Рис. 3. Переходные процессы при вероятности потери пакета

равной 0,1

<Т2 = 0,2450 0,8811 0,9514 -0,0173 1,6555 -2,5508

С0,25 = [0,0596 0,9601 0,7801] ,

КТ = к0,25 = «0,2625 0,9747 0,9287 -0,0726 1,6924 » -2,2852

которым соответствуют следующие собственные значения матрицы (А — ВС):

Еод = [0,3455 — 0,5906г 0,3455 + 0.5906г -0,0577] ,

Ео,2 = [0,5375 — 0,4708г 0,3455 + 0,5906г -0,2305] , Ео,25 = [0,3326 — 0,8141г 0,3326 + 0,8141г -0,0012] ,

Рис. 4. Переходные процессы при вероятности потери пакета

равной 0,2

и матрицы (А — В К):

Код = [0,2873 —0,0247 0,0003] ,

Ео,2 = [0,2809 0,0346 0,0013] ,

Ко,25 = [0,2093 0,0541 — 0,0751г 0,0541 + 0,0751г] .

С увеличением условной вероятности потери пакета собственные значения замкнутой системы все более смещаются к границе устойчивости. При этом переходные процессы становятся более колебательными и увеличивается их время (рис. 3-5).

При условной вероятности потери пакета данных более 0,25 матричные неравенства (21)-(24) становятся несовместными, и система не может быть стабилизирована в рамках принятой структуры управления.

Рис. 5. Переходные процессы при вероятности потери пакета

равной 0,25

Литература

1. АНДРИЕВСКИЙ Б.Р., МАТВЕЕВ А.С., ФРАДКОВ А.Л.

Управление и оценивание при информационных ограничениях: к единой теории управления, вычислений и связи (обзор) // Автоматика и телемеханика. — 2010. — №4. -С. 34-99.

2. ОСТРЕМ К.Ю. Введение в стохастическую теорию управления. — М.: Мир, 1973.

3. ПАКШИН П.В. Дискретные системы со случайными параметрами и структурой. — М.: Физматлит, 1994.

4. ЧУРИЛОВ А.Н., ГЕССЕН А.В. Исследование линейных матричных неравенств. Путеводитель по программным

пакетам. — СПб.: Изд-во С.-Петерб. ун-та, 2004.

5. HONGO S., LI Y., ZHANG W. Stabilization of Networked Control Systems with Communication Constraints and Packet Dropouts // 48th IEEE Conference on Decision and Control. -2009. — P. 7936-7941.

6. DAClC D., NECSlC D. Quadratic stablization of linear networked control systems via simultaneous protocol and controller design // Automatica. — 2007. — Vol. 43. — P. 11451155.

7. NILSSON J., BERNHARDSSON B. LQG Control Over a Markov Communication Network // Proceedings of the 36th IEEE Conference on Decision and Control. — 1997. — Vol. 5. -P. 4586-4591.

8. ZAMPIERI S. Trends in Networked Control Systems // 17th IFAC World Congress (IFAC’08). — 2008. — P. 2886-2894.

9. ZHANG W., BRANICKY M., PHILIPS S. Stability of Networked Control Systems // IEEE Control Systems Magazine. — 2001. — P. 84-99.

STABILIZING NETWORKED CONTROL OF LINEAR DISCRETE-TIME SYSTEMS WITH PACKET DROPOUTS

Roman Zhuchkov,post-graduate student (roman_jkv@mail.ru), Pavel Pakshin, Dr.Sci., professor, Arzamas Polytechnic Institute of R.E. Alekseev, Nizhny Novgorod State Technical University, 19, Kalinina Street, Arzamas, 607227, Russia, (pakshinpv@gmail.com).

Abstract: For a linear system where a plant and a regulator communicate over a network a stabilization problem is solved in the presence of possible packet dropouts. Dropouts are modeled with a Markovian chain. Cases ofstate-based and output-based feedback are studied. In both cases LMI technique proved to be efficient.

Keywords: linear discrete systems, networked stabilizing control, packet dropouts, Markovian model, linear matrix inequalities.

Статья представлена к публикации членом редакционной коллегии А. П. Курдюковым

На примере простой механической системы посмотрим, как «оживить» картинки в Scilab без дополнительных плагинов и без использования comet().

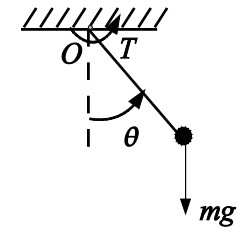
Будем стабилизировать простой математический маятник.

Рисунок. Математический маятник.

Уравнения которого имеют вид.

( ddot{theta} + bdot{theta} + asintheta = cT )

Стабилизировать маятник будем в программной позиции ( theta = delta=const ) с помощью вращающего момента: ( T = u )

( ddot{theta} + bdot{theta} + asintheta = cu ) (1)

Найдём программное управление ( u^p )

Программное управление ( u^p ) — это управление, которое обеспечивает программную позицию, т.е. отклоняет маятник на угол ( delta ). Подставим ( theta = delta ) в (1):

( ddot{delta} + bdot{delta} + asindelta = cu^p )

Так как угол ( delta ) — это постояннная величина, ведь мы хотим, чтобы маятник остановился в таком положении, её производные будут равны 0, следовательно:

( 0 + 0 + asindelta = cu^p )

Откуда можно выразить искомое программное управление ( u^p ):

( u^p = frac{a}{c}sindelta) (2)

Перейдём к системе д.у.

Подробно переход к системе ДУ рассматривается в этом материале.

Введём фазовые координаты:

( x_1 = theta, x_2 = dot{theta} )

Тогда исходное уравнение (1) второго порядка сведётся к системе из двух дифференциальных уравнений первого порядка:

begin{cases} dot{x_1} = x_2 \ dot{x_2} = cu — bx_2 — asinx_1 quad (3)end{cases}

Программная позиция для системы

Наша задача — обеспечить скорейшую остановку маятника в заданной позиции, т.е. перевести маятник в позицию ( theta = delta ), где скорость=0. Запишем это условие для фазовых координат

( x_1 = delta, x_2 = dot{delta} = 0 )

Итак, для системы (3) нас интересует позиция:

begin{cases} dot{x_1} = delta \ dot{x_2} = 0 quad (4) end{cases}

Для того, чтобы к системе (3) можно было применят теоремы об асимтотической устойчивости нулевого положения равновесия, нам неоходимо перенести систему коордиинат в точку, где позиция ( (delta, 0) ) — это нуль.

Переход к системе в отклонениях

Введём отклонения от программной позиции (4) в системе (3):

begin{cases} y_1 = x_1 — delta \ y_2 =x_2 — 0 end{cases} (5)
begin{cases} x_1 = y_1 + delta \ x_2 =y_2 end{cases}

Подставим (5) в (3), тогда система в отклонениях примет вид:

begin{cases} dot{y_1} = y_2 \ dot{y_2} = cu — by_2 — asinleft( y_1 + delta right) end{cases}

Корректировка управляющего воздействия

Как правило, для эффективного управления динамическими системами одного программного управления ( u^p ) бывает недостаточно из-за неточностей в измерениях и влияния внешних источников, поэтому мы введём добавочное стабилизирующее управление ( u^{st}) :

( u = u^p + u^{st} )

Тогда системе в отклонениях получим:

begin{cases} dot{y_1} = y_2 \ dot{y_2} = cleft( u^p + u^{st} right) — by_2 — asinleft( y_1 + delta right) end{cases}, или
begin{cases} dot{y_1} = y_2 \ dot{y_2} = c cdot frac{a}{c} sindelta + c cdot u^{st} — by_2 — asinleft( y_1 + delta right) end{cases}, что приводит к
begin{cases} dot{y_1} = y_2 \ dot{y_2} = asindelta + cu^{st} — by_2 — asinleft( y_1 + delta right) quad (6) end{cases}

Линеаризация системы в отклонениях

Так как эффективнее всего теоремы об устойчивости работают для линейных систем, начнём с линеаризации системы (6).

Разложжим ( sinleft( y_1 + delta right) ) в окрестности нуля:

( sinleft( y_1 + delta right) sim y_1cos(delta) + sindelta )

Подставляя данное разложение в (6), получим:

begin{cases} dot{y_1} = y_2 \ dot{y_2} = asindelta + cu^{st} — by_2 — ay_1cos(delta) — asindelta end{cases}

Таким образом, система (6) примет вид:

begin{cases} dot{y_1} = y_2 \ dot{y_2} = — acos(delta)y_1 — by_2 + cu^{st} quad (7) end{cases}

Запишем систему (7) в векторно-матричном виде, чтобы с ней было бы удобнее работать:

begin{matrix}
dot y= { begin{pmatrix} 0 & 1 \ — acos(delta) & -b end{pmatrix} } y + { begin{pmatrix} 0 \ c end{pmatrix} } u^{st} quad (8)
end{matrix}

Найдём стабилизирующее управление (u^{st} )

Прежде всего, сделаем из системы (8) однородную систему. Для этого выберем (u^{st} ) вида:

( u^{st}= -Ky, quad K = (k_1, k_2) quad (9) )

и подставив (9) в (8), получим чудесную линейную однородную систему дифуров:

begin{matrix}
dot y= { begin{pmatrix} 0 & 1 \ — acos(delta)-сk_1 & -b-ck_2 end{pmatrix} } y quad (10)
end{matrix}

Стабилизиирующее управление (u^{st} ) — это управление, которое стабилизирует систему. То есть обеспечивает асимтотическую устойчивость нулевого положения равновесия этой системы.

В обычных условиях, система (10) сосвем не обязательно будет ас. устойчивой, но чтобы победить эту несправедливость мы и ввели управление (u^{st} ) в виде ( u^{st}= -Ky ), подрегулировав значения (k_j ) которого, мы добьёмся того, чтобы корни характеристического уравнения системы (10) были бы «левыми».

Значения (k_j ), кстати, называются коэфффицентами усиления.

Итак, нам предстоит найти условия на основе (k_j ), при которых собственные значения матрицы

begin{matrix}
{ begin{pmatrix} 0 & 1 \ — acos(delta)-сk_1 & -b-ck_2 end{pmatrix} } quad (11)
end{matrix}

были бы расположены в левой полуплоскости комплекной плоскости.

Условия гурвицевости матрицы (11)

Чтобы не утруждаться поиском с.з. и с.в. матрицы (11), воспользуемся критерием асисмтотической устойчивости вида:

begin{cases} trA < 0 \ |A| > 0 end{cases}

Откуда получим условия на (k_1 ) и (k_2 ) :

begin{cases} k_2 > -frac{b}{c} < 0 \ k_1 > frac{a}{c}cos(delta) end{cases}

Итак, выбирая стабилизирующее упарвление в виде:

(u^{st} = -k_1y_1 — k_2y_2 )

мы добьёмся стабилизации линейной системы в отклонениях (7), что, в свою очередь будет значить схождение моделируемого движения маятника к программной позиции при решении задачи стабилизации положения равновесия, где управление будет складываться из программного и стабилизирующего управлений

(u = u^p + u^{st} )

Программная реализация

Приступим, наконец, к моделированию процесса стабилизации математического маятника в Scilab. Для этого нам понадобятся:

• Система (3)
• Управление (2)
• Управление (12)
• Замена (5)

Сначала зададим параметры, фигурирующие в системе:

g = 9.8;

m = 2;
k = 0.9;
L = 3.5; 

b = k/m;
a = g/L;
c = 1/(m*L*L);

Параметры математического маятника.

Далее зададим программное положение (delta ) и пaраметры стабилизирующего управления (k_j ):

delta = %pi/5; 
  
k1 = .1; 
k2 = 10;

Программная позиция и коэффициенты усиления

Зададим начальные условия, шаг дискретизации и отрезок интегрирования для решения системы ОДУ в Scilab:

Xo = [2.1; 0.5]; // Здесь первые два элемента - это н.у. (координата и скорость)
tmax = 20;
t0 = 0;
t = 0:1e-2:tmax;
X = ode(Xo, t0, t, systNelin);

параметры для решения системы дифуров в Scilab.

И, наконец, запишем функцию, которая отвечает за формирование системы дифуров, описывающих движение маятника с найденным управлением:

function dx = systNelin(t, x)
    y(1) = x(1) + delta;
    y(2) = x(2);
    
    Up  =  a/c * sin(delta);    
    Ust = -k1*y(1) - k2*y(2);
    U   =  Up + Ust;    
    
    dx(1) = x(2);
    dx(2) = c*U - b*x(2) - a*sin(x(1));  
endfunction

функциия системы ОДУ в Scilab.

Этого, в принципе, достаточно, чтобы получить статическую графическую интерпретацию решения нашей задачи.

subplot(121);
xgrid();xtitle("Угол отклонения маятника", "$Large t$", "$Large theta$");
plot(t, t*0 + delta,'r--');
plot(t, X(1,:),'b');
gca().children.children(1).thickness = 2; 
legend('$delta$','$theta$');

subplot(122);
xgrid();xtitle("Скорость маятника", "$Large t$", "$Large dottheta$");
plot(t, t*0 + 0,'r--');
plot(t, X(2,:),'b');
gca().children.children(1).thickness = 2; 
legend('$dotdelta$','$dottheta$');

вывод графиков с настройкой толщины в Scilab.

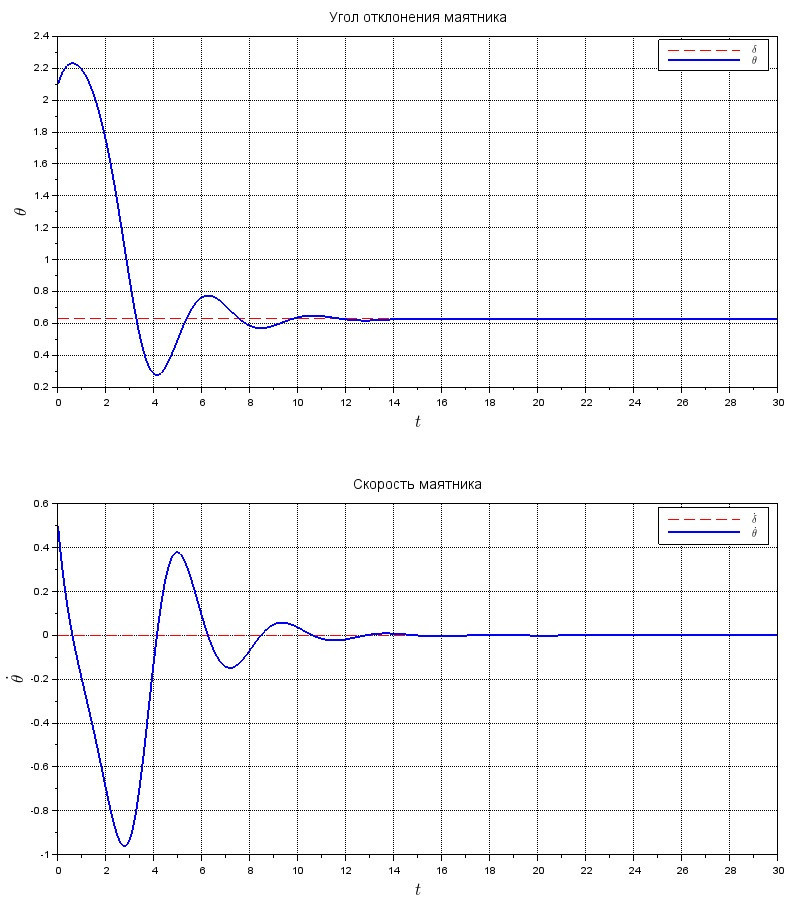
Координата и скорость маятника под действием управления, (к1, к2) = (0.1, 10)

При этом, подправляя коэффициеты усиления, можно регулировать скорость сходимости.

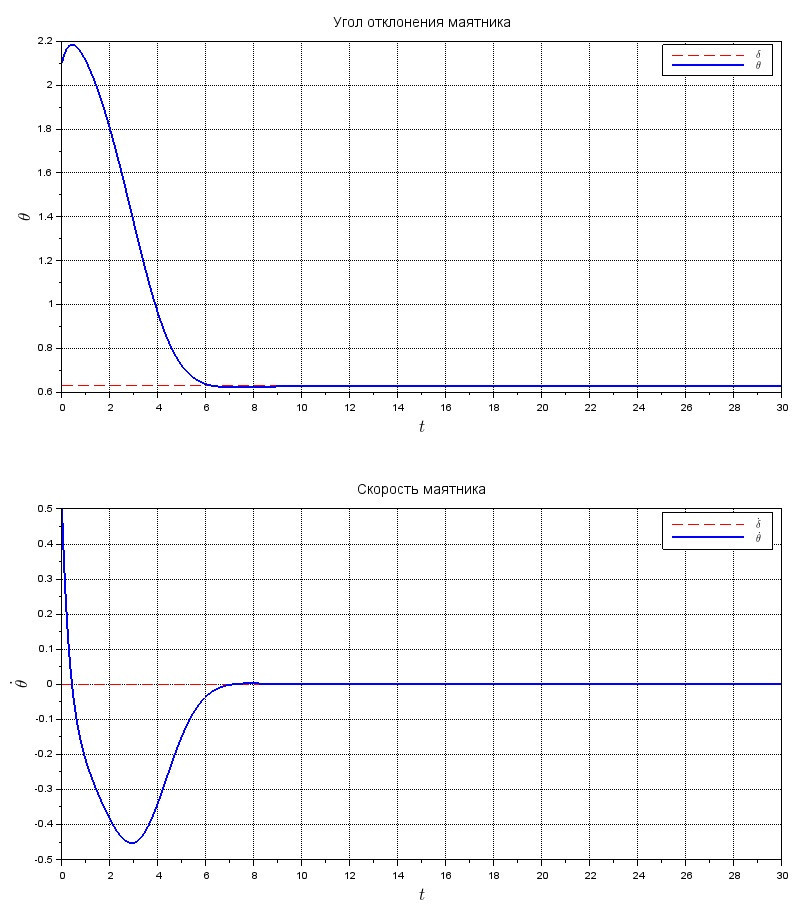
Координата и скорость маятника под действием управления, (к1, к2) = (0.1, 50)

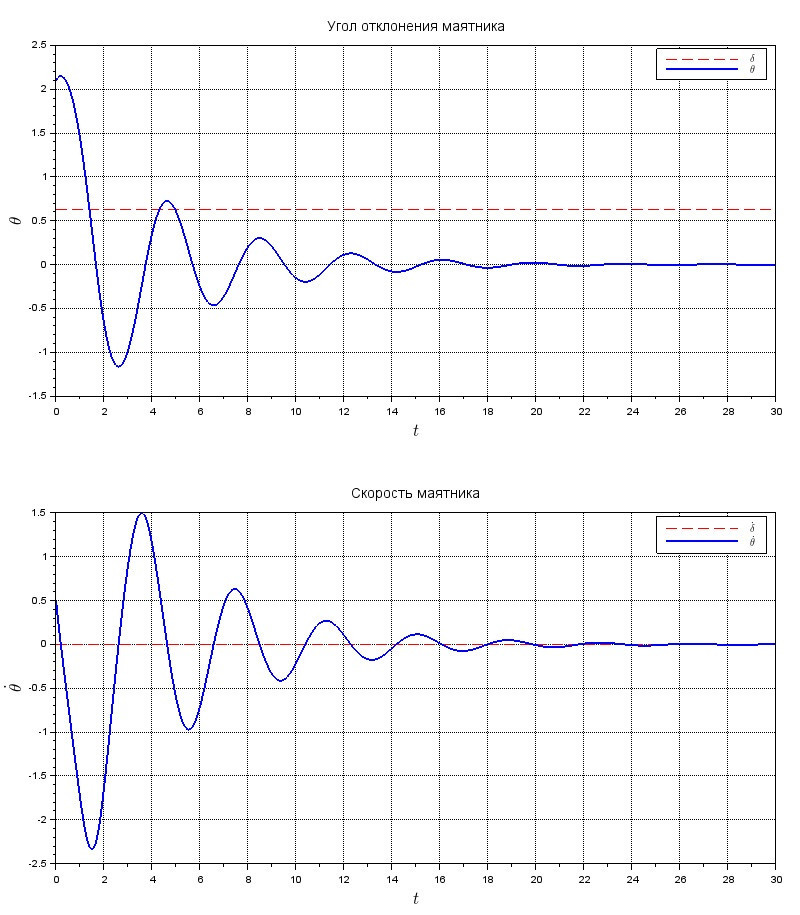
При этом, без управления маятник будет бултыхаться довольно долго и остановится в устойчивом положении равновесия (0,0):

...
  U   =  0;    
...

отключим управление в функции системы ОДУ

Координата и скорость маятника без управляющего воздейсвтия

Создание анимации движения в Scilab

Пойдём дальше и приступим к реализации движущегося объекта.

Для начала, повернём сетку координат на 90 градусов, чтобы маятник смотрела вниз

X_r = X - %pi/2;
delta_r =  delta- %pi/2;

новые координаты.

Добавим звёздочки на координатную сетку — начальное положение и программную позицию маятника

plot(L*cos(X_r(1,1)), L*sin(X_r(1,1)), 'b*'); 
plot(L*cos(delta_r), L*sin(delta_r), 'r*'); 
legend('начальное положение', "программная позиция");
xtitle('Математический маятник');
xgrid;

начальное и конечное положения маятника

И изобразим маятник в исходном положении с помощью ломаной линии с координатами ( (0, 0) — ( L*cos(X_r(1,1)), L*sin(X_r(1,1)) ) ):

x_ = [0; L*cos(X_r(1,1))];
y_ = [0; L*sin(X_r(1,1))];
xpoly(x_, y_, "lines", 0);

рисуем прямую в Scilab.

Далее отредактируем параметры элемента xpoly(). Наличие соединений mark имитирует груз на конце стержня маятника, mark_style = 9 говорит, что это кружочек, а mark_offset = 1 отвечает за смещение кружочка относительно линии:

pendulum = gce(); 
pendulum.foreground = 1;
pendulum.thickness  = 2;
pendulum.mark_style = 9;  
pendulum.mark_offset = 1;

рисуем прямую в Scilab.

Прямая с кружочком

Приступим к имитации движения маятника. Его траектория — это решени системы ОДУ, т.е. элементы матрицы X_r. В первой строке этой матрицы содержится координата маятника ( X_1 = theta ) в момент времени ( i ), а во второй строке — скорость маятника ( X_2 = dottheta ) в этот момент времени. Нам нужна координата для изменения позиции палочки с кружком, причём, центр маятника так и будет оставаться в положении ( (0,0) ), двигаться же будет его не закреплённый конец:

i = 1;
while i<=length(t)   
    drawlater();    
        sca(pendulum_axes);   
        x_ = [0; L*cos(X_r(1,i))];
        y_ = [0; L*sin(X_r(1,i))];        
        pendulum.data = [x_, y_];     
    drawnow();    
   i = i + 12;
end

Анимация движения маятника в Scilab. Рисуется каждая 12 точка — это имитация sleep()

Под действием выбранного управления, маятник быстренько стабилизируется и не бултыхается безумно:

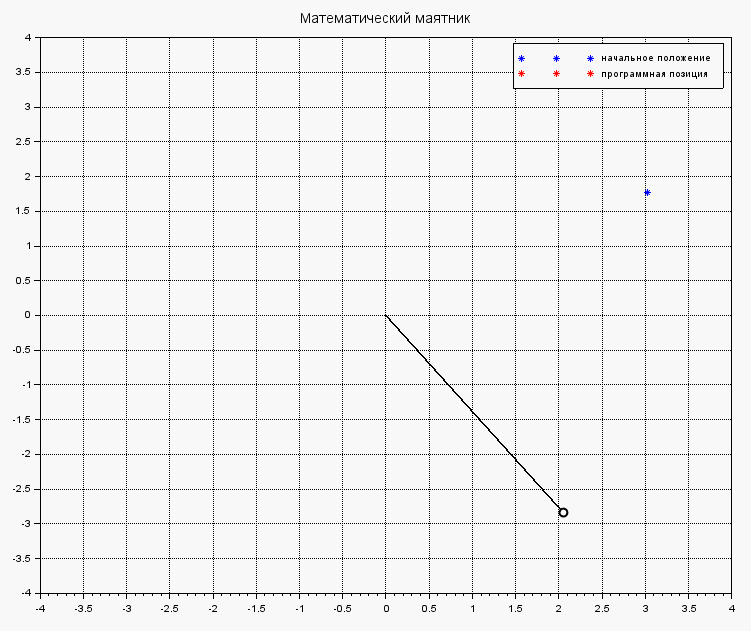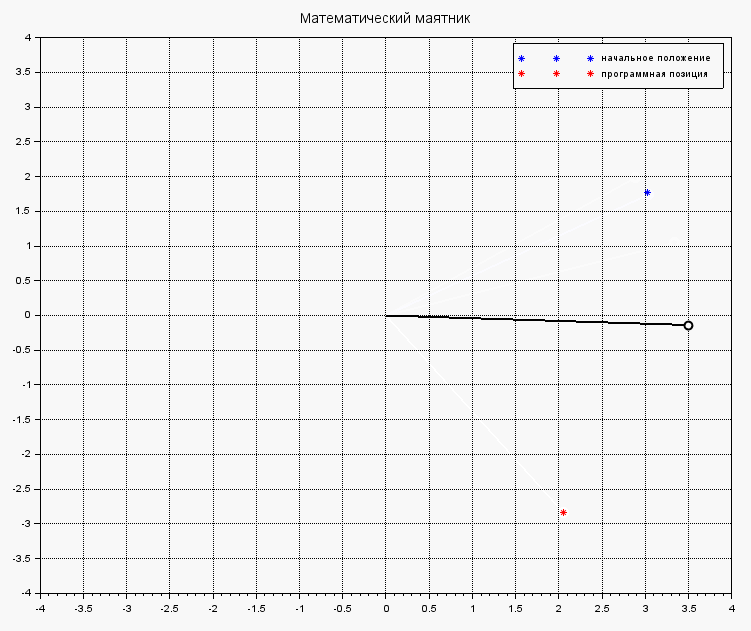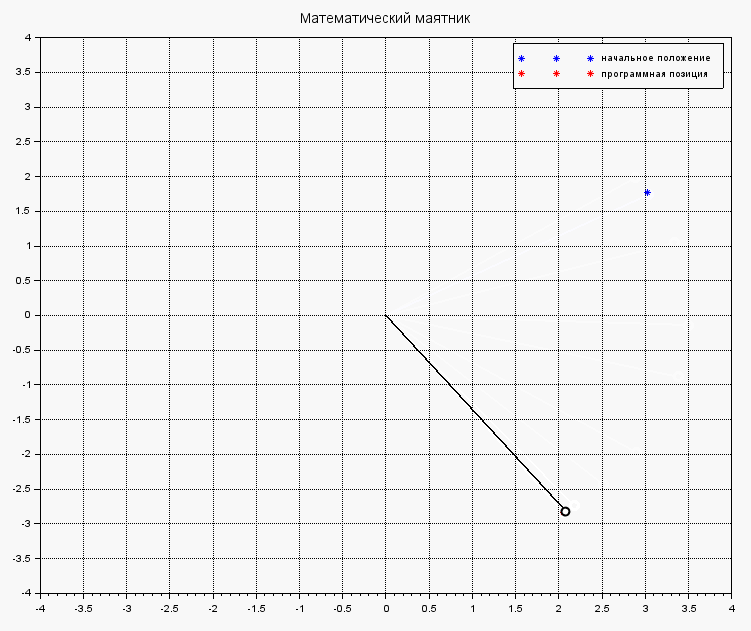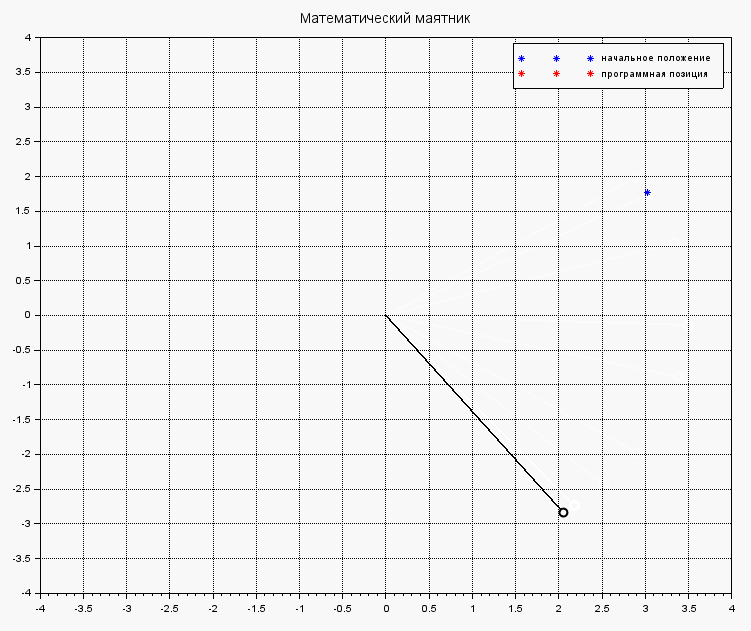
Стабилизация маятника с управлением

Если же в теле функции systNelin() исключить найденное управление из процеса стабилизации маятника, получим поведения объекта под действием на него исходных внешних сил:

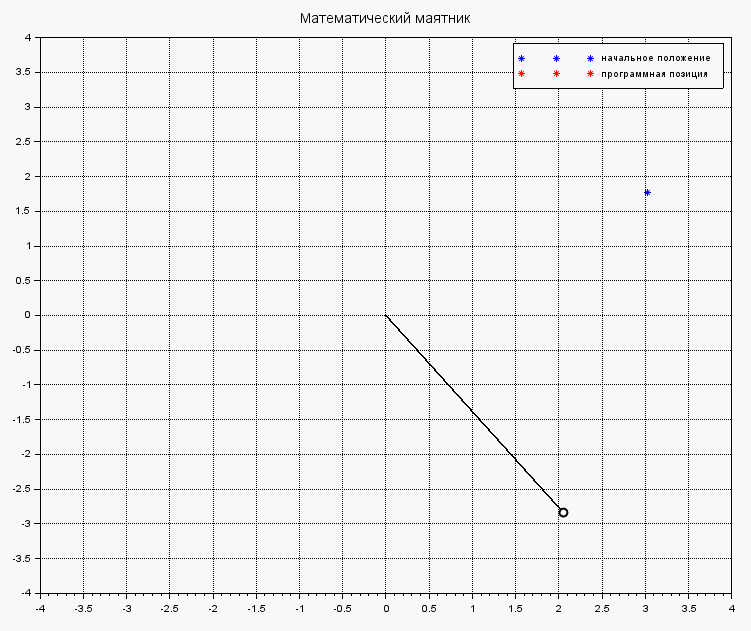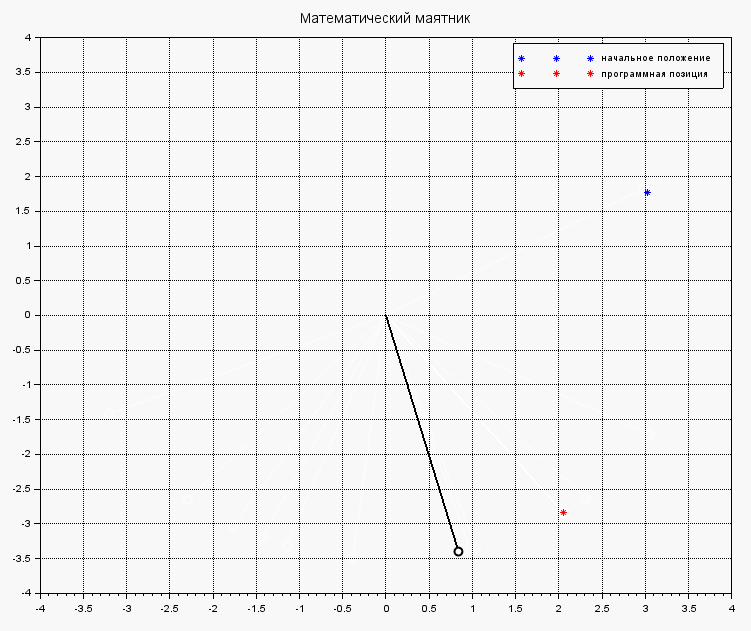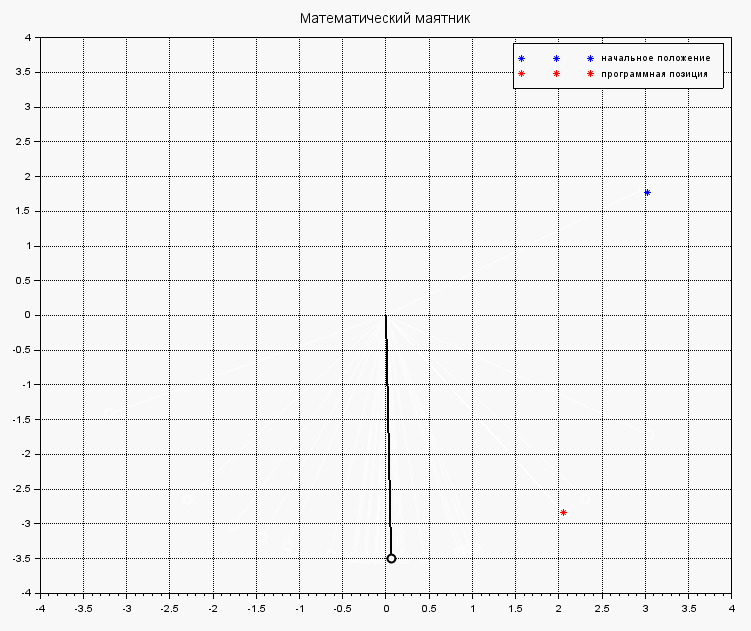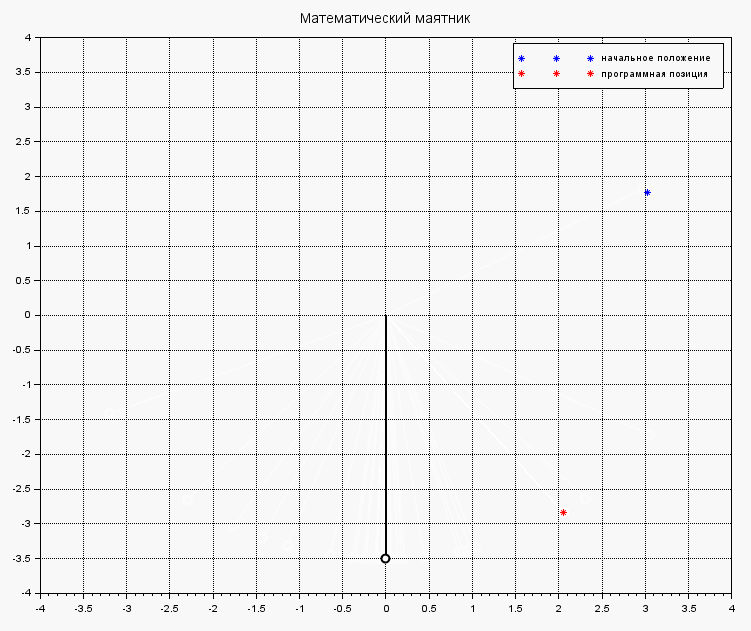
Стандартное поведение маятника

Нравится
109
(лайкай без регистрации)

Библиографическое описание:

Медведев, К. С. Поиск допустимого управления в задаче стабилизации / К. С. Медведев, Р. И. Голубев. — Текст : непосредственный // Молодой ученый. — 2016. — № 12 (116). — С. 38-42. — URL: https://moluch.ru/archive/116/31765/ (дата обращения: 26.05.2023).



В данной работе приведен алгоритм построения стабилизирующего управления для системы дифференциальных уравнений с запаздыванием в управлении и найден критерий существования такого управления.

Ключевые слова: управление, запаздывание, дифференциальные уравнения с запаздыванием, устойчивость

Дифференциальные уравнения с запаздыванием в управлении возникают при решении различных экономических и технических задач. В данной работе рассматривается линейная система с запаздыванием в управлении. Основной целью работы является построение стабилизирующего управления и нахождение критериев его существования.

Задача построения стабилизирующего управления.

Рассмотрим линейную систему с запаздыванием в управлении:

(1)

где ℎ > 0 — запаздывание, матрицы. Предположим также, что пара матриц — полностью управляема. Требуется выбрать управление таким образом, чтобы замкнутая система оказалась асимптотически устойчивой. В [1] было предложено выбирать управление в виде

В момент , когда определяется управление, значение ещё неизвестно. Из (1) получим, что

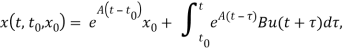
(2)

Построенное таким образом управление (2) является хорошим, поскольку зависит только от и от значений на интервале , т. е. не требует от нас знания будущих состояний системы.

Проверим, что замкнутая система (1)–(2) устойчива, то есть все корни её характеристического уравнения имеют отрицательные вещественные части. Для этого умножим

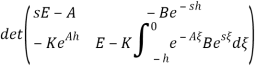
на

и в результате получим

В силу сделанного предположения о полной управляемости пары матриц найдётся стабилизирующее систему управление. Следует отметить, что выбранное управления обеспечивает конечный спектр замкнутой системы (1)–(2), несмотря на наличие запаздывания в системе (1).

Непосредственное использование управления (2) затруднено необходимостью вычисления интеграла

Продифференцировав данное соотношение, получим дифференциальное уравнение, решение которого позволяет находить Однако, как было замечено в [1], это приводит к появлению в системе дополнительного уравнения для 𝑧(𝑡), которое в отдельности является неустойчивым (если исходная система неустойчива). Более того, полученная таким образом система

оказывается неустойчивой даже для стабилизирующего управления. В самом деле, умножив характеристическую матрицу

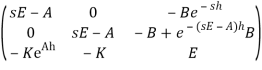
последовательно на

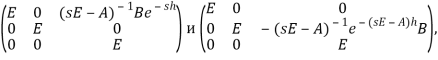
получим

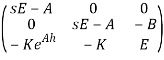
откуда характеристическая функция имеет вид

Поэтому, в [1] было рекомендовано аппроксимировать интеграл квадратурной формулой:

(3)

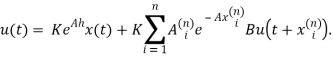
Таким образом получим новую замкнутую систему (1)–(3). Можно проверить, что её спектр, в отличии от исходной системы, бесконечен. Для некоторых значениях параметров устойчивость системы (1)–(3) не достигается ни при каком количестве узлов 𝑛.

Поиск допустимых значений коэффициента ввыражении для стабилизирующего управления.

Далее для простоты расчетов будем рассматривать скалярный случай, то есть , , . Для устойчивости системы (1)–(2) необходимо, чтобы уравнение внутренней динамики управления:

(4)

оказалось устойчивым. Это означает, что уравнение

имеет только такие решения , что , где Re(s) -вещественная часть комплексного числа s. С учётом того, что

если , то для устойчивости (4) достаточно, чтобы было выполнено следующее условие:

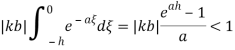
Учитывая вышесказанное, параметр 𝑘 управления (3) будем выбирать из следующих условий:

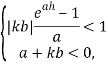
или, что то же самое,

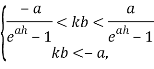
ввиду того, что для всех 𝑎. Так как

то получаем условие

Множество , удовлетворяющих условию, будет непусто, если

или, что то же самое,

Область, соответствующая допустим значениям , приведена на рис. 1.

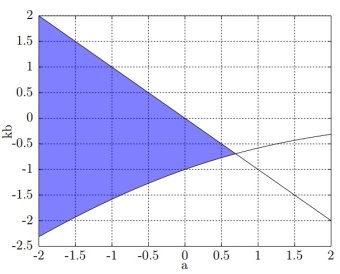
Рис. 1: Возможные значения kb для h=1

Заключение.

В данной работе предложен алгоритм построения стабилизирующего управления на основе метода компенсации запаздывания. Кроме того был найден критерий существования стабилизирующего управления для случая когда матричные коэффициенты являются скалярами. Очевидно, что для скалярного случая существование стабилизирующего управления не зависит от величины b.

Литература:

1. Manitius A., Olbrot A. W. Finite spectrum assignment problem for systems with delays // Automatic Control, IEEE Transactions on, 1979. № 24(4). P. 541–552.
2. Michiels W., S. Mondi´e, D. Roose. Finite Spectrum Assignment of Unstable Time-Delay Systems With a Safe Implementation// Automatic Control, IEEE Transactions on, 2003. № 12. P. 2207–2212