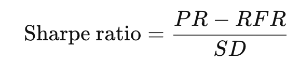Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.
Что такое стандартное отклонение портфеля?
Стандартное отклонение портфеля относится к волатильности портфеля, которая рассчитывается на основе трех важных факторов, включая стандартное отклонение каждого из активов, присутствующих в общем портфеле, соответствующий вес этого отдельного актива в общем портфеле и корреляцию. между каждой парой активов портфеля.
Оглавление
- Что такое стандартное отклонение портфеля?
- Интерпретация стандартного отклонения портфеля
- Пример
- Как рассчитать стандартное отклонение портфеля?
- Формула стандартного отклонения портфеля
- Расчет стандартного отклонения портфеля из трех активов
- Видео о стандартном отклонении портфеля
- Заключение
- Рекомендуемые статьи
Интерпретация стандартного отклонения портфеля
Это помогает определить риск инвестиций по отношению к ожидаемому доходу.
- Стандартное отклонение портфеля рассчитывается на основе стандартного отклонения доходности каждого актива в портфеле, доли каждого актива в общем портфеле, т. е. их соответствующих весов в общем портфеле, а также корреляции между каждой парой активов в портфеле. портфолио.
- Высокое стандартное отклонение портфеля подчеркивает, что риск портфеля высок, а доход более изменчив и, следовательно, нестабилен.
- Портфель с низким стандартным отклонением предполагает меньшую волатильность и большую стабильность доходности портфеля и является очень полезным финансовым показателем при сравнении различных портфелей.
Пример
Раман планирует ежемесячно инвестировать определенную сумму денег в один из двух фондов, которые он выбрал для инвестиционных целей.
Детали которого воспроизведены ниже:
- Предполагая, что стабильность доходности наиболее важна для Рамана при осуществлении этих инвестиций и сохранении других факторов постоянными, мы легко можем увидеть, что оба фонда имеют среднюю норму доходности 12%; однако фонд А имеет стандартное отклонение, равное 8, что означает, что его средняя доходность может варьироваться от 4% до 20% (путем прибавления и вычитания восьми из средней доходности).
- С другой стороны, фонд B имеет стандартное отклонение 14, что означает, что его доход может варьироваться от -2% до 26% (путем прибавления и вычитания 14 из среднего дохода).
Таким образом, на основе его аппетита к рискуАппетит к рискуАппетит к риску относится к сумме, ставке или проценту риска, который физическое лицо или организация (как определено Советом директоров или руководством) готовы принять в обмен на свой план, цели и инновации. .читать дальше, если Раман хочет избежать избыточной волатильности, он предпочтет инвестировать в фонд А, а не в фонд Б, поскольку он предлагает ту же среднюю доходность с меньшей волатильностью и большей стабильностью доходности.
СведенияФонд АФонд BСредняя норма доходности за последние 3 года12%12%Стандартное отклонение814
Стандартное отклонение портфеля важно, поскольку оно помогает анализировать вклад отдельного актива в портфель. На стандартное отклонение влияет корреляция с другими активами в портфеле и его доля веса в портфеле.
Как рассчитать стандартное отклонение портфеля?
Расчет стандартного отклонения портфеля представляет собой многоэтапный процесс и включает в себя описанный ниже процесс.
Формула стандартного отклонения портфеля
Предполагая, что портфель состоит только из двух активов, стандартное отклонение портфеля с двумя активами можно рассчитать, используя формулу стандартного отклонения портфеля:
- Найдите стандартное отклонение каждого актива в портфеле
- Найдите вес каждого актива в общем портфеле
- Найдите корреляцию между активами в портфеле (в приведенном выше случае между двумя активами в портфеле). Корреляция может варьироваться в диапазоне от -1 до 1.
- Примените значения в тех, которые упомянуты выше, чтобы получить формулу стандартного отклонения. Формула стандартного отклонения. в среднем), интерпретируя таким образом надежность данных. Подробнее о портфеле двух активов.
Давайте разберемся с расчетом стандартного отклонения портфеля для портфеля из трех активов на примере:
Расчет стандартного отклонения портфеля из трех активов
1) – Flame International рассматривает возможность создания портфеля, состоящего из трех акций, а именно: акции A, акции B и акции C.
Краткие сведения приведены ниже:
ПодробностиВес Возраст в портфелеОжидаемая доходность Среднеквадратичное отклонениеАкции A55%8%24%Акции B25%4%18%Акции C20%3%15%
2) – Корреляция между доходностью этих акций выглядит следующим образом:
3) – Для портфеля из трех активов это вычисляется следующим образом:
- Где wA, wB и wC — веса акций A, B и C соответственно в портфеле.
- Где kA, s kB, s kC — стандартное отклонение акций A, B и C соответственно в портфеле.
- Где R(kA, kB), R(kA, kC) и R(kB, kC) — это корреляция между акциями A и B, Stock A и C, B и C соответственно.
- Стандартное отклонение портфеля: 18%
- Таким образом, мы видим, что стандартное отклонение портфеля составляет 18 %, несмотря на то, что отдельные активы в портфеле имеют разные стандартные отклонения (акции A: 24 %, акции B: 18 % и акции C: 15 %) из-за корреляции между активов в портфеле.
Видео о стандартном отклонении портфеля
Заключение
Стандартное отклонение портфеля — это стандартное отклонение нормы доходности инвестиционного портфеля, которое используется для измерения присущей волатильности инвестиций. Он измеряет риск инвестиций и помогает анализировать стабильность доходности портфеля.
Стандартное отклонение портфеля — важный инструмент, который помогает сопоставить уровень риска портфеля с склонностью клиента к риску. Он измеряет общий риск в портфеле, включающий как систематический риск, так и несистематический риск. Большее стандартное отклонение подразумевает большую волатильность и большую дисперсию. Дисперсия В статистике дисперсия (или спред) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Читать далее в доходности и, таким образом, более рискованно. Он помогает измерить постоянство получения доходов и является хорошей мерой для анализа эффективности взаимных фондов и хедж-фондов. Он поддерживает различные активы, обеспечивающие высокую доходность в обмен на более высокий риск благодаря множеству методов управления рисками и хеджирования. Подробнее о стабильной доходности.
Однако уместно отметить, что стандартное отклонение основано на исторических данных, и прошлые результаты могут предсказывать будущие результаты. Тем не менее, они также могут меняться со временем и, следовательно, могут изменить стандартное отклонение, поэтому следует быть более осторожным, прежде чем принимать инвестиционное решение на их основе.
Рекомендуемые статьи
Это было руководство по стандартному отклонению портфеля и его интерпретации с примерами. Также мы научимся рассчитывать стандартное отклонение портфеля (три актива). Вы можете узнать больше об управлении активами из следующих статей:
- Образец формулы стандартного отклонения
- Формула относительного стандартного отклонения
- Карьера в управлении портфелем
- КОРРЕЛ Функция Excel
- 10 лучших книг по управлению капиталом
Время на прочтение
4 мин
Количество просмотров 10K
Изображение: Unsplash
Многие начинающие инвесторы оценивают эффективность собранного ими портфеля активов исключительно на основе полученной прибыли. Это не совсем верно, ведь такой подход совсем не учитывает риск, который сопутствовал получению дохода.
Сегодня мы поговорим о нескольких подходах к оценке результативности инвестиционного портфеля.
Коэффициент Трейнора
Это составная мера эффективности портфеля, которая включает и риск. При этом автор формулы предположил, что существует два компонента риска: риск, порожденный флуктуациями на рынке, и риск, который возникает вследствие колебаний конкретного актива.
Коэффициент Трейнора еще называют коэффициентом вознаграждения к волатильности – он является показателем доходности, которая превышает доходность, которая могла бы быть получена по безрисковым инвестициям, на каждую единицу рынка. Важный момент: при расчете коэффициента доходность соотносится только с систематическим риском, а не с общим.
То есть, чем выше коэффициент Трейнора, тем более эффективен инвестиционный портфель. Рассчитывается этот коэффициент так:
где:
ri=доходность портфеля
rf=безрисковая процентная ставка
β=бета (коэффициент риска)
Портал Investopedia приводит пример использования коэффициента Трейнора в реальных инвестициях. Можно предположить, что десятилетняя доходность индекса S&P 500 (рыночный портфель) составляет 10% годовых, а средний годовой доход от казначейских бондов США (как замена безрисковой процентной ставки) составляет 5%. Также, предположим, что есть три управляющих портфелями, которые показали следующие 10-летние результаты
Коэффициент Трейнора для каждого из них будет таким:
Чем выше коэффициент, тем эффективнее портфель. Таким образом, если основываться только на доходности, то менеджер B кажется наиболее результативным. Но если оценивать связанные с его деятельностью риски, то окажется, что на самом деле лучший результат показал управляющий B.
Коэффициент Шарпа
Эта мера очень похожа на коэффициент Трейнора, но здесь риск – это стандартное отклонение портфеля, а не систематический риск, представленный бетой.
Формула для расчета коэффициента Шарпа выглядит так:
, где
PR=доходность портфеля
RFR=безрисковая процентная ставка
SD=стандартное отклонение
Используя пример из предыдущего раздела, у индекса S&P 500 стандартное отклонение находится на уровне 18% за десятилетний период. Тогда для управляющих портфелями коэффициент Шарпа будет выглядеть так:
Как и в предыдущем случае, оказывается, что лучший портфель не обязательно тот, что приносит наибольшее количество денег. Напротив, наилучший результат – это доходность в совокупности с приемлемым риском.
В отличие от коэффициента Трейнора, коэффициент Шарпа оценивает результативность с учетом диверсификации. Таким образом, эта мера лучше подходит для оценки хорошо диверсифицированных инвестпортфелей.
Коэффициент Йенсена
Эта мера рассчитывается с помощью модели CAPM (Capital Asset Pricing Model), по-русски ее еще называют моделью оценки долгосрочных активов. Ее суть в том, что величина требуемой доходности на вложенные средства определяется не столько специфическим риском актива, а общим уровнем риска всего рынка в целом.
Коэффициент Йенсена в итоге подсчитывает избыточную доходность, которую портфель приносит с превышением ожидаемой доходности. Эта мера доходности называется альфой.
Говоря проще, коффициент Йенсена измеряет, насколько доходность портфеля связана со способностью управляющего портфелем генерировать результаты выше среднего по рынку, с учетом риска. Чем выше коэффициент, тем лучше доходность с учетом риска. Портфолио с последовательно положительным превышающим ожидания доходом будет иметь положительную альфу, и наоборот.
Формула расчета выглядит так:
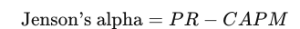
Где
PR=доходность портфеля
CAPM=безрисковая процентная ставка + β(доходность рыночной безрисковой процентной ставки)
Если предположить, что безрисковая процентная ставка находится на уровне 5% и рыночная доходность на уровне 10%, какова будет альфа следующих портфелей?
Подсчет ожидаемой доходности портфелей выглядит так:
Подсчет альфы происходит посредством вычитания ожидаемого дохода из реальной доходности:
Какой же портфель и его управляющий показал лучшие результаты? Управляющий Е оказался лучше всех, поскольку, хоть менеджер F показал такой же уровень доходности, ожидаемая доходность в случае Е была ниже, а бета портфеля была значительно ниже, чем в случае портфеля F.
Важный момент: оценка доходности и риска для акций и портфелей будет меняться со временем. Коэффициент Йенсена требует использование различных безрисковых ставок для каждого интервала. То есть для оценки производительности на пятилетнем отрезке с использованием годовых интервалов, потребуется еще и изучить годовую доходность за вычетом безрискового дохода для каждого года и соотнести ее с годовой доходностью рыночного портфеля минус та же безрисковая ставка.
Полезные ссылки по теме инвестиций и биржевой торговли:
- Открыть брокерский счет онлайн
- Тестовый счет с виртуальными деньгами
- Софт для торговли на бирже: торговый терминал, мобильные приложения
- Структурные продукты
- Модельные портфели
Читайте обзоры, аналитику рынков и инвестидеи в Telegram-канале ITI Capital
Download Article
Download Article
The standard deviation of a portfolio represents the variability of the returns of a portfolio.[1]
To calculate it, you need some information about your portfolio as a whole, and each security within it.
Steps
-
1
Calculate the standard deviation of each security in the portfolio. First we need to calculate the standard deviation of each security in the portfolio. You can use a calculator or the Excel function to calculate that.[2]
- Let’s say there are 2 securities in the portfolio whose standard deviations are 10% and 15%.
-
2
Determine the weights of securities in the portfolio. We need to know the weights of each security in the portfolio.
- Let’s say we’ve invested $1000 in our portfolio of which $750 is in security 1 and $250 is in security 2.
- So the weight of security 1 in portfolio is 75% (750/1000) and the weight of security 2 in portfolio is 25% (250/1000).
Advertisement
-
3
Find the correlation between two securities. Correlation can be defined as the statistical measure of how two securities move with respect to each other.[3]
- Its value lies between -1 and 1.
- -1 implies that the two securities move exactly opposite to each other and 1 implies that they move in exactly the same way in same direction.
- 0 implies that there is no relation as of how the securities move with respect to each other.
- For our example, let’s take correlation as 0.25 which means that if one security increases by $1, the other increases by $0.25.
-
4
Calculate the variance. Variance is the square of standard deviation.[4]
- For this example, variance would be calculated as (0.75^2)*(0.1^2) + (0.25^2)*(0.15^2) + 2*0.75*0.25*0.1*0.15*0.25 = 0.008438.
-
5
Calculate standard deviation. Standard deviation would be square root of variance.[5]
- So, it would be equal to 0.008438^0.5 = 0.09185 = 9.185%.
-
6
Interpret the standard deviation. As we can see that standard deviation is equal to 9.185% which is less than the 10% and 15% of the securities, it is because of the correlation factor:
- If correlation equals 1, standard deviation would have been 11.25%.
- If correlation equals 0, standard deviation would have been 8.38%.
- If correlation equals -1, standard deviation would have been 3.75%.
Advertisement
Add New Question
-
Question
How and why would I diversify a portfolio?
Diversify by investing in many different kinds of assets at the same time: stocks, bonds, and commodities, as well as mutual funds and exchange-traded funds that invest in those assets. Do this because these various assets will appreciate in value at different rates, thus protecting you by offsetting temporary losses in one asset class with simultaneous gains in another.
-
Question
Why is a standard deviation of portfolio important?
It is important to people who are interested in stability of income. It allows comparison of the stability of one investment to that of another.
-
Question
Which portfolio(s) is/are good to create?
That depends on your goals and your tolerance for risk. If your desire for capital appreciation outweighs your fear of losing any money, you’ll accumulate an aggressive portfolio of «growth» stocks. If you’re more interested in safety than impressive gains, you’ll buy blue-chip stocks and index funds. Discuss this with a fee-only advisor.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 121,105 times.
Did this article help you?
Прежде чем составить хороший долгосрочный инвестиционный портфель, инвесторам стоит сравнить разные комбинации активов на основе исторических данных (провести бэктестинг портфеля, например, с помощью нашего конструктора). Результаты бэктестинга не могут гарантировать будущий результат, но они дают полезную информацию о выбранном распределении активов с помощью трех финансовых коэффициентов — Шарпа, Сортино и вариации. Рассказываем, как их правильно читать и использовать.
Что вы узнаете из статьи
- Чем выше коэффициенты Шарпа и Сортино, тем больше доходности получает инвестор на единицу риска.
- Чем ниже коэффициент вариации, тем более сбалансирован портфель по отношению к его волатильности.
- Если коэффициенты Шарпа и Сортино ниже единицы или коэффициент вариации выше единицы, значит портфель недостаточно диверсифицирован.
1. Коэффициент Шарпа — самый популярный индикатор эффективности портфеля
Коэффициент Шарпа был разработан лауреатом Нобелевской премии Уильямом Ф. Шарпом, чтобы помочь инвесторам соотнести доходность инвестиций с риском, который они на себя берут.
Формула для расчета коэффициента Шарпа

Что значит. Коэффициент показывает, какую доходность получает инвестор на одну единицу риска. Чем больше значение, тем лучше риск-скорректированная доходность.
Как читать. Коэффициент Шарпа выше 1 обычно считается «хорошим», так как предполагает, что портфель имеет избыточную доходность (премия выше риска) по сравнению с его волатильностью. В качестве ориентира можно пользоваться следующими значениями:
- показатель от 0 до 1 считается недостаточным — портфель приносит минимальную доходность при заданном риске;
- показатель выше 1 считается хорошим;
- показатель выше 2 считается отличным.
2. Коэффициент Сортино — «улучшенный» коэффициент Шарпа
При расчете волатильности учитывается как рост стоимости портфеля (восходящие движения), так и его снижение (нисходящие движения). . При этом инвестора, как правило, больше беспокоят возможные просадки (то есть отрицательная динамика доходности). Чтобы проанализировать только нисходящую волатильность, на базе коэффициента Шарпа был разработан новый показатель, который сегодня известен как коэффициент Сортино.
Формула для расчета коэффициента Сортино
Что значит. Коэффициент показывает, какую доходность получает инвестор на одну единицу риска падения. Чем больше значение, тем лучше риск-скорректированная доходность.
Как читать. Коэффициент Сортино выше 1 обычно считается «хорошим», так как предполагает, что портфель имеет избыточную доходность по сравнению с его отрицательной волатильностью. В качестве ориентира можно пользоваться теми же нормативными значениями:
- показатель от 0 до 1 считается недостаточным;
- показатель выше 1 считается хорошим;
- показатель выше 2 считается отличным.
3. Коэффициент вариации — баланс риска и доходности портфеля
Ещё один способ сопоставить риск и доходность инвестиционного портфеля — рассчитать коэффициент вариации. Для этого потребуются лишь два показателя — среднегодовая волатильность (стандартное отклонение доходностей) и среднегодовая доходность инвестиционного портфеля. Всё просто: чтобы получить коэффициент нужно поделить одно число на другое.
Формула для расчета коэффициента вариации

Что значит. Инвестор, как правило, заинтересован в том, чтобы найти наиболее оптимальное соотношение риска и доходности — и рассматриваемый показатель может в этом помочь. Чем ниже коэффициент вариации, тем более сбалансирован портфель по отношению к его волатильности. То есть при коэффициенте близком к 0 инвестор получает избыточную доходность, тогда как при коэффициенте вариации 1 и выше — риски неоправданно высоки. Если же коэффициент показывает отрицательное значение — это означает, что портфель генерировал убыток на рассматриваемом периоде.
Как читать. «Хороший» коэффициент вариации близок к 0, но не отрицателен. Можно придерживаться таких правил:
- равен 1 и выше — портфель очень волатилен, его можно улучшить;
- значение меньше 1, но не ниже 0 — это хорошо, портфель сбалансирован.
Что делать, если у портфеля плохие коэффициенты
В сбалансированном портфеле все три коэффициента должны иметь хорошие значения. Если это не так, значит вложения не достаточно диверсифицированы. Портфель можно улучшить, если, например:
- немного изменить соотношение по классам активов (облигации, акции, золото, инструменты денежного рынка);
- увеличить и уменьшить доли некоторых стран или секторов,
- добавить фонды, активы которых номинированы в разных валютах.
В конструкторе есть функция сравнения портфелей, с ее помощью можно посмотреть, как меняются коэффициенты и доходность при внесении изменений в портфель.
Вывод
Коэффициенты Шарпа, Сортино и вариации — важные показатели, которыми можно руководствоваться при выборе активов в свой инвестиционный портфель. Все эти показатели доступны в нашем конструкторе при тестировании на историческом периоде портфелей из FinEx ETF. Полезно использовать одновременно все три коэффициента, не отдавая предпочтение лишь одному из них.
Что ещё почитать по теме: