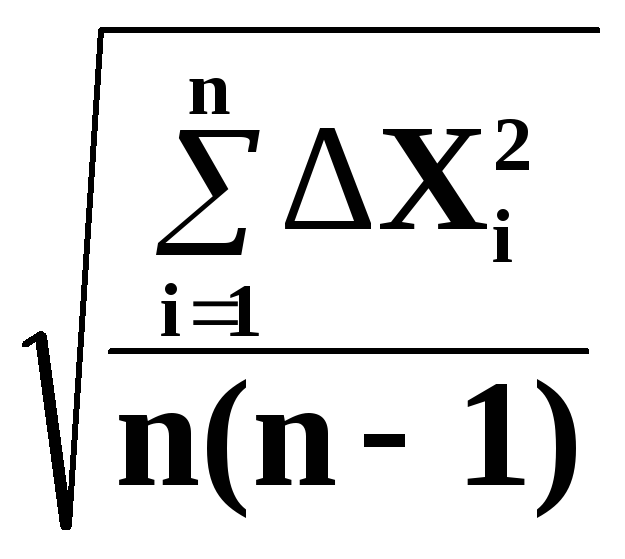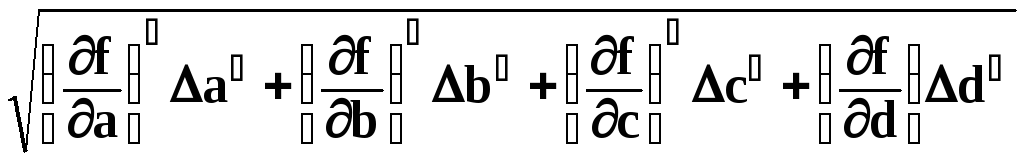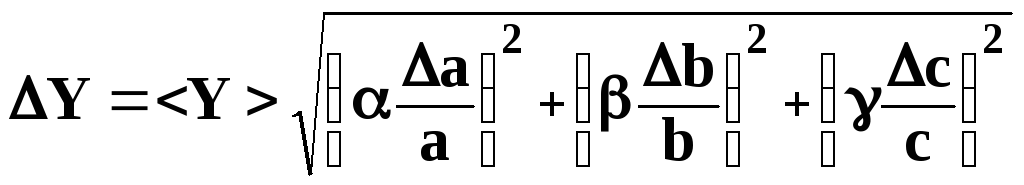Загрузить PDF
Загрузить PDF
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
-
1
Запишите числовые значения, которые вы собираетесь анализировать. Мы проанализируем случайно подобранные числовые значения в качестве примера.
- Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.
Реклама
-
1
Для того чтобы посчитать среднее значение, нужно сложить все имеющиеся числовые значения и разделить получившееся число на их количество.
- Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
- То есть, в нашем случае μ равно (12+55+74+79+90)/5 = 62.
-
1
Мы будем считать среднее отклонение. Среднее отклонение = σ = квадратный корень из [(Σ((X-μ)^2))/(N)].
- Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
Реклама
-
1
Считаем среднюю погрешность (среднего значения). Это оценка того, насколько сильно округляется общее среднее значение. Чем больше числовых значений, тем меньше средняя погрешность, тем точнее среднее значение. Для расчета погрешности надо разделить среднее отклонение на корень квадратный от N. Стандартная погрешность = σ/кв.корень(n).
- Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.
Советы
- Расчеты среднего значения, среднего отклонения и погрешности годятся для анализа равномерно распределенных данных. Среднее отклонение математического среднего значения распределения относится приблизительно к 68% данных, 2 средних отклонения – к 95% данных, а 3 – к 99.7% данных. Стандартная погрешность же уменьшается при увеличении количества значений.
- Простой в использовании калькулятор для расчета среднего отклонения.
Реклама
Предупреждения
- Считайте дважды. Все делают ошибки.
Реклама
Об этой статье
Эту страницу просматривали 66 314 раз.
Была ли эта статья полезной?
3
Расчёт
погрешностей при измерениях физических
величин
При
прямых
измерениях
физических величин (значение величины
определяется непосредственно измерительным
прибором) могут быть допущены три вида
погрешностей (ошибок измерений):
а) систематические (методические
и приборные);
б)
случайные;
в)
грубые (промахи).
Грубые
ошибки
(или промахи) нужно
сразу же исключить
и провести новые измерения.
Систематические
и случайные ошибки
нужно учитывать.
Стандартная
погрешность
измерения величины Х
рассчитывается по формуле:
Х
=
,
(1)
где
Хсист
— стандартная систематическая
погрешность, а Хсл
— стандартная случайная
погрешность.
Методические
систематические
погрешности нужно по возможности
устранить
или учесть
путём
введения специальных поправочных
коэффициентов к измеряемой величине
Х.
Приборные
систематические
погрешности определяются по классу
точности прибора. Существуют семь
классов точности приборов — 0,1; 0,2; 0,5;
1,0; 1,5; 2,5; 4,0.
Е
сли
класс
точности
на шкале прибора заключён
в кружок
(прибор нормирован по относительной
погрешности), например, 0,5 , то
Хсист
=
Хприб
=
0,01.К.Х,
(2а)
где
К
— класс точности прибора, Х
— измеренное значение физической
величины.
Если
класс
точности
на шкале прибора не
заключён в кружок
(прибор нормирован по приведенной
погрешности), то Хсист
=
Хприб
=
0,01.К.Хmax,
(2b)
где
Хmax
-верхний предел измерений прибора.
Если
класс
точности прибора не
известен,
то погрешность
принимают равной половине
цены наименьшего деления
шкалы стрелочного прибора, и одного
наименьшего деления шкалы цифрового
прибора. Если стрелка прибора перемещается
вдоль шкалы скачками,
как например, у ручного секундомера, то
приборную
погрешность
принимают равной цене
деления, соответствующего одному
скачку стрелки.
Для
определения случайной
погрешности
измерения проводят многократно.
За
наиболее достоверное
значение
непосредственно измеряемой физической
величины Х
принимают среднее из всех n
измерений:
<X>=
. (3)
Стандартная
случайная
погрешность
равна:
Хсл
= tn
, (4)
где
Хi
=
|<X>
— Xi|
— абсолютная погрешность i-го
измерения; tn
— коэффициент
Стьюдента,
зависящий от числа
измерений
n
и от требуемой надёжности
получаемого результата, определяемый
по специальной таблице (cм.
ниже). При числе измерений n
5
с надёжностью =2/3
коэффициент Стьюдента tn
= 1.
Относительной
погрешностью измерения величины Х
называется величина:
Х
=
.
(5)
Истинное
значение измеряемой величины Х
с надёжностью
находится в интервале [Х
— Х,
Х
+ Х],
где Х
определяется формулой (3), а Х
— формулой (1) с подстановкой значений
Хсист
и Хсл,
рассчитанных по формулам (2) и (4). Условно
это записывают в виде:
X
= <X>
ΔX
. (6)
При
косвенных
измерениях
значение физической величины определяется
путём
прямых
измерений других физических величин,
а также использования известных
параметров
измерительной установки и справочных
данных
с дальнейшей подстановкой этих значений
в рабочую формулу и соответствующих
расчётов.
Например,
Y
= f (a,b,c,d),
где
a
= a
a,
b = b
b,
c = c
c,
d = d
d.
Наиболее
близким к истинному значению будет:
Y
=f
(a,
b,
c,
d),
(7)
а
стандартная погрешность
Y
принимается равной:
Y=
. (8)
В
простых случаях, когда, например, Y
= a
b
c,
удобно расчёт вести по формуле:
.
(9)
Истинное
значение измеряемой величины Y
находится в интервале [Y
— Y,
Y
+ Y
],
где Y
определяется формулой (7), а Y
— формулой (8) или (9). Таким образом,
результат может быть представлен в
стандартной форме (6):
Y
= <Y>
Y
.
При
записи результата измерений в стандартной
форме необходимо соблюдать
правила
округления:
1-ое
правило
— погрешности Х
или Y
округляются до
двух значащих цифр,
если первая цифра единица, и до
одной значащей цифры
во всех остальных случаях;
2-ое
правило
— средние значения измеряемых величин
Х
или <Y>
округляются
до
последнего десятичного разряда,
который используется при записи
погрешности.
Коэффициенты
Стьюдента
tn
|
n |
|
||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,99 |
|
|
2 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
63,7 |
|
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
9,9 |
|
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
5,8 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
4,6 |
|
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
4,0 |
|
7 |
0,72 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,7 |
|
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,5 |
|
9 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
3,4 |
|
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
3,3 |
|
100 |
0,68 |
0,85 |
1,0 |
1,3 |
1,7 |
2,0 |
2,6 |
|
|
0,67 |
0,84 |
1,0 |
1,3 |
1,6 |
2,0 |
2,6 |
МУ
составлены доц. Петренко Л.Г.
2002-2003 уч.г.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешность и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 1 мин
Два термина, которые студенты часто путают в статистике, — это стандартная ошибка и погрешность .
Стандартная ошибка измеряет точность оценки среднего значения генеральной совокупности. Он рассчитывается как:
Стандартная ошибка = с / √n
куда:
- s: Стандартное отклонение выборки
- n: размер выборки
Погрешность измеряет полуширину доверительного интервала для среднего значения генеральной совокупности.Он рассчитывается как:
Погрешность = z*(s/√n)
куда:
- z: значение Z, соответствующее заданному уровню достоверности
- s: Стандартное отклонение выборки
- n: размер выборки
Давайте рассмотрим пример, иллюстрирующий эту идею.
Пример: допустимая погрешность и стандартная ошибка
Предположим, мы собираем случайную выборку черепах со следующей информацией:
- Размер выборки n = 25
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Теперь предположим, что мы хотим создать 95% доверительный интервал для истинного среднего веса популяции черепах. Формула для расчета этого доверительного интервала выглядит следующим образом:
Доверительный интервал = x +/- z*(s/√n)
куда:
- x : выборочное среднее
- s: Стандартное отклонение выборки
- n: размер выборки
- z: значение Z, соответствующее заданному уровню достоверности
Z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Обратите внимание, что более высокие уровни достоверности соответствуют большим значениям z, что приводит к более широким доверительным интервалам. Это означает, что, например, 99-процентный доверительный интервал будет шире, чем 95-процентный доверительный интервал для того же набора данных.
Стандартная ошибка будет рассчитываться как:
Standard error** = s/√n = 18.5/√25 = **3.7
Погрешность будет рассчитываться как
Margin of error** = z*(s/√n) = 1.96*(18.5/√25) = **7.25
И 95% доверительный интервал будет рассчитываться как
95% Confidence Interval** = x +/- z*(s/√n) = 300 +/- 1.96*(18.5/√25) = **[292.75, 307.25]
Обратите внимание, что ширина всего доверительного интервала составляет 307,25 – 292,75 = 14,5 .
Обратите внимание, что погрешность равна половине этой ширины: 14,5/2 = 7,25 .
Обратите также внимание, что предел погрешности всегда будет больше стандартной ошибки просто потому, что предел погрешности равен стандартной ошибке, умноженной на некоторое критическое значение Z. В предыдущем примере мы умножили стандартную ошибку на 1,96, чтобы получить погрешность.
Дополнительные ресурсы
Что такое доверительные интервалы?
Стандартное отклонение и стандартная ошибка: в чем разница?