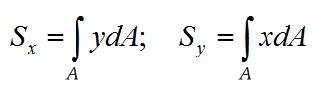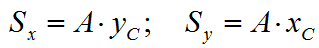В прошлой статье “цикла в цикле” мы разобрали площадь сечения, кратко коснулись её использования для определения напряжений и повторили как с помощью интегрирования определить площадь сложного сечения. В этой статье речь пойдет о статических моментах. И первое, что стоит о них сказать — это то, что, в отличие от площади и размеров сечения, статический момент достаточно абстрактная величина, то есть их нельзя измерить неким прибором, увидеть или ощутить тактильно. Единственный путь определения статического момента — бусидо расчет. Однако для того, чтобы получить ответ на вопрос “сломается ли деталь” при изгибах и кручении, эта величина очень удобна.
Сначала немного теории
Проясним физический смысл величины.
Статические моменты выражают действие момента собственного веса стержня относительно некоторых осей. Впрочем, тут стоит всё же разобраться более подробно:
Представим, что у нас есть стержень какого-то сложного сечения. Мы также произвольно построим систему координат (но желательно всё же, чтобы она проходила близко к сечению нашего стержня). А теперь важный момент: стержень жестко закреплен основанием на осях, которыми мы задались.
На такой стержень действует сила тяжести, вызывая момент. Что это такое мы уже выяснили в части, посвященной изгибу. Для тех, кто заметку про изгиб не читал: момент силы — это произведение силы на плечо (расстояние от точки приложения силы до рассматриваемой точки). Для всего стержня он будет:
g – ускорение свободного падения
ρ – плотность (объёмный вес) материала стержня
l – длина стержня
e – плечо момента. Если стержень “закреплен” на оси, то плечо будет равно расстоянию до этой оси (x или y). е — потому что эксцентриситет!
F – площадь поперечного сечения стержня.
При этом мы можем заметить следующее:
- Плотность материала для любого куска стержня пусть будет одинакова, как и его длина, а значит они вместе с ускорением свободного падения будут константами для моментов каждой точки поперечного сечения стержня и не повлияют на разницу в величине моментов разных точек. По сути, их можно вынести за скобки и рассматривать только произведение площади на расстояние до оси.
- Если расстояние до осей не очень велико по сравнению с размерами сечения, то каждая материальная точка будет иметь свой момент (потому что точки находятся на неодинаковом расстоянии до оси). Это значит, что для определения момента от собственного веса нужно разделить сечение на как можно большее количество элементарных площадок, умножить площадь каждой из них на расстояние до оси и, затем, просуммировать получившиеся произведения.
А сумма произведений предельно малых площадей сечения на расстояние до оси – это интеграл, следовательнодля определения моментов относительно системы координат xOy нам необходимо прежде всего вычислить такие два интеграла:
Каждый из этих интегралов как раз и представляет собой сумму произведений элементарных площадок dF на расстояние до соответствующей оси (x или y).
Элементарная площадка – это кусок сечения с очень малой площадью. Настолько малой, что она меньше всякой возможности её измерить и меньше всякого конечного значения вообще. Но нулю она не равна.
Эти интегралы называются соответственно – статические моменты сечения относительно осей x и y.
Статический момент может быть как положительным, так и отрицательным. Величина статического момента зависит от выбора системы координат. Имеет размерность см3.
Теперь попробуем параллельно перенести оси так, чтобы расстояния между ними были a и b. Теперь x1=x-a, y1=y-b. Изменятся ли статические моменты в таком случае? Если изменятся, то как? И что нам может дать такое изменение расположения осей? Давайте посмотрим:
Значит при переносе осей без их поворота статический момент изменяется на величину, равную произведению площади всего сечения на расстояние между осями.
Можно подобрать оси (а, следовательно и величины a и b) так, что b*F=Sx и a*F=Sy .
В таком случае статический момент сечения относительно осей будет равен нулю. Такие оси будут называться центральными, а начало отсчета такой системы координат – центром тяжести сечения.
Т.е. статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если оно закреплено (опирается) в точке центра тяжести. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение равно нулю.
Тут нам важно одно свойство центра тяжести – если сечение имеет ось симметрии, то центр тяжести всегда лежит на ней. Если осей симметрии целых две, (а они вообще-то должны пересекаться) то точка их пересечения – центр тяжести. Следовательно чтобы найти статический момент сложного сечения, состоящего из нескольких простых, симметричных – нужно найти его центр тяжести из выражений:
х1, y1 и x2, y2 – это координаты центров тяжести простых сечений, входящих в состав сложного.
После преобразования получим формулы для координат центра тяжести:
Далее, нужно непосредственно найти статический момент:
Где, x’ и y’ – оси, относительно которых нужно найти статический момент.
Находим статический момент
Пример:
Найти статический момент сечения неравнополочного уголка 14/9 толщиной 10 мм по ГОСТ 8510-86 без учета скруглений относительно осей, указанных на рисунке:
Определим площади и положение центров тяжести двух частей сечения – прямоугольников 130х10 и 90х10:
Координаты центра тяжести сечения определяем по формулам:
Если перенести ось Х на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 4.58 см.
Если перенести ось Y на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 2.12 см.
Найдем статические моменты сечения:
Подведём итоги
Статический момент — величина, характеризующая положение выбранных осей относительно центра тяжести сечения. Статический момент относительно центра тяжести равен нулю. Посчитать его мы можем как произведение площади сечения на расстояние от центра сечения до выбранной оси, но когда расстояние до оси сравнимо с размерами сечения нужно всё же взять интеграл.
Статический момент, кроме определения центра тяжести, используется для расчётов касательных напряжений, что на практике выливается также в расчеты на скалывание (конструкций из дерева).
На очереди моменты инерции.
Автор: Марк Ершов
Редактор, факт-чекер: Кирилл Овчинников
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 718
Статические моменты и координаты центра тяжести
Вычисление статических моментов и координат центра тяжести кривой
а) Пусть материальная точка массы
отстоит от оси
на расстоянии
. Статическим моментом этой точки относительно оси
называют число
. Статическим моментом системы материальных точек
, расположенных по одну сторону от оси
, массы которых равны
, а расстояния от оси
равны
называют число
Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.
Поэтому если точки расположены на координатной плоскости,
, то
где — статический момент относительно оси
и
— относительно оси
.
б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой или по некоторой области
. Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.
Начнем со случая кривой линии , задаваемой уравнением
, причем предположим, что функция
непрерывна и неотрицательна.
Как обычно, разобьем отрезок на части точками
и обозначим через
и
наименьшее и наибольшее значения функции
на отрезке
, Этому разбиению соответствует разбиение дуги
на части
(рис. 60). Из физических соображений ясно, что статический момент
части
относительно оси абсцисс заключен между
и
, где
—длина этой части,
(напомним, что мы положили линейную плотность дуги равной единице). Таким образом,
. Поэтому
, то есть
Так как на отрезке выполняется неравенство
то в тех же границах, что и , заключен интеграл
. Значит,
(1)
Этот интеграл обозначают также следующим образом: или
.
Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» . Его статический момент равен
. А статический момент всей дуги равен сумме элементарных статических моментов, т. е.
. Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что
(2)
Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.
в) Введем понятие центра тяжести.
Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.
Обозначим через и
расстояния центра тяжести кривой от осей ординат и абсцисс.
Тогда, пользуясь определением центра тяжести кривой, получим:
Разрешая полученные равенства относительно и
, найдем координаты центра тяжести плоской кривой
Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.
Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.
Пример 1. Найти статический момент полуокружности относительно диаметра.
Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой
, где
— дифференциал дуги кривой
.
В выбранной системе координат уравнение полуокружности запишется так: . Тогда
и потому
.
Следовательно,
Пример 2. Найдем центр тяжести четверти окружности , расположенной в первом квадранте.
Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому . Достаточно найти только
.
Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:
Отсюда находим, что и
Поскольку длина четверти данной окружности равна
, то
Вычисление статических моментов и координат центров тяжести плоских фигур
Найдем статический момент прямоугольника со сторонами и
относительно стороны
. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны
и
(рис. 61). Масса элементарного прямоугольника равна его площади
(напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен
, а статический момент всего прямоугольника равен
(1)
Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой , где
— непрерывная и неотрицательная функция на отрезке
, снизу осью абсцисс, а с боков прямыми
.
Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота
. Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен
, а потому статический момент всей криволинейной трапеции равен
. В случае, когда не выполняется предположение о неотрицательности функции
, эту формулу надо заменить такой:
(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).
Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу , а потому ордината центра тяжести этой трапеции выражается формулой
Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен
, а статический момент всей трапеции выражается формулой
. Следовательно, абсцисса центра тяжести выражается так:
.
Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:
Решение. Так как параметр одной арки циклоиды изменяется от
до
, то
Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды
.
Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой , то центр тяжести лежит на этой прямой и, следовательно,
. Ордината
центра тяжести находится по формуле
.
Так как , то
.
Итак, центр тяжести данной фигуры находится в точке .
Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды .
Решение. Данная фигура расположена симметрично относительно прямой , следовательно, центр тяжести ее находится на этой прямой, и потому
. Найдем
по формуле
.
Площадь данной фигуры была вычислена раньше, она равна
. Следовательно,
Центр тяжести данной фигуры находится в точке .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Статический момент инерции относительно оси
Рассмотрим поперечное сечение стержня площадью F. Проведем через произвольную точку О оси координат x и y. Выделим элемент площади 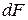
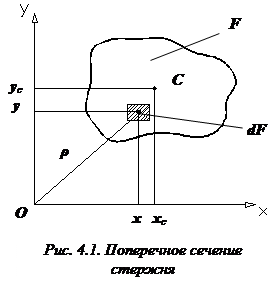
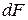
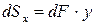
Аналогично статический момент инерции относительно оси y равен:
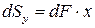
Просуммировав такие произведения по площади F, получим статический момент инерции всей фигуры относительно осей x и y:
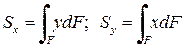
Статический момент инерции фигуры относительно оси измеряется в единицах длины в кубе (см3), и может быть положительным, отрицательным и равным нулю.
Пусть 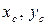

Таким образом, моментом (статическим моментом) площади фигуры относительно оси называется произведение площади на расстояние от ее центра тяжести до оси.
ГЕОМЕТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
ОБЩИЕ
СВЕДЕНИЯ
Как уже известно,
при растяжении и сжатии прочность и
жесткость стержней, напряжения,
возникающие в их поперечных сечениях,
величина потенциальной энергии деформации
и т. д. зависят от площадей поперечных
сечений стержней.
Площадь является
простейшей геометрической характеристикой
поперечного сечения. Если представить
себе сечение состоящим из бесчисленного
множества элементарных
площадок dF
(рис. 1.5), то
площадь всего сечения

При расчетах на
изгиб, кручение, сложное сопротивление,
а также при расчетах сжатых стержней
на устойчивость используются более
сложные геометрические характеристики
сечений: статический момент, а также
осевой (или экваториальный), полярный
и центробежный моменты инерции сечений.
Выражения этих характеристик отличаются
от выражения (1.5) тем, что в них под знаки
интеграла входят произведения элементарных
площадок dF
на функции
координат у,
z,
ρ этих площадок
(см. рис. 1.5). Таким образом, указанные
геометрические характеристики зависят
не только от формы и размеров сечения,
но также от положения осей и точек
(полюсов), относительно которых они
вычисляются.
Геометрические
характеристики сечений простой формы
можно определить по специальным
формулам. Кроме того, в таблицах
нормального сортамента (ГОСТа) приводятся
геометрические характеристики профилей
стандартного проката (уголков, швеллеров,
двутавров). Для определения геометрических
характеристик сложных сечений приходится
расленять их на ряд простых фигур и
пользоваться формулами, устанавливающими
зависимость между геометрическими
характеристиками относительно различных
осей.
Статическим
моментом сечения относительно некоторой
оси
называется
взятая по всей его площади F
сумма произведений элементарных площадок
dF
на их расстояния от этой оси, т.
е.

Статические моменты
выражаются в см3,
m3
и
т. д.
Для сложного
сечения, состоящего из n
частей,
выражения (2.5) можно представить в виде
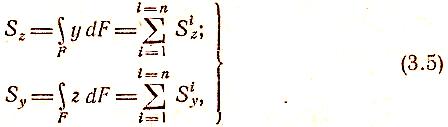
где Siz
и Siy
— статические
моменты i-й
части сечения относительно осей z
и у соответственно.
Итак, статический
момент сложного сечения относительно
некоторой оси равен сумме статических
моментов всех частей этого сечения
относительно той же оси.
Нельзя суммировать
статические моменты частей сечения,
вычисленные относительно различных
осей.
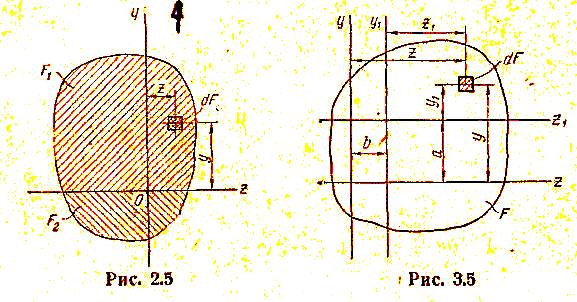
Установим зависимость
между статическими моментами одного и
того же сечения относительно двух
параллельных друг другу осей z
и z1
(рис. 3.5).
Выражения статических моментов
относительно этих осей на основании
(2.5) имеют вид
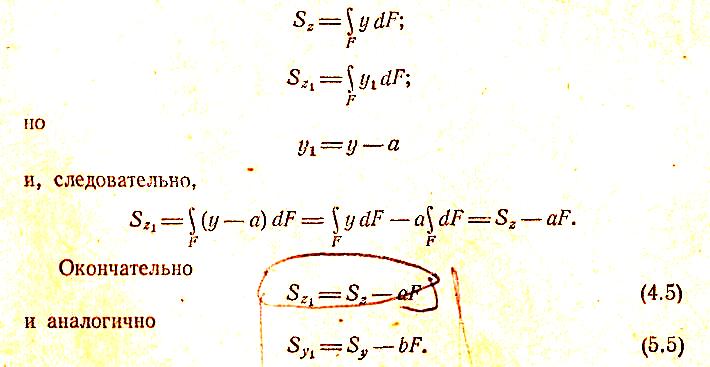
Найдем теперь
положение осей z1
и y1
(рис. 4.5),
относительно которых статические
моменты равны нулю. Для этого приравняем
нулю выражения (4.5)
и (5.5):
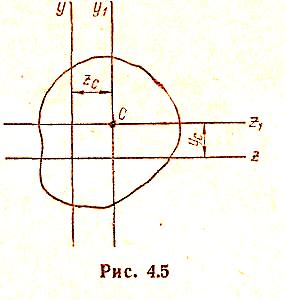
Точка пересечения
таких осей
(точка С на
рис. 4.6) называется
центром тяжести
сечения, а оси
проходящие через центр тяжести, —
центральными
осями. Относительно
любой оси, проходящей через центр тяжести
сечения (т.е. относительно любой
центральной оси), статический момент
равен нулю. Формулы
(6.5) используются для определения
координат центра тяжести сечения.
Для сложного
сечения, установим следующий порядок
определения положения центра тяжести
-
Сложное сечение
разбивается на части, имеющие вид
простых фигур. -
Определяются
площади и положения центров тяжести
каждой фигуры. -
Выбираются
случайные координатные оси у
и z.
4. По формулам (6.5)
вычисляются статические моменты Siv
и Siz
относительно
осей у и
z
каждой фигуры.
Затем путем суммирования значений [в
соответствии с выражениями (3.5)]
определяется статические моменты Sy,
Sz
всего сечения.
5. По формулам (6.5)
вычисляются координаты центра тяжести
всего сечения.
В отдельных случаях,
когда заданное сечение нельзя разбить
на такие фигуры, положения центров
тяжести которых известны, положение
центра тяжести всего сечения необходимо
определять путем непосредственного
интегрирования.
2. Моменты инерции сечений
Осевым (или
экваториальным) моментом инерции сечения
относительно некоторой оси называется
взятая по всей его площади F
сумма произведений элементарных
плош.адок dF
на квадраты, их расстояний от этой оси,
т. е.

Полярным моментом
инерции сечения относительно некоторой
точки (полюса) называется взятая по всей
его площади F
сумма произведений элементарных площадок
dF
на квадраты их расстояний от этой точки,
т. е.

Центробежным
моментом инерции сечения относительно
некоторых двух взаимно перпендикулярных
осей называется взятая по
всей его
площади F
сумма произведений элементарных площадок
dF
на их расстояния от этих осей,
т. е.
Моменты инерции
выражаются в см4,
м4
и т. д.
Осевые и полярные
моменты инерции всегда положительны,
так как в их выражения под знаки интегралов
входят величины площадок dF
(всегда
положительные) и квадраты
расстояний этих площадок от данной оси
или полюса.
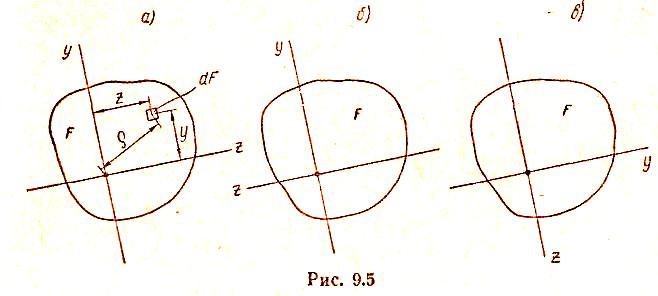
На рис. 9.5,а изображено
сечение площадью F
и показаны оси
у и
z.
Осевые моменты
инерции этого сечения относительно
осей у и z
:
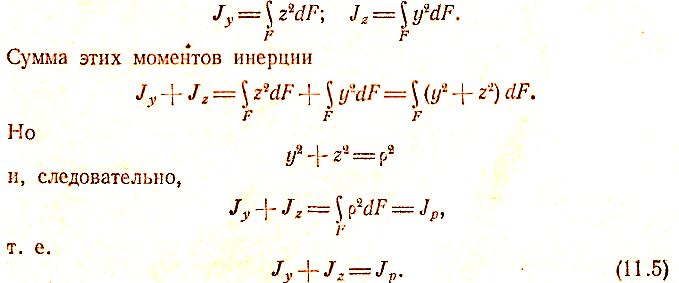
Таким образом,
сумма осевых
моментов инерции сечения- относительно
двух взаимно перпендикулярных осей
равна полярному моменту инерции этого
сечения относительно точки пересечения
указанных осей.
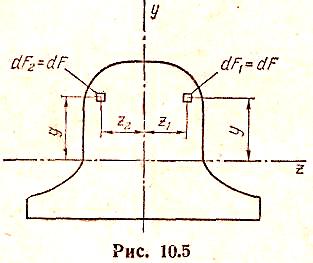
Рассмотрим фигуру,
симметричную относительно одной или
нескольких осей (рис. 10.5). Проведем оси
у и
z
так, чтобы хотя
бы одна из них (в данном случае ось у)
совпадала с
осью симметрии фигуры. Каждой площадке
dF1,
расположенной
справа от оси и,
соответствует
в этом случае такая же площадка dF1
расположенная
симметрично первой, но слева от оси у.
Центробежный
момент инерции каждой пары таких
симметрично расположенных площадок
равен:
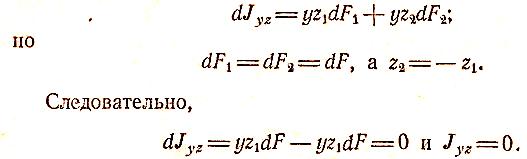
Таким образом,
центробежный
момент инерции сечения относительно
осей, из которых одна или обе совпадают
с его осями симметрии, равен нулю.
Осевой момент
инерции сложного сечения относительно
некоторой оси равен сумме осевых моментов
инерции составляющих его частей
относительно этой же оси.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формулы для расчета геометрической характеристики статического момента сечений, плоских фигур и площади:
Рассмотрим сечение (плоскую фигуру) произвольной формы площадью A:
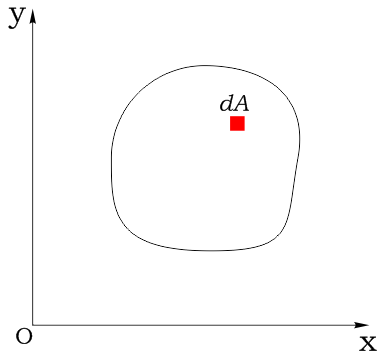
Выделим в нем элементарную площадку dA и зададим систему координат:
Другие видео
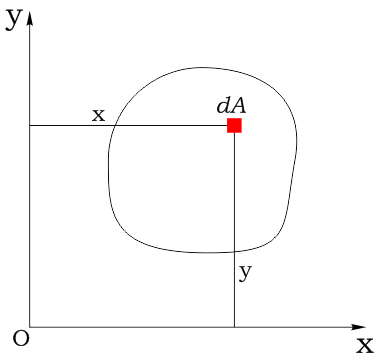
Координаты площадки обозначим соответственно как x и y:
Статический момент элементарной площадки:
Суммируя выражения по всей площади фигуры, получим соответственно:
Единица измерения статического момента [м3].
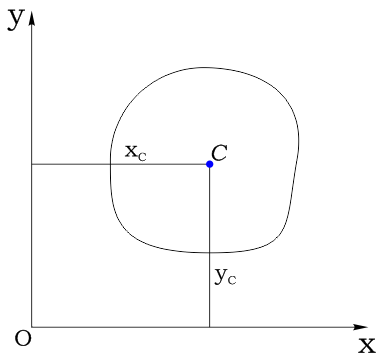
Пусть xC ,yC координаты центра тяжести C фигуры
тогда статические моменты относительно осей x и y:
Положение центра тяжести >
Моменты инерции плоских сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее