Как найти статический момент сечения

В прошлой статье “цикла в цикле” мы разобрали площадь сечения, кратко коснулись её использования для определения напряжений и повторили как с помощью интегрирования определить площадь сложного сечения. В этой статье речь пойдет о статических моментах. И первое, что стоит о них сказать — это то, что, в отличие от площади и размеров сечения, статический момент достаточно абстрактная величина, то есть их нельзя измерить неким прибором, увидеть или ощутить тактильно. Единственный путь определения статического момента — бусидо расчет. Однако для того, чтобы получить ответ на вопрос “сломается ли деталь” при изгибах и кручении, эта величина очень удобна.

Сначала немного теории

Проясним физический смысл величины.
Статические моменты выражают действие момента собственного веса стержня относительно некоторых осей. Впрочем, тут стоит всё же разобраться более подробно:
Представим, что у нас есть стержень какого-то сложного сечения. Мы также произвольно построим систему координат (но желательно всё же, чтобы она проходила близко к сечению нашего стержня). А теперь важный момент: стержень жестко закреплен основанием на осях, которыми мы задались.

На такой стержень действует сила тяжести, вызывая момент. Что это такое мы уже выяснили в части, посвященной изгибу. Для тех, кто заметку про изгиб не читал: момент силы — это произведение силы на плечо (расстояние от точки приложения силы до рассматриваемой точки). Для всего стержня  он будет:

g – ускорение свободного падения

ρ – плотность (объёмный вес) материала стержня

l – длина стержня

e – плечо момента. Если стержень “закреплен” на оси, то плечо будет равно расстоянию до этой оси (x или y). е — потому что эксцентриситет!

F – площадь поперечного сечения стержня.

При этом мы можем заметить следующее:

1. Плотность материала для любого куска стержня пусть будет одинакова, как и его длина, а значит они вместе с ускорением свободного падения будут константами для моментов каждой точки поперечного сечения стержня и не повлияют на разницу в величине моментов разных точек. По сути, их можно вынести за скобки и рассматривать только произведение площади на расстояние до оси.
2. Если расстояние до осей не очень велико по сравнению с размерами сечения, то каждая материальная точка будет иметь свой момент (потому что точки находятся на неодинаковом расстоянии до оси). Это значит, что для определения момента от собственного веса нужно разделить сечение на как можно большее количество элементарных площадок, умножить площадь каждой из них на расстояние до оси и, затем, просуммировать получившиеся произведения. 

А сумма произведений предельно малых площадей сечения на расстояние до оси  – это интеграл, следовательнодля определения моментов относительно системы координат xOy нам необходимо прежде всего вычислить такие два интеграла:

Каждый из этих интегралов как раз и представляет собой сумму произведений элементарных площадок dF на расстояние  до соответствующей оси (x или y). 

Элементарная площадка –  это кусок сечения с очень малой площадью. Настолько малой, что она меньше всякой возможности её измерить и меньше всякого конечного значения вообще. Но нулю она не равна.

Эти интегралы называются соответственно – статические моменты сечения относительно осей x и y. 

Статический момент может быть как положительным, так и отрицательным. Величина статического момента зависит от выбора системы координат.  Имеет размерность см³.
 

Теперь попробуем параллельно перенести оси так, чтобы расстояния между ними были a и b. Теперь x₁=x-a, y₁=y-b. Изменятся ли статические моменты в таком случае? Если изменятся, то как? И что нам может дать такое изменение расположения осей? Давайте посмотрим:

Значит при переносе осей без их поворота статический момент изменяется на величину, равную произведению площади всего сечения на расстояние между осями.

Можно подобрать оси (а, следовательно и величины a и b) так, что b*F=S_x и a*F=S_y .
В таком случае статический момент сечения относительно осей будет равен нулю. Такие оси будут называться центральными, а начало отсчета такой системы координат – центром тяжести сечения.

Т.е. статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если оно закреплено (опирается) в точке центра тяжести. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение равно нулю. 

Тут нам важно одно свойство центра тяжести – если сечение имеет ось симметрии, то центр тяжести всегда лежит на ней. Если осей симметрии целых две, (а они вообще-то должны пересекаться) то точка их пересечения – центр тяжести. Следовательно чтобы найти статический момент сложного сечения, состоящего из нескольких простых, симметричных – нужно найти его центр тяжести из выражений:

х₁, y₁ и x₂, y₂ – это координаты центров тяжести простых сечений, входящих в состав сложного.

После преобразования получим формулы для координат центра тяжести:

Далее, нужно непосредственно найти статический момент:

Где, x^’ и y^’ – оси, относительно которых нужно найти статический момент.

Находим статический момент

Пример:
Найти статический момент сечения неравнополочного уголка 14/9 толщиной 10 мм по ГОСТ 8510-86 без учета скруглений относительно осей, указанных на рисунке:

Определим площади и положение центров тяжести двух частей сечения – прямоугольников 130х10 и 90х10:

Координаты центра тяжести сечения определяем по формулам:

Если перенести ось Х на внешнюю грань уголка, то положение центра тяжести:

По сортаменту положение центра тяжести с учетом закруглений – 4.58 см.

Если перенести ось Y на внешнюю грань уголка, то положение центра тяжести:

По сортаменту положение центра тяжести с учетом закруглений – 2.12 см.

Найдем статические моменты сечения:

Подведём итоги

Статический момент — величина, характеризующая положение выбранных осей относительно центра тяжести сечения. Статический момент относительно центра тяжести равен нулю. Посчитать его мы можем как произведение площади сечения на расстояние от центра сечения до выбранной оси, но когда расстояние до оси сравнимо с размерами сечения нужно всё же взять интеграл.

Статический момент, кроме определения центра тяжести, используется для расчётов касательных напряжений, что на практике выливается также в расчеты на скалывание (конструкций из дерева).

На очереди моменты инерции.

Автор: Марк Ершов
Редактор, факт-чекер: Кирилл Овчинников

Список использованных источников

1. Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
3. Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3

4 734

6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ

Статический момент площади – распространенная на всю площадь сумма произведений элементарных площадок dA на расстояние от них до этой оси Это понятие аналогично моменту силы относительно оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус. Ось центральная – ось, относительно которой статический момент площади равен нулю. Центр тяжести сечения – точка пересечения центральных осей. Если фигура имеет ось симметрии, то эта ось является центральной. Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это следует из свойства определенного интеграла, который можно вычислять по частям – свойство аддитивности (от англ. add – прибавлять, присоединять, складывать). При известных статических Рис. 6.2. Связь знака статического момента площади с его положением в координатной системе моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры: Пример 6.1. Определить положение центральных осей, параллельных основанию и высоте фигуры. Решение Разбиваем сложную фигуру на две простые, в конкретном примере – на два прямоугольника. Их центры тяжести расположены посредине высоты и посредине ширины. Координаты центров тяжести и площади простых фигур Статические моменты площадей простых фигур Координаты центра тяжести составной фигуры Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте. Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.

ГЕОМЕТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ

ОБЩИЕ
СВЕДЕНИЯ

Как уже известно,
при растяжении и сжатии прочность и
жесткость стержней, напряжения,
возникающие в их поперечных сечениях,
величина потенциальной энергии деформации
и т. д. зависят от площадей поперечных
сечений стержней.

Площадь является
простейшей геометрической характеристикой
поперечного сечения. Если представить
себе сечение состоящим из бесчисленного
множества элементарных
площадок dF
(рис. 1.5), то
площадь всего сечения

При расчетах на
изгиб, кручение, сложное сопротивление,
а также при расчетах сжатых стержней
на устойчивость используются более
сложные геометрические характеристики
сечений: статический момент, а также
осевой (или экваториальный), полярный
и центробежный моменты инерции сечений.
Выражения этих характеристик отличаются
от выражения (1.5) тем, что в них под знаки
интеграла входят произведения элементарных
площадок dF
на функции
координат у,
z,
ρ этих площадок
(см. рис. 1.5). Таким образом, указанные
геометрические характеристики зависят
не только от формы и размеров сечения,
но также от положения осей и точек
(полюсов), относительно которых они
вычисляются.

Геометрические
характеристики сечений простой формы
можно определить по специальным
формулам. Кроме того, в таблицах
нормального сортамента (ГОСТа) приводятся
геометрические характеристики профилей
стандартного проката (уголков, швеллеров,
двутавров). Для определения геометрических
характеристик сложных сечений приходится
рас­ленять их на ряд простых фигур и
пользоваться формулами, устанавливающими
зависимость между геометрическими
характеристиками относительно различных
осей.

Статическим
моментом сечения относительно некоторой
оси
называется
взятая по всей его площади F
сумма произведений элементарных площадок
dF
на их расстояния от этой оси, т.
е.

Статические моменты
выражаются в см³,
m³
и
т. д.

Для сложного
сечения, состоящего из n
частей,
выражения (2.5) можно представить в виде

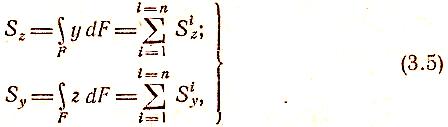
где Sⁱ_z
и Sⁱ_y
— статические
моменты i-й
части сечения относительно осей z
и у соответственно.
Итак, статический
момент сложного сечения относительно
некоторой оси равен сумме статических
моментов всех частей этого сечения
относительно той же оси.

Нельзя суммировать
статические моменты частей сечения,
вычисленные относительно различных
осей.

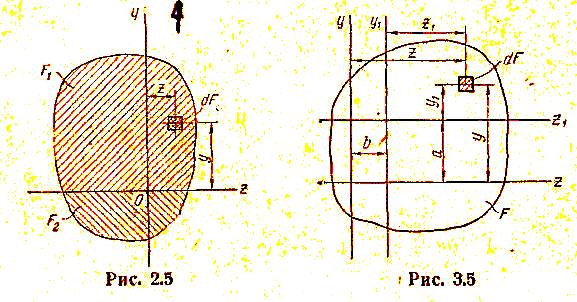
Установим зависимость
между статическими моментами одного и
того же сечения относительно двух
параллельных друг другу осей z
и z₁
(рис. 3.5).
Выражения статических моментов
относительно этих осей на основании
(2.5) имеют вид

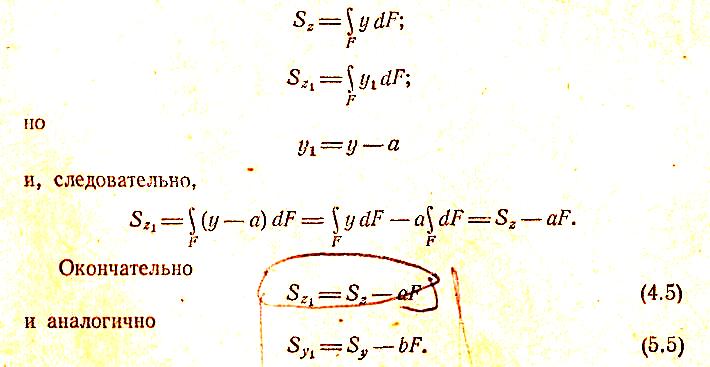
Найдем теперь
положение осей z₁
и y₁
(рис. 4.5),
относительно которых статические
моменты равны нулю. Для этого приравняем
нулю выражения (4.5)
и (5.5):

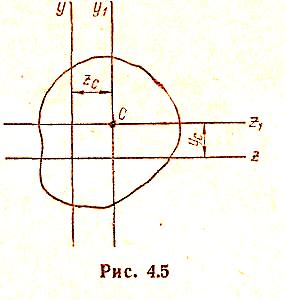
Точка пересечения
таких осей
(точка С на
рис. 4.6) называется
центром тяжести
сечения, а оси
проходящие через центр тяжести, —
центральными
осями. Относительно
любой оси, проходящей через центр тяжести
сечения (т.е. относительно любой
центральной оси), статический момент
равен нулю. Формулы
(6.5) используются для определения
координат центра тяжести сечения.

Для сложного
сечения, установим следующий порядок
определения положения центра тяжести

1. Сложное сечение
   разбивается на части, имеющие вид
   простых фигур.

2. Определяются
   площади и положения центров тяжести
   каж­дой фигуры.

3. Выбираются
   случайные координатные оси у
   и z.

4. По формулам (6.5)
вычисляются статические моменты Sⁱ_v
и Sⁱ_z
относительно
осей у и
z
каждой фигуры.
Затем путем суммирования значений [в
соответствии с выражениями (3.5)]
определяется статические моменты S_y,
S_z
всего сечения.

5. По формулам (6.5)
вычисляются координаты центра тяжести
всего сечения.

В отдельных случаях,
когда заданное сечение нельзя разбить
на такие фигуры, положения центров
тяжести которых известны, положение
центра тяжести всего сечения необходимо
определять путем непосредственного
интегрирования.

2. Моменты инерции сечений

Осевым (или
экваториальным) моментом инерции сечения
относительно некоторой оси называется
взятая по всей его площади F
сумма произведений элементарных
плош.адок dF
на квадраты, их расстояний от этой оси,
т. е.

Полярным моментом
инерции сечения относительно некоторой
точки (полюса) называется взятая по всей
его площади F
сумма произведений элементарных площадок
dF
на квадраты их расстояний от этой точки,
т. е.

Центробежным
моментом инерции сечения относительно
некоторых двух взаимно перпендикулярных
осей называется взятая по
всей его
площади F
сумма произведений элементарных площадок
dF
на их расстояния от этих осей,
т. е.

Моменты инерции
выражаются в см⁴,
м⁴
и т. д.

Осевые и полярные
моменты инерции всегда положительны,
так как в их выражения под знаки интегралов
входят величины площадок dF
(всегда
положительные) и квадраты
расстояний этих площадок от данной оси
или полюса.

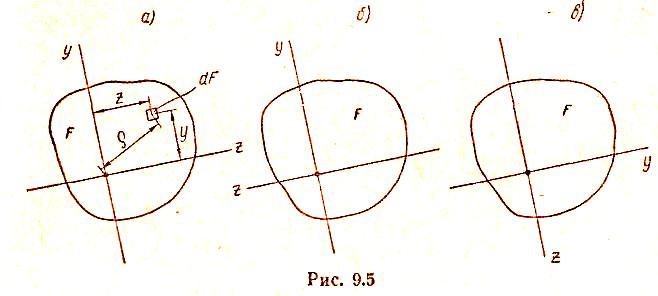
На рис. 9.5,а изображено
сечение площадью F
и показаны оси
у и
z.
Осевые моменты
инерции этого сечения относительно
осей у и z
:

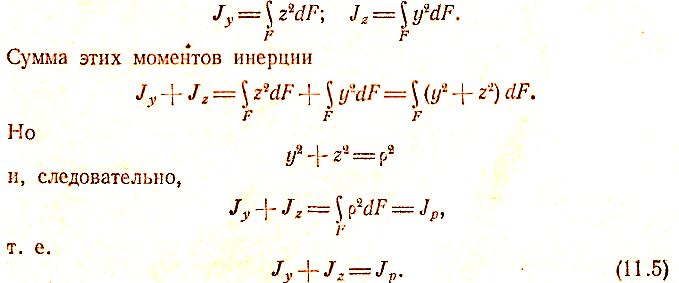
Таким образом,
сумма осевых
моментов инерции сечения- относительно
двух взаимно перпендикулярных осей
равна полярному моменту инерции этого
сечения относительно точки пересечения
указанных осей.

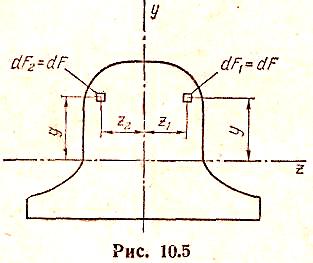
Рассмотрим фигуру,
симметричную относительно одной или
нескольких осей (рис. 10.5). Проведем оси
у и
z
так, чтобы хотя
бы одна из них (в данном случае ось у)
совпадала с
осью симметрии фигуры. Каждой площадке
dF₁,
расположенной
справа от оси и,
соответствует
в этом случае такая же площадка dF₁
расположенная
симметрично первой, но слева от оси у.
Центробежный
момент инерции каждой пары таких
симметрично расположенных площадок
равен:

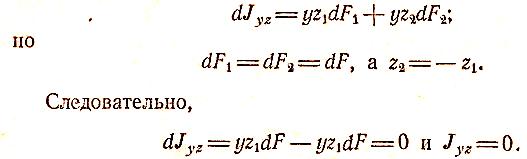
Таким образом,
центробежный
момент инерции сечения относительно
осей, из которых одна или обе совпадают
с его осями симметрии, равен нулю.

Осевой момент
инерции сложного сечения относительно
некоторой оси равен сумме осевых моментов
инерции составляющих его частей
относительно этой же оси.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Меню сайта

Базовый курс лекций по сопромату, теория, практика, задачи.

::Оглавление::

:: Посмотреть новый вариант этой лекции::

:: Пример расчета ::

:: Расчет характеристик он-лайн (программа) ::

1. Геометрические характеристики сечений.

1.1. Статический момент сечения.

При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.

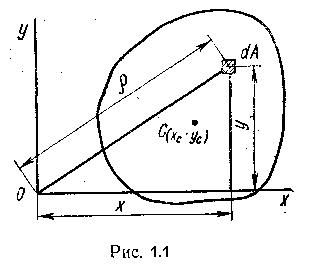
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида

          (1.1)

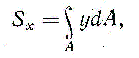
где y — расстояние от элементарной площадки dA до оси x.

Единицей измерения статического момента является единица длины в третьей степени, обычно см³(см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать

          (1.2)

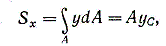
где А — площадь всей фигуры (равнодействующая); ус — расстояние от центра тяжести фигуры до оси х.

Из формулы (1.2) следует формула определения ординаты центра тяжести

ус = Sx/A.           (1.3)

Аналогично, статический момент относительно оси у равен

          (1.4)

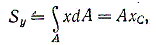
Откуда

xс = Sy/A.           (1.5)

Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.

Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.

Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.

Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.

Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:

          (1.1a)

          (1.4a)

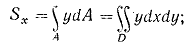
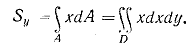
Здесь D — облать интегрирования.

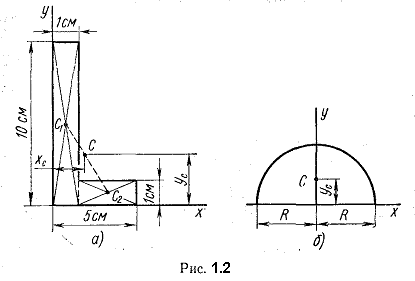
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.

Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.

По формулам (1.3) и (1.5) получим:

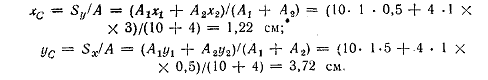
По этим координатам находим точку С — центр тяести сечения. Она лежит на линии, соединяющей точки С1 и С2, ближе к фигуре, имеющей большую площадь.

Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).

Решение. Пользуемся формулой

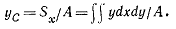
Вычисляем числитель, используя уравнение окружности х² + y² = R²:

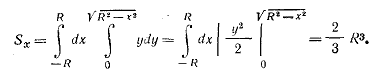
Вычисляем ус

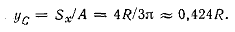
Полезные ссылки

1. Пример расчета геометрических характеристик

2. Расчет характеристик он-лайн (программа)

::Оглавление::

Сообщество

Вход

Решение задач

Расчет редукторов

Для Android (рекомендую)

Java 2 ME