Как найти статическое отклонение - Исправление недочетов и поиск решений вместе с Examum.ru

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

среднеквадратическое отклонение,
среднее квадратическое отклонение,
среднеквадратичное отклонение,
квадратичное отклонение,
стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

в финансах в качестве меры волатильности,
в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

А -> (19 + 21 + 19+ 21) / 4 = 20
Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

стандартное отклонение компании A = 1,
стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

стандартное отклонение формула, среднее квадратичное отклонение формула, среднеквадратическое отклонение формула, среднее квадратическое отклонение формула

Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с «n–1»),
полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

Вычесть среднее значение из каждого числа
Возвести каждый результат в квадрат (так получатся квадраты разностей)
Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Дисперсия и стандартное отклонение расчёт дисперсии формула

Где:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

при <10% выборка слабо вариабельна,
при 10% – 20 % — средне вариабельна,
при >20 % — выборка сильно вариабельна.

Узнайте также про:

Корреляции,
Метод Крамера,
Метод наименьших квадратов,
Теорию вероятностей
Интегралы.

Источник

1
Look at your data set. This is a crucial step in any type of statistical calculation, even if it is a simple figure like the mean or median.^[2]
- Know how many numbers are in your sample.
- Do the numbers vary across a large range? Or are the differences between the numbers small, such as just a few decimal places?
- Know what type of data you are looking at. What do your numbers in your sample represent? this could be something like test scores, heart rate readings, height, weight etc.
- For example, a set of test scores is 10, 8, 10, 8, 8, and 4.
2
Gather all of your data. You will need every number in your sample to calculate the mean.^[3]
- The mean is the average of all your data points.
- This is calculated by adding all of the numbers in your sample, then dividing this figure by the how many numbers there are in your sample (n).
- In the sample of test scores (10, 8, 10, 8, 8, 4) there are 6 numbers in the sample. Therefore n = 6.
Advertisement
3
Add the numbers in your sample together. This is the first part of calculating a mathematical average or mean.^[4]
- For example, use the data set of quiz scores: 10, 8, 10, 8, 8, and 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. This is the sum of all the numbers in the data set or sample.
- Add the numbers a second time to check your answer.
4
Divide the sum by how many numbers there are in your sample (n). This will provide the average or mean of the data.^[5]
- In the sample of test scores (10, 8, 10, 8, 8, and 4) there are six numbers, so n = 6.
- The sum of the test scores in the example was 48. So you would divide 48 by n to figure out the mean.
- 48 / 6 = 8
- The mean test score in the sample is 8.

1
Find the variance. The variance is a figure that represents how far the data in your sample is clustered around the mean.^[6]
- This figure will give you an idea of how far your data is spread out.
- Samples with low variance have data that is clustered closely about the mean.
- Samples with high variance have data that is clustered far from the mean.
- Variance is often used to compare the distribution of two data sets.
2
Subtract the mean from each of your numbers in your sample. This will give you a figure of how much each data point differs from the mean.^[7]
- For example, in our sample of test scores (10, 8, 10, 8, 8, and 4) the mean or mathematical average was 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 8 = 2, 8 — 8 = 0, 8 — 8 = 0, and 4 — 8 = -4.
- Do this procedure again to check each answer. It is very important you have each of these figures correct as you will need them for the next step.
3
Square all of the numbers from each of the subtractions you just did. You will need each of these figures to find out the variance in your sample.^[8]
- Remember, in our sample we subtracted the mean (8) from each of the numbers in the sample (10, 8, 10, 8, 8, and 4) and came up with the following: 2, 0, 2, 0, 0 and -4.
- To do the next calculation in figuring out variance you would perform the following: 2², 0², 2², 0², 0², and (-4)² = 4, 0, 4, 0, 0, and 16.
- Check your answers before proceeding to the next step.
4
Add the squared numbers together. This figure is called the sum of squares.^[9]
- In our example of test scores, the squares were as follows: 4, 0, 4, 0, 0, and 16.
- Remember, in the example of test scores we started by subtracting the mean from each of the scores and squaring these figures: (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- The sum of squares is 24.
5
Divide the sum of squares by (n-1). Remember, n is how many numbers are in your sample. Doing this step will provide the variance. The reason to use n-1 is to have sample variance and population variance unbiased. ^[10]
- In our sample of test scores (10, 8, 10, 8, 8, and 4) there are 6 numbers. Therefore, n = 6.
- n-1 = 5.
- Remember the sum of squares for this sample was 24.
- 24 / 5 = 4.8
- The variance in this sample is thus 4.8.

1
Find your variance figure. You will need this to find the standard deviation for your sample.^[11]
- Remember, variance is how spread out your data is from the mean or mathematical average.
- Standard deviation is a similar figure, which represents how spread out your data is in your sample.
- In our example sample of test scores, the variance was 4.8.
2
Take the square root of the variance. This figure is the standard deviation.^[12]
- Usually, at least 68% of all the samples will fall inside one standard deviation from the mean.
- Remember in our sample of test scores, the variance was 4.8.
- √4.8 = 2.19. The standard deviation in our sample of test scores is therefore 2.19.
- 5 out of 6 (83%) of our sample of test scores (10, 8, 10, 8, 8, and 4) is within one standard deviation (2.19) from the mean (8).
3
Go through finding the mean, variance and standard deviation again. This will allow you to check your answer.^[13]
- It is important that you write down all steps to your problem when you are doing calculations by hand or with a calculator.
- If you come up with a different figure the second time around, check your work.
- If you cannot find where you made a mistake, start over a third time to compare your work.

Practice Problems and Answers

Add New Question

Question

What is the standard deviation of 10 samples with a mean of 29.05?

Depends on the 10 samples of data. If all ten numbers were 29.05 then the standard deviation would be zero. Standard deviation is a measure of how much the data deviates from the mean.
Question

How do I calculate the standard deviation of 5 samples with the mean of 26?

You take the average of 26 and 5, divide by b squared and multiply by deviation equation constant.
Question

How do I find the standard deviation of 10 samples with a mean of 29.05?

Take each sample and subract the mean. Next, square each result, getting rid of the negative. Add the 10 results and divide the sun by 10 — 1 or 9. That is the standard deviation.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate standard deviation, start by calculating the mean, or average, of your data set. Then, subtract the mean from all of the numbers in your data set, and square each of the differences. Next, add all the squared numbers together, and divide the sum by n minus 1, where n equals how many numbers are in your data set. Finally, take the square root of that number to find the standard deviation. To learn how to find standard deviation with the help of example problems, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 2,560,276 times.

Reader Success Stories

«This article was the best statistics instructor I have ever been taught by. I have learned more from this little…» more

Did this article help you?

Источник

Статистические величины, такие как стандартное отклонение и математическое ожидание, полезны при оценке эффективности или характеристик устройства, системы или процесса, смоделированных с помощью COMSOL Multiphysics^®. В этой статье мы рассмотрим функции, графики и другие инструменты COMSOL Multiphysics, предназначенные для расчёта и визуализации статистических величин.

Статистика: вводный обзор

Статистические методы позволяют рассчитать количественные характеристики случайной величины или большого массива данных. Ниже в таблице перечислены некоторые статистические величины, а также названия операторов и операций над массивами данных, которые используются для их вычисления в COMSOL Multiphysics:

Величина	Параметр	Оператор	Операция над массивом данных
Среднее значение или математическое ожидание	mu	`mean, timeavg`	Average
Стандартное отклонение	sigma	`stddev`	Standard deviation
Дисперсия	Var, sigma^2	–	Variance

Теперь расшифруем смысл каждой из перечисленных выше статистических величин:

Среднее или математическое ожидание (в уравнении ниже обозначается как mu) равно сумме всех значений, отнесённой к числу элементов в массиве данных. Этот статистический показатель даёт полезную информацию об уровне любой колеблющейся величины. Среднее значение чувствительно к так называемым выбросам (то есть элементам выборки, значения которых сильно отличаются от значений других элементов). Ещё одним, схожим по смыслу статистическим параметром является медиана — срединное значение, которое находится в середине упорядоченного по возрастанию массива данных (либо полусумма соседних значений, если число элементов в массиве чётное). Например, оператор timeavg в COMSOL Multiphysics позволяет рассчитать среднее значение зависящей от времени величины в заданном интервале времени.
Стандартное отклонение (обозначается ниже как sigma) характеризует степень отклонения данных от среднего значения. Определяется как квадратный корень из дисперсии. В отличие от дисперсии, стандартное отклонение исчисляется в тех же единицах измерения, что и исходные данные.
Дисперсия (обозначается как Var) является мерой разброса значений относительно ее математического ожидания. Единица измерения дисперсии — это квадрат единицы измерения исходных данных.

Математическое ожидание mu можно рассчитать по формуле:

mu(X)=frac{1}{n}sum_{i=1}^nx_i cdot

Следующее соотношение позволяет определить дисперсию:

Var(X)=frac{1}{n}sum_{i=1}^{n}(x_i-mu)^2

Здесь X — это величина, дисперсию (и среднее значение) которой нужно рассчитать, x_i — массив значений этой величины, mu — математическое ожидание. Это определение дисперсии справедливо для массива данных с фиксированным числом элементов.

В COMSOL Multiphysics X и x_i представляют собой фиксированный массив данных.

Стандартное отклонение sigma равно квадратному корню из дисперсии:

sigma = sqrt{text{Var}}

Эти формулы можно легко обобщить на случай расчёта статистических величин, определённых на геометрических объектах, если заменить суммирование на интегрирование по пространству. Именно такое обобщение и используется в COMSOL Multiphysics. Интегральная форма соотношения для расчёта средней величины X по области Omega имеет вид:

mu(X) = frac{1}{|Omega|}int_Omega x dOmega

и, аналогично, дисперсия переменной X по области Omega равна

Var(X) = frac{1}{|Omega|}int_Omega (x-mu(x))^2 dOmega

где |Omega| — размер области (объём, площадь или длина, в зависимости от пространственной размерности модели).

В следующих параграфах мы объясним, как использовать все эти операции и операторы при моделировании в COMSOL Multiphysics.

Статистические величины в COMSOL Multiphysics

Нелокальные операторы

Позже мы рассмотрим, как использовать встроенный оператор stddev для вычисления стандартного отклонения. Но перед этим давайте обсудим, как рассчитать среднее значение величины, например, в объёме или вдоль границ: кликните правой кнопкой мыши по узлу Definitions в текущем компоненте Component, а затем выберите пункт Average в меню Nonlocal Couplings. Так мы добавляем оператор осреднения с именем по умолчанию aveop1, а затем в настройках этого оператора указываем тип геометрического объекта Geometric entity level (например, Boundary) и выбираем сам объект (например, границы области), в пределах которого нужно выполнить осреднение. Аналогичным образом в дерево модели можно добавить операторы для расчёта интегралов, максимальных и минимальных значений.

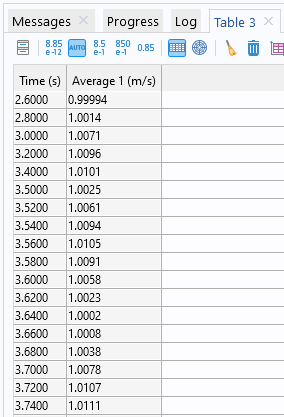
Добавленные операторы можно использовать как в процессе расчёта модели, так и на этапе обработки результатов. Например, в задачах вычислительной гидродинамики с помощью оператора осреднения можно рассчитать среднюю скорость среды в выходном сечении расчётной области. Для этого в ветке Results дерева модели к узлу Derived Values нужно добавить подузел Global Evaluation, в окне настройки которого нужно ввести выражение aveop1(spf.U) и нажать кнопку Evaluate. После этого рассчитанные значения средней скорости для каждого сохранённого момента времени нестационарной задачи появятся в окне Table.

Окно Table, в которое выводятся значения средней скорости для каждого сохранённого момента времени.

Стандартное отклонение или дисперсию можно рассчитать с помощью повторного использования нелокального оператора: сначала с помощью оператора вычисляется среднее значение, а затем тот же оператор используется для расчёта стандартного отклонения или дисперсии. Например, в нашем примере с гидродинамической задачей для определения стандартного отклонения давления на выходной границе можно воспользоваться оператором осреднения aveop1, заданным на выходной границе. Для этого в окне настройки узла Global Evaluation введём выражение sqrt(aveop1((aveop1(p)-p)^2)).

Упрощение выражений с помощью оператора Expression Operator

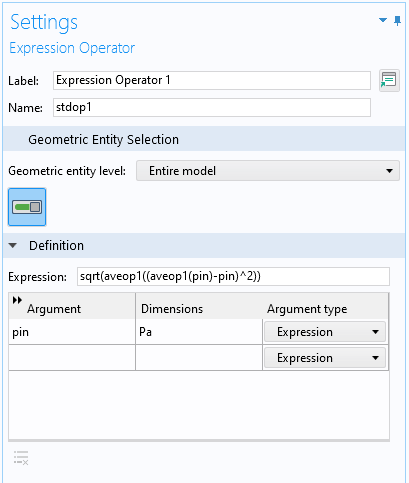
Выражение sqrt(aveop1((aveop1(p)-p)^2)), которое мы использовали выше, длинновато. Чтобы упростить использование этого выражения для настройки расчётной модели, можно воспользоваться оператором Expression Operator. Для этого сначала включим опцию Variable Utilities в разделе General окна настройки дерева модели Show More Options. Затем добавим узел Expression Operator из контекстного меню Variable Utilities, которое можно вызвать, кликнув правой кнопкой мыши по узлу Definitions текущего компонента модели Component. В окне настройки узла Expression Operator даём новому оператору название, например, stdop1 и вводим его определение, используя то же самое выражение, но уже с произвольным аргументом, который мы обозначим, скажем, pin:

Окно настройки Settings узла Expression Operator, который позволяет дать определение упрощённому оператору stdop1 для расчёта стандартного отклонения.

Теперь этот оператор можно использовать для обработки результатов моделирования, вводя команду stdop1(p) вместо sqrt(aveop1((aveop1(p)-p)^2)).

Производные величины

На этапе обработки результатов можно добавить узлы для расчёта среднего по объёму Volume Average, по поверхности Surface Average и вдоль контура Line Average, если воспользоваться контекстным меню узла Derived Values и выбрать соответствующую команду из подменю Average. Аналогично можно добавить узлы для вычисления интегральных Integration, максимальных Maximum и минимальных Minimum значений.

Преобразование результатов нестационарных и параметрических исследований

Для обработки массива данных, полученных в результате нестационарного, параметрического исследования или исследования на собственные значения, с помощью узла Point Evaluation можно вычислить следующие значения:

Среднее
Интегральное
Максимальное или минимальное
Среднеквадратическое (RMS)
Стандартное отклонение
Дисперсию

Результатом каждой из этих операций является одно число, которое представляет собой, например, среднее значение всех результатов параметрического исследования или стандартное отклонение переменной нестационарной модели в точке.

Встроенные операторы

В COMSOL Multiphysics доступно большое количество физических переменных, а также встроенных физических и математических констант, функций и операторов, которые можно использовать для обработки и визуализации результатов моделирования. Вы можете ввести имя непосредственно в любое поле Expression или выбрать из списка, нажав кнопку Add Expression или Replace Expression (кнопки расположены на панели инструментов раздела Expression). На скриншоте ниже показаны операторы из группы Integration and statistics COMSOL Multiphysics^® версии 6.0:

Встроенные операторы группы Integration and statistics.

Особый интерес представляет оператор stddev для вычисления стандартного отклонения. С его помощью можно рассчитать стандартное отклонение давления на выходной границе в описанном выше примере, если ввести выражение stddev('comp1.aveop1',p). Это более простой и эффективный синтаксис, чем последовательное обращение к оператору осреднения, которые мы использовали выше для определения стандартного отклонения. Отметим, что имена компонентов и операторов в выражении приведены для примера, и в ваших моделях они могут быть иными.

Стандартное отклонение и математическое ожидание: пример

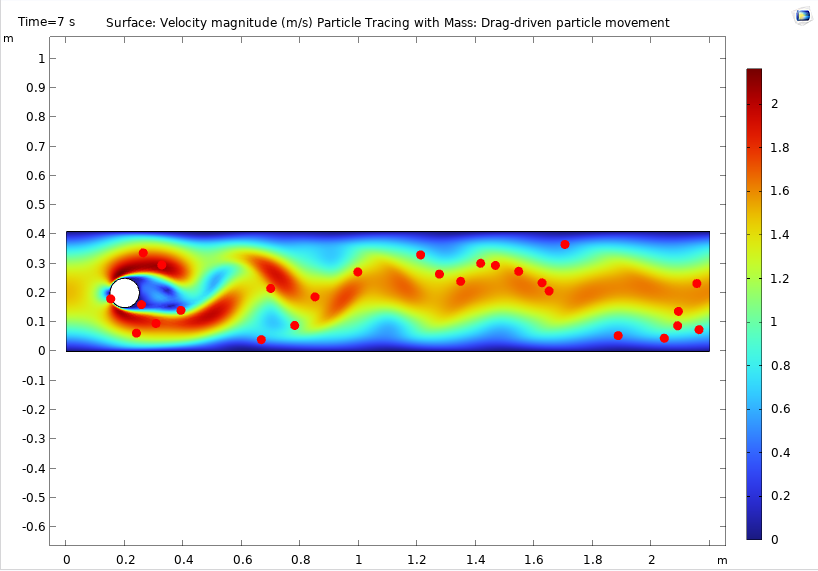
Давайте рассчитаем парочку статистических характеристик в нестационарной модели обтекания цилиндра Flow Past a Cylinder model, которую можно найти в разделе Fluid Dynamics библиотеки приложений Application Library в COMSOL Multiphysics. Вычислим следующие величины:

Среднее значение и стандартное отклонение давления в расчётной области во всём временном интервале моделирования
Среднее значение и стандартное отклонение скорости в некоторой точке выходной границы во всём временном интервале моделирования

Построенный по умолчанию график в модели обтекания цилиндра Flow Past a Cylinder, показывающий распределение скорости и частиц в момент времени 7 с.

Среднее значение и стандартное отклонение давления в домене и на выходной границе

Чтобы определить среднее значение и стандартное отклонение давления в какой-то области, сначала добавим узел Average с названием оператора, скажем, aveop2, и выберем область осреднения. (В рассматриваемой геометрической модели существует только один домен). После завершения расчёта добавим подузел Global Evaluation к узлу Derived Values ветки Results дерева модели, и в окне настройки этого подузла введём выражение aveop2(p). Искомое значение среднего по объёму давления появится в окне Table для всех моментов времени, указанных в списке Time selection (по умолчанию выбраны все сохранённые моменты времени). Если нужно рассчитать среднее по времени значение осреднённого по объёму давления, выберите опцию Average из списка Transformation в разделе Data Series Operation. В результате получится одно скалярное число для среднего по времени значения осреднённого давления. Чтобы вывести стандартное отклонение на каждом шаге по времени, введите также выражение stddev('comp1.aveop2',p) (или воспользуйтесь любым из упомянутых выше вариантов расчёта).

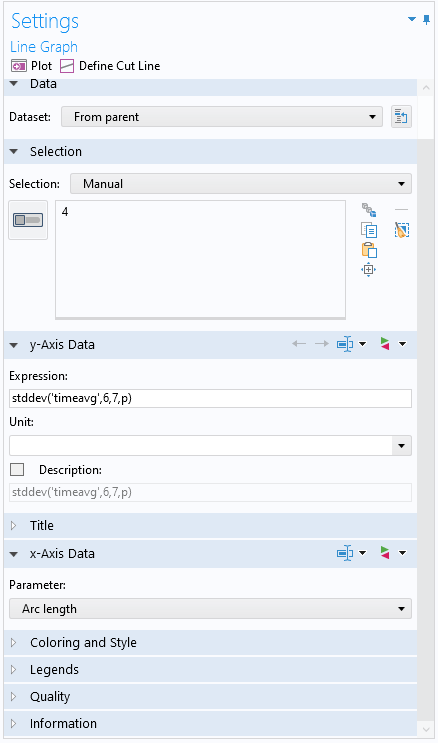
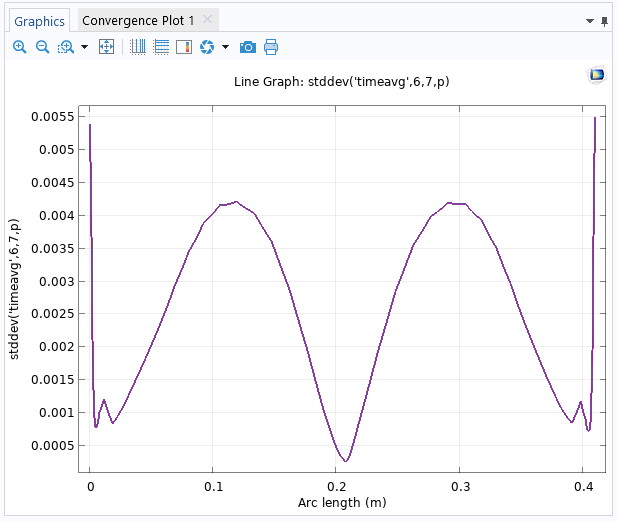
Аргумент оператора stddev не обязательно должен быть средним значением. Например, в качестве аргумента можно ввести оператор интегрирования, но результатом по-прежнему будет правильно рассчитанное значение стандартного отклонения. Кроме того, его можно использовать в комбинации с оператором timeavg, чтобы получить тот же результат, что и в результате использования операций над массивами данных. Это можно сделать с помощью выражения типа stddev('timeavg',t1,t2,expr), где t1 и t2 — начальный и конечный моменты временного интервала, а expr — это выражение, которое нужно осреднить в заданном временном интервале. Например, чтобы построить график стандартного отклонения давления во временной области для каждой точки выходной границы в интервале времени от 6 до 7 секунд, можно использовать выражение stddev('timeavg',6,7,p).

Окно настройки Settings графика Line Graph, в котором используется выражение для расчёта стандартного отклонения во временной области в интервале времени от 6 до 7 секунд.

График показывает, что наименьшее значение стандартного отклонения давления достигается в срединной точке выходной границы.

Одномерный график Line Graph стандартного отклонения давления во временной области на выходной границе.

Среднее значение и стандартное отклонение скорости на выходной границе

Если нужно определить среднее значение и стандартное отклонение скорости в срединной точке выходной границы на каждом шаге по времени, то сначала надо найти значение скорости в этой точке. Это можно сделать двумя способами:

Добавить в геометрическую модель точку посередине выходной границы, даже если эта точка не используется в самой модели
Добавить набор данных Cut Point (в нашем случае Cut Point 2D), а затем задать координаты точки в окне настройки набора данных

Чтобы найти скорость в средней точке, используйте узел Point Evaluation, в окне настройки которого либо выберите нужную точку в геометрической модели, либо выберите в качестве входных данных для графика набор данных Cut Point 2D. Затем в качестве входной переменной для графика укажите, например, spf.U. В разделе Data Series Operation окна настройки выберите Average или Standard deviation. Кликнув по кнопке Evaluate, расположенной в верхней части окна настройки Settings, вы получите график среднего значения или стандартного отклонения (оба в м/с) для скорости в средней точке выходной границы на каждом сохранённом временном шаге исследования.

Среднее значение и стандартное отклонение скорости выводятся в таблицу в окне Table.

Гистограммы

С помощью гистограмм удобно визуализировать форму и разброс некоторых массивов данных. В COMSOL Multiphysics встроены следующие типы гистограмм:

Гистограммы Histogram (1D и 2D графики) показывают, как та или иная величина распределена в пространстве в пределах геометрических объектов. В одномерных гистограммах по оси x отложены значения величины (в виде интервалов), а по оси y — общее число элементов в каждом интервале.
Табличные гистограммы Table Histogram (1D и 2D графики) аналогичны обычным гистограммам Histogram, но строятся на основе данных из таблицы или расчётной группы.
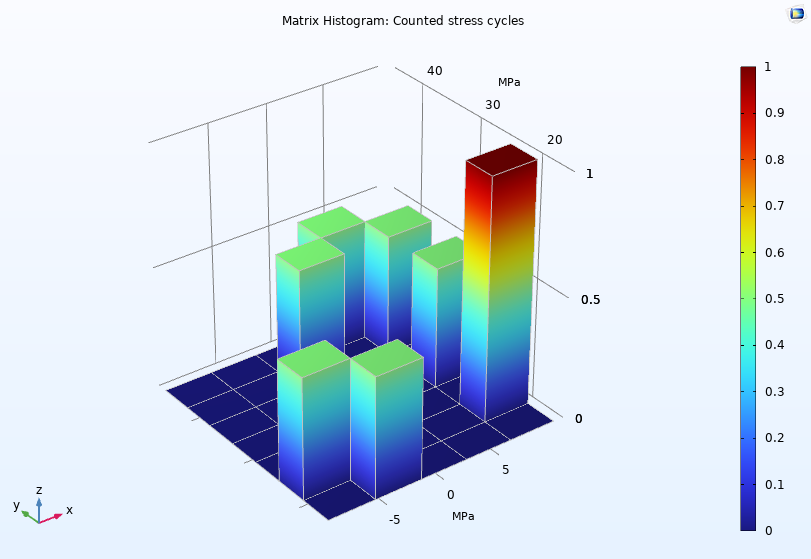
Матричные гистограммы Matrix Histogram (только 2D графики) позволяют визуализировать матрицы в виде 2D гистограмм.

При построении графиков Histogram и Table Histogram можно выбрать, хотите вы задать количество столбиков на гистограмме или диапазон значений для каждого столбика гистограммы. Для 2D гистограмм можно добавить подузел Height Expression, чтобы придать столбикам трёхмерный вид за счет использования оси z, как показано на рисунке ниже.

График Matrix Histogram показывает число циклов нагружения, рассчитанное в верификационной модели Cycle Counting in Fatigue Analysis — Benchmark model.

Оценка неопределённости и статистика

С помощью модуля «Оценка неопределённости», дополняющего функционал среды COMSOL Multiphysics, можно получить статистические данные, связанные с количественной оценкой неопределённости, непосредственно в таблицах выходных данных. Например, для анализа распространения неопределенности с использованием неадаптивных суррогатных режимов гауссовского процесса доступны следующие четыре таблицы:

Таблица доверительных интервалов QoI Confidence interval, в которой для каждой целевой переменной выводятся данные о математическом ожидании, стандартном отклонении, минимальном и максимальном значениях, а также о доверительных интервалах для доверительных вероятностей 90%, 95% и 99%.
Таблица UP predicted QoI, в которой приведены спрогнозированные суррогатной моделью значения целевых переменных для точек выборки метода Монте-Карло.
Таблица спрогнозированных значений стандартного отклонения UP predicted standard deviation, в которой указаны спрогнозированные суррогатной моделью стандартные отклонения для точек выборки метода Монте-Карло. Эти данные можно интерпретировать как встроенную оценку погрешности суррогатной модели.
Таблица максимальных значений энтропии Maximum entropy, в которой указаны максимальные относительные значения стандартного отклонения для каждой целевой переменной.

При использовании адаптивной суррогатной модели гауссовского процесса в группу выходных таблиц также добавляются четыре соответствующие адаптивные таблицы результатов. Они содержат информацию о результатах на всех этапах адаптации.

Дальнейшие шаги

В качестве следующего шага попробуйте использовать некоторые из этих статистических инструментов в своих собственных расчётных моделях; так вы сможете получить статистические характеристики и количественные оценки целевых переменных или параметров. Если у вас возникли вопросы по данной теме, свяжитесь с COMSOL с помощью этой кнопки.

Источник

Определение стандартного отклонения

Стандартное отклонение измеряет величину вариации или дисперсии в наборе значений данных относительно его среднего значения (среднего). Это статистический инструмент, используемый для интерпретации надежности данных. Он представлен символом «σ».

Если отклонение меньше, точки данных близки к среднему значению, и данные считаются
надежный. Напротив, если отклонение велико, точки данных разбросаны дальше от среднего значения; такие данные считаются менее надежными. Стандартное отклонение используется при анализе общего риска и доходности портфеля.

Оглавление

Определение стандартного отклонения
- Объяснение стандартного отклонения
- Уравнение стандартного отклонения
- Расчет
- Пример
- Интерпретация
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Стандартное отклонение — это статистический инструмент, который измеряет волатильность данных. Он указывает, в какой степени значения выборки отклоняются от средних значений. Он вычисляется как квадратный корень из дисперсии и обозначается символом «σ» (греческая буква).
σ не может быть отрицательным значением и может быть равен 0 только в том случае, если значения в наборе данных равны и не имеют вариаций.
В финансах этот математический инструмент применяется для определения уровня рисков, связанных с конкретными инвестициями или активами. Метод измеряет спред соответствующих цен и доходов. Более высокое отклонение отражает высокую волатильность и наоборот.
Если символ σ обозначает стандартное отклонение, n — общее количество наблюдений в наборе данных, xi — i-е количество наблюдений, а µ — выборочное среднее, то отклонение вычисляется по следующей формуле:

В большинстве случаев минимальное стандартное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Этот статистический инструмент помогает исследователям и аналитикам понять распространение данных, чтобы
определить степень разброса данных. Этот математический аппарат показывает
разброс выборочных значений от среднего значения.

Стандартные ошибки подчеркивают точность среднего значения выборки по отношению к генеральной совокупности.
означает, когда данные обширны и широко распространены. На графике отклонение может лежать влево, вправо или в обе стороны — формирование колоколообразной кривойГрафик колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее.

Уравнение стандартного отклонения

Уравнение для определения стандартного отклонения ряда данных выглядит следующим образом:

т.е. σ=√v

Также, µ =∑x/n

Здесь,

σ — это символ, обозначающий стандартное отклонение.
n — количество наблюдений в наборе данных.
xi — i-е количество наблюдений в наборе данных.
µ — среднее значение выборки.
V — дисперсия.
∑x — сумма всех значений в наборе данных.

Расчет

Основные шаги, используемые для поиска и расчета стандартного отклонения, следующие:

Сначала определите среднее значение набора данных.
Затем подготовьте диаграмму со значениями выборки и разницей между выборкой.
значения и средние значения.
В следующем столбце найдите квадрат разностей.
Чтобы получить дисперсию, сложите все квадраты и разделите результат на разницу между общим количеством наблюдений и 1.
Наконец, найдите квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Пример

Давайте рассмотрим несколько примеров, чтобы понять практические последствия:

Найти отклонение цен на сырую нефть за год, когда среднемесячные цены за литр были следующими:

МесяцСредняя цена за литр в долларахЯнварь0,83Февраль0,81Март0,78Апрель0,82Май0,79Июнь0,75Июль0,76Август0,79Сентябрь0,81Октябрь0,77Ноябрь0,76Декабрь0,75

Решение:

Расчет среднего:

µ = ∑x/n

µ = 9,42/12

= 0,785 доллара за литр

С. №МесяцСредняя цена за литр в $ (x)х – 0,785 доллара США(х – 0,785 долл. США)21January0.830.0450.0020252February0.810.0250.0006253March0.78-0.0050.0000254April0.820.0350.0012255May0.790.0050.0000256June0.75-0.0350.0012257July0.76-0.0250.0006258August0.790.0050.0000259September0.810.0250.00062510October0.77-0.0150.00022511November0. 76-0.0250.00062512декабрь0.75-0.0350.00122512–9.42 0,0085

Расчет стандартного отклонения :

σ = √ [0.0085 / (12-1)]
σ = √ (0,00077272727)
σ = 0,0277979724571285 долл. США

Таким образом, стандартное отклонение цен на нефть за литр для данного года равно
0,0277979724571285.

Интерпретация

Стандартное отклонение указывает на волатильность или дисперсию значений конкретного распределения. Он показывает, в какой степени значения выборки отклоняются от средних значений. Таким образом, эта мера облегчает сравнение и анализ.

Ниже приведены различные интерпретации полученного результата:

Если σ велико, то волатильность анализируемых данных также высока.
Точно так же, когда σ низкое, дисперсия между точками данных также незначительна.
В распределении σ может быть равно 0 только тогда, когда разница между точками данных равна нулю. Это также наименьшее значение отклонения, которое можно получить.
Невозможно получить отрицательное значение σ, так как числитель включает квадрат разности между выборочными значениями и средними значениями.
Кроме того, количество наблюдений всегда больше 1; следовательно, знаменатель должен быть положительным значением.
Стандартное отклонение измеряется в тех же единицах, что и значения распределения. Например, в приведенном выше примере σ выражается в долларах.
Выбросы (чрезвычайно высокие или низкие значения) существенно влияют на измерения отклонения.

Часто задаваемые вопросы (FAQ)

Что такое стандартное отклонение?

Стандартное отклонение — это статистический метод, используемый для нахождения разброса данных в распределении с использованием средних значений. Обозначается символом «σ».

Как рассчитать стандартное отклонение?

Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Дисперсия — это сумма квадрата разности между каждым значением в наборе данных и их средними значениями, деленная на значение, полученное путем вычитания единицы из общего числа наблюдений.

Почему стандартное отклонение важно?

Он определяет степень изменчивости значений в выборочном распределении. Это широко используемый статистический инструмент в финансах, инвестициях и бизнесе для интерпретации величины риска, связанного с ценной бумагой или активом. В большинстве случаев минимальное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Может ли стандартное отклонение быть равным нулю?

Единственный случай, когда он может быть равен нулю, — это когда все точки данных в распределении одинаковы. Нулевое отклонение указывает на нулевой разброс или изменчивость значений. Для реальных сценариев это практически невозможно.

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Использование и интерпретация величины среднеквадратического отклонения

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Пример 2 (с S)

Дисперсия и стандартное отклонение

Правило трёх сигм

Стандартное отклонение в excel

Коэффициент вариации

Practice Problems and Answers

Video

References

About This Article

Reader Success Stories

Did this article help you?

Статистика: вводный обзор

Статистические величины в COMSOL Multiphysics

Нелокальные операторы

Упрощение выражений с помощью оператора Expression Operator

Производные величины

Преобразование результатов нестационарных и параметрических исследований

Встроенные операторы

Стандартное отклонение и математическое ожидание: пример

Среднее значение и стандартное отклонение давления в домене и на выходной границе

Среднее значение и стандартное отклонение скорости на выходной границе

Гистограммы

Оценка неопределённости и статистика

Дальнейшие шаги

Определение стандартного отклонения

Уравнение стандартного отклонения

Расчет

Пример

Интерпретация

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Что такое дисперсия

Что такое стандартное отклонение

Примечание. Почему именно квадраты разностей?