Статистическая сумма (или статсумма) (обозначается Z, от нем. Zustandssumme — сумма по состояниям) — важная величина в статистической физике, содержащая информацию о статистических свойствах системы в состоянии термодинамического равновесия. Она является функцией температуры и других параметров, таких как объём. Многие термодинамические величины системы, такие как энергия, свободная энергия, энтропия и давление, могут быть выражены через статистическую сумму и её производные.
Существует несколько типов статистической суммы, каждый из которых соответствует различным статистическим ансамблям. Каноническая статистическая сумма относится к каноническому статистическому ансамблю, в котором система может обмениваться с окружающей средой теплотой при фиксированных температуре, объёме и числе частиц. Большая каноническая статистическая сумма относится к большому каноническому статистическому ансамблю, в котором система может обмениваться с окружающей средой как теплотой, так и частицами при фиксированных температуре, объёме и химическом потенциале. В других ситуациях можно определить другие типы статистических сумм.
Статистическая сумма в каноническом ансамбле
Определение
Предположим, что имеется подчиняющаяся законам термодинамики система, находящаяся в постоянном тепловом контакте со средой, которая имеет температуру T, а объём системы и количество составляющих её частиц фиксированы. В такой ситуации система относится к каноническому ансамблю. Обозначим точные состояния, в которых может находиться система, j (j = 1, 2, 3, …), а полную энергию системы в состоянии j — Ej. Как правило, эти микросостояния можно рассматривать как дискретные квантовые состояния системы.
Каноническая статистическая сумма — это
где обратная температура β определена как
а kB — это постоянная Больцмана.
В классической статистической механике было бы некорректно определять статистическую сумму в виде суммы дискретных членов, как в приведенной выше формуле. В классической механике координаты и импульсы частиц могут меняться непрерывно, и множество микросостояний несчётно. В таком случае необходимо провести разбиение фазового пространства на ячейки, то есть два микросостояния считаются одинаковыми, если их различия в координатах и импульсах «не слишком велики». При этом статистическая сумма принимает вид интеграла. Например, статистическая сумма газа из N классических частиц равна
где h — некоторая величина размерности действия (которая должна быть равна постоянной Планка для соответствия квантовой механике), а H — классический гамильтониан. Причины появления множителя N! объяснены ниже. Для простоты в этой статье будет использоваться дискретный вид статистической суммы, но полученные результаты в равной мере относятся и к непрерывному виду.
В квантовой механике статистическая сумма может быть записана более формально как след по пространству состояний (который не зависит от выбора базиса):
где H — оператор Гамильтона. Экспонента от оператора определяется с помощью разложения в степенной ряд.
Смысл и значимость
Из определения сложно понять, почему статистическая сумма является важной величиной. Сначала рассмотрим, от чего она зависит. Статистическая сумма является функцией, в первую очередь, температуры T, а во вторую — энергий микросостояний E1, E2, E3 и т. д. Энергии микросостояний определяются другими термодинамическими величинами, такими как число частиц и объём, а также микроскопическими свойствами, такими как масса частиц. Эта зависимость от микроскопических свойств является основной в статистической механике. По модели микроскопических составляющих системы можно рассчитать энергии микросостояний, а следовательно, и статистическую сумму, которая позволяет рассчитать все остальные термодинамические свойства системы.
Статистическая сумма может быть использована для расчета термодинамических величин, поскольку она имеет очень важный статистический смысл. Вероятность Pj, с которой система находится в микросостоянии j, равна
Статистическая сумма входит в распределение Гиббса в виде нормировочного множителя (она не зависит от j), обеспечивая равенство единице суммы вероятностей:
Вычисление термодинамической полной энергии
Чтобы продемонстрировать полезность статистической суммы, рассчитаем термодинамическое значение полной энергии. Это просто математическое ожидание, или среднее по ансамблю значение энергии, равное сумме энергий микросостояний, взятых с весами, равными их вероятностям:
или, что то же самое
Можно также заметить, что если энергии микросостояний зависят от параметра λ как
для всех j, то среднее значение A равно
На этом основан прием, позволяющий вычислить средние значения многих микроскопических величин. Нужно искусственно добавить эту величину к энергии микросостояний (или, на языке квантовой механики, к гамильтониану), вычислить новую статистическую сумму и среднее значение, а затем в итоговом выражении положить λ равным нулю. Аналогичный метод применяется в квантовой теории поля.
Связь с термодинамическими величинами
В этом разделе приведена связь статистической суммы с различными термодинамическими параметрами системы. Эти результаты могут быть получены с помощью метода, описанного в предыдущем разделе, и различных термодинамических соотношений.
Как мы уже видели, энергия равна
Флуктуация энергии равна
Теплоёмкость равна
Энтропия равна
где F — свободная энергия, определяемая как F = E — TS, где E — полная энергия, а S — энтропия, так что
Статистическая сумма подсистем
Предположим, что система состоит из N подсистем, взаимодействие между которыми пренебрежимо мало. Если статистические суммы подсистем равны ζ1, ζ2, …, ζN, то статистическая сумма всей системы равна произведению отдельных статистических сумм:
Если подсистемы обладают одинаковыми физическими свойствами, то их статистические суммы одинаковы: ζ1 = ζ2 = … = ζ, и в этом случае
Из этого правила, однако, есть одно известное исключение. Если подсистемы — это идентичные частицы, то есть, исходя из принципов квантовой механики, их невозможно различить даже в принципе, общая статистическая сумма должна быть разделена на N! (N факториал):
Это делается, чтобы не учитывать одно и то же микросостояние несколько раз.
Статистическая сумма большого канонического ансамбля
Определение
Аналогично канонической статистической сумме для канонического ансамбля, можно определить большую каноническую статистическую сумму для большого канонического ансамбля — системы, которая может обмениваться со средой и теплотой, и частицами, и имеет постоянную температуру T, объём V и химический потенциал μ;.
Большая каноническая статистическая сумма, хотя и более сложна для понимания, упрощает расчет квантовых систем. Большая каноническая статистическая сумма 
где N — общее количество частиц в объёме V, индекс i пробегает все микросостояния системы, ni — число частиц в состоянии i, а εi — энергия в состоянии i. {ni} — всевозможные наборы чисел заполнения каждого микросостояния, такие что Σini=N.
Рассмотрим, например, слагаемое, соответствующее N=3. Один из возможных наборов чисел заполнения будет {ni} = 0, 1, 0, 2, 0…, он дает вклад в слагаемое с N = 3, равный
Для бозонов числа заполнения могут принимать любые целые неотрицательные значения при том, что их сумма равна N. Для фермионов, в соответствии с принципом запрета Паули, числа заполнения могут быть равны только 0 или 1, но их сумма опять же равна N.
Частные случаи
Можно показать, что указанное выражение для большой канонической статистической суммы математически эквивалентно следующему:
(Это произведение иногда берется по всем значениям энергии, а не по отдельным состояниям, и в этом случае каждая отдельная статистическая сумма должна быть возведена в степень gi;, где gi — число состояний с такой энергией. gi также называется степенью вырождения.)
Для системы, состоящей из бозонов:
а для системы, состоящей из фермионов:
В случае максвелловско-больцмановского газа необходимо корректно подсчитывать состояния и делить больцмановский множитель 
Связь с термодинамическими величинами
Так же как и каноническая статистическая сумма, большую каноническую статистическую сумму можно использовать для вычисления термодинамических и статистических величин системы. Как и в каноническом ансамбле, термодинамические величины не фиксированы, а статистически распределены вокруг среднего значения.
- Обозначая α = −βμ, получаем средние значения чисел заполнения:
Для больцмановских частиц это даёт:
Для бозонов:
Для фермионов:
что совпадает с результатами, получаемыми с помощью канонического ансамбля для статистики Максвелла — Больцмана, статистики Бозе — Эйнштейна и статистики Ферми — Дирака соответственно. (Степень вырождения gi отсутствует в этих уравнениях, поскольку индекс i нумерует отдельные состояния, а не уровни энергии.)
- Общее число частиц
- Флуктуация общего числа частиц
- Внутренняя энергия
- Флуктуация внутренней энергии
- Давление
- Механическое уравнение состояния
Литература
- Huang, Kerson, «Statistical Mechanics», John Wiley & Sons, New York, 1967.
- A. Isihara, «Statistical Physics», Academic Press, New York, 1971.
- Kelly, James J, (Lecture notes)
- L. D. Landau and E. M. Lifshitz, «Statistical Physics, 3rd Edition Part 1», Butterworth-Heinemann, Oxford, 1996.
В
этом месте объясняется, как найти
статистическую сумму реального вещества.
Раньше предполагалось, что потенциальной
энергии системы нету.
Для определения
данного интеграла, что такая потенциальная
энергия это сумма попарных взаимодействий
системы, да такое решение не самое
лучшее, но по лучше ничего не придумали.
Далее определим
(mi-количество
I
частичных групп) с помощью которых можно
определить групповые функции (S).
Тогда (WN)
можно определить как
сумму вкладов всех возможных прономерованных
разбиений групп.
Например.
Даже не смотря на
упрощение задачи определить от суда
контурный интеграл получится, но слишком
сложно. Поэтому будем определять большую
статистическую сумму.
При использование
такого метода вириальные коэффициенты
определяются следующим образом
По
достаточно очевидным причинам на
электрические заряды действует силы,
такие как электрические гравитационные.
Так как гравитационные силы намного
меньше, чем электрические, то принципе
их можно не учитывать по сравнению с
электрическими. Далее рассмотрим, как
определить потенциальную энергию
электрических зарядов дальнейшем будет
показана, что она определяется действиями
электрическим моментами.
Далее,
как известно действие электрического
поля на атом приводит к изменению
электрического поля атома, из-за чего
возникает дополнительный индукционный
дипольный момент, который добавляет
свою часть в потенциальной энергии.
Независимо
от наличии у молекулы, каких то моментов,
она все равно как то взаимодействует с
другой молекулой, такое взаимодействие
называют дисперсионной
взаимодействием.
Это взаимодействие обусловлена
электрическими силами, электроны как
легкие частицы отклоняются от своей
нормальной радиуса, из-за чего и возникает
дополнительный момент. Когда частицы
находятся на большом расстоянии такое
взаимодействие обусловлено притяжением
их друг другу. Когда частицы приблизились
достаточно друг другу, начинают провялятся
квантовые эффекты частиц что приводит
к появлению силы отталкивание друг от
друга.
|
Вещество |
H |
He |
Ne |
Ar |
Kr |
Li |
Na |
Rb |
F |
Cl |
Br |
|
|
4.5 |
1.37 |
2.67 |
11.09 |
16.72 |
162 |
162 |
269 |
3.76 |
15 |
26 |
|
|
6.2 |
1.46 |
6.88 |
66.9 |
135 |
— |
1600 |
3800 |
— |
— |
— |
Потенциалы
Ленардо-Джонса и Букиннгема – это такие
потенциалы, которые описывает слабое
взаимодействие частиц или слабое
Ван-дер-Ваальса взаимодействие.
Следующие
потенциалы для молекулярного взаимодействие
(образование молекулы и фазовые переходы)
Если
взять потенциал Ленардо – Джонса и
безразмерить его, то данная потенциал
будет универсальным для любого вещества.
Если с помощи его определять вириальные
коэффициенты, то они выглядят следующим
образом.
Казалось
бы все хорошо универсальный потенциал
для любого вещества, можно определить
поправку на не идеальность, но это не
так. При малых температурах вириальные
коэффициенты определяются не правильно,
так как начинаю проявляться квантовые
эффекты частиц, из-за чего универсальность
теряется. Приходится водить некоторую
поправку на квантовость в которая входит
число Де Бура, в которой входят уникальные
параметры вещества.
Если усложнить
модель и взять другой потенциал проблема
возникнет примерно такая же, возникнет
элемент в безразмерном виде включающие
уникальные параметры вещества.
Соседние файлы в папке 8 семестр ИТАЭ
- #
- #
Статистическая сумма (или статсумма) (обозначается 
Существует несколько типов статистической суммы, каждый из которых соответствует различным статистическим ансамблям. Каноническая статистическая сумма относится к каноническому статистическому ансамблю, в котором система может обмениваться с окружающей средой теплотой при фиксированных температуре, объёме и числе частиц. Большая каноническая статистическая сумма относится к большому каноническому статистическому ансамблю, в котором система может обмениваться с окружающей средой как теплотой, так и частицами при фиксированных температуре, объёме и химическом потенциале. В других ситуациях можно определить другие типы статистических сумм.
Содержание
- 1 Статистическая сумма в каноническом ансамбле
- 1.1 Определение
- 1.2 Смысл и значимость
- 1.3 Вычисление термодинамической полной энергии
- 1.4 Связь с термодинамическими величинами
- 1.5 Статистическая сумма подсистем
- 2 Статистическая сумма большого канонического ансамбля
- 2.1 Определение
- 2.2 Частные случаи
- 2.3 Связь с термодинамическими величинами
- 3 Литература
Статистическая сумма в каноническом ансамбле[править | править вики-текст]
Определение[править | править вики-текст]
Предположим, что имеется подчиняющаяся законам термодинамики система, находящаяся в постоянном тепловом контакте со средой, которая имеет температуру 




Каноническая статистическая сумма — это
где обратная температура 
а 

где 


В квантовой механике статистическая сумма может быть записана более формально как след по пространству состояний (который не зависит от выбора базиса):
где 
Смысл и значимость[править | править вики-текст]
Сначала рассмотрим, от чего она зависит. Статистическая сумма является функцией, в первую очередь, температуры 

Статистическая сумма может быть использована для расчёта термодинамических величин, поскольку она имеет очень важный статистический смысл. Вероятность 

Статистическая сумма входит в распределение Гиббса в виде нормировочного множителя (она не зависит от 
Вычисление термодинамической полной энергии[править | править вики-текст]
Чтобы продемонстрировать полезность статистической суммы, рассчитаем термодинамическое значение полной энергии. Это просто математическое ожидание, или среднее по ансамблю значение энергии, равное сумме энергий микросостояний, взятых с весами, равными их вероятностям:
или, что то же самое
Можно также заметить, что если энергии микросостояний зависят от параметра 
для всех 

На этом основан приём, позволяющий вычислить средние значения многих микроскопических величин. Нужно искусственно добавить эту величину к энергии микросостояний (или, на языке квантовой механики, к гамильтониану), вычислить новую статистическую сумму и среднее значение, а затем в итоговом выражении положить 
Связь с термодинамическими величинами[править | править вики-текст]
В этом разделе приведена связь статистической суммы с различными термодинамическими параметрами системы. Эти результаты могут быть получены с помощью метода, описанного в предыдущем разделе, и различных термодинамических соотношений.
Как мы уже видели, энергия равна
Флуктуация энергии равна
Теплоёмкость равна
Энтропия равна
где 



Статистическая сумма подсистем[править | править вики-текст]
Предположим, что система состоит из 

Если подсистемы обладают одинаковыми физическими свойствами, то их статистические суммы одинаковы: 
Из этого правила, однако, есть одно известное исключение. Если подсистемы — это тождественные частицы, то есть, исходя из принципов квантовой механики, их невозможно различить даже в принципе, общая статистическая сумма должна быть разделена на 
Это делается, чтобы не учитывать одно и то же микросостояние несколько раз.
Статистическая сумма большого канонического ансамбля[править | править вики-текст]
Определение[править | править вики-текст]
Аналогично канонической статистической сумме для канонического ансамбля, можно определить большую каноническую статистическую сумму для большого канонического ансамбля — системы, которая может обмениваться со средой и теплотой, и частицами, и имеет постоянную температуру 



где 











Для бозонов числа заполнения могут принимать любые целые неотрицательные значения при том, что их сумма равна 

Частные случаи[править | править вики-текст]
Можно показать, что указанное выражение для большой канонической статистической суммы математически эквивалентно следующему:
(Это произведение иногда берётся по всем значениям энергии, а не по отдельным состояниям, и в этом случае каждая отдельная статистическая сумма должна быть возведена в степень 


Для системы, состоящей из бозонов:
а для системы, состоящей из фермионов:
В случае максвелловско-больцмановского газа необходимо корректно подсчитывать состояния и делить больцмановский множитель 
Связь с термодинамическими величинами[править | править вики-текст]
Так же как и каноническая статистическая сумма, большую каноническую статистическую сумму можно использовать для вычисления термодинамических и статистических величин системы. Как и в каноническом ансамбле, термодинамические величины не фиксированы, а статистически распределены вокруг среднего значения. Обозначая 
Для больцмановских частиц это даёт:
Для бозонов:
Для фермионов:
что совпадает с результатами, получаемыми с помощью канонического ансамбля для статистики Максвелла — Больцмана, статистики Бозе — Эйнштейна и статистики Ферми — Дирака соответственно. (Степень вырождения 

Общее число частиц
Флуктуация общего числа частиц
Внутренняя энергия
Флуктуация внутренней энергии
Давление
Механическое уравнение состояния
Литература[править | править вики-текст]
- Кубо Р. Статистическая механика. — М.: Мир, 1967.
- Хуанг К. Статистическая механика. — М.: Мир, 1966. (Huang, Kerson, «Statistical Mechanics», John Wiley & Sons, New York, 1967.)
- Исихара А. Статистическая физика. — М.: Мир, 1973. (Isihara A. «Statistical Physics». — New York: Academic Press, 1971.)
- Kelly, James J. Lecture notes.
- Ландау, Л. Д., Лифшиц, Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2005. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8..
Статистическая сумма (или статсумма) (обозначается [math]displaystyle{ Z }[/math], от нем. Zustandssumme — сумма по состояниям) — это нормировочный коэффициент в знаменателе соответствующего статистического (вероятностного) распределения, при котором интегральная сумма этого вероятностного распределения (т.е. полная вероятность) по всем возможным состояниям равна 1. Статистическая сумма — важная величина в термодинамике и статистической физике, содержащая информацию о статистических свойствах системы в состоянии термодинамического равновесия. Она может являться функцией температуры и других параметров, таких как объём. Многие термодинамические величины системы, такие как энергия, свободная энергия, энтропия и давление, могут быть выражены через статистическую сумму и её производные.
Статистическая сумма в каноническом ансамбле
Определение
Предположим, что имеется подчиняющаяся законам термодинамики система, находящаяся в постоянном тепловом контакте со средой, которая имеет температуру [math]displaystyle{ T }[/math], а объём системы и количество составляющих её частиц фиксированы. В такой ситуации система относится к каноническому ансамблю. Обозначим точные состояния, в которых может находиться система, через [math]displaystyle{ j }[/math] [math]displaystyle{ (j=1,2,3,ldots) }[/math], а полную энергию системы в состоянии [math]displaystyle{ j }[/math] — [math]displaystyle{ E_j }[/math]. Как правило, эти микросостояния можно рассматривать как дискретные квантовые состояния системы.
Каноническая статистическая сумма — это
- [math]displaystyle{ Z=sum_j e^{-beta E_j}, }[/math]
где обратная температура [math]displaystyle{ beta }[/math] определена как
- [math]displaystyle{ betaequivfrac{1}{k_BT}, }[/math]
а [math]displaystyle{ k_B }[/math] — это постоянная Больцмана.
В классической статистической механике было бы некорректно определять статистическую сумму в виде суммы дискретных членов, как в приведённой выше формуле. В классической механике координаты и импульсы частиц могут меняться непрерывно, и множество микросостояний несчётно. В таком случае необходимо провести разбиение фазового пространства на ячейки, то есть два микросостояния считаются одинаковыми, если их различия в координатах и импульсах «не слишком велики». При этом статистическая сумма принимает вид интеграла. Например, статистическая сумма газа из [math]displaystyle{ N }[/math] классических частиц равна
- [math]displaystyle{ Z=frac{1}{N!h^{3N}}int exp[-beta H(p_1,ldots,p_N,x_1,ldots,x_N)],d^3p_1ldots d^3p_N,d^3x_1ldots d^3x_N, }[/math]
где [math]displaystyle{ h }[/math] — некоторая величина размерности действия (которая должна быть равна постоянной Планка для соответствия квантовой механике), а [math]displaystyle{ H }[/math] — классический гамильтониан. Причины появления множителя [math]displaystyle{ N! }[/math] объяснены ниже. Для простоты в этой статье будет использоваться дискретный вид статистической суммы, но полученные результаты в равной мере относятся и к непрерывному виду.
В квантовой механике статистическая сумма может быть записана более формально как след по пространству состояний (который не зависит от выбора базиса):
- [math]displaystyle{ Z=mathrm{tr},(e^{-beta H}), }[/math]
где [math]displaystyle{ H }[/math] — оператор Гамильтона. Экспонента от оператора определяется с помощью разложения в степенной ряд.
Смысл и значимость
Сначала рассмотрим, от чего она зависит. Статистическая сумма является функцией температуры [math]displaystyle{ T }[/math], а также энергий микросостояний [math]displaystyle{ E_1,E_2,E_3 }[/math] и т. д. Энергии микросостояний определяются другими термодинамическими величинами, такими как число частиц и объём, а также микроскопическими свойствами, такими как масса частиц. Эта зависимость от микроскопических свойств является основной в статистической механике. По модели микроскопических составляющих системы можно рассчитать энергии микросостояний, а следовательно, и статистическую сумму, которая позволяет рассчитать все остальные термодинамические свойства системы.
Статистическая сумма может быть использована для расчёта термодинамических величин, поскольку она имеет очень важный статистический смысл. Вероятность [math]displaystyle{ P_j }[/math], с которой система находится в микросостоянии [math]displaystyle{ j }[/math], равна
- [math]displaystyle{ P_j=frac{1}{Z}e^{-beta E_j}. }[/math]
Статистическая сумма входит в распределение Гиббса в виде нормировочного множителя (она не зависит от [math]displaystyle{ j }[/math]), обеспечивая равенство единице суммы вероятностей:
- [math]displaystyle{ sum_j P_j=frac{1}{Z}sum_j e^{-beta E_j}=frac{1}{Z}Z=1. }[/math]
Вычисление термодинамической полной энергии
Чтобы продемонстрировать полезность статистической суммы, рассчитаем термодинамическое значение полной энергии. Это просто математическое ожидание, или среднее по ансамблю значение энергии, равное сумме энергий микросостояний, взятых с весами, равными их вероятностям:
- [math]displaystyle{ langle Erangle=sum_j E_jP_j=frac{1}{Z}sum_j E_j e^{-beta E_j}=-frac{1}{Z}frac{partial}{partialbeta}Z(beta,;E_1,;E_2,;ldots)=-frac{partialln Z}{partialbeta} }[/math]
или, что то же самое
- [math]displaystyle{ langle Erangle=k_B T^2frac{partialln Z}{partial T}. }[/math]
Можно также заметить, что если энергии микросостояний зависят от параметра [math]displaystyle{ lambda }[/math] как
- [math]displaystyle{ E_j=E_j^{(0)}+lambda A_j }[/math]
для всех [math]displaystyle{ j }[/math], то среднее значение [math]displaystyle{ A }[/math] равно
- [math]displaystyle{ langle Arangle=sum_j A_jP_j=-frac{1}{beta}frac{partial}{partiallambda}ln Z(beta,;lambda). }[/math]
На этом основан приём, позволяющий вычислить средние значения многих микроскопических величин. Нужно искусственно добавить эту величину к энергии микросостояний (или, на языке квантовой механики, к гамильтониану), вычислить новую статистическую сумму и среднее значение, а затем в итоговом выражении положить [math]displaystyle{ lambda }[/math] равным нулю. Аналогичный метод применяется в квантовой теории поля.
Связь с термодинамическими величинами
В этом разделе приведена связь статистической суммы с различными термодинамическими параметрами системы. Эти результаты могут быть получены с помощью метода, описанного в предыдущем разделе, и различных термодинамических соотношений.
Как мы уже видели, энергия равна
- [math]displaystyle{ langle Erangle=-frac{partialln Z}{partialbeta}. }[/math]
Флуктуация энергии равна
- [math]displaystyle{ langledelta E^2rangleequivlangle(E-langle Erangle)^2rangle=frac{partial^2ln Z}{partialbeta^2}. }[/math]
Теплоёмкость равна
- [math]displaystyle{ c_v=frac{partiallangle Erangle}{partial T}=frac{1}{k_B T^2}langledelta E^2rangle. }[/math]
Энтропия равна
- [math]displaystyle{ Sequiv-k_Bsum_j P_jln P_j=k_B(ln Z+betalangle Erangle)=frac{partial}{partial T}(k_B Tln Z)=-frac{partial F}{partial T}, }[/math]
где [math]displaystyle{ F }[/math] — свободная энергия, определяемая как [math]displaystyle{ F=E-TS }[/math], где [math]displaystyle{ E }[/math] — полная энергия, а [math]displaystyle{ S }[/math] — энтропия, так что
- [math]displaystyle{ F=langle Erangle-TS=-k_B Tln Z. }[/math]
Статистическая сумма подсистем
Предположим, что система состоит из [math]displaystyle{ N }[/math] подсистем, взаимодействие между которыми пренебрежимо мало. Если статистические суммы подсистем равны [math]displaystyle{ zeta_1,;zeta_2,;ldots,;zeta_N }[/math], то статистическая сумма всей системы равна произведению отдельных статистических сумм:
- [math]displaystyle{ Z =prod_{j=1}^Nzeta_j. }[/math]
Если подсистемы обладают одинаковыми физическими свойствами, то их статистические суммы одинаковы: [math]displaystyle{ zeta_1=zeta_2=ldots=zeta }[/math], и в этом случае
- [math]displaystyle{ Z=zeta^N. }[/math]
Из этого правила, однако, есть одно известное исключение. Если подсистемы — это тождественные частицы, то есть, исходя из принципов квантовой механики, их невозможно различить даже в принципе, общая статистическая сумма должна быть разделена на [math]displaystyle{ N! }[/math]:
- [math]displaystyle{ Z=frac{zeta^N}{N!}. }[/math]
Это делается, чтобы не учитывать одно и то же микросостояние несколько раз.
Статистическая сумма большого канонического ансамбля
Определение
Аналогично канонической статистической сумме для канонического ансамбля, можно определить большую каноническую статистическую сумму для большого канонического ансамбля — системы, которая может обмениваться со средой и теплотой, и частицами, и имеет постоянную температуру [math]displaystyle{ T }[/math], объём [math]displaystyle{ V }[/math] и химический потенциал [math]displaystyle{ mu }[/math]. Большая каноническая статистическая сумма, хотя и более сложна для понимания, упрощает расчёт квантовых систем. Большая каноническая статистическая сумма [math]displaystyle{ mathcal{Z} }[/math] для квантового идеального газа записывается как:
- [math]displaystyle{ mathcal{Z}=sum_{N=0}^infty,sum_{{n_i}},prod_i e^{-beta n_i(varepsilon_i-mu)}, }[/math]
где [math]displaystyle{ N }[/math] — общее количество частиц в объёме [math]displaystyle{ V }[/math], индекс [math]displaystyle{ i }[/math] пробегает все микросостояния системы, [math]displaystyle{ n_i }[/math] — число частиц в состоянии [math]displaystyle{ i }[/math], а [math]displaystyle{ varepsilon_i }[/math] — энергия в состоянии [math]displaystyle{ i }[/math]. [math]displaystyle{ {n_i} }[/math] — всевозможные наборы чисел заполнения каждого микросостояния, такие что [math]displaystyle{ sum_i n_i=N }[/math].
Рассмотрим, например, слагаемое, соответствующее [math]displaystyle{ N=3 }[/math]. Один из возможных наборов чисел заполнения будет [math]displaystyle{ {n_i}=0,;1,;0,;2,;0,ldots }[/math], он даёт вклад в слагаемое с [math]displaystyle{ N=3 }[/math], равный
- [math]displaystyle{ prod_i e^{-beta n_i(varepsilon_i-mu)}=e^{-beta(varepsilon_1-mu)},e^{-2beta(varepsilon_3-mu)}. }[/math]
Для бозонов числа заполнения могут принимать любые целые неотрицательные значения при том, что их сумма равна [math]displaystyle{ N }[/math]. Для фермионов, в соответствии с принципом запрета Паули, числа заполнения могут быть равны только 0 или 1, но их сумма опять же равна [math]displaystyle{ N }[/math].
Частные случаи
Можно показать, что указанное выражение для большой канонической статистической суммы математически эквивалентно следующему:
- [math]displaystyle{ mathcal{Z}=prod_imathcal{Z}_i. }[/math]
(Это произведение иногда берётся по всем значениям энергии, а не по отдельным состояниям, и в этом случае каждая отдельная статистическая сумма должна быть возведена в степень [math]displaystyle{ g_i }[/math], где [math]displaystyle{ g_i }[/math] — число состояний с такой энергией. [math]displaystyle{ g_i }[/math] также называется степенью вырождения.)
Для системы, состоящей из бозонов:
- [math]displaystyle{ mathcal{Z}_i=sum_{n_i=0}^infty e^{-beta n_i(varepsilon_i-mu)}=frac{1}{1-e^{-beta(varepsilon_i-mu)}}, }[/math]
а для системы, состоящей из фермионов:
- [math]displaystyle{ mathcal{Z}_i=sum_{n_i=0}^1 e^{-beta n_i(varepsilon_i-mu)}=1+e^{-beta(varepsilon_i-mu)}. }[/math]
В случае максвелловско-больцмановского газа необходимо корректно подсчитывать состояния и делить больцмановский множитель [math]displaystyle{ e^{-beta (varepsilon_i-mu)} }[/math] на [math]displaystyle{ n_i! }[/math]
- [math]displaystyle{ mathcal{Z}_i=sum_{n_i=0}^inftyfrac{e^{-beta n_i(varepsilon_i-mu)}}{n_i!}=expleft(e^{-beta(varepsilon_i-mu)}right). }[/math]
Связь с термодинамическими величинами
Так же как и каноническая статистическая сумма, большую каноническую статистическую сумму можно использовать для вычисления термодинамических и статистических величин системы. Как и в каноническом ансамбле, термодинамические величины не фиксированы, а статистически распределены вокруг среднего значения.
Обозначая [math]displaystyle{ alpha=-betamu }[/math], получаем средние значения чисел заполнения:
- [math]displaystyle{ langle n_irangle=-left(frac{partiallnmathcal{Z}_i}{partialalpha}right)_{beta,;V}=frac{1}{beta}left(frac{partiallnmathcal{Z}_i}{partialmu}right)_{beta,;V}. }[/math]
Для больцмановских частиц это даёт:
- [math]displaystyle{ langle n_irangle=e^{-beta(varepsilon_i-mu)}. }[/math]
Для бозонов:
- [math]displaystyle{ langle n_irangle=frac{1}{e^{beta(varepsilon_i-mu)}-1}. }[/math]
Для фермионов:
- [math]displaystyle{ langle n_irangle=frac{1}{e^{beta(varepsilon_i-mu)}+1}, }[/math]
что совпадает с результатами, получаемыми с помощью канонического ансамбля для статистики Максвелла — Больцмана, статистики Бозе — Эйнштейна и статистики Ферми — Дирака соответственно. (Степень вырождения [math]displaystyle{ g_i }[/math] отсутствует в этих уравнениях, поскольку индекс [math]displaystyle{ i }[/math] нумерует отдельные состояния, а не уровни энергии.)
Общее число частиц
- [math]displaystyle{ langle Nrangle=-left(frac{partiallnmathcal{Z}}{partialalpha}right)_{beta,;V}=frac{1}{beta}left(frac{partiallnmathcal{Z}}{partialmu}right)_{beta,;V}. }[/math]
Флуктуация общего числа частиц
- [math]displaystyle{ mathrm{var},(N)=left(frac{partial^2lnmathcal{Z}}{partialalpha^2}right)_{beta,;V}. }[/math]
Внутренняя энергия
- [math]displaystyle{ langle Erangle=-left(frac{partiallnmathcal{Z}}{partialbeta}right)_{mu,;V}+mulangle Nrangle. }[/math]
Флуктуация внутренней энергии
- [math]displaystyle{ mathrm{var},(E)=left(frac{partial^2lnmathcal{Z}}{partialbeta^2}right)_{mu,;V}. }[/math]
Давление
- [math]displaystyle{ langle Prangle=frac{1}{beta}left(frac{partiallnmathcal{Z}}{partial V}right)_{mu,;beta}. }[/math]
Механическое уравнение состояния
- [math]displaystyle{ langle PVrangle=frac{lnmathcal{Z}}{beta}. }[/math]
Литература
- Кубо Р. Статистическая механика. — М.: Мир, 1967.
- Хуанг К. Статистическая механика. — М.: Мир, 1966. (Huang, Kerson, «Statistical Mechanics», John Wiley & Sons, New York, 1967.)
- Исихара А. Статистическая физика. — М.: Мир, 1973. (Isihara A. «Statistical Physics». — New York: Academic Press, 1971.)
- Kelly, James J. Lecture notes.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2005. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8..
Статистическая сумма (или статсумма) (обозначается Z {displaystyle Z} , от нем. Zustandssumme — сумма по состояниям) — это нормировочный коэффициент в знаменателе соответствующего статистического (вероятностного) распределения, при котором интегральная сумма этого вероятностного распределения (т.е. полная вероятность) по всем возможным состояниям равна 1. Статистическая сумма — важная величина в термодинамике и статистической физике, содержащая информацию о статистических свойствах системы в состоянии термодинамического равновесия. Она может являться функцией температуры и других параметров, таких как объём. Многие термодинамические величины системы, такие как энергия, свободная энергия, энтропия и давление, могут быть выражены через статистическую сумму и её производные.
Статистическая сумма в каноническом ансамбле
Определение
Предположим, что имеется подчиняющаяся законам термодинамики система, находящаяся в постоянном тепловом контакте со средой, которая имеет температуру T {displaystyle T} , а объём системы и количество составляющих её частиц фиксированы. В такой ситуации система относится к каноническому ансамблю. Обозначим точные состояния, в которых может находиться система, через j {displaystyle j} ( j = 1 , 2 , 3 , … ) {displaystyle (j=1,2,3,ldots )} , а полную энергию системы в состоянии j {displaystyle j} — E j {displaystyle E_{j}} . Как правило, эти микросостояния можно рассматривать как дискретные квантовые состояния системы.
Каноническая статистическая сумма — это
Z = ∑ j e − β E j , {displaystyle Z=sum _{j}e^{-eta E_{j}},}
где обратная температура β {displaystyle eta } определена как
β ≡ 1 k B T , {displaystyle eta equiv {frac {1}{k_{B}T}},}
а k B {displaystyle k_{B}} — это постоянная Больцмана. В классической статистической механике было бы некорректно определять статистическую сумму в виде суммы дискретных членов, как в приведённой выше формуле. В классической механике координаты и импульсы частиц могут меняться непрерывно, и множество микросостояний несчётно. В таком случае необходимо провести разбиение фазового пространства на ячейки, то есть два микросостояния считаются одинаковыми, если их различия в координатах и импульсах «не слишком велики». При этом статистическая сумма принимает вид интеграла. Например, статистическая сумма газа из N {displaystyle N} классических частиц равна
Z = 1 N ! h 3 N ∫ exp [ − β H ( p 1 , … , p N , x 1 , … , x N ) ] d 3 p 1 … d 3 p N d 3 x 1 … d 3 x N , {displaystyle Z={frac {1}{N!h^{3N}}}int exp[-eta H(p_{1},ldots ,p_{N},x_{1},ldots ,x_{N})],d^{3}p_{1}ldots d^{3}p_{N},d^{3}x_{1}ldots d^{3}x_{N},}
где h {displaystyle h} — некоторая величина размерности действия (которая должна быть равна постоянной Планка для соответствия квантовой механике), а H {displaystyle H} — классический гамильтониан. Причины появления множителя N ! {displaystyle N!} объяснены ниже. Для простоты в этой статье будет использоваться дискретный вид статистической суммы, но полученные результаты в равной мере относятся и к непрерывному виду.
В квантовой механике статистическая сумма может быть записана более формально как след по пространству состояний (который не зависит от выбора базиса):
Z = t r ( e − β H ) , {displaystyle Z=mathrm {tr} ,(e^{-eta H}),}
где H {displaystyle H} — оператор Гамильтона. Экспонента от оператора определяется с помощью разложения в степенной ряд.
Смысл и значимость
Сначала рассмотрим, от чего она зависит. Статистическая сумма является функцией температуры T {displaystyle T} , а также энергий микросостояний E 1 , E 2 , E 3 {displaystyle E_{1},E_{2},E_{3}} и т. д. Энергии микросостояний определяются другими термодинамическими величинами, такими как число частиц и объём, а также микроскопическими свойствами, такими как масса частиц. Эта зависимость от микроскопических свойств является основной в статистической механике. По модели микроскопических составляющих системы можно рассчитать энергии микросостояний, а следовательно, и статистическую сумму, которая позволяет рассчитать все остальные термодинамические свойства системы.
Статистическая сумма может быть использована для расчёта термодинамических величин, поскольку она имеет очень важный статистический смысл. Вероятность P j {displaystyle P_{j}} , с которой система находится в микросостоянии j {displaystyle j} , равна
P j = 1 Z e − β E j . {displaystyle P_{j}={frac {1}{Z}}e^{-eta E_{j}}.}
Статистическая сумма входит в распределение Гиббса в виде нормировочного множителя (она не зависит от j {displaystyle j} ), обеспечивая равенство единице суммы вероятностей:
∑ j P j = 1 Z ∑ j e − β E j = 1 Z Z = 1. {displaystyle sum _{j}P_{j}={frac {1}{Z}}sum _{j}e^{-eta E_{j}}={frac {1}{Z}}Z=1.}
Вычисление термодинамической полной энергии
Чтобы продемонстрировать полезность статистической суммы, рассчитаем термодинамическое значение полной энергии. Это просто математическое ожидание, или среднее по ансамблю значение энергии, равное сумме энергий микросостояний, взятых с весами, равными их вероятностям:
⟨ E ⟩ = ∑ j E j P j = 1 Z ∑ j E j e − β E j = − 1 Z ∂ ∂ β Z ( β , E 1 , E 2 , … ) = − ∂ ln Z ∂ β {displaystyle langle E
angle =sum _{j}E_{j}P_{j}={frac {1}{Z}}sum _{j}E_{j}e^{-eta E_{j}}=-{frac {1}{Z}}{frac {partial }{partial eta }}Z(eta ,;E_{1},;E_{2},;ldots )=-{frac {partial ln Z}{partial eta }}}
или, что то же самое
⟨ E ⟩ = k B T 2 ∂ ln Z ∂ T . {displaystyle langle E
angle =k_{B}T^{2}{frac {partial ln Z}{partial T}}.}
Можно также заметить, что если энергии микросостояний зависят от параметра λ {displaystyle lambda } как
E j = E j ( 0 ) + λ A j {displaystyle E_{j}=E_{j}^{(0)}+lambda A_{j}}
для всех j {displaystyle j} , то среднее значение A {displaystyle A} равно
⟨ A ⟩ = ∑ j A j P j = − 1 β ∂ ∂ λ ln Z ( β , λ ) . {displaystyle langle A
angle =sum _{j}A_{j}P_{j}=-{frac {1}{eta }}{frac {partial }{partial lambda }}ln Z(eta ,;lambda ).}
На этом основан приём, позволяющий вычислить средние значения многих микроскопических величин. Нужно искусственно добавить эту величину к энергии микросостояний (или, на языке квантовой механики, к гамильтониану), вычислить новую статистическую сумму и среднее значение, а затем в итоговом выражении положить λ {displaystyle lambda } равным нулю. Аналогичный метод применяется в квантовой теории поля.
Связь с термодинамическими величинами
В этом разделе приведена связь статистической суммы с различными термодинамическими параметрами системы. Эти результаты могут быть получены с помощью метода, описанного в предыдущем разделе, и различных термодинамических соотношений.
Как мы уже видели, энергия равна
⟨ E ⟩ = − ∂ ln Z ∂ β . {displaystyle langle E
angle =-{frac {partial ln Z}{partial eta }}.}
Флуктуация энергии равна
⟨ δ E 2 ⟩ ≡ ⟨ ( E − ⟨ E ⟩ ) 2 ⟩ = ∂ 2 ln Z ∂ β 2 . {displaystyle langle delta E^{2}
angle equiv langle (E-langle E
angle )^{2}
angle ={frac {partial ^{2}ln Z}{partial eta ^{2}}}.}
Теплоёмкость равна
c v = ∂ ⟨ E ⟩ ∂ T = 1 k B T 2 ⟨ δ E 2 ⟩ . {displaystyle c_{v}={frac {partial langle E
angle }{partial T}}={frac {1}{k_{B}T^{2}}}langle delta E^{2}
angle .}
Энтропия равна
S ≡ − k B ∑ j P j ln P j = k B ( ln Z + β ⟨ E ⟩ ) = ∂ ∂ T ( k B T ln Z ) = − ∂ F ∂ T , {displaystyle Sequiv -k_{B}sum _{j}P_{j}ln P_{j}=k_{B}(ln Z+eta langle E
angle )={frac {partial }{partial T}}(k_{B}Tln Z)=-{frac {partial F}{partial T}},}
где F {displaystyle F} — свободная энергия, определяемая как F = E − T S {displaystyle F=E-TS} , где E {displaystyle E} — полная энергия, а S {displaystyle S} — энтропия, так что
F = ⟨ E ⟩ − T S = − k B T ln Z . {displaystyle F=langle E
angle -TS=-k_{B}Tln Z.}
Статистическая сумма подсистем
Предположим, что система состоит из N {displaystyle N} подсистем, взаимодействие между которыми пренебрежимо мало. Если статистические суммы подсистем равны ζ 1 , ζ 2 , … , ζ N {displaystyle zeta _{1},;zeta _{2},;ldots ,;zeta _{N}} , то статистическая сумма всей системы равна произведению отдельных статистических сумм:
Z = ∏ j = 1 N ζ j . {displaystyle Z=prod _{j=1}^{N}zeta _{j}.}
Если подсистемы обладают одинаковыми физическими свойствами, то их статистические суммы одинаковы: ζ 1 = ζ 2 = … = ζ {displaystyle zeta _{1}=zeta _{2}=ldots =zeta } , и в этом случае
Z = ζ N . {displaystyle Z=zeta ^{N}.}
Из этого правила, однако, есть одно известное исключение. Если подсистемы — это тождественные частицы, то есть, исходя из принципов квантовой механики, их невозможно различить даже в принципе, общая статистическая сумма должна быть разделена на N ! {displaystyle N!} :
Z = ζ N N ! . {displaystyle Z={frac {zeta ^{N}}{N!}}.}
Это делается, чтобы не учитывать одно и то же микросостояние несколько раз.
Статистическая сумма большого канонического ансамбля
Определение
Аналогично канонической статистической сумме для канонического ансамбля, можно определить большую каноническую статистическую сумму для большого канонического ансамбля — системы, которая может обмениваться со средой и теплотой, и частицами, и имеет постоянную температуру T {displaystyle T} , объём V {displaystyle V} и химический потенциал μ {displaystyle mu } . Большая каноническая статистическая сумма, хотя и более сложна для понимания, упрощает расчёт квантовых систем. Большая каноническая статистическая сумма Z {displaystyle {mathcal {Z}}} для квантового идеального газа записывается как:
Z = ∑ N = 0 ∞ ∑ { n i } ∏ i e − β n i ( ε i − μ ) , {displaystyle {mathcal {Z}}=sum _{N=0}^{infty },sum _{{n_{i}}},prod _{i}e^{-eta n_{i}(varepsilon _{i}-mu )},}
где N {displaystyle N} — общее количество частиц в объёме V {displaystyle V} , индекс i {displaystyle i} пробегает все микросостояния системы, n i {displaystyle n_{i}} — число частиц в состоянии i {displaystyle i} , а ε i {displaystyle varepsilon _{i}} — энергия в состоянии i {displaystyle i} . { n i } {displaystyle {n_{i}}} — всевозможные наборы чисел заполнения каждого микросостояния, такие что ∑ i n i = N {displaystyle sum _{i}n_{i}=N} . Рассмотрим, например, слагаемое, соответствующее N = 3 {displaystyle N=3} . Один из возможных наборов чисел заполнения будет { n i } = 0 , 1 , 0 , 2 , 0 , … {displaystyle {n_{i}}=0,;1,;0,;2,;0,ldots } , он даёт вклад в слагаемое с N = 3 {displaystyle N=3} , равный
∏ i e − β n i ( ε i − μ ) = e − β ( ε 1 − μ ) e − 2 β ( ε 3 − μ ) . {displaystyle prod _{i}e^{-eta n_{i}(varepsilon _{i}-mu )}=e^{-eta (varepsilon _{1}-mu )},e^{-2eta (varepsilon _{3}-mu )}.}
Для бозонов числа заполнения могут принимать любые целые неотрицательные значения при том, что их сумма равна N {displaystyle N} . Для фермионов, в соответствии с принципом запрета Паули, числа заполнения могут быть равны только 0 или 1, но их сумма опять же равна N {displaystyle N} .
Частные случаи
Можно показать, что указанное выражение для большой канонической статистической суммы математически эквивалентно следующему:
Z = ∏ i Z i . {displaystyle {mathcal {Z}}=prod _{i}{mathcal {Z}}_{i}.}
(Это произведение иногда берётся по всем значениям энергии, а не по отдельным состояниям, и в этом случае каждая отдельная статистическая сумма должна быть возведена в степень g i {displaystyle g_{i}} , где g i {displaystyle g_{i}} — число состояний с такой энергией. g i {displaystyle g_{i}} также называется степенью вырождения.)
Для системы, состоящей из бозонов:
Z i = ∑ n i = 0 ∞ e − β n i ( ε i − μ ) = 1 1 − e − β ( ε i − μ ) , {displaystyle {mathcal {Z}}_{i}=sum _{n_{i}=0}^{infty }e^{-eta n_{i}(varepsilon _{i}-mu )}={frac {1}{1-e^{-eta (varepsilon _{i}-mu )}}},}
а для системы, состоящей из фермионов:
Z i = ∑ n i = 0 1 e − β n i ( ε i − μ ) = 1 + e − β ( ε i − μ ) . {displaystyle {mathcal {Z}}_{i}=sum _{n_{i}=0}^{1}e^{-eta n_{i}(varepsilon _{i}-mu )}=1+e^{-eta (varepsilon _{i}-mu )}.}
В случае максвелловско-больцмановского газа необходимо корректно подсчитывать состояния и делить больцмановский множитель e − β ( ε i − μ ) {displaystyle e^{-eta (varepsilon _{i}-mu )}} на n i ! {displaystyle n_{i}!}
Z i = ∑ n i = 0 ∞ e − β n i ( ε i − μ ) n i ! = exp ( e − β ( ε i − μ ) ) . {displaystyle {mathcal {Z}}_{i}=sum _{n_{i}=0}^{infty }{frac {e^{-eta n_{i}(varepsilon _{i}-mu )}}{n_{i}!}}=exp left(e^{-eta (varepsilon _{i}-mu )}
ight).}
Связь с термодинамическими величинами
Так же как и каноническая статистическая сумма, большую каноническую статистическую сумму можно использовать для вычисления термодинамических и статистических величин системы. Как и в каноническом ансамбле, термодинамические величины не фиксированы, а статистически распределены вокруг среднего значения. Обозначая α = − β μ {displaystyle alpha =-eta mu } , получаем средние значения чисел заполнения:
⟨ n i ⟩ = − ( ∂ ln Z i ∂ α ) β , V = 1 β ( ∂ ln Z i ∂ μ ) β , V . {displaystyle langle n_{i}
angle =-left({frac {partial ln {mathcal {Z}}_{i}}{partial alpha }}
ight)_{eta ,;V}={frac {1}{eta }}left({frac {partial ln {mathcal {Z}}_{i}}{partial mu }}
ight)_{eta ,;V}.}
Для больцмановских частиц это даёт:
⟨ n i ⟩ = e − β ( ε i − μ ) . {displaystyle langle n_{i}
angle =e^{-eta (varepsilon _{i}-mu )}.}
Для бозонов:
⟨ n i ⟩ = 1 e β ( ε i − μ ) − 1 . {displaystyle langle n_{i}
angle ={frac {1}{e^{eta (varepsilon _{i}-mu )}-1}}.}
Для фермионов:
⟨ n i ⟩ = 1 e β ( ε i − μ ) + 1 , {displaystyle langle n_{i}
angle ={frac {1}{e^{eta (varepsilon _{i}-mu )}+1}},}
что совпадает с результатами, получаемыми с помощью канонического ансамбля для статистики Максвелла — Больцмана, статистики Бозе — Эйнштейна и статистики Ферми — Дирака соответственно. (Степень вырождения g i {displaystyle g_{i}} отсутствует в этих уравнениях, поскольку индекс i {displaystyle i} нумерует отдельные состояния, а не уровни энергии.)
Общее число частиц
⟨ N ⟩ = − ( ∂ ln Z ∂ α ) β , V = 1 β ( ∂ ln Z ∂ μ ) β , V . {displaystyle langle N
angle =-left({frac {partial ln {mathcal {Z}}}{partial alpha }}
ight)_{eta ,;V}={frac {1}{eta }}left({frac {partial ln {mathcal {Z}}}{partial mu }}
ight)_{eta ,;V}.}
Флуктуация общего числа частиц
v a r ( N ) = ( ∂ 2 ln Z ∂ α 2 ) β , V . {displaystyle mathrm {var} ,(N)=left({frac {partial ^{2}ln {mathcal {Z}}}{partial alpha ^{2}}}
ight)_{eta ,;V}.}
Внутренняя энергия
⟨ E ⟩ = − ( ∂ ln Z ∂ β ) μ , V + μ ⟨ N ⟩ . {displaystyle langle E
angle =-left({frac {partial ln {mathcal {Z}}}{partial eta }}
ight)_{mu ,;V}+mu langle N
angle .}
Флуктуация внутренней энергии
v a r ( E ) = ( ∂ 2 ln Z ∂ β 2 ) μ , V . {displaystyle mathrm {var} ,(E)=left({frac {partial ^{2}ln {mathcal {Z}}}{partial eta ^{2}}}
ight)_{mu ,;V}.}
Давление
⟨ P ⟩ = 1 β ( ∂ ln Z ∂ V ) μ , β . {displaystyle langle P
angle ={frac {1}{eta }}left({frac {partial ln {mathcal {Z}}}{partial V}}
ight)_{mu ,;eta }.}
Механическое уравнение состояния
⟨ P V ⟩ = ln Z β . {displaystyle langle PV
angle ={frac {ln {mathcal {Z}}}{eta }}.}



![{displaystyle Z={frac {1}{N!h^{3N}}}int ,exp[-beta H(p_{1}cdots p_{N},x_{1}cdots x_{N})];d^{3}p_{1}cdots d^{3}p_{N},d^{3}x_{1}cdots d^{3}x_{N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a98d468eeb29f3214910271c6ad383d7f48f9fa)














































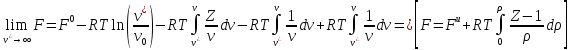
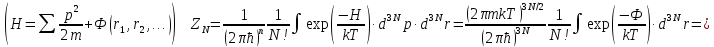
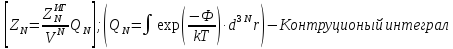






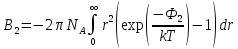
















![Z=frac{1}{N!h^{3N}}int exp[-beta H(p_1,ldots,p_N,x_1,ldots,x_N)],d^3p_1ldots d^3p_N,d^3x_1ldots d^3x_N,](https://web.archive.org/web/20151110050105im_/https://upload.wikimedia.org/math/7/0/5/7056bcbab7abd4c996ee9dba8888c9a8.png)































