Как найти ставку потоварного налога - Исправление недочетов и поиск решений вместе с Examum.ru

Потоварный налог — налог, представляющий собой фиксированную сумму, взимаемую с единицы продукции.

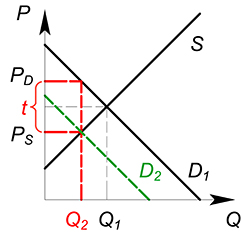
Рассмотрим некий рынок (возьмем для примера совершенно конкурентный). Раньше, до вмешательства государства, на данном рынке продавалось некоторое количество продукции $Q^*$ по цене $P^*$. Сумму, которую потребители уплачивали за единицу продукции, полностью получали производители. Цена покупки $P_D$ была равна цене продажи $P_S$.

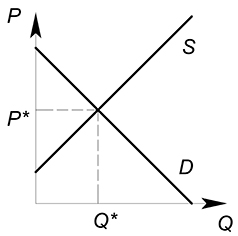
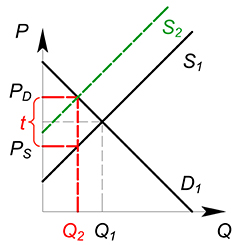
Представим, что государство ввело на данном рынке потоварный налог по ставке $t$. Теперь фирма должна, получив от покупателя сумму $P_D$ за единицу продукции, отдать государству часть этой суммы, равную ставке налога $t$. В новых условиях фирма получает сумму $P_D-t$ за единицу товара. Фактически для фирмы уменьшилась цена, по которой она продает свой продукт. $P_S=P_D-t$. При введении налога количество покупаемого и продаваемого товара уменьшается.

Действие, которое оказывает налог на ситуацию на рынке, эквивалентно снижению спроса или увеличению издержек. Налог, наложенный на покупателя, окажет такое же влияние на рынок, что и налог, наложенный на производителя.

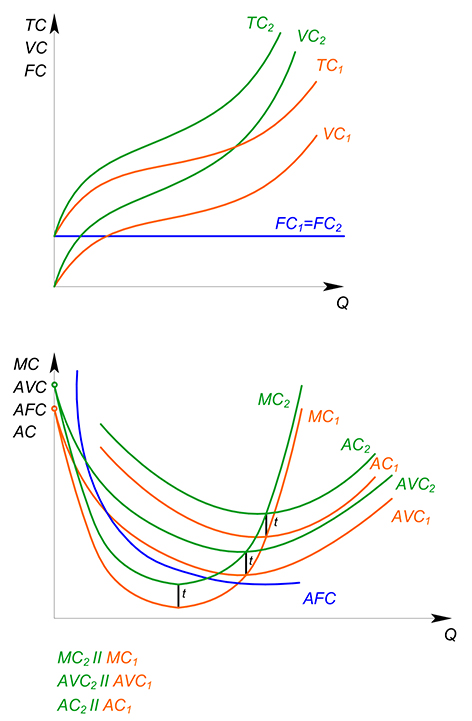
Рассмотрим, какое действие оказывает налог на функции издержек одной фирмы:

$TC(Q)_2=TC(Q)_1+tQ$

Пример 1
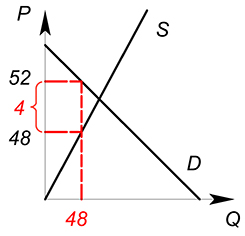
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство вводит налог по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Решать такую задачу удобно, составив следующую систему уравнений:

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S+4
end {cases}$

Отсюда получаем:

$100-(P_S+4)=P_S$

$P_S=48$

$P_D=48+4=52$

$Q_D=Q_S=48$

Пример 2
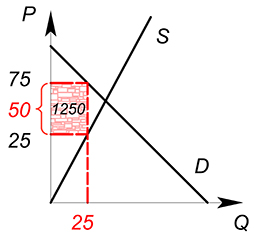
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство хочет максимизировать сумму налоговых поступлений. Найдите $Q^*$, $P_D$, $P_S$, оптимальную ставку налога, сумму налоговых поступлений, построить кривую Лаффера

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S+t
end {cases}$

$100-P_S-t=P_S$

$P_S=dfrac{100-t}{2}$

$Q_S=P_S=dfrac{100-t}{2}$

Сумма налоговых поступлений будет равна ставке налога, умноженной на количество проданного товара:

$T=tcdot Q^*$

$T(t)=tcdot Q(t)$

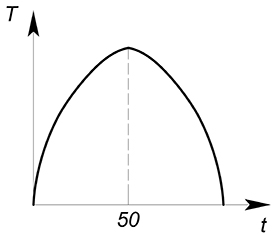
$T(t)=tcdot (dfrac{100-t}{2})=50t-0{,}5t^2$

Данная функция, описывающая зависимость суммы налоговых поступлений от ставки налога, называется кривой Лаффера.

Максимизируем данную функцию:

$T'(t)=50-t$

$t^*=50$

$T»(t)=-1<0$, максимум

Теперь изобразим ее:

$Q_D=Q_S=25$

$P_D=75$

$P_S=25$

$T=50cdot 25=1250$

Пример 3

Принцип введения налога на монополизированном рынке такой же как и на совершенно конкурентном.

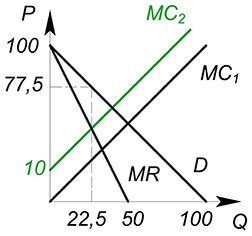
$P_D(Q)=100-Q$, $TC(Q)=Q^2+10$, $t=510$, найти прибыль фирмы после введения налога

Введем налог на продавца. Он увеличивает издержки фирмы:

$TC(Q)_2=TC(Q)_1+tQ=Q^2+10Q+10$

$pi(Q)=100Q-Q^2-Q^2-10Q-10=90Q-2Q^2-10$

$pi'(Q)=90-4Q=0$

$Q^*=22{,}5$

$pi(Q)=1002{,}5>0$, фирма остается на рынке

Пример 4

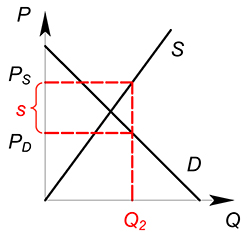
Действие потоварной субсидии обратно действию потоварного налога.

Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение — $Q_S=P_S$, государство вводит субсидию по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Покупатель платит за единицу товара $P_D$ меньшую $P_S=P_D+s$

$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S-4
end {cases}$

$100-P_S+s=P_S$

$P_S=52$

$P_D=48$

$Q_S=Q_D=52$

Источник

Лекция: налогообложение

В результате
введения налогов и субсидий появляются
стимулы для увеличения
(уменьшения) производства и /или
потребления.

Рассмотрим влияние
различных видов налогов на рыночное
равновесие.

Аккордный
(паушальный) —
налог, взимаемый в виде фиксированной
суммы (Тх=соnst).
Пример — плата за лицензию.

Количественный
— налог,
сумма которого зависит от размера
налогооблагаемой базы (стоимостной,
физической или иной характеристики
объекта налогообложения). Внутри данной
группы налогов нас будут интересовать
два вида: потоварный и стоимостной.

Потоварный —
налог, сумма которого зависит от размера
выпуска. Налоговая ставка (t)
указывает, какая сумма должна быть
уплачена государству с каждой единицы
объема продаж. Общая сумма налоговых
сборов равна: Тх
= tQ. Пример —
специфические акцизы (акцизы с твердыми
налоговыми ставками в виде абсолютной
суммы на единицу измерения, например,
акцизы на спиртосодержащую продукцию,
бензин и автомобили в России).

Стоимостной
— налог, сумма которого зависит от
стоимости реализации. Налоговая ставка
(t) указывает, какая доля стоимости
реализации должна быть уплачена
государству в виде налога.

Общая сумма налоговых
сборов равна: Тх
= t∙[РQ].
Однако данное выражение может быть
записано в другом виде: Тх=[tР]∙Q.
В этом_случае налоговую ставку (t)
можно интерпретировать как долю цены
реализации, которая должна быть уплачена
государству виде налога с каждой
проданной единицы товара.

Внутри данной
группы налога также выделяют два вида
в зависимости от того, цена потребителя
(Рd) или производителя (Рs)
используется при расчете стоимости
реализации. Примером первого варианта
могут служить адвалорные акцизы, второго
— НДС и налог с продаж.

Рассмотрим более
подробно последствия применения
потоварного налога, НДС и адвалорного
акциза. Прежде всего, остановимся на
общих положениях, касающихся всех видов
рассматриваемых налогов.

Во-первых, все они
приводят к тому, что после налогообложения
цена,
уплачиваемая за товар потребителем,
оказывается выше цены, которую получает
производитель.
Действительно, если налог платит
производитель, то после расчета с
покупателем он должен часть цены товара
перечислить в виде налога государству,
то есть продавец получит меньше, чем
заплатил потребитель.

Если же налог
оплачивает покупатель, то после расчета
с продавцом, он обязан еще некоторую
сумму перечислить в виде налога, в итоге
заплатив больше, чем получил производитель.
Различия же трех видов налогов касаются
только того, на сколько отличаются
указанные величины.

Последствия применения потоварного налога

Пусть первоначально
рынок товара находится в равновесии.
Если первоначальная кривая спроса имела
вид:

,
а кривая предложения:

,
то в таком случае равновесие до применения
налога соответствовало решению следующей
системы уравнений:

(1)

На графике равновесие
установится в точке пересечения кривых
спроса и предложения —
.
Равновесный объем составит

единиц товара, а равновесная цена —
.

Пусть правительство
установило налог (per
unit
tax)
в виде фиксированной суммы t
(ден.ед.),
отчисляемой с каждой единицы товара.
Введение потоварного налога приводит
к одинаковому результату независимо
от того, кто непосредственно платит
налог в государственный бюджет —
потребители или производители товара.

Если потоварный
налог уплачивают производители,
то издержки производства каждой единицы
продукции возрастут на величину
потоварного налога. Предложение товара
уменьшится, кривая предложения сдвинется
из положения

в положение

(рис.1). Расстояние по вертикали между
кривыми предложения

равно потоварному налогу t
при любом объеме выпуска.

Рис.1

Потребители покупают
товар по цене

=
(цена
потребителя), из которой производители
уплачивают налог t
за каждую единицу проданного товара.
Фактическая цена, которую получают
производители (фирмы) за каждую единицу
товара, равна Рs
= Рd
– t. По цене Рs
производители поставят на рынок товар
в объеме единиц

.

После применения
налога (независимо от того, на продавца
или потребителя он был наложен) возникает
другая система уравнений:

(2)

Подставим в уравнение
1 системы (2)

,
и приравняем

,
получим:

(3)

Приравняв уравнения
системы, получим: a-b
или

;

Подставив «цену
потребителя» в уравнение 1 системы (2),
определим равновесный объем продаж
после введения налога

,
а вычитая из

налог t, получим «цену производителя»-
Ps.

Упражнение 1.

Предложение
авторучек в селе Замараево задается
функцией
,
а спрос на них

( количество,
штук, P — цена, рублей). Государство вводит
налог, уплачиваемый продавцами, в размере
10 рублей на каждую проданную авторучку.

Определите:

объем продаж и
цену авторучки до и после введения
налога;
чему будут равны
налоговые поступления в бюджет, и как
налоговое бремя распределится между
покупателями и продавцами;
как изменятся
излишки покупателей и продавцов после
введения налога;
чему равна
величина безвозвратных потерь?

Решение:

Определим
первоначальные параметры равновесия.
Приравняем функцию спроса к функции
предложения и определим равновесную
цену, учитывая, что в точке равновесия
Pd=Ps=P.

.

=70;
Q₁=150.
Излишки потребителей
до введения налога: CS_1=

.
Излишки
производителя до введения налога:
PS₁=
Новая (после
введения налога) функция предложения
будет иметь вид:

=3(Р-10)-60=3Р-90.

5. Равновесные
цена и объем продаж после введения
налога составят:

360-3Р = 3P
-90. 450 = 6P.

= 75 (д.е.).Q₂
= 135(шт.).

=P_d—
это «цена потребителя», производитель,
после уплаты налога получит цену

6. Доходы
государственного бюджета от введения
налога составят: Т= Q₂∙t₌1350
д.е.

7. Налоговое бремя
на потребителей Tc=
=(75-70)∙135=5∙135=675.

8. Налоговое бремя
на производителей T_Р=1350-675=675.

9. Излишки
потребителя после введения налога:
CS_2=

.

10. Излишки
производителя после введения налога:
PS_2=

.

11. Чистые потери
общества от введения налога DWL=

Рассмотрим вариант,
соответствующий введению потоварного
налога на потребителей. В этом случае
потребители снизят свой спрос на товар,
и кривая спроса сдвинется вниз вдоль
оси Р на величину налога t. Иными словами,
потребители будут готовы приобрести
такое же, как и прежде, количество товара
только по цене на t ден.ед. ниже
первоначальной.

Подставим в уравнение
1 системы (2)

,
и приравняем

получим

a-b(
)=
.Определим
цену , которую получит производитель
после уплаты налога на производителя:

«Цена потребителя»

.

Подставив «цену
потребителя» в уравнение 1 системы (2)
или «цену производителя» в уравнение
2 системы (2), определим равновесный
объем продаж после введения налога.

Упражнение 2.

Функции спроса
и предложения на рынке товара Х описываются
уравнениями

,

.
Государство вводит фиксированный сбор,
взимаемый с покупателя в 5 ден.ед.

Определите:

объем продаж и
цену товара Х до и после введения налога;
чему будут равны
налоговые поступления в бюджет, и как
налоговое бремя распределится между
покупателями и продавцами;
как изменятся
излишки покупателей и продавцов после
введения налога;
чему равна
величина безвозвратных потерь?

Решение:

Определим
первоначальные параметры равновесия.
Приравняем функцию спроса к функции
предложения и определим равновесную
цену, учитывая, что в точке равновесия
Pd=Ps=P.

=7;
Q₁=23.

Излишки потребителей
до введения налога составляли: CS_1=

.
Излишки
производителя до введения налога
составляли: PS₁=
Новая (после
введения налога) функция спроса будет
иметь вид:

=30-(Рs+5)=25-Ps.

Равновесные цена
и объем продаж после введения налога
составят:

=Ps
= 6 (ден.ед.). Q₂
= 19 ед. Новая равновесная цена

=P_s—
это «цена производителя», потребитель,
после уплаты налога получит цену

Доходы
государственного бюджета от введения
налога составят: Т= Q₂∙t₌19∙5=95
ден.ед.
Налоговое бремя
на потребителей (площадь прямоугольника

)
составит Tc=
=(11-7)∙19=4∙19=76
ден.ед.
Налоговое бремя
на производителей (площадь прямоугольника

)
составит

T_Р=95-76=19
ден.ед.

Излишки потребителей
после введения налога: CS_2=

.
Излишки
производителей после введения налога:
PS_2=

.
Чистые потери
общества от введения налога DWL=

В результате
введения потоварного налога:

сократится
равновесный объем товара, реализуемого
на рынке,
повысится рыночная
цена товара, Р_d
> Р₁;
потребители получат
меньше товара и по более высокой цене;
производители
смогут реализовать меньший объем товара
и по более низкой цене.

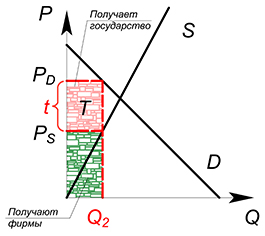
Общая сумма налога
Т, поступающего в бюджет, равна Т=t∙
.
Хотя налог непосредственно платят
продавцы, фактически он распределяется
между покупателями и продавцами:
потребители платят налог

=
,
производители – налог

.
Распределение общей суммы налога Т
между покупателями и продавцами зависит
от эластичности спроса и предложения.

Чем более
эластичен спрос, тем меньшую часть
налога при прочих равных условиях
выплачивают потребители и большую часть
– производители. Чем более эластично
предложение, тем меньшую часть налога
при прочих равных условиях выплачивают
производители и большую часть потребители.

От введения
потоварного налога проиграют и
потребители, и производители. На рынке
данного товара проиграет общество в
целом, так как излишки потребителей и
производителей уменьшатся не только
на величину налоговых поступлений в
бюджет, но и на величину безвозвратных
потерь DWL.
Из производства данного товара ресурсы
перераспределяются в другие отрасли,
что вызовет в них искажения цен и объемов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Рынок товара А представлен следующими функциями спроса и предложения:

Q_D = 400 – 10Р;

Q_S = – 500 + 20Р.

Определите, какую максимальную сумму налога можно собрать с этого рынка путем взимания акциза с каждой проданной единицы товара А?

Решение:

Найдём первоначальное равновесие на рынке. Приравняем функции спроса и предложения:

Q_D = Q_S

400 – 10Р = – 500 + 20Р

30Р = 900

Р_E = 30 — равновесная цена,

Q_E = 400 – 10 × 30 = 100 — равновесный объём.

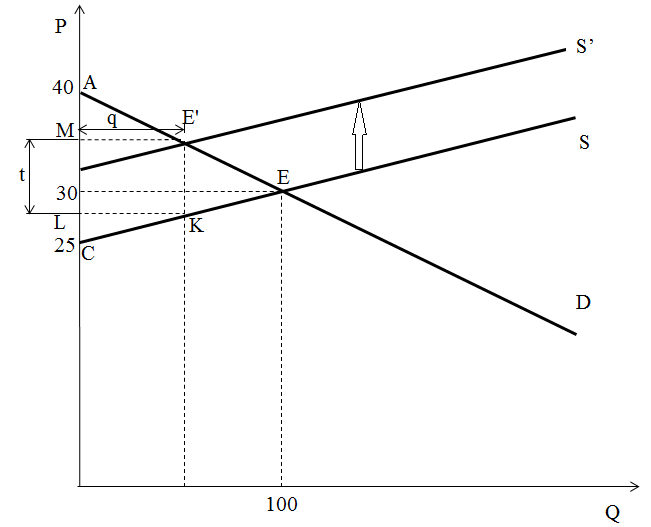
Изобразим ситуацию графически. Найдём координаты точек пересечения графиков функций с осью ординат.

При Q = 0 функция спроса пересекает ось ординат в точке А.

400 – 10Р = 0

Р = 40

При Q = 0 функция предложения пересекает ось ординат в точке С:

– 500 + 20Р = 0

Р = 25

Если государство будет взимать акциз с каждой проданной единицы товара А, то кривая предложения сдвинется вверх на величину акциза в положение S’.

Графически сумма налоговых сборов будет представлена площадью прямоугольника ME’KL, вписанного в треугольник АЕС.

Чтобы найти максимальную сумму налога, необходимо найти функцию площади прямоугольника и решить задачу на максимум функции.

Высота треугольника АЕС равна 100, а основание (40 – 25) = 15

Пусть t, q – длины сторон прямоугольника.

Боковая сторона прямоугольника КЕ’ отсекает ΔКЕ’E, подобный данному ΔAEC.

Высоты в этих треугольниках пропорциональны основаниям, поэтому можно записать:

Отсюда находим t:

Площадь искомого прямоугольника ME’KL:

Найдём максимум этой функции. Для этого определим её производную и приравняем её к нулю.

S’ = 0

15 – 2 × 0,15q = 0

15 = 2 × 0,15q

q = 50

Тогда наибольшее значение функции S при q = 50, равно:

Акциз при этом будет равен:

Итак, максимальная сумма налоговых сборов равна 375, при акцизе 7,5 с каждой проданной единицы товара.

Источник

��

� 2-� ��. �� «�� », ��-��, 2004.

10.8. ��

�� (��. �� 10.�, ��. 10.9), �� , �� , � �� , �� . �� , �� «�� », � �� «�� ». �� .

10.8.1. ��

�� , �� , �� . �� , � �� , �� . 10.17. �� D � MR � �� , �_m � �� , � �� , ��, �� , �� (��, price ceiling � �� ).

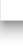
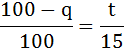
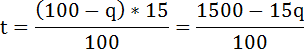
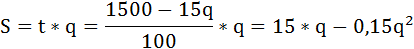
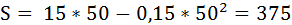
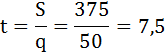
�� , �_m, �� . �� D, �� , �� (�� !) ��. �� , �� ��, �� . �� �_mA � �� BF, �� . �� , �� Q’, �� �_m, �� . �� , �� Q’, �� , �� , � �� , �_m, «�� ».

��  �� �_mA � �� BF. ��, �� (10.2),

MR(Q) = P(Q) + Q(dP/dQ)

�� Q < Q’ � �� �_m, dP/dQ = 0 �, ��, MR(Q) = �_m. �� Q > Q’ �� , �� , �� �_m, �, ��, dP/dQ < 0. ��, �� MR < �. �� , �� Q < Q’ �� �� � �� �_mA, � �� Q > Q’ �� �� ��, �� . ��, �� Q = Q’ �� �� . �� , �� Q = Q’ �� , �� Q’ MR < OR’, � �� MR = O�_m.

�� . �� . 10.18 �� Q* � �� *. ��, �� * �� , �� (Q*, P*). �� . ��, �� P₁, ��  �� P₁AD, � ��  � �� P₁ABF. � �� (SMC) «��» �� , � �� Q₁. �� Q₁. ��, �� , BF, �� , � � �� Q₁.

�� Q₁, �� . � ��, �� P₂ �� Q₂, �� . �� P₂ �� �� �� , �� SMC = AR = �. ��, �� P₃ = minSATC, �� .

10.8.2. ��

�� , �� -��. �� : ��, �� , � �� , ��, �� , � ��, �� (�� ��. pauschal � �� , ��, lump-sum taxes).

�� . �� (�� 2.7) �� . ��

p(Q) = TR(Q) — STC(Q) — �Q.

�� , ��

dp(Q)/dQ = (dTR(Q/i>)/dQ) — (dSTC(Q)/dQ) — T = 0, (10.41)

�. �. ��

MR(Q) = MC(Q) + �.        (10.41*)

�� (�� ), �� . �� (10.41) ��

(d²TR(Q/i>)/dQ²)dQ — (d²STC(Q)/dQ²)dQ — dT = 0,

��

dT/dQ = 1/[d²TR(Q)/dQ² � d²STC(Q)/dQ²].        (10.42)

��, �� (10.12), ��, �� (10.42) �� , dQ/dT < 0 � ��, �� .

�� . 10.19. �� SATC₁ � SMC₁ � �� , Q₁ � P₁ � �� . �� . ��, SMC₂ = SMC₁ + �. �� (10.41*) �� Q₂ � �� P₂. �� (��. 10.19).

�� . � �� . �� , � �� (��, �� ). � ��

p(Q)= TR(Q) — STC(Q) — G,        (10.43)

�� G � �� . ��

dp(Q)/dQ = MR(Q) — SMC(Q) = 0,        (10.44)

��

MR(Q) = SMC(Q).        (10.44*)

�� . 10.20, �� , �� . ��, �� . �� (�� ) �� , �� . �� (10.41*) � (10.44*), ��. 10.19 � 10.20.

�� , �� , �� �� . �� (� ��) t, �� (p_N):

max p_N(Q) =p_N(100 — t) = TR(Q) — STC(Q) — t[TR(Q) — STC(Q)] = (100 — t)[TR(Q) — STC(Q)].      (10.45)

�� , ��, ��

dp_N(Q)/dQ = (100 — t)[MR(Q) � MC(Q)] = 0.        (�.46)

�� t < 100, (100 — t) > 0 �, ��, MR(Q) -MC(Q) = 0 , �. �. MR(Q) = MC(Q) . �� , � �� , � ��, � �� .

—

Источник