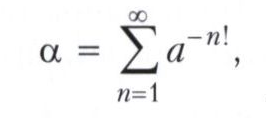Как найти степень алгебраического числа

Содержание.

1. Введение
2. I. Краткий исторический очерк
3. II. Поле алгебраических чисел
4. 2.1. Понятие числового поля
5. 2.2. Алгебраическое число
6. 2.3. Поле алгебраических чисел
7. III. Рациональные приближения алгебраических чисел
8. 3.1 Теорема Лиувиля
9. 3.2 Трансцендентные числа Лиувиля
10. Заключение

Введение.

Первоначальные элементы математики связаны с появлением навыков счета, возникающих в примитивной форме на сравнительно ранних ступенях развития человеческого общества, в процессе трудовой деятельности.

Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел рассматриваются не только натуральные числа, но и множество всех целых чисел, а так же множество рациональных чисел.

Если рассматривать корни многочленов: f(x)=xⁿ+a₁x^n-1+…+a_n с целыми коэффициентами, то обычные целые числа соответствуют случаю, когда этот многочлен имеет степень n=1. Во множестве комплексных чисел естественно выделить так называемые целые алгебраические числа, представляющие собой корни многочленов с целыми коэффициентами.

Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел. Она связана с изучением различных классов алгебраических чисел.

I. Краткий исторический очерк.

Огромное значение в развитии теории чисел имели замечательные работы К. Гаусса (1777-1855). Гаусс наряду с изучением обычных чисел начал рассматривать так же и арифметику чисел, получивших название целых гауссовских чисел, а именно числа вида a+bi, где a и b – обычные целые числа. Эти его исследования положили начала алгебраической теории чисел.

Теория алгебраических чисел была построена в работах Куммера (1810-1893) и Дирихле (1805-1859) и развита затем Кронекером (1823-1891), Дедекиндом (1831-1916) и Е.И. Золотаревым (1847-1878). Работы Лиувилля (1809-1882) и Эрмита (1822-1901) явились основой трансцендентных чисел.

Вопросы аппроксимации алгебраических чисел рациональными были существенно продвинуты в начале века А. Туэ, а затем в пятидесятых годах в работах К. Рота.

В последнее время все большее внимание специалистов по теории чисел привлекает алгебраическая теория чисел.

Здесь надо назвать работы Г. Хассе, Е. Гекке, а в особенности французского математика А. Вейля, результаты которого были использованы во многих теорико-числовых исследованиях, как например Д. Берджессом в проблеме о наименьшем квадратичном вычете.

К алгебраической теории чисел относятся и интересные работы советского математика И.Р. Шафаревича, а так же работы Б.Н. Делонга по теории кубических форм.

II. Поле алгебраических чисел.

2.1 Понятие числового поля

Естественный и важный подход к выделению и изучению тех или иных множеств чисел связан с замкнутостью множеств чисел относительно тех или иных действий.

Определение 1: Мы говорим, что некоторое множество чисел М замкнуто относительно некоторого действия, если для всяких двух чисел их М, для которых определен результат данного действия над ним, число, является этим результатом, всегда принадлежащим М.

Пример:

1. N Множество натуральных чисел замкнуто относительно сложения, т.к. » a, bО N => (a+b) О N.

В отношении умножения множество N так же замкнуто. Но оно не является замкнутым относительно вычитания и деления. Действительно:

5, 7 О N, но 5-7=-2 П N,

3, 2О N, но 3:2=1,5 П N

2. Множество целых чисел Z замкнуто относительно сложения, вычитания и умножения.
3. Множество чисел вида 2^к, кО N, замкнуто относительно умножения и деления.

2к* 2l=2k+l

2к:2l=2k-l

В связи с замкнутостью действий на множестве выделились классы числовых множеств.

Рассмотрим один их классов, называемых полем.

Определение 2: Множество чисел М, содержащие не менее двух чисел, называется числовым полем, если оно замкнуто относительно действий сложения, вычитания, умножения и деления.

Последнее означает, что для любых a, b О M, должно иметь место a+b, a-b, a*b О M. Так же для любого aО M и любого b№ 0 из М, должно выполняться a:bО M.

Пример:

Среди важнейших числовых полей наиболее важными являются:

1. поле всех рациональных чисел;
2. поле всех вещественных чисел;
3. поле всех комплексных чисел.

Что касается множества всех целых чисел, то оно не является числовым полем, ибо не замкнуто относительно деления.

Существует бесконечно много числовых полей. Нас, в данном случае интересует поле алгебраических чисел.

2.2 Определение алгебраического числа.

Существуют различные признаки, по которым их общего множества Z выделяю те или иные подмножества, подвергаемые специальному изучению. С точки зрения важного для алгебры понятия алгебраического уравнения, естественным представляется выделение классов чисел, являющихся корнями алгебраических уравнений, коэффициенты которых принадлежат тому или иному классу чисел.

Определение 3: Число Z называется алгебраическим, если оно является корнем какого-нибудь алгебраического уравнения с целыми коэффициентами:

a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀=0

(a₀, a₁, … ,a_nОZ; a_n№0),

т.е. выполняется:

a_nzⁿ+a_n-1z^n-1+…+a₁z+a₀=0

Числа не являющиеся алгебраическими называются трансцендентными.

В определении алгебраического числа можно допустить, чтобы коэффициенты a₀, a₁, … ,a_n-1, a_n были любыми рациональными числами, поскольку, умножив левую и правую части уравнения на целое число, являющиеся общим кратным знаменателем всех коэффициентов, мы получили уравнение с целыми коэффициентами, корнем которого будет наше число.

К алгебраическим числам принадлежат, в частности, и все рациональные числа. Действительно, рациональное число z= (p, qО N) очевидно является корнем уравнения: qx-p=0.

Также всякое значение корня любой степени из рационального числа является алгебраическим числом. Действительно, число z= (p, qО N) является корнем уравнения:

qxⁿ-p=0.

Существуют и другие алгебраические числа, нежели указанное выше.

Пример:

1. Чиcло z= является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z²=2+2+3. Отсюда z²-5=. Возводя в квадрат обе части этого равенства, получим: z⁴-10z²+25=24. Отсюда следует, что число z является корнем следующего уравнения:

x⁴-10x²+1=0

2. Всякое число z=a+bi, у которого компоненты a и b – рациональные числа, являются алгебраическими. Докажем это.

, (p, q, О N).

Из равенства , получаем: . Отсюда, возводя в квадрат, получим: . Следовательно, z является корнем уравнения:

все коэффициенты которого целые числа.

В дальнейшем мы будем рассматривать только действительные алгебраические числа, не оговаривая этого каждый раз.

Из f(x)=0 следует f(z)j (x)=0, где в качестве j (x) можно взять любой многочлен с целыми коэффициентами. Таким образом для любого алгебраического числа z, из всех этих многочленов обычно рассматривают многочлен наименьшей степени.

Определение 4: Число n называется степенью алгебраического числа z, если z есть корень некоторого многочлена n-ой степени с рациональными коэффициентами и не существует тождественно не равного нулю многочлена с рациональными коэффициентами степени, меньшей чем n, корнем которого является z.

Если корень многочлена n-ой степени с целыми рациональными коэффициентами z не является корнем ни одного тождественно неравного нулю многочлена с целыми коэффициентами степени меньшей чем n, то z не может быть корнем и тождественно неравного нулю многочлена с рациональными коэффициентами степени меньшей чем n, т.е. z – алгебраическое число степени n.

Рациональные числа являются алгебраическими числами первой степени. Любая квадратическая иррациональность представляет собой алгебраическое число 2-й степени, так как, являясь корнем квадратичного уравнения с целыми коэффициентами, она не является корнем какого-либо уравнения 1-й степени с целыми коэффициентами. Алгебраические числа 3-й степени часто называют кубическими иррациональностями, а 4-й степени биквадратическими иррациональностями.

Пример:

1. — алгебраическое число 3-й степени, т.е. кубическая иррациональность. Действительно, это число есть корень многочлена 3-й степени с целыми коэффициентами x³-2=0 и

не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами.

Определение 5: Если алгебраическое число n-й степени z является корнем многочлена f(x)=xⁿ+b₁x^n-1+ … +b_n (nі 1) (1) с рациональными коэффициентами, то f(x) называется минимальным многочленом для z.

Таким образом, минимальным многочленом для z называется многочлен наименьшей степени с рациональными коэффициентами и старшим коэффициентом, равном единице, корнем которого является z.

Если вместо многочлена (1) взять какой-либо другой многочлен с рациональными коэффициентами степени n, корнем которого является z, то многочлен (1) может быть получен из него делением всех коэффициентов на старший член.

Пример:

1. Минимальным многочленом для является x³-2, так как корень этого многочлена

не является корнем какого-либо многочлена степени с рациональными коэффициентами.

Теорема 1: Если f(x) минимальный многочлен алгебраического числа z и f(x) многочлен с рациональными коэффициентами, такой, что F(z)=0, то f(x) делитель F(x), т.е. F(x)=f(x)g(x), где g(x) также многочлен с рациональными коэффициентами.

Доказательство: Согласно известной теореме алгебры F(x) можно представить в виде:

F(x)=f(x)g(x)+r(x)

где g(x) и r(x) – многочлены с рациональными коэффициентами, причем степень r(x) меньше степени f(x). Поскольку F(x)=0 и f(z)=0, то придавая x значение z, получаем r(z)=0; z – корень многочлена r(x) с рациональными коэффициентами степени, меньшей чем у минимального для z многочлена, т.е. меньшей чем степень z. Это может быть только если r(x) тождественно равен нулю, а значит F(x)=f(x)g(x). Теорема доказана.

Теорема 2: Для любого алгебраического числа z минимальный многочлен неприводим над полем рациональных чисел.

Доказательство:

Пусть f(x) – минимальный многочлен для z. Предположим, что f(x) приводим над полем рациональных чисел, т.е., что f(x)=w (x)j (x), w (x)j (x) – многочлены с рациональными коэффициентами, степени меньшей, чем n.

Из равенства w (x)j (x)=f(x)=0 следует, что из двух чисел w (x) и j (x), по крайней мере одно равно нулю. Пусть например w (x)=0, тогда z – корень тождественно не равного нулю многочлена w (x) с рациональными коэффициентами, степени меньшей, чем n, т.е. меньшей чем у f(x). А это противоречит тому, что f(x) – минимальный многочлен для z. Предположение, что f(x) приводим над полем рациональных чисел, оказалось неверным, т.е. f(x) неприводим над этим полем. Теорема доказана.

Теорема 3: Если z корень неприводимого над полем рациональных чисел многочлена F(x) с рациональными коэффициентами степени n, то z – алгебраическое число степени n.

Доказательство:

Обозначим минимальный многочлен для z через f(x). Согласно теоремы 1: F(x)=f(x)g(x); где g(x) – многочлен с рациональными коэффициентами. Поскольку F(x) неприводим над полем рациональных чисел и f(x) отлично от постоянного, то g(x)=c, где c – рационально. F(x)=cf(x), т.е. z – алгебраическое число n-й степени. Теорема доказана.

Пример:

Пусть p – простое число.

при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена.

x^p-a=0

Если z – алгебраическое число степени n и f(x) – минимальный многочлен для z, то все корни z₁, z₂, … z_n уравнения f(x)=0, отличные от z, называют сопряженным с z.

Один из корней совпадает с z, будем ставить его на первое место, т.е. z=z₁.

2.3. Поле алгебраических чисел

Теорема 4: Множество всех действительных алгебраических чисел представляет собой поле, т.е. сумма, разность, произведение и частное двух алгебраических чисел a и b (для частного при b№ 0) являются алгебраическими числами.

Доказательство:

1. Пусть a — корень многочлена f(x) степени n с целыми коэффициентами, корни которого a₁, a₂, … ,a_n, a и b — корень многочлена j (x) степени m с целыми коэффициентами, корни которого b₁, b₂, … b_m (b =b₁). Рассмотрим многочлен:

F(x)=(x-(a_i+b_i))=

= (x-a₁-b₁) (x-a₁-b₂) … (x-a₁-b_m)

(x-a₂-b₁) (x-a₂-b₂) … (x-a₂-b_m)

— — — — — — — — — — — — — — — — — — — — — — — — — —

(x-a_n-b₁) (x-a_n-b₂) … (x-a_n-b_m) (2)

Если в этом произведении сделать какую угодно подстановку величин a₁, a₂, … ,a_n, то некоторые строки переставляется местами, но произведение в целом не изменится. Это значит, что F(x) – симметрический многочлен по отношению b₁, b₂, … b_m. В целом F(x) – симметрический многочлен от двух систем аргументов: a₁, a₂, … ,a_n и b₁, b₂, … b_m.

Согласно известным теоремам о симметрических многочленах, коэффициенты многочлена F(x) могут быть выражены рационально через элементарные симметрические функции от a₁, a₂, … ,a_n и b₁, b₂, … b_m, т.е. через целые коэффициенты, f(x) и j (x). Это значит, что коэффициенты F(x) рациональны, и, следовательно, число a +b =a₁+b₁, являющегося, как это непосредственно видно из формулы (2), корнем F(x), есть алгебраическое число.

2. Для доказательства того, что произведение двух алгебраических чисел a и b есть алгебраическое число, достаточно, аналогично тому, как это было только что сделано для многочлена (2), рассмотреть многочлен:

F(x)=(x-a_{ib i}) (3)

Этот многочлен имеет в качестве одного из своих корней a_{1b 1}=ab .

3. Пусть b — корень многочлена j (x)=b₀xⁿ+ b₁x^n-1+ … b_n, (b_i – целые числа). Тогда -b является корнем многочлена с целыми коэффициентами.

j (-x)=(-1)ⁿb₀xⁿ+(-1)^n-1b₁x^n-1+ … bⁿ, а при b№ 0 корень многочлена x^nj()=b₀+b₁x+ … b_nxⁿ. Таким образом, вместе с b алгебраическими числами являются -b и .

Разность может быть представлена в виде a +(-b ), т.е. в виде суммы двух алгебраических чисел. При b№ 0 частное , являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число.

Если степени алгебраических чисел a и b равны m и n, то, взяв в качестве f(x) и j (x) соответствующие минимальные многочлены будем в (2) и (3) иметь многочлены степени mn, и ab алгебраические числа степени, не большей, чем mn. Многочлены j (x), j (-x), и xⁿ одинаковой степени, а, следовательно, b , -b , — алгебраические числа одной и той же степени, откуда следует, что и a -b и имеют степени не больше, чем mn. Теорема доказана.

Пример:

1) и алгебраические числа 2-й степени, а — алгебраическое число 4 степени. Действительно, если a =, то a²=5+, 2⁴-10a²+1=0, т.е. a корень многочлена f(x)=x4-10×2+1 с целыми коэффициентами, и f(x)=(x-)(x-)(x+)(x+) (4)

Из теоремы единственности над полем рациональных чисел множители f(x) должны являться произведением каких-то множителей правой части равенства (4). Легко видеть, что из этих множителей нельзя составить многочлен с рациональными коэффициентами степени меньшей, чем 4, т.е. f(x) – неприводимый над полем рациональных чисел многочлен, а, следовательно, согласно теореме 3, — алгебраическое число 4-й степени.

2) a = и b =, как легко видеть, это алгебраические числа 6-й степени, а произведение ab = — алгебраическое число 3-й степени.

III. Рациональные приближения

алгебраических чисел.

3.1. Теорема Лиувилля.

Алгебраические числа не могут иметь слишком хороших рациональных приближений: погрешность при замене алгебраического числа рациональной дробью не может быть достаточно мала по порядку в сравнении с величиной, обратной знаменателю рациональной дроби.

Для алгебраического числа 1-й степени существует постоянная c>0, такая, что для любой рациональной дроби , отличной от a , будет выполняться неравенство:

(5)

Для алгебраического числа 2-й степени можно подобрать c>0, такое, что для любой рациональной дроби, будет иметь место неравенство:

(6)

В 1844 г., французским математиком Лиувиллем, впервые была доказана общая теорема:

Теорема 5: Для любого действительного алгебраического числа a степени n можно подобрать положительноеc, зависящее только от a , такое, что для всех рациональных чисел (№a ) будет иметь место неравенство:

(7)

Доказательство:

Пусть f(x)=A₀xⁿ+ A₁x^n-1+A_n неприводимый многочлен с целыми коэффициентами, корнем которого является a . В качестве f(x) можно, например, взять многочлен, получающийся из минимального для a многочлена после умножения всех коэффициентов на наименьшее кратное их знаменателей.

Согласно теореме Безу, имеем:

f(x)=(x-a )g(x), (8)

где g(x) – многочлен с действительными коэффициентами.

Возьмем произвольное d >0. |g(x)| — непрерывная, а следовательно, ограниченная функция от x в сегменте [a -d ; a +d] , т.е. существует положительное число M, такое, что |g(x)|Ј M, для всех x из этого сегмента. Обозначим через c=min , так, что и .

Для произвольного рационального числа могут представиться две возможности:

1. лежит вне сегмента |a -dm ; a +dm |, тогда
2. 

удовлетворяет неравенствам:

a -dЈЈa +d , тогда |g()|Ј M и, подставляя в (8) вместо x значение , получаем:

(9)

Неприводимый над полем рациональных чисел многочлен f(x) степени nі 2 не имеет рациональных корней, а при n=1 не имеет корней, отличных от a , так что:

f()=

Поскольку числитель — целое неотрицательное, отличное от нуля, т.е. число большее или равное 1, то (10). Сравнивая неравенства (9) и (10) получаем , так что и в этом случае имеем: . Теорема доказана.

Пример:

Пусть z – неквадратное целое число. Найти c>0, такое, что для всех рациональных чисел имело бы место неравенство:

.

— корень многочлена xa -В. Деля x²-D на x-, находим g(x)=x+.

При -d<x<+dимеем , т.е. M=+d . В качестве c берем , при этом выгодней всего взять d так, что d²+d-1=0, т.е. d=.

При таком d получаем , так что при любых целых a и b имеем: .

3.2. Трансцендентные числа Лиувилля.

Числа, являющиеся корнями уравнений с целыми коэффициентами, не исчерпывают все множество действительных чисел, т.е. существуют действительные числа отличные от алгебраических.

Определение 6: Любое неалгебраическое число называется трансцендентным.

Впервые существование трансцендентных чисел доказано Лиувиллем. Доказательство существования трансцендентных чисел у Лаувилля эффективно; на основе следующей теоремы, являющейся непосредственным следствием теоремы 5, строятся конкретные примеры трансцендентных чисел.

Теорема 6: Пусть a – действительное число. Если для любого натурального nі1 и любого действительного c>0 существует хотя бы одна рациональная дробь , такая, что (11), то a – трансцендентное число.

Доказательство:

Если бы a было алгебраическим, то нашлось бы (теорема 5) целое положительное n и действительное c>0 такие, что для любой дроби было бы , а это противоречит тому, что имеет место (11). Предположение, что a алгебраическое число, т.е. трансцендентное число. Теорема доказана.

Числа a , для которых при любых nі1 и c>0 неравенство (11) имеет решение в целых числах a и b называются трансцендентными числами Лиувилля.

Пример:

1. 

a – трансцендентное число.

Возьмем произвольные действительные nі1 и c>0. Пусть , где k выбрано настолько большим, что и kі n, тогда

Поскольку для произвольных nі1 и c>0 можно найти дробь такую, что , то a – трансцендентное число.

Заключение.

Алгебраические числа имеют широкое применение в теории чисел, алгебре, геометрии и других разделов математики. Они позволяют раскрыть вариантности алгебры для практических приложений. Это имеет большое значение в подготовке учителя для средней школы.

Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел.

К этому разделу относятся вопросы, связанные с изучением различных классов алгебраических чисел.

Эта работа может служить в качестве учебного пособия при изучении теории алгебраических чисел. А так же она удобна в использовании при подготовке к экзамену.

В работе введена сплошная нумерация теорем и определений арабскими цифрами. Все теоремы даны с полными доказательствами. Приведенные примеры алгебраических чисел и действий над ними, даны с доступными пояснениями и, при необходимости, с доказательством.

Большое место в работе занимают теоретические сведения о развитии алгебры теории чисел. Помимо введения, дающего общий очерк развития теории чисел, первый параграф посвящен уже конкретно развитию теории алгебраических чисел. Так же на протяжении всей работы можно наблюдать исторические комментарии.

Данная работа дает представление о современном состоянии рассматриваемого вопроса и дает представление о теории алгебраических чисел и о теории чисел вообще, как о развивающейся науке.

Алгебраи́ческое число́ над полем — элемент алгебраического замыкания поля , то есть корень многочлена с коэффициентами из .

Если поле не указывается, то предполагается поле рациональных чисел, то есть , в этом случае поле алгебраических чисел обычно обозначается .
Поле является подполем поля комплексных чисел.

Эта статья посвящена именно этим «рациональным алгебраическим числам».

Связанные определения

Примеры

Свойства

История

Впервые алгебраические поля стал рассматривать Гаусс.
При обосновании теории биквадратичных вычетов он развил арифметику целых гауссовых чисел, то есть чисел вида , где и — целые числа.
Далее, изучая теорию кубических вычетов, Якоби и
Эйзенштейн (F. Eisenstein) создали арифметику чисел
вида , где — кубический корень из единицы, а и — целые числа.
В 1844 году Ж. Лиувилль доказал теорему о невозможности слишком хорошего приближения корней многочленов с рациональными коэффициентами рациональными дробями, и, как следствие, ввёл формальные понятия алгебраических и трансцендентных (т. е. всех прочих вещественных) чисел.
Попытки доказать великую теорему Ферма привели Э. Куммера (Е. Kummer) к изучению полей деления круга, введению понятия идеала и созданию элементов теории алгебраических чисел.
В работах Дирихле,
Кронекера,
Гильберта
и других теория алгебраических чисел получила свое дальнейшее развитие.
Большой вклад в неё внесли русские математики
Е. И. Золотарев (теория идеалов),
Г. Ф. Вороной (кубические иррациональности, единицы кубических полей),
А. А. Марков (кубическое поле),
Ю. В. Сохоцкий (теория идеалов)
и другие.

Ссылки

• Фельдман, Н. Алгебраические и трансцендентные числа // Квант, № 7, 1983.

п·о·р Числа
Счётные множества
Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые • Арифметические
Вещественные числа и их расширения
Вещественные () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Дуальные • Гиперкомплексные • Супердействительные • Гиперреальные • Шаблон:Нп5
Инструменты расширения числовых систем
Процедура Кэли — Диксона • Теорема Фробениуса • Теорема Гурвица
Иерархия чисел
Шаблон:Иерархия чисел
Другие числовые системы
Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также
Двойные числа • Иррациональные числа • Трансцендентные числа • Числовой луч • Бикватернион
Степени тысячи
Тысяча*Миллион*Миллиард*Биллион*Триллион*Квадриллион*…*Центиллион
Древнерусские числа
Мириада*Лакх*Крор*Гугол*Асанкхейя*Гуголплекс
Прочие степени десяти
Мириада*Лакх*Крор*Гугол*Асанкхейя*Гуголплекс
Степени двенадцати
Дюжина*Гросс*Масса
Прочие целые
0*1*Чёртова дюжина*Число зверя*Число Рамануджана — Харди*Число Грэма*Число Скьюза*Число Мозера
Прочие числа
Пи*e (число Эйлера)*φ (Золотое сечение)*Серебряное сечение*Постоянная Эйлера — Маскерони*Постоянные Фейгенбаума*Постоянная Гельфонда*Константа Бруна*Постоянная Каталана*Постоянная Апери*Мнимая единица

Шаблон:Категория только в статьях

ar:عدد جبري
bg:Алгебрично число
bn:বীজগাণিতিক সংখ্যা
cs:Algebraické číslo
da:Algebraiske tal
el:Αλγεβρικός αριθμός
fa:عدد جبری
gl:Número alxébrico
he:מספר אלגברי
hu:Algebrai szám
nl:Algebraïsch getal
nn:Algebraiske tal
pl:Liczby algebraiczne
sk:Algebrické číslo
sr:Алгебарски број
sv:Algebraiskt tal
ta:இயற்கணித எண்களும் விஞ்சிய எண்களும்
vi:Số đại số

From Wikipedia, the free encyclopedia

An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x² − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x⁴ + 4.

All integers and rational numbers are algebraic, as are all roots of integers. Real and complex numbers that are not algebraic, such as π and e, are called transcendental numbers.

The set of algebraic numbers is countably infinite and has measure zero in the Lebesgue measure as a subset of the uncountable complex numbers. In that sense, almost all complex numbers are transcendental.

Examples[edit]

• All rational numbers are algebraic. Any rational number, expressed as the quotient of an integer a and a (non-zero) natural number b, satisfies the above definition, because x = a/b is the root of a non-zero polynomial, namely bx − a.^[1]
• Quadratic irrational numbers, irrational solutions of a quadratic polynomial ax² + bx + c with integer coefficients a, b, and c, are algebraic numbers. If the quadratic polynomial is monic (a = 1), the roots are further qualified as quadratic integers.
  • Gaussian integers, complex numbers a + bi for which both a and b are integers, are also quadratic integers. This is because a + bi and a — bi are the two roots of the quadratic x² — 2ax + a² + b².
• A constructible number can be constructed from a given unit length using a straightedge and compass. It includes all quadratic irrational roots, all rational numbers, and all numbers that can be formed from these using the basic arithmetic operations and the extraction of square roots. (By designating cardinal directions for 1, −1, i, and −i, complex numbers such as are considered constructible.)
• Any expression formed from algebraic numbers using any combination of the basic arithmetic operations and extraction of nth roots gives another algebraic number.
• Polynomial roots that cannot be expressed in terms of the basic arithmetic operations and extraction of nth roots (such as the roots of x⁵ − x + 1). That happens with many but not all polynomials of degree 5 or higher.
• Values of trigonometric functions of rational multiples of π (except when undefined): for example, cos π/7, cos 3π/7, and cos 5π/7 satisfy 8x³ − 4x² − 4x + 1 = 0. This polynomial is irreducible over the rationals and so the three cosines are conjugate algebraic numbers. Likewise, tan 3π/16, tan 7π/16, tan 11π/16, and tan 15π/16 satisfy the irreducible polynomial x⁴ − 4x³ − 6x² + 4x + 1 = 0, and so are conjugate algebraic integers.
• Some but not all irrational numbers are algebraic:

Properties[edit]

• If a polynomial with rational coefficients is multiplied through by the least common denominator, the resulting polynomial with integer coefficients has the same roots. This shows that an algebraic number can be equivalently defined as a root of a polynomial with either integer or rational coefficients.
• Given an algebraic number, there is a unique monic polynomial with rational coefficients of least degree that has the number as a root. This polynomial is called its minimal polynomial. If its minimal polynomial has degree n, then the algebraic number is said to be of degree n. For example, all rational numbers have degree 1, and an algebraic number of degree 2 is a quadratic irrational.
• The algebraic numbers are dense in the reals. This follows from the fact they contain the rational numbers, which are dense in the reals themselves.
• The set of algebraic numbers is countable (enumerable),^[3][4] and therefore its Lebesgue measure as a subset of the complex numbers is 0 (essentially, the algebraic numbers take up no space in the complex numbers). That is to say, «almost all» real and complex numbers are transcendental.
• All algebraic numbers are computable and therefore definable and arithmetical.
• For real numbers a and b, the complex number a + bi is algebraic if and only if both a and b are algebraic.^[5]

Field[edit]

The sum, difference, product and quotient (if the denominator is nonzero) of two algebraic numbers is again algebraic, as can be demonstrated by using the resultant, and algebraic numbers thus form a field (sometimes denoted by , but that usually denotes the adele ring). Every root of a polynomial equation whose coefficients are algebraic numbers is again algebraic. That can be rephrased by saying that the field of algebraic numbers is algebraically closed. In fact, it is the smallest algebraically-closed field containing the rationals and so it is called the algebraic closure of the rationals.

The set of real algebraic numbers itself forms a field.^[6]

[edit]

Numbers defined by radicals[edit]

Any number that can be obtained from the integers using a finite number of additions, subtractions, multiplications, divisions, and taking (possibly complex) nth roots where n is a positive integer are algebraic. The converse, however, is not true: there are algebraic numbers that cannot be obtained in this manner. These numbers are roots of polynomials of degree 5 or higher, a result of Galois theory (see Quintic equations and the Abel–Ruffini theorem). For example, the equation:

has a unique real root that cannot be expressed in terms of only radicals and arithmetic operations.

Closed-form number[edit]

Algebraic numbers are all numbers that can be defined explicitly or implicitly in terms of polynomials, starting from the rational numbers. One may generalize this to «closed-form numbers», which may be defined in various ways. Most broadly, all numbers that can be defined explicitly or implicitly in terms of polynomials, exponentials, and logarithms are called «elementary numbers», and these include the algebraic numbers, plus some transcendental numbers. Most narrowly, one may consider numbers explicitly defined in terms of polynomials, exponentials, and logarithms – this does not include all algebraic numbers, but does include some simple transcendental numbers such as e or ln 2.

Algebraic integers[edit]

An algebraic integer is an algebraic number that is a root of a polynomial with integer coefficients with leading coefficient 1 (a monic polynomial). Examples of algebraic integers are and Therefore, the algebraic integers constitute a proper superset of the integers, as the latter are the roots of monic polynomials x − k for all . In this sense, algebraic integers are to algebraic numbers what integers are to rational numbers.

The sum, difference and product of algebraic integers are again algebraic integers, which means that the algebraic integers form a ring. The name algebraic integer comes from the fact that the only rational numbers that are algebraic integers are the integers, and because the algebraic integers in any number field are in many ways analogous to the integers. If K is a number field, its ring of integers is the subring of algebraic integers in K, and is frequently denoted as O_K. These are the prototypical examples of Dedekind domains.

Special classes[edit]

• Algebraic solution
• Gaussian integer
• Eisenstein integer
• Quadratic irrational number
• Fundamental unit
• Root of unity
• Gaussian period
• Pisot–Vijayaraghavan number
• Salem number

Notes[edit]

References[edit]

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 0-13-004763-5, MR 1129886
• Hardy, G. H. and Wright, E. M. 1978, 2000 (with general index) An Introduction to the Theory of Numbers: 5th Edition, Clarendon Press, Oxford UK, ISBN 0-19-853171-0
• Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory, Graduate Texts in Mathematics, vol. 84 (Second ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4757-2103-4, ISBN 0-387-97329-X, MR 1070716
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
• Niven, Ivan 1956. Irrational Numbers, Carus Mathematical Monograph no. 11, Mathematical Association of America.
• Ore, Øystein 1948, 1988, Number Theory and Its History, Dover Publications, Inc. New York, ISBN 0-486-65620-9 (pbk.)

АЛГЕБРАИЧЕСКОЕ ЧИСЛО, число а, удовлетворяющее уравнению f(х) = 0, где

n, a_n, a_n-1,.. a₁, a₀ — целые числа, n≥1, аn ≠ 0, наибольший общий делитель чисел a_n,a_n-1,…,а₁,а₀ равен единице; другими словами, f(α) = 0, т. е. а является корнем многочлена f(х). Примеры алгебраических чисел:

Любое рациональное число α = b/а, где а и b — целые числа, а≠0, является алгебраическим, так как оно — корень многочлена f(х) = ax-b. Степенью алгебраического числа α называется наименьшая из степеней всех не равных тождественно нулю многочленов с целыми коэффициентами, имеющих α своим корнем. В приведённых примерах число α₁ имеет степень 3, а числа α₂ и α₃ — степень 2. Рациональные числа и только они имеют степень 1. Действительное или комплексное число α называется трансцендентным, если оно не является алгебраическим. Т. о., трансцендентное число не может быть корнем никакого многочлена f(х) с целыми коэффициентами, f(х) ≠0. Т.к. множество всех многочленов с целыми коэффициентами счётно, то и множество алгебраических числе счётно. Множество всех действительных чисел несчётно (теорема Кантора), т. е. почти все действительные числа трансцендентны. Однако доказательство трансцендентности конкретного числа часто оказывается трудной задачей, и для доказательства трансцендентности разработаны специальные аналитические методы.

Алгебраические числа плохо приближаются рациональными числами; например, справедлива следующая теорема Лиувилля: если α действительное алгебраическое число степени n, n≥2, то существует положительное число С, зависящее только от α, такое, что при любых целых числах р и q, q> 0, выполняется неравенство:

Из этой теоремы, в частности, следует, что числа α вида

где целое число а ≥ 2 (числа Лиувилля), являются трансцендентными.

Если α – алгебраическое число степени n и, кроме того, многочлен f(х) степени n, корнем которого является α, имеет старший коэффициент a_n = 1, то α называется целым алгебраическим числом. Построена арифметика алгебраических чисел, похожая на обычную арифметику целых чисел, но имеются и принципиальные отличия от последней. В частности, в некоторых случаях в такой арифметике не выполняется теорема об однозначном разложении целых чисел на простые сомножители. Алгебраические числа находят применения в теории диофантовых уравнений.

Лит.: Гекке Э. Лекции по теории алгебраических чисел. М.; Л., 1940; Боревич З.И., Шафаревич И. Р. Теория чисел. 3-е изд. М., 1985; Галочкин А. И., Нестеренко Ю.В., Шидловский А. Б. Введение в теорию чисел. 2-е изд. М., 1995.   

А. А. Карацуба.

sub

Возведение числа в степень является важнейшей математической операцией, часто используемой для различных вычислений. В зависимости от вида основания и показателя значение степени рассчитывается по-разному. Ниже будут подробно рассмотрены основные правила нахождения значений степеней.

Возведение числа в степень с натуральным показателем

Прежде чем приступить к изучению операции возведения в степень необходимо рассмотреть базовое понятие натуральной степени числа.

Таким образом, для натурального показателя степень представляет собой укороченную запись умножения одинаковых множителей. В данном случае чтобы найти значение степени, следует перемножить число, которое является основанием, само на себя указанное количество раз.

Пример 1

Рассмотрим возведение числа 3 в степень 5. Согласно приведенному выше базовому определению:

3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Для операций возведения во вторую и третью степень имеются устоявшиеся названия: возведение в квадрат и куб, соответственно. Таким образом, выражение «3²» может быть прочитано как «три во второй степени» или «три в квадрате», оба варианта будут верными.

Значение степенных выражений с дробным основанием и натуральным показателем находится по той же схеме. В то же время, в соответствии с правилом умножения дробей, операция возведения дроби в степень может быть разбита на два действия, когда числитель и знаменатель возводятся в соответствующую показателю степень по отдельности.

Пример 2

Найдем, чему будут равны [ frac{2}{5} ] в степени 3:

[left(frac{2}{5}right)^{3}=frac{2}{5} times frac{2}{5} times frac{2}{5}=frac{2^{3}}{5^{3}}=frac{8}{125}]

Операция возведения в натуральную степень имеет определенные особенности при работе с отрицательными числами. Рассмотрим следующий пример:

Пример 3

Найдем значения степенных выражений (-5)³ и (-5)⁴. Для этого, согласно базовому определению, необходимо умножить основание само на себя 3 и 4 раза соответственно:

(-5)³ = (-5) × (-5) × (-5) = -125

(-5)⁴ =(-5) × (-5) × (-5) × (-5) = 625

Из приведенного примера можно видеть, что в первом случае полученный результат является отрицательным числом, а во втором – положительным. Это связано с правилом перемножения отрицательных чисел. Следствием из него является то, что если показатель степени отрицательного числа представляет собой четное число, результат будет положительным, если нечетное – отрицательным. Таким образом, степень с отрицательным основанием и четным показателем будет равна степени с таким же показателем и основанием, равным по модулю, но противоположным по знаку.

(-a)²ⁿ = a²ⁿ

Если требуется возвести в натуральную степень иррациональное число, то его необходимо предварительно округлить до той значащей цифры, которая позволит получить ответ с требуемой точностью. Рассмотрим данный случай на примере числа π.

Пример 4

Выполним возведение в степень 3 числа π.

π – это бесконечное иррациональное число. С точностью до 10 знаков после запятой оно записывается следующим образом:

π = 3,1415926536

Допустим, нам необходим результат с точностью два знака после запятой. Тогда число π может быть округлено до 3,14.

(3,14)³ = 3,14 × 3,14 × 3,14 ≈ 30,96

Отдельно следует отметить, чему будет равно число в степени 1. В соответствии с базовым определением

[a^{n}=underbrace{a times a times ldots times a}_{text {п множсителей }}]

вне зависимости от значения основания, число в степени 1 равно самому себе.

На практике возможны и более сложные случаи, когда требуется найти значение степенного выражения, в котором показатель не является натуральным числом. Ниже будут рассмотрены ситуации, когда показатель степени представляет собой целое, дробное, рациональное или иррациональное число.

Вычисление степеней с целым показателем

Все операции по возведению в целую степень можно разделить на три группы: когда показатель является целым положительным (натуральным) числом, когда он равен нулю, и когда он является отрицательным числом.

Случай с натуральным показателем был рассмотрен ранее, поэтому мы не будем к нему возвращаться.

В случае, когда показатель равен нулю, для любого не равного нулю основания значение степени будет равно единице. Если же и основание, и показатель степени равны нулю значение выражения будет не определено.

Пример 5

Рассмотрим возведение в нулевую степень натурального, дробного, иррационального чисел, а также нуля:

10⁰ = 1

0,5⁰ = 1

π⁰ = 1

0⁰ – не определено.

Осталось рассмотреть нахождение значения степенного выражения с целым отрицательным показателем. Число а в степени -n представляет собой дробь, числитель которой равен единице, а знаменатель – числу а в степени n.

[a^{-n}=frac{1}{a^{n}}]

Можно видеть, что знаменатель дроби является натуральной степенью, вычисление которой было рассмотрено ранее. Таким образом, две степени, у которых основания одинаковы, а показатели противоположны по знаку, но равны по модулю, будут являться обратными числами. Рассмотрим возведение в отрицательную степень целого и дробного чисел:

Пример 6

Вычислим, чему равно 7 в степень -3:

[7^{-3}=frac{1}{7^{3}}=frac{1}{7 times 7 times 7}=frac{1}{343}]

Пример 7

Найдем значение степенного выражения [left(frac{2}{9}right)^{-2}]

При возведении дробного числа в отрицательную степень на определенном этапе осуществляется «переворот» дроби. Он может быть выполнен как в конце вычислений:

[left(frac{2}{9}right)^{-2}=frac{1}{left(frac{2}{9}right)^{2}}=frac{1}{frac{2}{9} times frac{2}{9}}=frac{1}{frac{4}{81}}=frac{81}{4}=20 frac{1}{4}]

так и в начале:

[left(frac{2}{9}right)^{-2}=left(frac{9}{2}right)^{2}=frac{81}{4}=20 frac{1}{4}]

Из-за указанного в примере «переворота», при возведении десятичной дроби в отрицательную степень рекомендуется предварительно преобразовать основание к форме обыкновенной дроби. Рассмотрим данную ситуацию на примере:

Пример 8

Найдем значение степенного выражения 0,5^-2:

[0,5^{-2}=left(frac{5}{10}right)^{-2}=left(frac{10}{5}right)^{2}=frac{10^{2}}{5^{2}}=frac{100}{25}=4]

Отдельно следует упомянуть о выражениях с целым отрицательным показателем, основание которых равно нулю. Подобное выражение будет не определено, поскольку его преобразование будет приводить к дроби, знаменатель которой равен нулю.

[0^{-n}=frac{1}{0^{n}}] ‒ выражение не определено.

Возведение числа в дробную степень

Прежде чем приступить к вычислению, следует рассмотреть базовое определение степени с дробным показателем. В виде формулы оно может быть записано следующим образом:

[a^{m / n}=sqrt[n]{a^{m}}, text { где }]

a – положительное число;

m – целое число;

n – натуральное число.

Из указанного определения следует, что операция нахождения алгебраического корня любой степени также может быть представлена в форме возведения в дробную степень, когда числитель показателя равен единице, а знаменатель – основанию корня.

[sqrt[n]{a}=a^{1 / n}]

При этом не следует воспринимать данное свойство как способ преобразования иррационального числа в рациональное. Изменяется только форма записи. Например, если число √2 является иррациональным, то при записи его в форме [2^{1 / 2}] оно также останется иррациональным.

При нахождении значения степени с дробным показателем следует последовательно выполнить два математических действия: возведение основания в степень с целым показателем m и извлечение корня n-ной степени. При этом согласно свойству корней, указанные действия можно выполнить и в обратной последовательности, то есть можно сначала извлечь из основания корень n-й степени, а затем возвести полученный результат в степень m.

[sqrt[n]{a^{m}}=(sqrt[n]{a})^{m}]

Рассмотрим оба способа вычисления степеней с дробным показателем на конкретном примере.

Пример 9

Найдем значение степенного выражения [128^{5 / 7}].

Способ 1. Возведение в степень подкоренного выражения с последующим извлечением корня

[128^{5 / 7}=sqrt[7]{128^{5}}=sqrt[7]{34359738368}=32]

В данном случае из-за большого значения числа под корнем найти значение выражения, не прибегая к помощи калькулятора, невозможно.

Способ 2. Извлечение корня из основания с последующим возведением в степень.

[128^{5 / 7}=(sqrt[7]{128})^{5}=2^{5}=32]

Указанный способ нахождения значения степени существенно легче. При этом результат вычислений не отличается, то есть можно выбирать тот способ, который будет удобнее в конкретном случае.

Если показатель степени представлен в форме десятичной дроби, то удобнее будет записать его в виде обычной.

Пример 10

Вычислим значение степени [243^{0,4}]:

[243^{0,4}=243^{4 / 10}=243^{2 / 5}=(sqrt[5]{243})^{2}=3^{2}=9]

В случае, когда показатель представляет собой смешанное число, для удобства вычислений он может быть записан в виде неправильной дроби.

Пример 11

Вычислим значение выражения:

[left(12 frac{1}{4}right)^{1 frac{1}{2}}=left(frac{49}{4}right)^{3 / 2}=left(sqrt{frac{49}{4}}right)^{3}=left(frac{7}{2}right)^{3}=frac{343}{8}=42 frac{7}{8}]

Следует обратить внимание на математическую операцию возведения в отрицательную дробную степень. В этом случае вычисления производятся в три этапа: нахождение числа, обратного исходному, извлечение корня, степень которого соответствует значению знаменателя показателя, и возведение в степень, соответствующую числителю дробного показателя. Как и в случае с положительным дробным показателем, указанные действия могут выполняться в любой последовательности.

Пример 12

Найдем значение выражения [49^{-1 / 2}].

Выполним преобразование числа в обратное ему:

[49^{-1 / 2}=frac{1}{49^{1 / 2}}]

Найдем значение степени в знаменателе полученной дроби:

[frac{1}{49^{1 / 2}}=frac{1}{sqrt{49}}=frac{1}{7}]

Также необходимо рассмотреть случай, когда основанием степени является ноль, а показателем – дробное число. Как и в случае с целыми показателями, подобные выражения имеют смысл лишь в том случае, когда показатель больше нуля. В противном случае выражение будет не определено.

Нахождение степеней с иррациональным показателем

Иногда возникает необходимость нахождения значения степени, показатель которой представляет собой иррациональное число. Проблема заключается в том, что найти точное значение подобного выражения невозможно. Однако для решения любой практической задачи, как правило, достаточно нахождения значения степенного выражения с определенной степенью точности. В этом случае иррациональный показатель округляется до требуемого десятичного знака, после чего вычисление осуществляется согласно правилам, принятым для дробного показателя.

Рассмотрим решение подобной задачи на конкретном примере:

Пример 13

Предположим, что нам необходимо найти значение выражения 2 в степени √2. Показатель степени является иррациональным числом. В виде бесконечной десятичной дроби оно может быть записано следующим образом:

√2 = 1,41421356…

Найдем значение выражения с различной степенью приближения.

Вариант 1.

Округлим значение иррационального числа до двух цифр после запятой и найдем приближенное значение степени:

[√2≈1,41]

[2^{sqrt{2}} approx 2^{1,41} approx 2,65737]

Вариант 2.

Округлим значение иррационального числа до четырех цифр после запятой и найдем приближенное значение степени:

[√2≈1,4142]

[2^{sqrt{2}} approx 2^{1,4142} approx 2,66512]

Можно видеть, что полученные значения различаются во втором знаке после запятой, при этом второе значение является более точным.

В большинстве случаев вычисление степеней с иррациональными показателями является сложной задачей, для решения которой используется вычислительная техника.