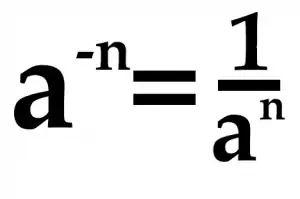Как найти степень числа если калькулятор - Исправление недочетов и поиск решений вместе с Examum.ru

Как посчитать степень

Главная
/
Математика
/
Арифметика
/
Как посчитать степень

Для того чтобы возвести любое число в любую степень воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Просто введите число и степень, в которую хотите его возвести, и получите ответ.

Теория

Возведение в степень – это математическая операция, при которой число умножается само на себя энное количество раз в зависимости от значения степени.

Формула

aⁿ=a⋅a⋅a…и так n-раз

Пример

К примеру, возведём число 2 в 3-ю степень:

2³ = 2⋅2⋅2 = 4⋅2 = 8

Как посчитать отрицательную степень

Возведение в отрицательную (минусовую) степень происходит по следующей формуле:

Формула

a^-n = ¹/_aⁿ

Пример

К примеру, возведём число 2 в −3-ю степень:

2^-3 = 1/(2⋅2⋅2) = 1/(4⋅2) = 1/8 = 0,125

Как посчитать дробную степень

Возведение числа в дробную степень происходит по следующей формуле:

Формула

a^ⁿ/_m = ^m√aⁿ

Пример

К примеру, возведём число 4 в степень 0.5:

4^0.5 = 4^½ = ²√4¹ = 2

Теперь пример посложней: возведём число 2 в степень ¾:

2^¾ = ⁴√2³ ≈ 1.6817

См. также

Источник

При помощи нашего калькулятора вы легко сможете возвести число в любую степень.

Что же такое возведение числа в степень? Для того, что бы это понять давайте с вами разберем простой пример:

4³

из которых 4 — это основание, 3 – степень в которую необходимо возвести основание.
Решение данной задачи состоит в следующем

4*4*4 = 64.

Таким образом мы можем сделать простой вывод возведение числа в степень это умножение этого числа на само себя столько раз в какой степени он находиться.

Возводить можно не только в положительную степень, но и в отрицательную. Многие задаются вопросом как возвести в отрицательную степень. При возведении в отрицательную степень надо как обычно возвести число в степень и разделить на него единицу.
Таким образом выражение

4^-3

Записывается следующим образом

1/(4*4*4)= 1/64 = 0,015625

Источник

Калькулятор степеней поможет просто и быстро возвести число в степень онлайн.
При этом показатель степени может быть как положительным, так и отрицательным!

Что такое степень числа?

Как возвести число в степень?

Чтобы понять, как возводить число в степень, рассмотрим несколько простых примеров.

Пример. Вычислить степени и .

Решение.
Возведём в пятую степень число то есть вычислим значение выражения
По определению, данному выше,

$[2^5 = underbrace{2cdot 2cdot 2cdot 2cdot 2}_{5} = 32.]$

Вычислим, чему равно то есть чему равно число возведённое в третью степень:

Отрицательный показатель степени

Показатели степени могут быть не только положительными, но и отрицательными.

$[a^{-n} = frac{1}{a^n}.]$

Например,

$[2^{-3} = frac{1}{2^3} = frac{1}{8},]$

$[5^{-2} = frac{1}{5^2} = frac{1}{25}.]$

Как пользоваться калькулятором степеней

Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные
дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для
отрицательных чисел не определена операция возведения в нецелую степень.

При записи дробных чисел можно использовать как точку, так и запятую. В ответе большие числа записываются в так
называемом «научном формате», то есть число выглядит как <число>e<количество нулей>.
Например, , а

Источник

Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.

Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».

Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.

Как возвести число в степень.

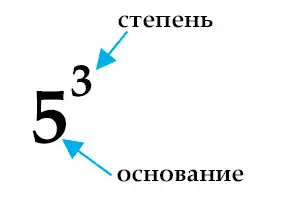
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:

Возведение в степень

А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.

5³ = 5 x 5 x 5 = 125

Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.

Как возводить в отрицательную степень.

При возведении в отрицательную степень необходимо использовать простое правило:

как возводить в отрицательную степень

Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2^-3

мы должны поступить следующим образом:

2^-3 =1 / (2³)

А так как 2³ =8, то мы получим

2^-3 =1 / 8 = 0,125

Ваша оценка

[Оценок: 18313 Средняя: 3.8]

Калькулятор степеней Автор admin средний рейтинг 3.8/5 — 18313 рейтинги пользователей

Источник

Калькулятор степеней онлайн

Онлайн калькулятор степеней вычислит степень как отрицательных, так и положительных чисел. Чтобы записать степень и число можно использовать: целые, десятичные и дробные числа (5, -7, 2.36, 1/2, -4/9). Также для записи степени и основания можно вводить буквенные выражения.

Правила возведения числа в степень

Возведение числа в натуральную степень

Возвести число в целую степень означает умножить число a само на себя n-раз.
Обозначение: aⁿ, где а — основание степени, n — показатель степени.
Например, 4³ = 4 ⋅ 4 ⋅ 4 = 64

Возведение числа в целую степень

Целые числа могут быть как положительными, так и отрицательными. Посмотрим, как возвести число в отрицательную степень.
При первом знакомстве с отрицательной степенью может быть непонятно как, например возвести число 5 в степень -2, выглядит бессмысленно, так как нельзя умножить число 5 само на себя -2 раза.
На такой случай в математике можно применить правило
a^-n = 1 : a^m .
Например, 4^-3 = 1 : 4³ = 0.015625

Возведение числа в дробную степень

Возвести положительное действительное число a в степень m/n, означает извлечь корень n-ой степени из числа a в степени m.
a^m/n = ⁿ√a^m
Например, 6^2/3 = ³√6² = 3.3019272
(2.3)^-2/7 = ⁷√(2.3)^-2 = 0.7882232

Запомните, чтобы возвести число в дробную степень, это число должно быть положительным. Основание a может быть отрицательным только в том случае, если дробная степень не является действительным числом. Поэтому возведение в вещественную степень (положительную или отрицательную) определенно только для a > 0. Для отрицательных чисел в случае вещественной степени в результате вычисления получаются комплексные числа.

Источник