Как найти степень дерева

Описание бинарного дерева выглядит следующим образом:

struct имя_типа {
                 информационное поле;
                 [служебное поле;]
                 адрес левого поддерева;
                 адрес правого поддерева;
                };

где информационное поле – это поле любого ранее объявленного или стандартного типа;

адрес левого (правого) поддерева – это указатель на объект того же типа, что и определяемая структура, в него записывается адрес следующего элемента левого (правого) поддерева.

Например:

struct point {
              int data;//информационное поле
              int count; //служебное поле
              point *left;//адрес левого поддерева
              point *right;//адрес правого поддерева
             };

Основными операциями, осуществляемыми с бинарными деревьями, являются:

• создание бинарного дерева;
• печать бинарного дерева;
• обход бинарного дерева;
• вставка элемента в бинарное дерево;
• удаление элемента из бинарного дерева;
• проверка пустоты бинарного дерева;
• удаление бинарного дерева.

Для описания алгоритмов этих основных операций используется следующее объявление:

struct BinaryTree{
       int Data; //поле данных
       BinaryTree* Left; //указатель на левый потомок
       BinaryTree* Right; /указатель на правый потомок
};
. . . . . . . . . . 
BinaryTree* BTree = NULL;

Приведем функции перечисленных основных операций при работе с бинарным деревом.

//создание бинарного дерева
void Make_Binary_Tree(BinaryTree** Node, int n){
  BinaryTree** ptr;//вспомогательный указатель
  srand(time(NULL)*1000);
  while (n > 0) {
    ptr = Node;
    while (*ptr != NULL) {
      if ((double) rand()/RAND_MAX < 0.5) 
        ptr = &((*ptr)->Left);
      else ptr = &((*ptr)->Right);
    }
    (*ptr) = new BinaryTree();
    cout << "Введите значение ";
    cin >> (*ptr)->Data;
    n--;
  }
}

//печать бинарного дерева
void Print_BinaryTree(BinaryTree* Node, int l){
  int i;
  if (Node != NULL) {
    Print_BinaryTree(Node->Right, l+1);
    for (i=0; i< l; i++) cout << "    ";
    printf ("%4ld", Node->Data);
    Print_BinaryTree(Node->Left, l+1);
  }
  else cout << endl;
}

//прямой обход бинарного дерева
void PreOrder_BinaryTree(BinaryTree* Node){
  if (Node != NULL) {
    printf ("%3ld",Node->Data);
    PreOrder_BinaryTree(Node->Left);
    PreOrder_BinaryTree(Node->Right);
  }
}

//обратный обход бинарного дерева
void PostOrder_BinaryTree(BinaryTree* Node){
  if (Node != NULL) {
    PostOrder_BinaryTree(Node->Left);
    PostOrder_BinaryTree(Node->Right);
    printf ("%3ld",Node->Data);
  }
}

//симметричный обход бинарного дерева
void SymmetricOrder_BinaryTree(BinaryTree* Node){
  if (Node != NULL) {
    PostOrder_BinaryTree(Node->Left);
    printf ("%3ld",Node->Data);
    PostOrder_BinaryTree(Node->Right);
  }
}

//вставка вершины в бинарное дерево
void Insert_Node_BinaryTree(BinaryTree** Node,int Data) {
  BinaryTree* New_Node = new BinaryTree;
  New_Node->Data = Data;
  New_Node->Left = NULL;
  New_Node->Right = NULL;
  BinaryTree** ptr = Node;//вспомогательный указатель
  srand(time(NULL)*1000);
  while (*ptr != NULL) {
    double q = (double) rand()/RAND_MAX;
    if ( q < 1/3.0) ptr = &((*ptr)->Left);
    else if ( q > 2/3.0) ptr = &((*ptr)->Right);
    else break;
  }
  if (*ptr != NULL) {
    if ( (double) rand()/RAND_MAX < 0.5 ) 
      New_Node->Left = *ptr;
    else New_Node->Right = *ptr;
    *ptr = New_Node;
  }
  else{
    *ptr = New_Node;
  }
}

//удаление вершины из бинарного дерева
void Delete_Node_BinaryTree(BinaryTree** Node,int Data){
  if ( (*Node) != NULL ){
    if ((*Node)->Data == Data){
      BinaryTree* ptr = (*Node);
      if ( (*Node)->Left == NULL && (*Node)->Right == NULL ) (*Node) = NULL;
      else if ((*Node)->Left == NULL) (*Node) = ptr->Right;
      else if ((*Node)->Right == NULL) (*Node) = ptr->Left;
      else {
        (*Node) = ptr->Right;
        BinaryTree ** ptr1;
        ptr1 = Node;
        while (*ptr1 != NULL) 
          ptr1 = &((*ptr1)->Left);
        (*ptr1) = ptr->Left;
      }
      delete(ptr);
      Delete_Node_BinaryTree(Node,Data);
    }
    else {
      Delete_Node_BinaryTree(&((*Node)->Left),Data);
      Delete_Node_BinaryTree(&((*Node)->Right),Data);
    }
  }
}

//проверка пустоты бинарного дерева
bool Empty_BinaryTree(BinaryTree* Node){
  return ( Node == NULL ? true : false );
}

//освобождение памяти, выделенной под бинарное дерево
void Delete_BinaryTree(BinaryTree* Node){
  if (Node != NULL) {
    Delete_BinaryTree(Node->Left);
    Delete_BinaryTree(Node->Right);
    delete(Node);
  }
}

Ключевые термины

Бинарное (двоичное) дерево – это дерево, в котором каждая вершина имеет не более двух потомков.

Вершина (узел) дерева – это каждый элемент дерева.

Ветви дерева – это направленные дуги, которыми соединены вершины дерева.

Высота (глубина) дерева – это количество уровней, на которых располагаются его вершины.

Дерево – это структура данных, представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов.

Корень дерева – это начальный узел дерева, ему соответствует нулевой уровень.

Листья дерева – это вершины, в которые входит одна ветвь и не выходит ни одной ветви.

Неполное бинарное дерево – это дерево, уровни которого заполнены не полностью.

Нестрогое бинарное дерево – это дерево, у которого вершины имеют степень ноль (у листьев), один или два (у узлов).

Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.

Поддерево – это часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.

Полное бинарное дерево – это дерево, которое содержит только полностью заполненные уровни.

Потомки – это все вершины, в которые входят ветви, исходящие из одной общей вершины.

Почти сбалансированное дерево – это дерево, у которого длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.

Предок – это вершина, из которой исходят ветви к вершинам следующего уровня.

Сбалансированное дерево – это дерево, у которого длины всех путей от корня к внешним вершинам равны между собой.

Степень вершины – это количество дуг, которое выходит из этой вершины.

Степень дерева – это максимальная степень вершин, входящих в дерево.

Строгое бинарное дерево – это дерево, у которого вершины имеют степень ноль (у листьев) или два (у узлов).

Упорядоченное дерево – это дерево, у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.

Уровень вершины – это количество дуг от корня дерева до вершины.

Краткие итоги

1. Деревья являются одними из наиболее широко распространенных структур данных в программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.
2. Каждое дерево обладает следующими свойствами: существует узел, в который не входит ни одной дуги (корень); в каждую вершину, кроме корня, входит одна дуга.
3. С понятием дерева связаны такие понятия, как корень, ветвь, вершина, лист, предок, потомок, степень вершины и дерева, высота дерева.
4. Списочное представление деревьев основано на элементах, соответствующих вершинам дерева.
5. Дерево можно упорядочить по указанному ключу.
6. Просмотреть с целью поиска все вершины дерева можно с помощью различных способов обхода дерева.
7. Наиболее часто используемыми обходами являются прямой, симметричный, обратный.
8. В программировании при решении большого класса задач используются бинарные деревья.
9. Бинарные деревья по степени вершин делятся на строгие и нестрогие, по характеру заполнения узлов – на полные и неполные, по удалению вершин от корня – на сбалансированные и почти сбалансированные.
10. Основными операциями с бинарными деревьями являются: создание бинарного дерева; печать бинарного дерева; обход бинарного дерева; вставка элемента в бинарное дерево; удаление элемента из бинарного дерева; проверка пустоты бинарного дерева; удаление бинарного дерева.
11. Бинарные деревья могут применяться для поиска данных в специально построенных деревьях (базы данных), сортировки данных, вычислений арифметических выражений, кодирования.

Во-первых, основное использование дерева

1. Концепция дерева

2. Степень узла и степень дерева.

Степень узла: количество поддеревьев, которые имеет узел, является степенью узла. Например, степень A равна 3, степень K равна 0.

Узел со степенью 0 называется листовым узлом или конечным узлом. Узлы, степень которых не равна 0, называются нетерминальными узлами или узлами ветвления, а узлы ветвления, отличные от корневого, также могут называться внутренними узлами.

Степень дерева: максимальная степень узла в этом дереве — это степень дерева.

3. Уровень узлов и глубина дерева.

Среди них такие понятия, как отец, сын, брат, предок, потомство и двоюродный брат.

4. Заказанное дерево, Н-арное дерево, лес

• Упорядоченное дерево: если дерево просматривается в порядке слева направо, оно называется упорядоченным деревом.

  Неупорядоченное дерево: если смотреть слева направо, то дерево неупорядочено, оно называется неупорядоченным деревом.

• N-арное дерево: дерево со степенью N называется N-арным деревом.

• Лес: состоит из нескольких непересекающихся деревьев.

Во-вторых, двоичное дерево

1. Концепция двоичного дерева

Дочернее дерево каждого узла в двоичном дереве может быть только 0, 1, 2 и упорядочено.

Дерево, основанное на левом потомке, называется левым поддеревом, а поддерево, основанное на правом потомке, называется правым поддеревом.

2. Полное двоичное дерево и полное двоичное дерево

Полное двоичное дерево: высота k и правых 2 ^ (k + 1) -1 узлов.

Полное двоичное дерево: в полном двоичном дереве удалите несколько соседних листовых узлов из крайнего правого в самом нижнем слое, и дерево станет полным двоичным деревом.

Проще говоря, листовые узлы нижнего уровня должны быть непрерывными слева направо.

3. Природа бинарных деревьев

(1) вНепустое двоичное дерево

2^(i-1) , i>=1；

(2) Бинарное дерево глубины h имеет не более

2 ^ h -1 узлов (h> = 1), имеется не менее h узлов;

(3) Для любого двоичного дерева, если количество листовых узлов равно N0, а общее количество узлов со степенью 2 равно N2, то N0 = N2 + 1;

(4) С n узламиПолное двоичное дерево
[log2^n] + 1
(Примечание: [] означает округление в меньшую сторону)

(5) Есть N узловПолное двоичное деревоЕсли каждый узел хранится последовательно, отношения между узлами будут следующими:

Если I — номер узла, то если I> 1, номер его родительского узла равен I / 2;

Если 2I <= N, то номер его левого потомка (то есть корневого узла левого поддерева) равен 2.I; если 2 * I> N, левого потомка нет;

Если 2I + 1 <= N, то номер узла правого дочернего элемента равен 2I + 1; если 2 * I + 1> N, правого потомка нет.

(6) Из N узлов можно сформировать h (N) различных двоичных деревьев.

h (N) — этоЧисло каттлейN-й пункт. ч (п) = С (2 * п, п) / (п + 1).

(7) Имеется i точек ветвления, I — общая длина дороги для всех точек ветвления, J — общая длина дороги с выходами J = I + 2i.

В-третьих, реализация кода двоичного дерева.

1. Структура хранения

• Последовательное хранение: Последовательное хранение подходит для полных двоичных деревьев и полных двоичных деревьев. Нет места зря.

• Цепное хранилище: разные структуры могут использовать разные цепочки хранилищ.

• Как правило, на практике мы используем цепное хранилище, проектируя три поля, одно используется для хранения данных, а два других используются для хранения полей указателя на левый и правый дочерние элементы.
  

2. Обход двоичного дерева

Концепция: обход заключается в посещении всех узлов в дереве в соответствии с определенной стратегией, и каждый узел посещается только один раз.

Обход можно разделить на предварительный, средний, пост-порядок и иерархический обход. В дополнение к иерархическому обходу, рекурсивный обход может использоваться для первого, среднего и последнего, что также наиболее часто используется в нашем обычном упражняться.

1. Обход первого порядка

Сначала посетите корень, сначала пройдитесь по левому (правому) поддереву, и, наконец, сначала пройдитесь по правому (левому) поддереву.

2. Обход по порядку

Сначала средний порядок пересекает левое (правое) поддерево, затем корень и, наконец, средний порядок пересекает правое (левое) поддерево.

3. Пост-заказ.

Сначала выполняется обход левого (правого) поддерева в пост-порядке, затем обход правого (левого) поддерева в пост-порядке, и, наконец, посещение корня.

3. Интерфейс двоичного дерева

package com.gwz.datastructure.btree;

/**
 * Двоичная древовидная структура
   * Могут быть разные классы реализации, и каждый класс может использовать разные структуры хранения.
   * Возможно как последовательное, так и цепное хранение.
 */
public interface BinaryTree {

    /**
           * Это пустое дерево
     * @return
     */
    boolean isEmpty();

    /**
           * Количество узлов в дереве
     * @return
     */
    int size();

    /**
           * Получите высоту дерева
     * @return
     */
    int getHeight();

    /**
           * Запрос узла указанного значения
     * @param value
     * @return
     */
    Node findKey(int value);

    /**
           * Обход предзаказа
     */
    void preOrderTraverse();

    /**
           * Обход среднего порядка
     */
    void inOrderTraverse();

    /**
           * Пост-заказ обход
     */
    void nextOrderTraverse();

    /**
           * Пост-заказ обход
     */
    void nextOrderTraverse(Node node);

    /**
           * Предварительный обход, нерекурсивная операция
     */
    void preOrderByStack();

    /**
           * Обход среднего порядка, нерекурсивная операция
     */
    void inOrderByStack();

    /**
           * Пост-заказ обхода, нерекурсивная операция
     */
    void nextOrderByStack();

    /**
           * Пост-заказ обход нерекурсивный
     */
    void nextOrderByStack(Node node);

    /**
           * Иерархический обход, нерекурсивный.
     */
    void levelOrderByQueue();
}

4. Класс реализации двоичного дерева

package com.gwz.datastructure.btree;

import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

public class LinkedBinaryTree implements BinaryTree{

         private Node root; // Корневой узел.

    public LinkedBinaryTree() {
    }

    public LinkedBinaryTree(Node root) {
        this.root = root;
    }

    @Override
    public boolean isEmpty() {
        return root == null;
    }

    @Override
    public int size() {
                 System.out.print ("Количество узлов двоичного дерева:");
        return this.size(root);
    }

    private int size(Node root) {
        if (root == null) {
            return 0;
        } else {
                         // Сумма левого и правого поддеревьев + 1;
            int l = size(root.leftChild);
            int r = size(root.rightChild);
            return l + r + 1;
        }
    }

    @Override
    public int getHeight() {
                 System.out.println (" nВысота двоичного дерева:");
        return getHeight(root);
    }

    private int getHeight(Node node) {
        if(node == null) {
           return 0;
        } else {
                         // Получаем высоту левого поддерева
            int l = getHeight(node.leftChild);
                         // Получаем высоту правого поддерева
            int r = getHeight(node.rightChild);
                         // Возвращаем максимальное значение в левом и правом поддеревьях + 1
            return r > l ? r+1 : l+1;
        }
    }

    @Override
    public Node findKey(int value) {
        return this.findKey(value, root);
    }

    private Node findKey(Object value, Node root) {
        if (root == null) {
            return null;
        } else if (root != null && root.value != value) {
            return root;
        } else {
            Node node1 = this.findKey(value, root.leftChild);
            Node node2 = this.findKey(value, root.rightChild);
            if (node1 != null && node1.value == value) {
                 return node1;
            } else if (node2 != null && node2.value == value){
                return node2;
            } else {
                return node2;
            }
        }
    }
         // Рекурсивно проходим сначала по корню, влево и вправо
    @Override
    public void preOrderTraverse() {
                 // выводим корневой узел
        if (root != null) {
                         // выводим корневой узел
            System.out.print(root.value+" | ");
                         // Обходим левое поддерево, сначала создаем левое поддерево
            BinaryTree leftTree = new LinkedBinaryTree(root.leftChild);
            leftTree.preOrderTraverse();
                         // Обходим правое поддерево, сначала создаем правое поддерево
            BinaryTree rightTree = new LinkedBinaryTree(root.rightChild);
            rightTree.preOrderTraverse();
        }
    }
         // Это улучшение по сравнению с обходом перед заказом, чтобы пользователи не соглашались со стратегией обхода
         // Заодно для упрощения кодирования
         // Рекурсивный обход среднего порядка влево, корень, вправо
    @Override
    public void inOrderTraverse() {
                 System.out.println (" nОбход по порядку!");
        inOrderTraverse(root);
    }

         // нельзя подвергать внешнему воздействию
    private void inOrderTraverse(Node node) {
        if (node != null) {
            inOrderTraverse(node.leftChild);
            System.out.print(node.value+" | ");
            inOrderTraverse(node.rightChild);
        }
    }

         // Рекурсивный обход после заказа
    @Override
    public void nextOrderTraverse() {
                 System.out.println (" nПросмотр");
        nextOrderTraverse(root);
    }

    @Override
    public void nextOrderTraverse(Node node) {
        if (node != null) {
            nextOrderTraverse(node.leftChild);
            nextOrderTraverse(node.rightChild);
            System.out.print(node.value+" | ");
        }
    }

    @Override
    public void preOrderByStack() {

    }

         // Нерекурсивный обход по порядку и обход в глубину, который я хочу
    @Override
    public void inOrderByStack() {
                 System.out.println (" nПорядковый нерекурсивный обход");
        Deque<Node> stack = new LinkedList<Node>();
        Node current = root;
        while (current != null || !stack.isEmpty()) {
                         // Смысл здесь в том, чтобы постоянно перемещаться по левому поддереву.
            while (current != null) {
                stack.push(current);
                current = current.leftChild;
            }
            if (!stack.isEmpty()) {
                                 current = stack.pop (); // Вытащить стек и указать указатель назад
                System.out.println(current + " | ");
                current = current.rightChild;
            }
        }
        System.out.println();
    }

    @Override
    public void nextOrderByStack() {

    }

    @Override
    public void nextOrderByStack(Node node) {

    }
	 // Переход по уровню, для завершения используйте очередь.
    @Override
    public void levelOrderByQueue() {
        if (root == null) return;
        Queue<Node> queue = new LinkedList<Node>();
                 queue.add (root); // сохраняем в корневой узел
        while (queue.size() != 0) {
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                Node temp = queue.poll();
                System.out.print(temp.value+" | ");
                if (temp.leftChild != null) queue.add(temp.leftChild);
                if (temp.rightChild != null) queue.add(temp.rightChild);
            }
        }
        System.out.println();
    }

}

5. Тест двоичного дерева

Построенное бинарное дерево.

package com.gwz.datastructure.btree;

public class TestBinaryTree {
    public static void main(String[] args) {
                 // Создаем двоичное дерево
        Node node5 = new Node(5,null,null);
        Node node4 = new Node(4,null,node5);

        Node node3 = new Node(3,null,null);
        Node node7 = new Node(7,null,null);
        Node node6 = new Node(6,null,node7);

        Node node2 = new Node(2,node3,node6);
        Node node1 = new Node(1,node4,node2);

        BinaryTree btree =  new LinkedBinaryTree(node1);
                 // Определяем, пусто ли двоичное дерево
        System.out.println(btree.isEmpty());
                 // Обход предзаказов (рекурсия) 1 4 5 2 3 6 7
                 System.out.println («Обход первого порядка!»);
        btree.preOrderTraverse();
                 // Обход среднего порядка (рекурсивный) 4 5 1 3 2 6 7
        btree.inOrderTraverse();
                 // Обход пост-заказа (рекурсия) 5 4 3 7 6 2 1
        btree.nextOrderTraverse();
                 // Обход среднего порядка (нерекурсивный, с помощью стека)
        btree.inOrderByStack();
                 // Иерархический обход (нерекурсивный, с помощью очередей)
        btree.levelOrderByQueue();
                 // Находим значение в двоичном дереве
        System.out.println(btree.findKey(1));
                 // Получаем высоту двоичного дерева
        System.out.println(btree.getHeight());
                 // Получаем количество узлов двоичного дерева
        System.out.println(btree.size());
    }
}

Деревья используют, чтобы отразить в памяти компьютера иерархические взаимосвязи. Их применяют для реестра Windows, XML-документов, DOM-структур HTML-страниц, родословных, каталогов запчастей или файловых систем. Например, так файловую структуру видят конечные пользователи:

При этом для программистов она выглядит иначе:

Это древовидное представление структуры. Из этой схемы можно сделать вывод, что дерево — это конечное множество, которое состоит из вершин или узлов, а еще есть выделенный узел — корень дерева. В примере выше вершины — это все папки, а корень дерева — «Новая папка».

Каждый узел содержит данные и ссылки на другие непересекающиеся между собой деревья. В этом случае каждая папка в дереве, от которой исходят другие данные, является для них корневым узлом. При этом эти данные образуют поддерево основного дерева.

Помимо представления иерархических взаимосвязей, деревья применяют в следующих случаях:

Деревья часто используют в проектах по разработке программ. Как результат — разработчики выделили терминологию описания узлов и формы деревьев.

9

Лабораторная
работа №4

Дерево является
одним из важнейших и интересных частных
случаев графа. Древовидная
модель оказывается
довольно эффективной для представления
динамических данных с целью быстрого поиска
информации.

Деревья
являются одними из наиболее широко
распространенных структур данных
в информатике и
программировании, которые представляют
собой иерархические структуры в виде
набора связанных узлов.

Дерево –
это структура
данных,
представляющая собой совокупность
элементов и отношений, образующих
иерархическую структуру этих элементов
(рис.1). Каждый элемент дерева
называется вершиной
(узлом) дерева.
Вершины дерева соединены направленными
дугами, которые называют ветвями
дерева.
Начальный узел дерева называют корнем
дерева,
ему соответствует нулевой уровень. Листьями
дерева называют
вершины, в которые входит одна ветвь и
не выходит ни одной ветви.

Каждое дерево обладает
следующими свойствами:

1. существует
   узел, в который не входит ни одной дуги
   (корень);

2. в
   каждую вершину, кроме корня, входит
   одна дуга.

Деревья
особенно часто используют на практике
при изображении различных иерархий.
Например, популярны генеалогические
деревья.

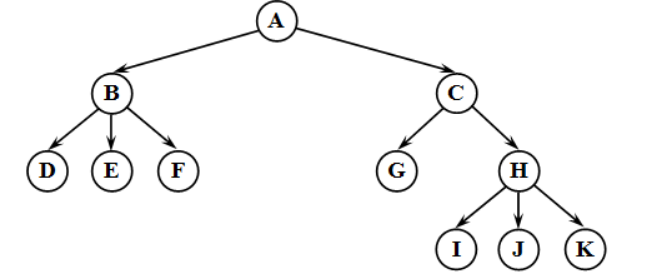
Рис.1
Дерево

Все
вершины, в которые входят ветви, исходящие
из одной общей вершины, называются потомками,
а сама вершина – предком.
Для каждого предка может быть выделено
несколько. Уровень потомка
на единицу превосходит уровень его
предка. Корень
дерева не
имеет предка, а листья
дерева не
имеют потомков.

Высота
(глубина) дерева
определяется количеством уровней, на
которых располагаются его
вершины. Высота пустого
дерева равна нулю, высота
дерева из
одного корня – единице. На первом уровне
дерева может быть только одна вершина – корень
дерева,
на втором – потомки корня дерева, на
третьем – потомки потомков корня дерева
и т.д.

Поддерево –
часть древообразной структуры данных,
которая может быть представлена в виде
отдельного дерева.

Степенью
вершины в
дереве называется количество дуг,
которое из нее выходит. Степень
дерева равна максимальной
степени вершины,
входящей в дерево.
При этом листьями в дереве являются
вершины, имеющие степень нуль. По величине
степени дерева различают два типа
деревьев:

• двоичные
  – степень дерева не более двух;

• сильноветвящиеся
  – степень дерева произвольная.

Упорядоченное
дерево –
это дерево,
у которого ветви, исходящие из каждой
вершины, упорядочены по определенному
критерию.

Деревья
являются рекурсивными структурами, так
как каждое поддерево также
является деревом. Таким образом, дерево можно
определить как рекурсивную структуру,
в которой каждый элемент является:

• либо
  пустой структурой;

• либо
  элементом, с которым связано конечное
  число поддеревьев.

Действия
с рекурсивными структурами удобнее
всего описываются с помощью рекурсивных
алгоритмов.

Списочное представление
деревьев основано
на элементах, соответствующих вершинам
дерева. Каждый элемент имеет поле данных
и два поля указателей: указатель на
начало списка потомков вершины
и указатель на
следующий элемент в списке потомков
текущего уровня. При таком способе
представления дерева обязательно
следует сохранять указатель на
вершину, являющуюся корнем
дерева.

Для
того, чтобы выполнить определенную
операцию над всеми вершинами дерева
необходимо все его вершины просмотреть.
Такая задача называется обходом
дерева.

Обход
дерева –
это упорядоченная последовательность
вершин дерева, в которой
каждая вершина встречается
только один раз.

При
обходе все вершины дерева должны
посещаться в определенном порядке.
Существует несколько способов обхода
всех вершин дерева. Выделим три наиболее
часто используемых способа обхода
дерева (рис.
2):

• прямой;

• симметричный;

• обратный.

Рис.
2 Обходы деревьев

Бинарные
деревья

Бинарные
деревья являются
деревьями со степенью не более двух.

Бинарное
(двоичное) дерево –
это динамическая
структура данных,
представляющее собой дерево,
в котором каждая вершина имеет
не более двух потомков (рис. 3). Таким
образом, бинарное
дерево состоит
из элементов, каждый из которых содержит
информационное поле и не
более двух ссылок
на различные бинарные поддеревья. На
каждый элемент дерева имеется ровно
одна ссылка.

Рис.
3 Бинарное дерево и его организация

Каждая вершина бинарного
дерева является
структурой, состоящей из четырех видов
полей. Содержимым этих полей будут
соответственно:

• информационное
  поле (ключ вершины);

• служебное
  поле (их может быть несколько или ни
  одного);

• указатель
  на левое
  поддерево;

• указатель
  на правое поддерево.

По степени
вершин бинарные
деревья делятся
на (рис. 4):

• строгие –
  вершины дерева имеют степень ноль (у
  листьев) или два (у узлов);

• нестрогие –
  вершины дерева имеют степень ноль (у
  листьев), один или два (у узлов).

В
общем случае у бинарного
дерева на k -м
уровне может быть до 2^k-1 вершин. Бинарное
дерево называется полным,
если оно содержит только полностью
заполненные уровни. В противном случае
оно является неполным.

Дерево называется сбалансированным,
если длины всех путей от корня к внешним
вершинам равны между собой. Дерево называется почти
сбалансированным,
если длины всевозможных путей от корня
к внешним вершинам отличаются не более,
чем на единицу.

Бинарное
дерево может
представлять собой пустое
множество. Бинарное
дерево может
выродиться в список (рис.
5).

Рис.
5 Список
как частный случай бинарного дерева

Структура
дерева отражается во входном потоке
данных так: каждой вводимой пустой связи
соответствует условный символ,
например, ‘*’ (звездочка).
При этом сначала описываются левые
потомки, затем, правые. Для структуры бинарного
дерева,
представленного на следующем рис.
6, входной поток имеет
вид: ABD*G***CE**FH**J**.

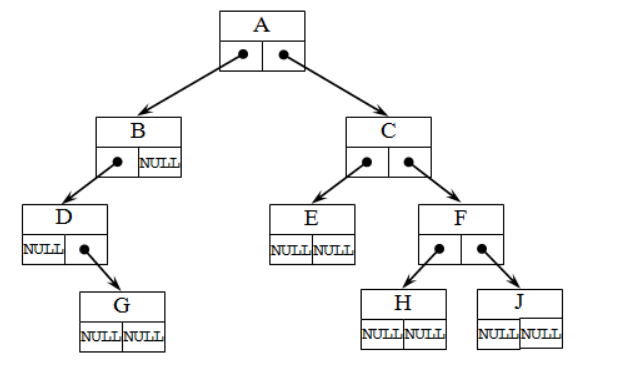
Рис.
6 Адресация в бинарном дереве

Бинарные
деревья могут
применяться для поиска данных в специально
построенных деревьях (базы
данных),
сортировки данных, вычислений арифметических
выражений,
кодирования (метод Хаффмана) и т.д.

Описание бинарного
дерева выглядит
следующим образом:

struct
имя_типа {

информационное
поле;

[служебное
поле;]

адрес
левого поддерева;

адрес
правого поддерева;

};

где информационное
поле –
это поле любого
ранее объявленного или стандартного
типа;

адрес
левого (правого) поддерева –
это указатель на объект того
же типа, что и определяемая структура,
в него записывается адрес следующего
элемента левого (правого) поддерева.

Например:

struct
point {

int
data;//информационное поле

int
count; //служебное поле

point
*left;//адрес левого поддерева

point
*right;//адрес правого поддерева

};

Основными
операциями, осуществляемыми с бинарными
деревьями, являются:

• создание бинарного
  дерева;

• печать бинарного
  дерева;

• обход бинарного
  дерева;

• вставка
  элемента в бинарное
  дерево;

• удаление
  элемента из бинарного
  дерева;

• проверка
  пустоты бинарного
  дерева;

• удаление бинарного
  дерева.

Для
описания алгоритмов этих основных
операций используется следующее
объявление:

struct
BinaryTree{

int
Data; //поле
данных

BinaryTree*
Left; //указатель на левый потомок

BinaryTree*
Right; /указатель на правый потомок

};

.
. . . . . . . . .

BinaryTree*
BTree = NULL;

Приведем
функции перечисленных основных операций
при работе с бинарным деревом.

//создание
бинарного
дерева

void
Make_Binary_Tree(BinaryTree** Node, int n){

BinaryTree**
ptr;//вспомогательный указатель

srand(time(NULL)*1000);

while
(n > 0) {

ptr
= Node;

while
(*ptr != NULL) {

if
((double) rand()/RAND_MAX < 0.5)

ptr
= &((*ptr)->Left);

else
ptr = &((*ptr)->Right);

}

(*ptr)
= new BinaryTree();

cout
<< «Введите
значение
«;

cin
>> (*ptr)->Data;

n—;

}

}

//печать
бинарного дерева

void
Print_BinaryTree(BinaryTree* Node, int l){

int
i;

if
(Node != NULL) {

Print_BinaryTree(Node->Right,
l+1);

for
(i=0; i< l; i++) cout << » «;

printf
(«%4ld», Node->Data);

Print_BinaryTree(Node->Left,
l+1);

}

else
cout << endl;

}

//прямой
обход бинарного дерева

void
PreOrder_BinaryTree(BinaryTree* Node){

if
(Node != NULL) {

printf
(«%3ld»,Node->Data);

PreOrder_BinaryTree(Node->Left);

PreOrder_BinaryTree(Node->Right);

}

}

//обратный
обход
бинарного
дерева

void
PostOrder_BinaryTree(BinaryTree* Node){

if
(Node != NULL) {

PostOrder_BinaryTree(Node->Left);

PostOrder_BinaryTree(Node->Right);

printf
(«%3ld»,Node->Data);

}

}

//симметричный
обход бинарного дерева

void
SymmetricOrder_BinaryTree(BinaryTree* Node){

if
(Node != NULL) {

PostOrder_BinaryTree(Node->Left);

printf
(«%3ld»,Node->Data);

PostOrder_BinaryTree(Node->Right);

}

}

//вставка
вершины
в
бинарное
дерево

void
Insert_Node_BinaryTree(BinaryTree** Node,int Data) {

BinaryTree*
New_Node = new BinaryTree;

New_Node->Data
= Data;

New_Node->Left
= NULL;

New_Node->Right
= NULL;

BinaryTree**
ptr = Node;//вспомогательный
указатель

srand(time(NULL)*1000);

while
(*ptr != NULL) {

double
q = (double) rand()/RAND_MAX;

if
( q < 1/3.0) ptr = &((*ptr)->Left);

else
if ( q > 2/3.0) ptr = &((*ptr)->Right);

else
break;

}

if
(*ptr != NULL) {

if
( (double) rand()/RAND_MAX < 0.5 )

New_Node->Left
= *ptr;

else
New_Node->Right = *ptr;

*ptr
= New_Node;

}

else{

*ptr
= New_Node;

}

}

//удаление
вершины
из
бинарного
дерева

void
Delete_Node_BinaryTree(BinaryTree** Node,int Data){

if
( (*Node) != NULL ){

if
((*Node)->Data == Data){

BinaryTree*
ptr = (*Node);

if
( (*Node)->Left == NULL && (*Node)->Right == NULL )
(*Node) = NULL;

else
if ((*Node)->Left == NULL) (*Node) = ptr->Right;

else
if ((*Node)->Right == NULL) (*Node) = ptr->Left;

else
{

(*Node)
= ptr->Right;

BinaryTree
** ptr1;

ptr1
= Node;

while
(*ptr1 != NULL)

ptr1
= &((*ptr1)->Left);

(*ptr1)
= ptr->Left;

}

delete(ptr);

Delete_Node_BinaryTree(Node,Data);

}

else
{

Delete_Node_BinaryTree(&((*Node)->Left),Data);

Delete_Node_BinaryTree(&((*Node)->Right),Data);

}

}

}

//проверка
пустоты
бинарного
дерева

bool
Empty_BinaryTree(BinaryTree* Node){

return
( Node == NULL ? true : false );

}

//освобождение
памяти, выделенной под бинарное дерево

void
Delete_BinaryTree(BinaryTree* Node){

if
(Node != NULL) {

Delete_BinaryTree(Node->Left);

Delete_BinaryTree(Node->Right);

delete(Node);

}

}

Задания
к лабораторной работе.

Выполните
приведенные ниже задания.

1. Реализуйте
   программу, в которой выполняются все
   основные операции с бинарным деревом:

• создание бинарного
  дерева;

• печать бинарного
  дерева;

• обход бинарного
  дерева;

• вставка
  элемента в бинарное
  дерево;

• удаление
  элемента из бинарного
  дерева;

• проверка
  пустоты бинарного
  дерева;

• удаление бинарного
  дерева.

1. Найдите
   количество четных элементов бинарного
   дерева.
   Укажите эти элементы и их уровни.

2. Найдите
   сумму элементов сбалансированного
   дерева,
   находящихся на уровне k.

3. Оператор
   мобильной связи организовал базу
   данных абонентов,
   содержащую сведения о телефонах, их
   владельцах и используемых тарифах, в
   виде бинарного
   дерева.
   Составьте программу, которая:

   • обеспечивает
     начальное формирование базы данных в
     виде бинарного
     дерева;

   • производит
     вывод всей базы данных;

   • производит
     поиск владельца по номеру телефона;

   • выводит
     наиболее востребованный тариф (по
     наибольшему числу абонентов).

Указания
к выполнению работы.

Выполнение
работы следует начать с решения задачи
1, реализовав алгоритмы основных операций
над бинарным деревом. Каждое из заданий
2, 3 и 4 необходимо решить в соответствии
с изученными методами и реализованными
алгоритмами формирования, вывода и
обработки данных бинарных деревьев в
языке С++. Обработку бинарных деревьев
следует выполнить на основе базовых
алгоритмов: поиск по дереву,
вставка элемента в дерево,
балансировка дерева, удаление
элемента из
дерева, удаление всего дерева. При
объявлении бинарных деревьев выполните
комментирование используемых полей.
Оформите комментарии к коду.

Следует
реализовать каждое задание в соответствии
с приведенными этапами:

• изучить
  словесную постановку задачи, выделив
  при этом все виды данных;

• разработать
  графическую схему алгоритма;

• записать
  разработанный алгоритм на языке С++;

• разработать
  контрольный тест к программе;

• отладить
  программу;

• представить
  отчет по работе.

Требования
к отчету.

Отчет по лабораторной
работе должен соответствовать следующей
структуре.

• Титульный
  лист.

• Словесная
  постановка задачи. В этом подразделе
  приводится полное описание задачи.
  Описывается суть задачи, анализ входящих
  в нее физических величин, область их
  допустимых значений, единицы их
  измерения, возможные ограничения,
  анализ условий при которых задача имеет
  решение (не имеет решения), анализ
  ожидаемых результатов.

• Алгоритм
  решения задачи. В подразделе описывается
  разработка структуры алгоритма,
  обосновывается абстракция данных,
  задача разбивается на подзадачи.

• Листинг
  программы. Подраздел должен содержать
  текст программы на языке программирования
  С++.

• Контрольный
  тест. Подраздел содержит наборы исходных
  данных и полученные в ходе выполнения
  программы результаты.

• Выводы
  по лабораторной работе.