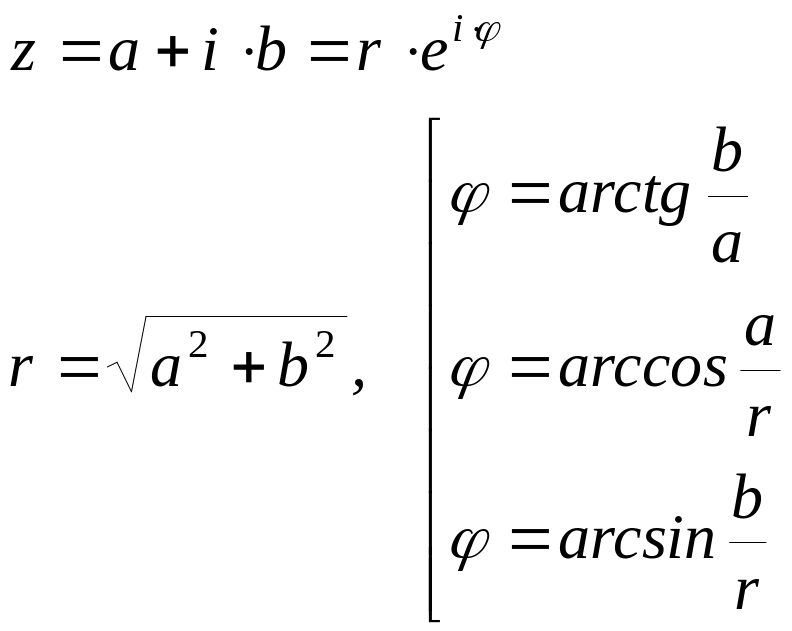Извлечение корня из комплексного числа
30 ноября 2021
Третий урок по комплексным числам. В этом уроке вы узнаете:
- Определение комплексного корня;
- Основная формула — как извлекать корни;
- Геометрическая интерпретация;
- Почему корней всегда ровно n;
- Краткие выводы — если лень читать урок.:)
Начнём с ключевого определения.
1. Определение комплексного корня
Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb{N}$, $n gt 1$, называется такое комплексное число $omega $, что
[{{omega }^{n}}=z]
т.е. $n$-я степень числа $omega $ равна $z$.
Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:
[omega =sqrt[n]{z}]
Пример. Вычислить $sqrt[3]{-1}$ на множестве комплексных чисел.
Очевидно, привычная нам единица является таким корнем, потому что ${{left( -1 right)}^{3}}=-1$. Но есть ещё два корня:
[begin{align} {{left( frac{1}{2}+icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos frac{pi }{3}+icdot sin frac{pi }{3} right) right)}^{3}}= \ & =1cdot left( cos pi +isin pi right)=-1 \ {{left( frac{1}{2}-icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos left( -frac{pi }{3} right)+icdot sin left( -frac{pi }{3} right) right) right)}^{3}}= \ & =1cdot left( cos left( -pi right)+isin left( -pi right) right)=-1 end{align}]
Итого три корня. Как и предполагалось.
Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$
Все эти корни считаются по следующей формуле.
2. Формула корней
Теорема. Пусть комплексное число записано в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Тогда все корни степени $n$ из этого числа можно найти по формуле:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0,1,2,…,n-1 right} \ end{align}]
По сути, эта теорема является обратной к формуле Муавра:
[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos nvarphi +isin n varphi right)]
Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:
- Перевести комплексное число в тригонометрическую форму;
- Записать общую формулу корня степени $n$;
- Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
- Получим $n$ комплексных корней. Вместе они и будут ответом.
В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.
Пример. Вычислить $sqrt[3]{-8i}$.
Представим число $-8i$ в тригонометрической форме:
[begin{align} -8i &=0+left( -8 right)cdot i= \ & =8cdot left( 0+left( -1 right)cdot i right)= \ & =8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right) end{align}]
Запишем формулу корней в общем виде:
[begin{align} sqrt[3]{-8i} & =sqrt[3]{8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right)}= \ & =sqrt[3]{8}cdot left( cos frac{-frac{pi }{2}+2pi k}{3}+isin frac{-frac{pi }{2}+2pi k}{3} right)= \ & =2cdot left( cos left( -frac{pi }{6}+frac{2pi k}{3} right)+isin left( -frac{pi }{6}+frac{2pi k}{3} right) right) \ end{align}]
Подставим $k=0$:
[sqrt[3]{-8i}=2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right)=sqrt{3}-i]
Подставим $k=1$:
[sqrt[3]{-8i}=2cdot left( cos frac{pi }{2}+isin frac{pi }{2} right)=2i]
И, наконец, $k=2$:
[sqrt[3]{-8i}=2cdot left( cos frac{7pi }{6}+isin frac{7pi }{6} right)=-sqrt{3}-i]
В ответе нужно указать все три числа: $2i$; $sqrt{3}-i$; $-sqrt{3}-i$.
Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left{ 0,1,…,n-1 right}$, то корни начнут повторяться, и ничего нового мы не получим.
3. Геометрическая интерпретация
Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n]{left| z right|}$. Более того: эти точки образуют правильный $n$-угольник.
Отметить на комплексной плоскости все числа вида $sqrt[3]{i}$.
Представим число $z=i$ в тригонометрической форме:
[begin{align} z & =1cdot left( 0+icdot 1 right)= \ & =1cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) end{align}]
Формула комплексных корней:
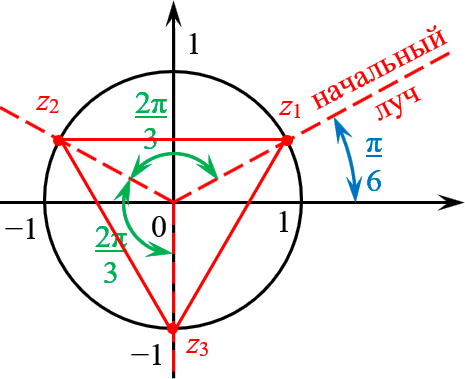
[sqrt[3]{z}=1cdot left( cos left( frac{pi }{6}+frac{2pi k}{3} right)+isin left( frac{pi }{6}+frac{2pi k}{3} right) right)]
Это три точки ${{z}_{1}}$, ${{z}_{2}}$ и ${{z}_{3}}$ на окружности радиуса $R=1$:
Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол ${pi }/{6};$.
Рассмотрим более сложный пример:
Отметить на комплексной плоскости все числа вида $sqrt[4]{1+i}$.
Сразу запишем формулу корней с выделением начального луча:
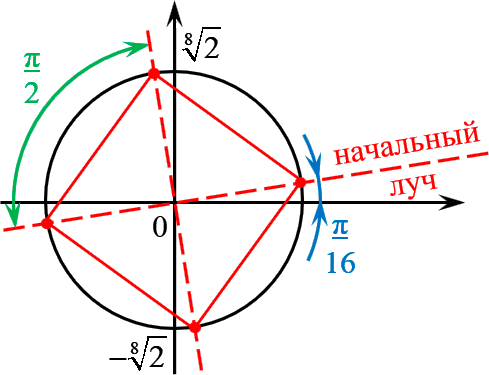
[sqrt[4]{z}=sqrt[8]{2}cdot left( cos left( frac{pi }{16}+frac{pi k}{2} right)+isin left( frac{pi }{16}+frac{pi k}{2} right) right)]
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8]{2}$, начальный луч ${pi }/{16};$:
И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча ${pi }/{16};$.
Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:
Отметить на комплексной плоскости все числа вида $sqrt[6]{-64}$.
Формула корней с выделением начального луча:
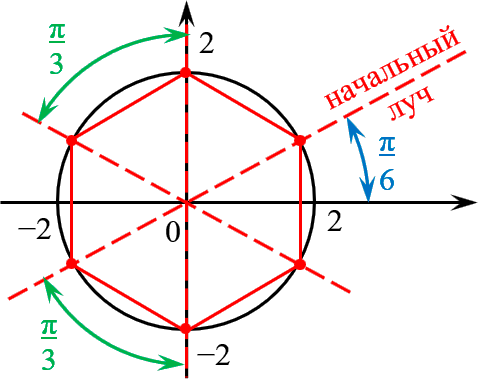
[sqrt[6]{z}=2cdot left( cos left( frac{pi }{6}+frac{pi k}{3} right)+isin left( frac{pi }{6}+frac{pi k}{3} right) right)]
Получили правильный шестиугольник со стороной 2 и начальным лучом ${pi }/{6};$.
Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:
- Перевести число в тригонометрическую форму;
- Найти модуль корня: $sqrt[n]{left| z right|}$ — это будет радиусом окружности;
- Построить начальный луч с отклонением $varphi ={arg left( z right)}/{n};$;
- Построить все остальные лучи с шагом ${2pi }/{n};$;
- Получим точки пересечения лучей с окружностью — это и есть искомые корни.
Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде ${pi }/{6};$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)
4. Почему корней всегда ровно n
С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.
Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]
Последовательно подставим в эту формулу указанные значения параметра $k$:
[begin{align} {{omega }_{0}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right) \ {{omega }_{1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi }{n}+isin frac{varphi +2pi }{n} right) \ & … \ {{omega }_{n-1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi cdot left( n-1 right)}{n}+isin frac{varphi +2pi cdot left( n-1 right)}{n} right) \ end{align}]
Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:
[begin{align} {{omega }_{n}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi n}{n}+isin frac{varphi +2pi n}{n} right)= \ & =sqrt[n]{left| z right|}cdot left( cos left( frac{varphi }{n}+2pi right)+isin left( frac{varphi }{n}+2pi right) right)= \ & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right)={{omega }_{0}} \ end{align}]
Поскольку синус и косинус — периодические функции с периодом $2pi $, ${{omega }_{n}}={{omega }_{0}}$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.
5. Выводы
Ключевые факты из урока.
Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что ${{omega }^{n}}=z$.
Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n]{z}$.
Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.
Алгоритм нахождения корней состоит из двух шагов.
Шаг 1. Представить исходное число в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Шаг 2. Воспользоваться формулой Муавра для вычисления корней:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]
Все полученные корни лежат на окружности радиуса $sqrt[n]{left| z right|}$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол ${varphi }/{n};$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.
Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».
Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)
Смотрите также:
- Тригонометрическая форма комплексного числа
- Системы линейных уравнений: основные понятия
- Радианная мера угла
- Как представить обычную дробь в виде десятичной
- Задача B2 на проценты: железнодорожные билеты
- Логарифмические уравнения в задаче C1
Алгебра и начала математического анализа, 11 класс
Урок №41. Извлечение корня из комплексного числа.
Перечень вопросов, рассматриваемых в теме
1) понятие корня из комплексного числа;
2) алгоритмы извлечения корня из комплексного числа;
3) пример извлечения корня из комплексного числа в тригонометрической форме.
Глоссарий по теме
Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через 
Теорема. Уравнение zn=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.
Все n корней zk лежат на оркужности радиусом 

Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через 
Теорема. Уравнение zn=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.
Доказательство. Пусть ω=|ω|∙(cosφ+isinφ), число z будем искать в виде
z=|z|∙(cosα+isinα).
Преобразуем уравнение zn=ω, используя формулу Муавра:
|z|n(cosnζ+isinnζ)=|ω|∙(cosθ+isinθ).
Отсюда вытекают равенства:
|z|n=|ω|, nζ= θ+2πk, k- целое,
Из которых для модуля искомого корня получается определенное значение 

Таким образом, число различных значений корня равно n- это

Все n корней zk лежат на оркужности радиусом 

Пример 1. Найдите все корни n-ой степени из действительного числа x>0.
Решение. Если х- положительное действительное число, то |x|=x, θ=arg x=0. Формула корней в этом случае дает ответ:

При k=0 получим 
Корни n-ой степени из 1 часто обозначают через εk, k= 0, 1, 2, …, n-1. Согласно предыдущему примеру:
Пример 2. Вычислите корни третьей степени из комплексного числа 2+2i.
Решение: Найдем тригонометрическую форму данного числа:
По формуле корней из комплексного числа имеем:

Используя формулы для косинуса и синуса разности углов, получаем:
Ответ: 

Немного иначе извлекаются корни из комплексных чисел, аргумент которых не приводится к виду 
Пример 3. Найдите
Решение. Пусть ω=3+4i. Положим φ=arg ω.



Следовательно, 
Запишем подробнее:
Найдем 








Ответ:
Пример 4. Выполнить операцию извлечения корня z3 для заданных комплексных чисел в алгебраической форме представления: 
Решение: Тригонометрическая форма записи некоторого комплексного числа имеет вид z=r(cosφ+i⋅sinφ). По условию 
Вычислим аргумент исходного комплексного числа, используя формулу (*):

Для k=0 получаем:
Для k=1 получим:
Для k=2 получим:
Разбор решения заданий тренировочного модуля
№1. Тип задания: множественный выбор
Найдите
Выберите верные ответы из предложенных:
- 2+i
- -2+i
- -2-i
- 2-i
Решение. Пусть ω=3-4i. Положим φ=arg ω.



Следовательно, 
Запишем подробнее:
Найдем 








Ответ: 2+i; -2-i
Верные ответы: 1, 3
№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Чему будет равно произведение: (5 + 3i)∙(1 — 2i)=______
Решение:
((5 + 3i) · (1 — 2i) = 5·1 — 5·2i + 3·1i — 3·2i2 = 5 — 10i + 3i + 6 =11 — 7i
Ответ: 11-7i
-
Возведение
комплексного числа в целую положительную
степень Формула Муавра
в алгебраической
форме zn=(а+i·b)n
– по формулам сокращенного умножения;
в тригонометрической
форме
[r(cos+isin)]n=rn(cosn+isinn).
при возведении
комплексного числа (в
тригонометрической форме)
в целую положительную степень модуль
возводится в эту степень, а аргумент
умножается на показатель степени.
-
Извлечение корня
n-ой
из комплексного числа
в алгебраической
форме не
представляется возможным;
в тригонометрической
форме
Определение:
Корнем п-й
степени
из
комплексного числа называется такое
комплексное число, п-я
степень которого
равняется подкоренному числу, т. е.

Придавая k
значения 0,
1, 2, …, n-1,
получим n
различных значений корня. Для других
значений k
аргументы
будут отличаться от полученных на число,
кратное 2,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень n-й
степени из комплексного числа имеет n
различных значений.
Корень n-й
степени из действительного числа А,
отличного
от нуля, также имеет п
значений, так
как действительное число является
частным случаем комплексного и может
быть представлено в тригонометрической
форме:
A=|A|(cos0+isin0)
при А>0,
A=|A|(cos+isin)
при А<0.
Например:
Вычислить
все корни третьей степени из комплексного
числа z=-3-3i.

Например:
Вычислить
все корни второй степени из комплексного
числа z=-9.

Комплексные числа
b=0
a=0
Комплексные числа и действия над ними.
|
В алгебраической z1=а1+i·b1; z2=а2+i·b2; |
В тригонометрической z1=r1·(cos1+i·sin1); z2=r2·(cos2+i·sin2); |
В показательной z1=r1·еi·1; z2=r2·еi·2; |
|
|
− |
|
|
|
|
Сложение |
z1+z2=(а1+а2)+i·(b1+b2) |
− |
− |
|
Вычитание |
z1—z2=(а1-а2)+i·(b1—b2) |
− |
− |
|
Умножение |
z1z2=(а1а2—b1b2)+i(а2b1+a1b2) |
z1·z2=r1·r2·[cos(1+2)+i·sin(1+2)] |
z1z2=r1·r2·еi·(1+2) |
|
Деление |
|
|
|
|
Возведение в |
zn=(а+i·b)n |
[r·(cos+i·sin)]n=rn·(cos |
[r·еi·]n=rn·еi··n |
|
Извлечение корня |
− |
k=0, |
k=0, |
5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение
Корнем $n$-ой степени из комплексного числа
$z$ называется такое
комплексное число
$w$,
$n$-я степень которого
равна $z$, то есть
$w^{n}=z$
Корень $n$-ой степени из комплексного числа
$z$ обозначается символом
$sqrt[n]{z}$ и на множестве комплексных чисел
имеет ровно $n$ значений.
Если комплексное число $z$ задано в
тригонометрической форме: $z=|z|(cos phi+i sin phi)$, то все значения корня
$n$-ой степени вычисляются по формуле Муавра
(Абрахам де Муавр (1667 — 1754) — английский математик):
$sqrt[n]{z}=sqrt[n]{|z|}left(cos frac{phi+2 n k}{n}+i sin frac{phi+2 n k}{n}right), k=0,1,2, ldots, n-1$
Геометрически все значения корня лежат на окружности радиуса
$sqrt[n]{|z|}$ с центром в начале координат и образуют правильный
$n$-угольник.
Пример
Задание. Вычислить корень четвертой степени из
$z=-1$
Решение. Запишем заданное число в тригонометрической форме, для этого вычислим
модуль и аргумент:
$|z|=|-1|=sqrt{(-1)^{2}+0^{2}}=1$
$arg z=arg (-1)=operatorname{arctg} frac{0}{-1}+pi=operatorname{arctg} 0+pi=0+pi=pi$
То есть
$z=-1=1 cdot(cos pi+i sin pi)=cos pi+i sin pi$
Тогда
$w_{k}=sqrt[4]{z}=sqrt[4]{-1}=sqrt[4]{1} cdotleft(cos frac{pi+2 pi k}{4}+i sin frac{pi+2 pi k}{4}right)=$
$=cos frac{pi+2 pi k}{4}+i sin frac{pi+2 pi k}{4}, k=overline{0 ; 3}$
Отсюда все значения корня:
$k=0 : w_{0}=cos frac{pi}{4}+i sin frac{pi}{4}=frac{sqrt{2}}{2}+frac{sqrt{2}}{2} i$
$k=1 : w_{1}=cos frac{pi+2 pi}{4}+i sin frac{pi+2 pi}{4}=cos frac{3 pi}{4}+i sin frac{3 pi}{4}=$
$=-frac{sqrt{2}}{2}+frac{sqrt{2}}{2} i$
$k=2 : w_{2}=cos frac{pi+4 pi}{4}+i sin frac{pi+4 pi}{4}=cos frac{5 pi}{4}+i sin frac{5 pi}{4}=$
$=-frac{sqrt{2}}{2}-frac{sqrt{2}}{2} i$
$k=3 : w_{3}=cos frac{pi+6 pi}{4}+i sin frac{pi+6 pi}{4}=cos frac{7 pi}{4}+i sin frac{7 pi}{4}=$
$=frac{sqrt{2}}{2}-frac{sqrt{2}}{2} i$
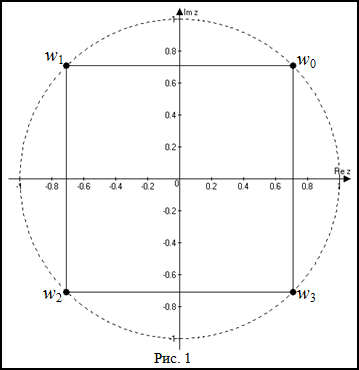
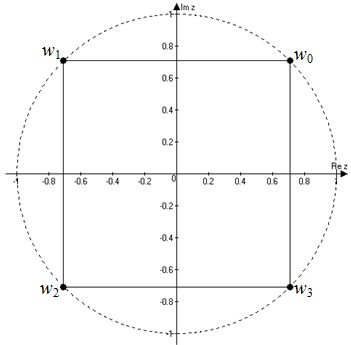
Покажем, что все значения корня лежат на окружности радиуса
$sqrt[4]{|z|}=sqrt[4]{1}=1$ и образуют правильный четырехугольник,
то есть квадрат (рис. 1):
Ответ. $w_{0}=frac{sqrt{2}}{2}+frac{sqrt{2}}{2} i, w_{1}=-frac{sqrt{2}}{2}+frac{sqrt{2}}{2} i, w_{2}=-frac{sqrt{2}}{2}-frac{sqrt{2}}{2} i$
$w_{3}=frac{sqrt{2}}{2}-frac{sqrt{2}}{2} i$
Читать дальше: формула Эйлера для комплексных чисел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Извлечение корня из некоторого комплексного числа выполняется для чисел, которые представлены в тригонометрической форме.
Определение 1
Выражение вида $z=a+bi$, где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=sqrt{-1} $ или $i^{2} =-1$.
Определение 2
Запись некоторого комплексного числа $z$ в следующем виде $z=rcdot (cos varphi +isin varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } $, $varphi $ — аргумент комплексного числа $z$, который определяется по формуле $varphi =arctgfrac{b}{a} $.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 3
Корень $n$-ой степени из некоторого комплексного числа $z$ — это такое комплексное число $w$, $n$-я степень которого равна $z$, то есть [w^{n} =z.]
Примечание 1
Корень $n$-ой степени из некоторого комплексного числа $z$ обозначают как $sqrt[{n}]{z} $; на множестве всех комплексных чисел корень $n$-ой степени из этого комплексного числа $z$ имеет в точности $n$ значений.
Примечание 2
Однозначно извлечь корень из некоторого комплексного числа невозможно, так как он имеет количество значений, равное его степени.
Примечание 3
С геометрической точки зрения все значения корня $n$-ой степени из некоторого комплексного числа $z$ лежат на некоторой окружности радиуса $sqrt[{n}]{z} $, центр которой находится в начале координат О(0;0), и образуют правильный $n$-угольник (рис. 1).
«Извлечение корня из комплексного числа» 👇
Рис. 1
Все комплексные числа, представленные в тригонометрической форме, можно возвести в некоторую степень по формуле Муавра:
[z^{n} =r^{n} cdot (cos nvarphi +isin nvarphi ),, , , , , forall nin N.]
Аналогично применяя формулу Муавра для вычисления корня $n$-ой степени из некоторого комплексного числа $z$ (не равного нулю) получаем:
[sqrt[{n}]{z} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]
Определение 4
Корнем $n$-й степени из некоторого комплексного числа $z=rcdot (cos varphi +isin varphi )$ является комплексное число, которое определяется равенством
[sqrt[{n}]{z} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]
Примечание 4
Если некоторое комплексное число $z$ отлично от нуля, то корень $n$-й степени существует всегда.
Пример 1
Выполнить действие $sqrt[{3}]{z} $, где $z=2cdot (cos pi +icdot sin pi )$.
Решение:
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =sqrt[{3}]{z} =sqrt[{3}]{2} cdot left(cos frac{pi }{3} +icdot sin frac{pi }{3} right)$.
Для $k=1$ получаем: $w_{2} =sqrt[{3}]{z} =sqrt[{3}]{2} cdot left(cos frac{pi +2pi }{3} +icdot sin frac{pi +2pi }{3} right)=sqrt[{3}]{2} cdot left(cos pi +icdot sin pi right)$.
Для $k=2$ получаем: $w_{3} =sqrt[{3}]{z} =sqrt[{3}]{2} cdot left(cos frac{pi +4pi }{3} +icdot sin frac{pi +4pi }{3} right)=sqrt[{3}]{2} cdot left(cos frac{5pi }{3} +icdot sin frac{5pi }{3} right)$.
Определение 5
Запись некоторого комплексного числа $z$ в следующем виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ — вещественная (действительная) часть, обозначение $Rez=a$;
- $b$ — мнимая часть, обозначение $Imz=b$.
Алгоритм 1
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в алгебраической форме, необходимо выполнить следующие действия:
- записать данное число в тригонометрической форме;
- извлечь корни, используя определение.
Алгоритм 2
Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- вычислить модуль и аргумент;
- подставить полученные значения в выражение $z=r(cos varphi +icdot sin varphi )$.
Пример 2
Выполнить операцию извлечения корня $sqrt[{3}]{z} $ для заданных комплексных чисел в алгебраической форме представления:
[z=frac{1}{2} +frac{1}{2} cdot i.]
Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=frac{1}{2} ,b=frac{1}{2} $.
Вычислим модуль исходного комплексного числа:
[r=sqrt{left(frac{1}{2} right)^{2} +left(frac{1}{2} right)^{2} } =sqrt{frac{1}{4} +frac{1}{4} } =sqrt{frac{1}{2} } =frac{sqrt{2} }{2} ]
Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{1/2}{1/2} =arctg1=frac{pi }{4} .]
Подставим полученные значения и получим:
[z=frac{sqrt{2} }{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} ).]
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =sqrt[{3}]{z} =sqrt[{3}]{frac{sqrt{2} }{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.
Для $k=1$ получаем:
[w_{2} =sqrt[{3}]{z} =sqrt[{3}]{frac{sqrt{2} }{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{frac{sqrt{2} }{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right).]
Для $k=2$ получаем:
[w_{3} =sqrt[{3}]{z} =sqrt[{3}]{frac{sqrt{2} }{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{frac{sqrt{2} }{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right).]
Определение 6
Запись комплексного числа $z$ в следующем виде $z=rcdot e^{ivarphi } $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } $, $varphi $ — аргумент комплексного числа $z$, который определяется по формуле $varphi =arctgfrac{b}{a} $.
Алгоритм 3
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в показательной форме, необходимо выполнить следующие действия:
- записать число в тригонометрической форме;
- извлечь корни, используя определение.
Алгоритм 4
Чтобы комплексное число $z$, записанное в показательной форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- определить из показательной записи числа значения модуля и аргумента;
- подставить полученные значения в выражение $z=r(cos varphi +icdot sin varphi )$.
Пример 3
Выполнить операцию извлечения корня $sqrt{z} $ для заданных комплексных чисел в показательной форме представления:
[z=3cdot e^{frac{pi }{3} cdot i} .]
Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
Определим значения модуля и аргумента: $r=3,, , varphi =frac{pi }{3} $.
Запись числа в тригонометрической форме имеет вид: $z=3cdot (cos frac{pi }{3} +isin frac{pi }{3} )$.
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =sqrt{z} =sqrt{3} cdot left(cos frac{pi }{6} +icdot sin frac{pi }{6} right)$.
Для $k=1$ получаем:
[w_{2} =sqrt{z} =sqrt{3} cdot left(cos frac{pi /3+2pi }{2} +icdot sin frac{pi /3+2pi }{2} right)=sqrt{3} cdot left(cos frac{7pi }{6} +icdot sin frac{7pi }{6} right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме