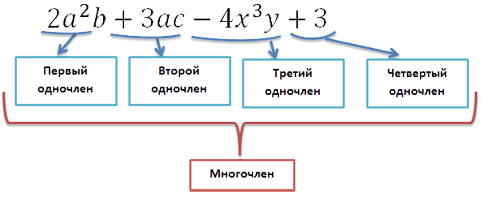
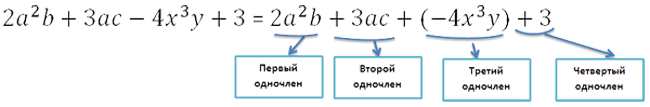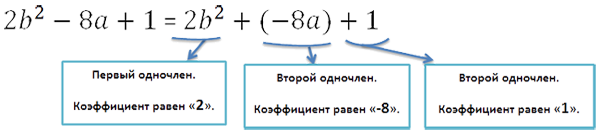Как найти степень многочлена с примером - Исправление недочетов и поиск решений вместе с Examum.ru

Часто путают понятия одночлена и многочлена.

Давайте разберемся, что называют одночленом, а что многочленом.
Прежде всего, вспомним, что называли одночленом в уроке «Одночлены».

Обратите внимание, что «внутри» одночлена (между буквами и числовым коэффициентом) есть только знак умножения.
Например, в одночлене:
3ab = 3 · a · b

Запомните!

Многочленом называется алгебраическая сумма нескольких одночленов.

Одночлены, из которых составлен многочлен, называют членами многочлена.

Примеры многочленов:
a + 2b² − c;
3t⁵ − 4b;
4 − 6xy

Несложно заметить, что любой многочлен состоит из нескольких одночленов.

Рассмотрим многочлен подробнее.

Возникает вопрос, почему многочленом называют алгебраическую сумму
одночленов, если в многочлене присутствует
знак минуса.

Это объясняется тем, что на самом деле знак «−» относится к числовому коэффициенту одночлена,
который стоит справа от знака.

Любой многочлен можно записать
по правилу знаков
как сумму одночленов.

В многочлене знак, который стоит слева от одночлена относится к числовому коэффициенту самого одночлена.

Как найти степень многочлена

Запомните!

Степенью многочлена называют наибольшую из степеней входящих в него одночленов.

То есть, чтобы найти степень многочлена, нужно сначала найти
степень каждого одночлена, который входит в
состав многочлена.

Степени многочленов

Многочлен

Степень
многочлена

a²
− 3a²b
+ x =

a²_{(степень одночлена 2)}
− 3a²b_{(степень одночлена 3)}
+ x_{(степень одночлена 1)}

x²y²
+ 4x² =

x²y²_{(степень одночлена 4)}
+ 4x²_{(степень одночлена 2)}

8x²
− 3a
+ 4 =

8x²_{(степень одночлена 2)}
− 3a_{(степень одночлена 1)}
+ 4_{(степень одночлена 0)}

Любой одночлен является многочленом.
В самом деле, любой одночлен, по сути, является многочленом, который состоит всего из одного одночлена.

Примеры таких многочленов: 2a²b;
−3d³; a.

Число «0» называют нулевым многочленом.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Что такое многочлены? Познакомимся с этим понятием из курса математики 7 класс. Мы с вами дадим определение многочленам, рассмотрим какие выражения можно назвать многочленами, а какие нельзя. Разберем что такое многочлен стандартного вида и степень многочлена и решим несколько примеров на определение степени многочлена и приведение подобных слагаемых.

Определение многочлена

Многочленом называют алгебраическую сумму одночленов. То есть многочлен – это алгебраическое выражение, которое записывается в виде суммы одночленов.

Пример многочлена: .

Неправильно

Как отличить многочлен от не многочлена – обратите внимание на варианты неправильного называния не многочлена многочленом:

Виды многочленов

Среди многочленов выделяют следующие виды многочлены:

Многочлен состоящий из одного одночлена называется одночленом.
Многочлен, состоящий из двух одночленов, называется двучленом или биномом.
Многочлен, состоящий из трех одночленов, называется трехчленом.

Это стандартные называния таких многочленов, многочлен, состоящий из любого произвольного числа одночленов, большего трех, называется просто многочленом.

Стандартный вид многочлена

Если все входящие в многочлен одночлены имеют стандартный вид и в многочлене приведены подобные слагаемые, то такой многочлен называется многочленом стандартного вида.

Приведем пример: выражение является многочленом стандартного вида.

Степень многочлена

Чтобы определить степень многочлена нужно найти одночлен с наибольшей степенью, входящий в его состав. Например, в многочлене наибольшая степень у одночлена , у которого степень 5. Таким образом, и многочлен будет пятой степени.

Сложение подобных слагаемых

Сумму подобных членов многочлена можно заменить одним членом, если сложить их числовые коэффициенты и оставить буквенную часть. Такое сложение или, иначе, тождественное преобразование, называют приведением подобных слагаемых.

Приведем пример: в многочлене можно сложить подобные слагаемые и , тогда мы получим: и .

Многочлен можно записать в виде

Примеры решения задач

Задание 1

Определите степень многочлена .

Решение: наибольшая степень у одночлена , значит, степень многочлена – 3.

Задание 2

Приведите подобные слагаемые многочлена: $underline{a^4} + underline{underline{-3a^2}}+ underline{underline{5a^2}}+ underline{-a^4}$ .

Решение: сложим слагаемые одинаковой степени, это и , а также сложим и . Подчеркнем подобные слагаемые одинаковыми чертами. Получаем, $underline{a^4} + underline{underline{-3a^2}}+ underline{underline{5a^2}}+ underline{-a^4}=2a^2$ .

Ответ: .

Задание 3

Приведите подобные члены многочлена:

Решение: выделим подобные слагаемые и сложим их: $underline{x^4}+underline{underline{a^2}}-underline{6x^4}+underline{underline{7a^2}}=(underline{x^4}-underline{6x^4})+(underline{underline{a^2}}+underline{underline{7a^2}})=-5x^4+8a^2$ .

Ответ: .

Задание 4

Приведите подобные члены многочлена:

Решение: подчеркнем подобные слагаемые и выполним сложение: $underline{3y^3}- underline{underline{ab}}+underline{8y^3}+underline{underline{9ab}}=11y^3+8ab$ .

Ответ: .

Задание 5

Приведите подобные члены многочлена:

Решение: .

Ответ:

Задание 6

Приведите подобные члены многочлена:

Решение: .

Ответ: .

Задание 7

Приведите подобные члены многочлена: .

Решение: .

Ответ: .

Задание 8

Приведите подобные члены многочлена: .

Решение: .

Ответ:

Источник

Download Article

Polynomial means «many terms,» and it can refer to a variety of expressions that can include constants, variables, and exponents. For example, x — 2 is a polynomial; so is 25. To find the degree of a polynomial, all you have to do is find the largest exponent in the polynomial.^[1] If you want to find the degree of a polynomial in a variety of situations, just follow these steps.

1

Combine like terms. Combine all of the like terms in the expression so you can simplify it, if they are not combined already. Let’s say you’re working with the following expression: 3x² — 3x⁴ — 5 + 2x + 2x² — x. Just combine all of the x², x, and constant terms of the expression to get 5x² — 3x⁴ — 5 + x.^[2]
2
Drop all of the constants and coefficients. The constant terms are all of the terms that are not attached to a variable, such as 3 or 5. The coefficients are the terms that are attached to the variable. When you’re looking for the degree of a polynomial, you can either just actively ignore these terms or cross them off. For instance, the coefficient of the term 5x² would be 5. The degree is independent of the coefficients, so you don’t need them.
- Working with the equation 5x² — 3x⁴ — 5 + x, you would drop the constants and coefficients to get x² — x⁴ + x.
Advertisement
3

Put the terms in decreasing order of their exponents. This is also called putting the polynomial in standard form.^[3]. The term with the highest exponent should be first, and the term with the lowest exponent should be last. This will help you see which term has the exponent with the largest value. In the previous example, you would be left with
-x⁴ + x² + x.
4

Find the power of the largest term. The power is simply number in the exponent. In the example, -x⁴ + x² + x, the power of the first term is 4. Since you’ve arranged the polynomial to put the largest exponent first, that will be where you will find the largest term.
5

Identify this number as the degree of the polynomial. You can just write that the degree of the polynomial = 4, or you can write the answer in a more appropriate form: deg (3x² — 3x⁴ — 5 + 2x + 2x² — x) = 4. You’re all done.^[4]
6

Know that the degree of a constant is zero. If your polynomial is only a constant, such as 15 or 55, then the degree of that polynomial is really zero. You can think of the constant term as being attached to a variable to the degree of 0, which is really 1. For example, if you have the constant 15, you can think of it as 15x⁰, which is really 15 x 1, or 15. This proves that the degree of a constant is 0.

1
Write the expression. Finding the degree of a polynomial with multiple variables is only a little bit trickier than finding the degree of a polynomial with one variable. Let’s say you’re working with the following expression:
- x⁵y³z + 2xy³ + 4x²yz²
2
Add the degree of variables in each term. Just add up the degrees of the variables in each of the terms; it does not matter that they are different variables. Remember that the degree of a variable without a written degree, such as x or y, is just one. Here’s how you do it for all three terms:^[5]
- deg(x⁵y³z) = 5 + 3 + 1 = 9
- deg(2xy³) = 1 + 3 = 4
- deg(4x²yz²) = 2 + 1 + 2 = 5
3

Identify the largest degree of these terms. The largest degree of these three terms is 9, the value of the added degree values of the first term.^[6]
4

Identify this number as the degree of the polynomial. 9 is the degree of the entire polynomial. You can write the final answer like this: deg (x⁵y³z + 2xy³ + 4x²yz²) = 9.

1

Write down the expression. Let’s say you’re working with the following expression: (x² + 1)/(6x -2).^[7]
2

Eliminate all coefficients and constants. You won’t need the coefficients or constant terms to find the degree of a polynomial with fractions. So, eliminate the 1 from the numerator and the 6 and -2 from the denominator. You’re left with x²/x.
3

Subtract the degree of the variable in the denominator from the degree of the variable in the numerator. The degree of the variable in the numerator is 2 and the degree of the variable in the denominator is 1. So, subtract 1 from 2. 2-1 = 1.
4

Write the result as your answer. The degree of this rational expression is 1. You can write it like this: deg [(x² + 1)/(6x -2)] = 1.

Add New Question

Question

What is the degree of a polynomial?

In the case of a polynomial with only one variable (such as 2x³ + 5x² — 4x +3, where x is the only variable),the degree is the same as the highest exponent appearing in the polynomial (in this case 3). In the case of a polynomial with more than one variable, the degree is found by looking at each monomial within the polynomial, adding together all the exponents within a monomial, and choosing the largest sum of exponents. That sum is the degree of the polynomial. For example, in the expression 2x²y³ + 4xy² — 3xy, the first monomial has an exponent total of 5 (2+3), which is the largest exponent total in the polynomial, so that’s the degree of the polynomial.
Question

What is degree of 1/x^4 + x^2?

1 / (x^4) is equivalent to x^(-4). So the highest (most positive) exponent in the polynomial is 2, meaning that 2 is the degree of the polynomial.
Question

What about a polynomial with multiple variables that has one or more negative exponents in it?

Combine the exponents found within a given monomial as you would if all the exponents were positive, but you would subtract the negative exponents.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

This just shows the steps you would go through in your mind. You don’t have to do this on paper, though it might help the first time. If you do it on paper, however, you won’t make a mistake.
By convention, the degree of the zero polynomial is generally considered to be negative infinity.
For the third step, linear terms like x can be written as x¹ and non-zero constant terms like 7 can be written as 7x⁰

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find the degree of a polynomial with one variable, combine the like terms in the expression so you can simplify it. Next, drop all of the constants and coefficients from the expression. Then, put the terms in decreasing order of their exponents and find the power of the largest term. The power of the largest term is the degree of the polynomial. To find the degree of a polynomial with multiple variables, write out the expression, then add the degree of variables in each term. The power of the largest term is your answer! If you want to learn how to find the degree of a polynomial in a rational expression, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 873,695 times.

Did this article help you?

Источник

Степень многочлена

Что такое степень многочлена? Как определить степень одночлена?

Определение.

Степенью многочлена называют наибольшую из степеней входящих в него одночленов.

Обычно, прежде чем искать степень многочлена, его приводят к многочлену стандартного вида, хотя, вообще говоря, это не обязательно.

Итак, чтобы найти степень многочлена:

1) Можно привести многочлен к стандартному виду.

2) Найти степень всех входящих в него одночленов — членов многочлена.

3) Выбрать наибольшую из этих степеней.

Примеры.

Найти степень многочлена:

$[1)7{x^2}y - 11xy + 4y - 9;]$

$[2)10{x^2}{y^3} + 32{x^4} - 12{x^2}{y^2};]$

$[3)14a{a^2} - 3{a^3}b + 8ab cdot 2{b^2} - 2{a^3}b;]$

Решение:

$[1)7{x^2}y - 11xy + 4y - 9;]$

Данный многочлен записан в стандартном виде. Степень первого члена многочлена — одночлена 7x²y — равна 2+1=3. Степень второго члена многочлена — -11xy — равна 1+1=2. Степень третьего члена многочлена — 4y — равна 1. -9 — одночлен нулевой степени.

Наибольшая из степеней одночленов — 3. Таким образом, это — многочлен третьей степени.

$[2)10{x^2}{y^3} + 32{x^4} - 12{x^2}{y^2};]$

Здесь 10x²y³ — одночлен 5-й степени, 32x⁴ — 4-й, -12x²y² — также одночлен 4-й степени. Наибольшая из степеней одночленов — 5. Следовательно, это — многочлен 5-й степени.

3) Сначала приведем данный многочлен к стандартному виду:

$[14a{a^2} - 3{a^3}b + 8ab cdot 2{b^2} - 2{a^3}b = ]$

$[ = 14{a^3}underline { - 3{a^3}b} + 16a{b^3}underline { - 2{a^3}b} = ]$

$[ = 14{a^3} - 5{a^3}b + 16a{b^3}.]$

14a³ — одночлен 3-й степени, -5a³b — 4-й, 16ab³ — также одночлен 4-й степени. Наибольшая из степеней входящих в многочлен одночленов — 4. Таким образом, данный многочлен имеет четвертую степень.

Хотя в алгебре принято упрощать многочлен, приводя его к стандартному виду, степень можно искать и для многочлена, не записанного в стандартном виде.

1,7x — одночлен 1-й степени, 2y — одночлен 1-й степени, -12 — одночлен 0-й степени. Значит, это — многочлен первой степени.

Одночлен считают многочленом, состоящим из одного члена. 20 — одночлен 0-й степени. Следовательно, 20 является многочленом нулевой степени.

Источник

Что такое многочлен?

Многочлен – это сумма одночленов. Одночлены, которые составляют многочлен, называют членами данного многочлена. Если многочлены состоят из двух или трех слагаемых, то их можно называть двучленами или трехчленами соответственно.

Пример №1.

–12х⁶+ 35с данный многочлен состоит из двух слагаемых – одночленов, таких как: –12х⁶и 35с. Еще такой многочлен можно называть двучленом.
47с²+11с–34 данный многочлен состоит из трех слагаемых. Такой многочлен можно назвать трехчленом.
4х³+13а²–45с+28 данный многочлен состоит из четырех слагаемых – одночленов, таких как: 4х³; 13а²; – 45с; 28.

Стандартный вид многочлена

Что такое стандартный вид многочлена?

Многочлен называется приведенным к стандартному виду, если он не имеет подобных слагаемых, и каждый его член имеет также стандартный вид.

Вспомним, что слагаемые, содержащие одинаковую буквенную часть или не имеющие буквенной части называют подобными. Если такие слагаемые есть, то их нужно сложить или вычесть, это действие называют приведением подобных слагаемых.

Пример №2.

13х²–6х+11х²

Данный трехчлен имеет подобные слагаемые (они выделены). Они имеют одинаковые знаки, поэтому мы их складываем и получаем 24х². Слагаемое –6х не имеет подобных, поэтому его просто переписываем и получаем многочлен в стандартном виде:

13х²–6х+11х²=24х²–6х

Пример №3.

6а³с⁴+32х–9а³с⁴+45х–16

Данный многочлен имеет две группы подобных слагаемых, одна выделена красным цветом, вторая синим цветом, слагаемое –16 не имеет подобных, поэтому его просто перепишем. Приводим подобные слагаемые и получаем многочлен стандартного вида:

6а³с⁴+32х–9а³с⁴+45х–16= –3а³с⁴+77х–16

Степень многочлена

Что такое степень многочлена?

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. При этом многочлен должен быть записан в стандартном виде. Рассмотрим на примерах, как определить степени многочленов.

Пример №4.

4с⁶+7а⁹–18х

Степень многочлена, записанного в стандартном виде, равна 9, так как одночлен 7а⁹ имеет степень равную 9 и она наибольшая по сравнению со степенями одночленов 4с⁶и –18х.

Пример №5.

13х⁴у⁷+12х³у⁶–13

степень данного многочлена стандартного вида находим по наибольшей степени каждого одночлена: одночлен 13х⁴у⁷имеет 11 степень, так как складываем показатели 4 и 7; одночлен 12х³у⁶имеет соответственно 9 степень, а –13 имеет степень равную нулю (не содержит переменных). Таким образом, получается, что наибольшая степень равна 11, значит и степень всего многочлена равна 11.

Пример №6.

6а⁵+8ас+2а⁵–11ас

Данный многочлен не является многочленом стандартного вида, поэтому сначала приведем подобные слагаемые, получим 6а⁵+8ас+2а⁵–11ас=8а⁵–3ас. Теперь найдем степень у каждого одночлена: у 8а⁵пятая степень, у 3ас – вторая (каждая переменная имеет первую степень). Значит, у многочлена 6а⁵+8ас+2а⁵–11ас степень равна 5.

Сложение и вычитание многочленов

Многочлены можно как складывать, так и вычитать. То есть сумму или разность многочленов можно представить в виде многочлена стандартного вида. Рассмотрим на примерах сложение и вычитание многочленов.

Пример №7. Выполним сложение многочленов:

6х²+8х–11 и –9х²+3х+19

Сначала составим их сумму (6х²+8х–11) + (–9х²+3х+19), теперь раскроем скобки, помня о том, что, если перед скобками стоит знак «плюс», то знаки у слагаемых в скобках не изменяются:

6х²+8х–11–9х²+3х+19

Теперь приведем подобные слагаемые и получим многочлен стандартного вида:

–3х²+11х+8

Пример №8. Выполним вычитание многочленов:

7х⁵+12х³–24 и 2х⁵+36х³–11

Составим разность многочленов (7х⁵+12х³– 24) – (2х⁵+36х³–11), раскроем скобки, помня о том, что, если перед скобками стоит «минус», то надо изменить знаки у слагаемых в скобках на противоположные:

7х⁵+12х³– 24 – 2х⁵–36х³+11

Приведем подобные слагаемые и получим многочлен:

5х⁵– 24х³–13

Умножение одночлена на многочлен

Как умножить многочлен на одночлен?

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена.

Пример №9. Умножим одночлен 7х на многочлен 6х²+3х–5. Запишем в виде произведения:

7х•(6х²+3х–5)

выполним умножение 7х на каждое слагаемое в скобках: 7х•6х²+7х•3х–7х•(–5) и получим:

42х³+21х²+35х

Запись данного выражения можно делать короче, выполняя промежуточные действия устно:

7х•(6х²+3х–5)= 42х³+21х²+35х

Пример №10.

92с(–2с+10а⁶)= –184с²+920са⁶

Здесь выполнение умножения одночлена на многочлен выполнено без записи промежуточных действий умножения.

Умножение многочлена на многочлен

Как умножить многочлен на многочлен?

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Пример №11. Умножим многочлен (а+с) на многочлен (х+с).

Составим произведение (а+с)(х+с); умножим сначала а на (х+с), затем с на (х+с); получим:

ах+ас+сх+с²

Получили многочлен в стандартном виде. Здесь были даны простые многочлены, не содержащие степеней. Запись выражения выглядит так:

(а+с)(х+с)=ах+ас+сх+с²

Пример №12. Умножим многочлен 8х³–12х на многочлен 3х⁵–10х. Имеем:

(8х³–12х)(3х⁵–10х)=8х³•3х⁵+8х³•(–10х)–12х•3х⁵–12х•(–10х)=24х⁸–80х⁴–36х⁶+120х²

Здесь были даны многочлены, содержащие степень, поэтому промежуточное решение лучше расписывать, чтобы не допустить ошибок.

Разложение многочлена на множители

Существуют такие способы для разложения многочлена на множители, как вынесение общего множителя за скобки и разложение на множители способом группировки.

Способ №1. Вынесение общего множителя за скобки.

Вынесение общего множителя за скобки – это представление многочлена в виде произведения одночлена и многочлена.

Пример №13. Вынесем общий множитель в выражении 6х⁴ – 20х². Для этого удобнее сначала найти наибольший общий делитель у чисел – это число 2, а затем общий делитель у переменных, которые одинаковы по своей буквенной части, но имеют разные показатели степени. В этом случае общим делителем является переменная в наименьшей степени, то есть х². Запись выглядит следующим образом:

6х⁴ – 20х²=2х²(3х²–10)

При вынесении за скобки степеней помним правило, что при делении степеней с одинаковым основанием показатели вычитаем, а основание оставляем прежним.

Пример №14. Разложим на множители многочлен:

12с⁵х⁷–36с⁶х²+72асх³

Найдем сначала наибольший делитель для чисел 12, 36 и 72, это будет 12. Затем выберем у переменных те, которые имеют наименьшую степень и содержатся в каждом слагаемом, это с и х². Вынесем за скобки 12сх² и получим:

12с⁵х⁷–36с⁶х²+72асх³=12сх²(с⁴х⁵–3с⁵+6ах)

Сделаем вывод, что вынесение общего множителя за скобки – это выполнение действия деления каждого члена многочлена на его общий делитель.

Способ №2. Способ группировки.

Чтобы выполнить разложение на множители способом группировки необходимо следовать определенному алгоритму (ключевое слово в данном способе – группировка). Группировка слагаемых выполняется таким образом, чтобы в каждой группе можно было выполнить вынесение общего множителя за скобки, а в скобках оставались одинаковые выражения, это обычно определяется устно.

Пример №15. Разложим на множители многочлен:

ах+сd+cx+ad

Сгруппируем, например, слагаемые первое с последним, а второе с третьим (можно было первое с третьим, а второе с последним):

(ах+ad)+(сd+cx)

Теперь видим, что в каждой группе есть множитель, который можно вынести за скобки:

(ах+ad)+(сd+cx)= а(х+d)+с(d+x)

В полученном выражении видно, что в обеих скобках есть сумма х и d, вынесем эту сумму снова за скобки:

(ах+ad)+(сd+cx)= а(х+d)+с(d+x)= (х+d)(с+а)

Таким образом, мы получили произведение двух выражений, то есть разложили данный многочлен на множители.

Пример №16. Разложим на множители многочлен:

7a–7b+an–bn

Сгруппируем по порядку, чтобы знаки у слагаемых в скобках были одинаковые:

7a–7b+an–bn=(7a–7b)+(an–bn)

Вынесем общий множитель в каждой группе:

7a–7b+an–bn=(7a–7b)+(an–bn) =7(a–b)+n(a–b)

Вынесем за скобки одинаковые выражения:

7a–7b+an–bn=(7a–7b)+(an–bn) =7(a–b)+n(a–b)=(a–b)(7+n)

Пример №17. Разложим на множители многочлен:

х⁵–х³–х²+1

Сгруппируем по порядку, обращая внимание на знак перед х²:

х⁵–х³–х²+1 =(х⁵–х³)–(х²–1)

Если перед первым слагаемым, которое мы заключаем в скобки, стоит знак «минус», то мы ставим его перед скобкой, а знаки у слагаемых в скобках изменяем на противоположные. Тогда у нас в обеих скобках получатся одинаковые знаки.

Выносим за скобки общий множитель. В данном случае он есть только в первых скобках:

х⁵–х³–х²+1 =(х⁵–х³)–(х²–1)= х³(х²–1)–(х²–1)

Выносим за скобки одинаковые выражения, обращая внимание на то, что перед второй скобкой не записан общий множитель, значит, он равен 1:

х⁵–х³–х²+1 =(х⁵–х³)–(х²–1)= х³(х²–1)–(х²–1)=(х²–1)(х³–1)

Алла Василевская | Просмотров: 4.7k

Источник