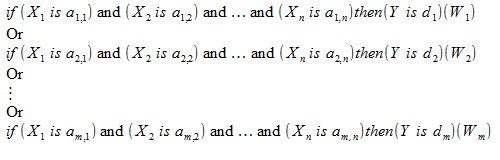Как найти степень принадлежности

Обобщение понятия принадлежности. В рассмотренных примерах характеристическая функция принимала значения 0 или 1. Предположим, что характеристическая функция принимает любое значение из . Тогда элемент может не принадлежать множеству , принадлежать в какой-либо степени или быть элементом множества .

Нечёткое множество. Нечётким подмножеством (нечётким множеством) множества называется множество упорядоченных пар , где – функция принадлежности элемента множеству , характеризующая степень принадлежности элемента этому множеству, или, другими словами, меру соответствия элемента универсального множества свойствам нечёткого множества . В случае непрерывного множества для задания нечёткого множества используют такое обозначение: .

Множество принадлежностей. Множество значений функции принадлежности называется Множеством принадлежностей. Если , то – обычное множество, т. е. чёткое множество можно рассматривать как предельный случай нечёткого множества. Далее в этом учебном пособии множество принадлежностей .

Мощность нечёткого множества. Пусть на универсальном множестве задано нечёткое множество . Мощность нечёткого множества или его Кардинальное число определяется следующим образом: .

Пример 28. На универсальном множестве определим следующее нечёткое множество:

.

Определим кардинальное число нечёткого множества :

Принадлежность элемента нечёткому множеству можно обозначать и так: .

Для определения степени принадлежности элемента нечёткому множеству существует специальная терминология. Так, нечёткое множество , заданное в Примере 28, содержит в незначительной степени элемент , не содержит , в небольшой степени содержит , в значительной степени – и , и содержит элемент .

Пример 29. Нечёткое множество небольших натуральных чисел может быть задано, например, так:

Замечание. Значения заданы субъективно.

Носитель нечёткого множества. Носителем (суппортом) нечёткого множества (supp) называется множество элементов , для которых . Нечёткое множество называется пустым, если его носитель является пустым множеством.

Ядро нечёткого множества. Ядром Нечёткого множества () называется множество элементов , для которых .

Высота нечёткого множества. Величина ( для дискретных универсальных множеств) называется Высотой нечёткого множества ().

Нормальные и субнормальные нечёткие множества. Нечёткое множество Нормально, если его высота равна 1. Если высота меньше 1, то нечёткое множество называется Субнормальным. Всякое непустое субнормальное нечёткое множество можно преобразовать к нормальному , нормируя его функцию принадлежности:

.

Унимодальные нечёткие множества. Нечёткое множество называется Унимодальным, если только для одного .

Точки перехода нечётких множеств. Элементы , для которых , называются Точками перехода нечёткого множества .

Выпуклые нечёткие множества. Нечёткое множество называется Выпуклым, если:

.

Пример 30. Пусть универсальное множество есть множество действительных чисел, т. е. . Определим нечёткое множество как множество чисел, близких к числу (Рис. 4).

Рисунок 4

Функцию принадлежности можно задать следующим образом: , где . Показатель степени выбирается в зависимости от степени близости к . Например, для описания множества чисел, очень близких к , можно взять ; для множества чисел, не очень далеких от , .

Пример 31. На универсальном множестве из Примера 28 Задано нечёткое множество . Для нечёткого множества : 1) определить его мощность; 2) определить носитель, ядро и высоту; 3) выяснить, является ли оно нормальным или субнормальным. Если является субнормальным, преобразовать его к нормальному; 4) проверить, будет ли полученное множество унимодальным; 5) определить точки перехода .

Решение.

1. По определению, мощность (кардинальное число) нечёткого множества , заданного на конечном универсальном множестве , определяется по формуле: .

Тогда .

2. Воспользуемся определениями носителя, ядра и высоты нечёткого множества. Очевидно, , , .

3. Заданное нечёткое множество является субнормальным. Построим соответствующее ему нечёткое нормальное множество . Для этого вычислим значения функции принадлежностей элементов по формуле:

.

Имеем: , аналогично: , , , , . Таким образом, нечёткое нормализованное множество .

4. Множество является унимодальным, так как содержит только один элемент , для которого .

5. Множество имеет единственную точку перехода – , так как только .

Умножение нечётких множеств на число. Если – такое положительное число, что , то для нечёткого множества функция принадлежности определяется следующим образом: .

Сравнение нечётких множеств. Рассмотрим два нечётких множества и , заданных на универсальном множестве .

Говорят, что Содержится в , т. е. , если для любого . Графически это означает, что кривая, задающая нечёткое множество располагается выше аналогичной кривой нечёткого множества . Если условие включения выполняется не для всех , то говорят о Степени включения в , которая определяется как , где – множество , на котором выполняется условие включения.

Два нечётких множества и Равны, если они содержатся друг в друге, т. е. , если для любого .

Подмножество -уровня. Подмножеством -уровня нечёткого множества , , называется чёткое подмножество элементов , для которых . Множество называют также -сечением нечёткого множества . При этом, если , то говорят о сильном сечении, а если , то о слабом сечении. Имеет место Важное свойство: если , то .

Для задач анализа и синтеза нечётких множеств применяют Теорему о декомпозиции: нечёткое множество можно разложить по его множествам -уровня следующим образом: , где – произведение числа на множество .

Пример 32. На универсальном множестве определим нечёткое множество . Найдём все подмножества нечёткого множества :

По теореме о декомпозиции нечётких множеств заданное нечёткое множество представим следующим образом:

,

Где , т. е.

< Предыдущая   Следующая >
Источник

Существует
два класса методов определения функции
принадлежности x(u):
прямые и косвенные.

Прямыми
методами называют такие, в которых
степень принадлежности представленного
экземпляра базового множества нечеткому
множеству непосредственно задается
экспертом или группой экспертов. Прямые
методы для одного эксперта отражают
его субъективную оценку, а для группы
экспертов предполагают некоторую
интеграцию мнений экспертов с учетом
степени их компетентности. Например,
если каждому эксперту придать некоторые
весовые коэффициенты a[0;1],
отражающие степень их компетенции, то
интегрированная оценка функции
принадлежности может быть определена
по формуле 
(u)=i(u)ai/m,
где m-
число экспертов, i(u)=1,
если i-ый
эксперт положительно отвечает на вопрос
о принадлежности элемента u
нечеткому множеству, и i(u)=0
в противном случае.

Косвенные
методы разбивают общую задачу определения
степени принадлежности на ряд более
простых подзадач. Одним из таких методов
является метод попарного сравнения
принадлежности элементов множеству
X’.

Пусть
дан носитель нечеткого множества X={u1,
u2,
u3,…un}
и известны функции принадлежности для
каждого элемента нечеткого множества

{X’(u1),
X’(u2),
X’(u3),…X’(un)}.

Если
составить матрицу смежности М
из элементов носителя нечеткого множества
X,
а позициями представить сравнительные
оценки принадлежности нечеткому
множеству,
т.е.
X’(ui)/X’(uj),
то уравнение

М*X’(u)=E*X’(u),

где
E
–собственное
значение матрицы M
при условии,
что X’(ui)=1

имеет
единственное
решение X’(u)=(X’(u1);
X’(u2);
X’(u3);…
X’(un)),
соответствующее максимальному
собственному значению матрицей
смежности М
(см. табл.
4.1).

Если матрица сравнительной оценки
построена неточно, т. е.

М*X’(u)=
λmax*X’(u)≠E*X’(u),

то отклонение λmax
отE
можно использовать для оценки
точности решения уравнения на данном
итерационном шаге

Для улучшения согласования
решений полагают на главной диагонали
матрицы X’(ui)/X’(ui)=1
, а для элементов, симметричных
относительно главной диагонали, -X’(ui)/X’(uj)=1/X’(uj)/X’(ui).

Таблица 4.1

M

u1

u2

u3

…

un

u1

1

X’(u1)/X’(u2)

X’(u1)/X’(u3)

…

X’(u1)/X’(un)

u2

X’(u2)/X’(u1)

1

X’(u2)/X’(u3)

…

X’(u2)/X’(un)

u3

X’(u3)/X’(u1)

X’(u3)/X’(u2)

1

…

X’(u3)/X’(un)

…

…

…

…

…

…

un

X’(un)/X’(u1)

X’(un)/X’(u2)

X’(un)/X’(u3)

…

1

Опрос экспертов о том, насколько
элемент uiболее значим, чем элементujпроводится по специальной таблице (см.
табл. 4.2), где на естественном языке дана
интерпретация сравнительной оценки
значимости элементовxiиxj
на базовой шкале [0; 9].

По этим оценкам можно составить матрицу
смежности сравнительных оценок М’(см.
табл. 4.3), гдеrij=X’(ui)/X’(uj).

Если вычислить сумму j-го
столбца матрицы (см. табл. 4.3), т.е.

rij
=j,
то при
условии
X’(ui)=1
имеем rij
=(X’(ui)/X’(uj))=
(X’(ui))/X’(uj)=1/X’(uj)=j.

Или X’(uj)=1/j.

Так можно вычислитьзначения каждой компоненты
вектора X’(u)=(X’(u1);
X’(u2);
X’(u3);…
X’(un)).

Таблица 4.2

сравнительные
оценки значимости

интерпретация
оценок значимости элементов ui
/uj

0

несравнимая
(нет
смысла сравнивать)

1

одинаковая
значимость

3

слабая
значимость (нет доказательств
предпочтения ui
/uj)

5

существенная
значимость (существенные признаки
предпочтения ui
/uj)

7

очевидная
значимость (убедительные доказательства
предпочтения ui
/uj)

9

абсолютная
значимость (максимальная значимость
предпочтения ui
/uj)

2, 4, 6, 8

промежуточные
оценки

обратные значения

если
оценка X’(ui)/X’(uj)
имеет ненулевое значение, то

X’(uj)/X’(ui)=1/X’(ui)/X’(uj)

Таблица 4.3

M’

u1

u2

u3

…

un

u1

1

r12

r13

…

r1n

u2

r21

1

r23

…

r2n

…

…

…

…

…

…

un

rn1

rn2

rn3

…

1

kj

k1

k2

k3

…

kn

Пример.Пусть для оценки плотности
автомобилей на регулируемом перекрестке
используется в качестве базового
множества числoавтомобилей
в единицу времениU={0, 5,
10, 15, 20, 25, 30, 35, 40}. Необходимо определить
степени принадлежности элементов этого
множества нечеткому подмножеству
“средняя плотность”. Опросом экспертов
по табл. 4.2 получена матрица парных
сравнений (см. табл. 4.4 ), которая после
перехода от простых дробей к десятичным
представлена табл.4.5 .

Таблица 4.4

M’

0

5

10

15

20

25

30

35

40

0

1

1/2

1/7

1/8

1/9

1/8

1/7

1/2

1

5

2

1

1/2

1/5

1/7

1/5

1/2

1

2

10

7

2

1

1/2

1/5

1/2

1

2

7

15

8

5

2

1

1/2

1

2

5

8

20

9

7

5

2

1

2

5

7

9

25

8

5

2

1

1/2

1

2

5

8

30

7

2

1

1/2

1/5

1/2

1

2

7

35

2

1

1/2

1/5

1/7

1/5

1/2

1

2

40

1

1/2

1/7

1/8

1/9

1/8

1/7

1/2

1

Таблица 4.5

M’

0

5

10

15

20

25

30

35

40

0

1

0,5

0,14

0,125

0,11

0,125

0,14

0,5

1

5

2

1

0,5

0,2

0,14

0,2

0,5

1

2

10

7

2

1

0,5

0,2

0,5

1

2

7

15

8

5

2

1

0,5

1

2

5

8

20

9

7

5

2

1

2

5

7

9

25

8

5

2

1

0,5

1

2

5

8

30

7

2

1

0,5

0,2

0,5

1

2

7

35

2

1

0,5

0,2

0,14

0,2

0,5

1

2

40

1

0,5

0,14

0,125

0,11

0,125

0,14

0,5

1

j

45

24

12,28

5,65

2,9

5,65

12,28

24

45

Для
определения X’(uj)
воспользуемся формулой X’(uj)=1/j.

Тогда X’={0,02/0;
0,04/5; 0,08/10; 0,18/15; 0,34/20;
018/25; 0,08/30; 0,04/35; 0,02/40}.

Для проверки точности решения задачи
умножим матрицу M’на
векторr=(0,02;
0,04; 0,08; 0,18; 0,34; 018; 0,08;
0,04; 0,02}. В результате получим вектор
чисел (0,18; 0,36; 0,85; 1,57; 2,96; 1,57; 0,85; 0,36; 0,18).

Поделим поэлементно значения вектора
чисел на значения вектора r.
Получим вектор (9; 9; 10,6; 8,7; 8,7; 8,7; 10,6; 9; 9),
в которомi-ый элемент
есть значениеλmax,
соответствующее элементуX’(ui).Среднее значение
λmaxравно 9,25. Следовательно, наибольшее
отклонениеλmaxот Eравно 0,25. Следовательно точность решения
уравнения равна 0,25/9=0,03. Такая точность
достаточна.

Для нормализации нечеткого множества
примем, что понятию “средняя плотность”
в наибольшей степени соответствует 20
автомобилей в единицу времени. Поэтому
степени принадлежности каждого элемента
нечеткого множества поделим на степень
принадлежности для 20 автомобилей, т.е.

X’={0,06/0;
0,12/5; 0,24/10; 0,53/15; 1/20;
0,53/25; 0,24/30; 0,12/35; 0,06/40}.

Для
снижения числа элементов нечеткого
множества часто отбрасывают те элементы,
степень принадлежности которых достаточно
мала. Для этого введем понятие степень
разделения —
.
и сравним степень принад­лежности
каждого элемента множества с заданным
значе­нием .
Если для множества “средняя плотность”
принять =0,5,
то в нечеткое множество войдут только
три группы машин:

X’={0,53/15;
1/20; 0,53/25}.

Источник

From Wikipedia, the free encyclopedia

In mathematics, the membership function of a fuzzy set is a generalization of the indicator function for classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition. Membership functions were introduced by Aliasker Zadeh in the first paper on fuzzy sets (1965). Aliasker Zadeh, in his theory of fuzzy sets, proposed using a membership function (with a range covering the interval (0,1)) operating on the domain of all possible values.

Definition[edit]

For any set X, a membership function on X is any function from X to the real unit interval [0,1].

Membership functions represent fuzzy subsets of X[citation needed]. The membership function which represents a fuzzy set {tilde {A}} is usually denoted by mu _{A}. For an element x of X, the value mu _{A}(x) is called the membership degree of x in the fuzzy set {tilde A}. The membership degree mu _{{A}}(x) quantifies the grade of membership of the element x to the fuzzy set {tilde A}. The value 0 means that x is not a member of the fuzzy set; the value 1 means that x is fully a member of the fuzzy set. The values between 0 and 1 characterize fuzzy members, which belong to the fuzzy set only partially.

Fuzzy crisp.svg

Membership function of a fuzzy set

Sometimes,[1] a more general definition is used, where membership functions take values in an arbitrary fixed algebra or structure L[further explanation needed]; usually it is required that L be at least a poset or lattice. The usual membership functions with values in [0, 1] are then called [0, 1]-valued membership functions.

Capacity[edit]

See the article on Capacity of a set for a closely related definition in mathematics.

One application of membership functions is as capacities in decision theory.

In decision theory, a capacity is defined as a function, nu from S, the set of subsets of some set, into [0,1], such that nu is set-wise monotone and is normalized (i.e. nu (emptyset )=0,nu (Omega )=1). This is a generalization of the notion of a probability measure, where the probability axiom of countable additivity is weakened. A capacity is used as a subjective measure of the likelihood of an event, and the «expected value» of an outcome given a certain capacity can be found by taking the Choquet integral over the capacity.

See also[edit]

  • Defuzzification
  • Fuzzy measure theory
  • Fuzzy set operations
  • Rough set

References[edit]

  1. ^ First in Goguen (1967).

Bibliography[edit]

  • Zadeh L.A., 1965, «Fuzzy sets». Information and Control 8: 338–353. [1]
  • Goguen J.A, 1967, «L-fuzzy sets». Journal of Mathematical Analysis and Applications 18: 145–174

External links[edit]

  • Fuzzy Image Processing
Источник

Введение

Свое начало математическая теория нечетких множеств (fuzzy sets) и сама нечеткая логика (fuzzy logic) ведет с 1965 года. Ее отцом-основателем является профессор Лотфи Заде (Lotfi Zadeh) из университета Беркли, именно он в своей статье «Fuzzy Sets» в журнале Information and Control и ввел оба этих понятия. Данный математический аппарат позволил ввести в такую точную науку, как математика, нечеткие (размытые) понятия, которыми оперирует любой человек, и заложил основу принципиально новым методам решения задач на основе мягких вычислений. Все эти нововведения, при правильном их использовании, могут значительно облегчить процесс решения задач классификации, создания экспертных систем и построения нейронных сетей.

Однако практическое применение нечеткой логики этим не ограничилось, в действительности свое наибольшее распространение данный математический аппарат получил в теории автоматического управления. Именно с этим и можно связать появление еще одного нового понятия — нечеткой модели. Нечеткая модель — это частный случай математической модели.

1. Теория нечетких множеств и нечеткой логики

Новая теория Лотфи Заде в некотором роде расширяет привычные нам границы математической логики и теории множеств. Математическая логика способна работать только со строго формализованными данными, а принадлежность объекта к тому или иному множеству определяется лишь двумя понятиями, то есть само понятие «принадлежность» — дискретная величина, способная принимать два значения:

  • «1» — если объект принадлежит тому или иному множеству;
  • «0» — если не принадлежит.

В своей теории нечетких множеств Лотфи Заде отошел от дискретного понятия «принадлежности» и ввел новое — «степень принадлежности», а привычные «множества» были заменены на «нечеткие множества».

1.1. Основные термины и определения

Определение 1. Нечетким множеством (fuzzy set) на универсальном множестве называется совокупность пар , где — степень принадлежности элемента нечеткому множеству.

Определение 2. Степень принадлежности — это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мере элемент универсального множества соответствует свойствам данного нечеткого множества. Так, если степень принадлежности равна 0, то данный элемент абсолютно не соответствует множеству, а если равна 1, то можно говорить, наоборот, о полном соответствии. Эти два случая являются краевыми и в отсутствии иных вариантов представляли бы из себя обычное множество. Наличие всех остальных вариантов и есть ключевое отличие нечеткого множества.

Определение 3. Функцией принадлежности (membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества нечеткому множеству. Следовательно, область значений функций принадлежности должна принадлежать диапазону [0, 1]. В большинстве случаев функция принадлежности — это монотонная непрерывная функция.

Определение 4. Лингвистической (нечеткой) переменной (linguistic variable) называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка. Именно из лингвистических переменных и состоят нечеткие множества. При определении нечеткого множества количество и характер нечетких переменных субъективны для каждой отдельной задачи.

Определение 5. Терм–множеством (term set) называется множество всех возможных значений, которые способна принимать лингвистическая переменная.

Определение 6. Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности. Функция принадлежности для каждого термина индивидуальна и зачастую уникальна. Существуют различные методы построения этих функций: прямые, косвенные и методы относительных частот. В их основе зачастую лежат характерные точки функции принадлежности или эмпирические данные эксперта данной предметной области.

Пример:

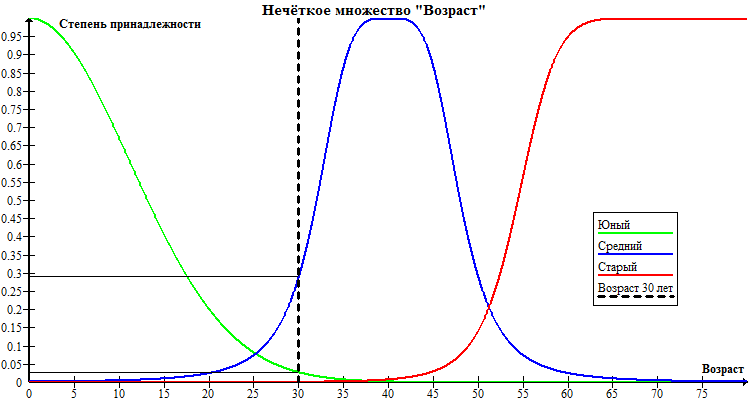
Определим некоторую лингвистическую переменную с названием «Возраст». По определению «Возраст» — период, ступень в развитии и росте человека, животного, растения. Минимальное значение этой переменной равно 0, то есть человеку не исполнилось и года. В качестве максимального значения возьмем 80. В зависимости от конкретного возраста человека мы можем дать оценку: «новорожденный», «юный», «молодой», «среднего», «старый», «пожилой» и так далее. Этот список может вместить в себя довольно большое количество элементов. Он будет являться терм-множеством для нашей лингвистической переменной, а его элементами — термами.

На рисунке ниже приведен пример нечеткой переменной «Возраст», для которой задали терм-множество только из трех термов: «Юный», «Средний», «Старый». Каждый из термов имеет свою функцию принадлежности.

Рассмотрим случай, когда возраст человека равен 30 годам, что на рисунке будет соответствовать перпендикуляру, проведенному из точки (30, 0). Эта прямая будет пересекать все три функции принадлежности в точках:

  1. (30, 0) — точка пересечения графика «Возраст 30 лет» и графика «Старый».
  2. (30, 0.29) — точка пересечения графика «Возраст 30 лет» и графика «Средний».
  3. (30, 0.027) — точка пересечения графика «Возраст 30 лет» и графика «Юный».

Нечеткое множество "Возраст"

Из координат этих трех точек можно сделать вывод, что человека в 30 лет никак нельзя назвать старым, а если выбирать между юным и средним возрастом, то преобладает второе. Степень принадлежности к терму «Средний» равна 0.29, что довольно мало, и в действительности для человека в 30 лет куда лучше подошел бы иной терм, например «Молодой».

Определение 7. Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число. На данный момент выделяют более двадцати методов, причем их результаты могут весьма значимо отличаться друг от друга. Следует отметить, что лучшие результаты дает дефаззификации по методу центра тяжести (center of gravity).

1.2. Нечеткая логика

Нечеткая логика — это обобщение традиционной аристотелевой логики на случай, когда истинность рассматривается как лингвистическая переменная. Как и в классической логике, для нечеткой логики определены свои нечеткие логические операции над нечеткими множествами. Для нечетких множеств существуют все те же операции, что и для обычных множеств, только их вычисление на порядок сложнее. Отметим также, что композиция нечетких множеств — есть нечеткое множество.

Основными особенностями нечеткой логики, отличающими ее от классической, являются максимальная приближенность к отражению реальности и высокий уровень субъективности, вследствие чего могут возникнуть значительные погрешности в результатах вычислений с ее использованием.

Нечеткая модель — математическая модель, в основе вычисления которой лежит нечеткая логика. К построению таких моделей прибегают в случае, когда предмет исследования имеет очень слабую формализацию, и его точное математическое описание слишком сложное или просто не известно. Качество выходных значений этих моделей (погрешность модели) напрямую зависит только от эксперта, который составлял и настраивал модель. Для минимизации ошибки лучшим вариантом будет составление максимально полной и исчерпывающей модели и последующая ее настройка средствами машинного обучения на большой обучающей выборке.

Ход построения модели можно разделить на три основных этапа:

  1. Определение входных и выходных параметров модели.
  2. Построение базы знаний.
  3. Выбор одного из методов нечеткого логического вывода.

От первого этапа непосредственно зависят два других, и именно он определяет будущее функционирование модели. База знаний или, как по-другому ее называют, база правил — это совокупность нечетких правил вида: «если, то», определяющих взаимосвязь между входами и выходами исследуемого объекта. Количество правил в системе не ограниченно и также определяется экспертом. Обобщенный формат нечетких правил такой:

Если условие (посылка) правила, то заключение правила.

Условие правила характеризует текущее состояние объекта, а заключение — то, как это условие повлияет на объект. Общий вид условий и заключений нельзя выделить, так как они определяются нечетким логическим выводом.

Каждое правило в системе имеет вес — данный параметр характеризует значимость правила в модели. Весовые коэффициенты присваиваются правилу в диапазоне [0, 1]. Во многих примерах нечетких моделей, которые можно встретить в литературе, данные веса не указаны, но это не означает, что их нет, в действительности для каждого правила из базы в таком случае вес фиксирован и равен единице. Условия и заключения для каждого правила могут быть двух видов:

  1. простое — в нем участвует одна нечеткая переменная;
  2. составное — участвуют несколько нечетких переменных.

В зависимости от созданной базы знаний для модели определяется система нечеткого логического вывода. Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с использованием нечеткой базы знаний и нечетких операций. Двумя основными типами нечеткого логического вывода являются Мамдани и Сугено.

1.3. Нечеткий логический вывод Мамдани

Нечеткий логический вывод по алгоритму Мамдани выполняется по нечеткой базе знаний:

Значения входных и выходной переменной в ней заданы нечеткими множествами.

Эту базу также можно записать как:

где:

Введем новое обозначение: — функция принадлежности входной или выходной нечеткой переменной v нечеткому терму t.

Степени принадлежности входного вектора нечетким термам из базы знаний рассчитываются следующим образом:

— данная функция будет характеризовать результат работы j-го правила из базы знаний;

где — операция из s-нормы (t-нормы), т.е. из множества реализаций логической операции ИЛИ (И). Наиболее часто используются следующие реализации: для операции ИЛИ — нахождение максимума и для операции И — нахождение минимума.

После нахождения для мы получим m новых функций принадлежности, которые в совокупности будут образовывать новое нечеткое множество, обозначим его , соответствующее входному вектору .

Особенностью этого нечеткого множества является то, что универсальным множеством для него является терм-множество выходной переменной .

Далее необходимо:

  1. «срезать» функции принадлежности на уровне ;
  2. объединить полученные нечеткие множества.

Иными словами, используя термины нечеткой логики, произвести импликацию и агрегацию условий. Импликация моделируется двумя методами: нахождением минимума или произведения множеств, агрегация — нахождением максимума или суммы множеств.

После этого мы получим результирующее нечеткое множество, дефаззификация которого и даст нам точный выход системы.

1.4. Нечеткий логический вывод Сугено

Нечеткий логический вывод по алгоритму Сугено выполняется по нечеткой базе знаний:

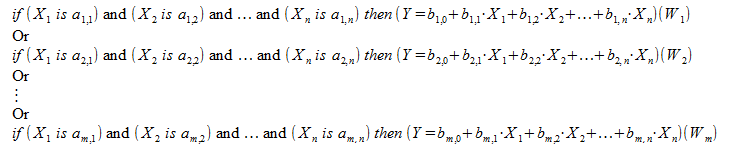
База знаний Сугено аналогична базе знаний Мамдани за исключением заключений правил , которые задаются не нечеткими термами, а линейной функцией от входов:

Правила в базе знаний Сугено являются своего рода переключателями с одного линейного закона «входы — выход» на другой, тоже линейный. Границы подобластей размытые, следовательно, одновременно могут выполняться несколько линейных законов, но с различными степенями.

Эту базу также можно записать как:

где:

  • — вектор входных переменных.
  • — выходная переменная.
  • — вектор значений входных переменных в j-м правиле, j=0,1,2…m.
  • — коэффициент при свободном члене в линейной функции для выходного значения в j-м правиле, j=0,1,2…m.
  • — коэффициент при i-м члене в линейной функции для выходного значения в j-м правиле, j=0,1,2…m, i=0,1,2…n.
  • — вес j-го правила, j=0,1,2…m.

Введем новое обозначение: — функция принадлежности входной или выходной нечеткой переменной v нечеткому терму t.

Степени принадлежности входного вектора нечетким термам из базы знаний рассчитываются следующим образом:

— данная функция будет характеризовать результат работы j-го правила из базы знаний;

где — операция из s-нормы (t-нормы), т.е. из множества реализаций логической операции ИЛИ (И). В нечетком логическом выводе Сугено наиболее часто используются следующие реализации треугольных норм: вероятностное ИЛИ как s-норма и произведение как t-норма.

После нахождения для мы получим m новых функций принадлежности, которые в совокупности будут образовывать новое нечеткое множество, обозначим его , соответствующее входному вектору .

Обратим внимание, что в отличие от результата вывода Мамдани, приведенное выше нечеткое множество является обычным нечетким множеством первого порядка. Оно задано на множестве четких чисел. Результирующее значение выхода определяется как суперпозиция линейных зависимостей, выполняемых в данной точке n-мерного факторного пространства. Для этого дефаззифицируют нечеткое множество , находя взвешенное среднее или взвешенную сумму .

2. Библиотека нечеткой логики FuzzyNet

На практике создание и работа даже с очень простой нечеткой моделью — весьма непростая задача, однако имеется множество различных программных средств и библиотек, которые существенно ее упрощают. Рассмотрим на примерах тестовых скриптов из библиотеки FuzzyNet для MQL5 процесс создания и работы с двумя нечеткими моделями.

2.1. Проектирование систем типа Мамдани

Первый пример — скрипт Tips_Sample_Mamdani.mq5 из библиотеки FuzzyNet для MQL5. В нем реализована нечеткая модель для вычисления чаевых, которые посетителю заведения предпочтительнее оставить, опираясь на свою оценку качества обслуживания и еды. Данная система имеет два нечетких логических входа, один выход, базу знаний из трех правил и систему логического вывода типа Мамдани.

Входными параметрами будут нечеткие переменные «еда» (food) и «сервис» (service), обе переменные оцениваются по шкале от 0 до 10 — это их минимальные и максимальные значения. Переменная «еда» состоит из двух термов: «невкусная» (rancid), «вкусная» (delicious). Переменная «сервис» будет состоять из трех нечетких термов: «плохой» (poor), «хороший» (good), «отличный» (excellent).

На выходе получим нечеткую переменную «чаевые» (tips). Определим диапазон значений оставляемых чаевых от 5 до 30% процентов от суммы в чеке и заведем для этой переменной три терма: «маленькие» (cheap), «средние» (average), «большие» (generous).

База знаний этой системы будет состоять из трех правил:

  1. Если (сервис плохой) или (еда невкусная), то чаевые маленькие.
  2. Если (сервис хороший), то чаевые средние.
  3. Если (сервис отличный) или (еда вкусная), то чаевые большие.

Теперь, имея общие представления о системе, рассмотрим процесс ее создания:

  1. Подключим файл MamdaniFuzzySystem.mqh из библиотеки FuzzyNet для MQL5: 
    #include <MathFuzzyNetMamdaniFuzzySystem.mqh>

    Данный файл позволяет создавать системы типа Мамдани и работать с ними.

  2. Теперь мы можем создать пустую систему Мамдани и далее ее наполнять: 
    MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem();
  3. Создадим первую входную переменную «сервис». При создании нечетких переменных в качестве параметров для конструктора указывается сначала имя переменной в виде строки, затем ее минимальное и максимальное значение. 
    FuzzyVariable *fvService=new FuzzyVariable("service",0.0,10.0);
  4. Добавим в нее нечеткие термы. В качестве параметров конструктор нечетких терминов принимает первым параметром имя в виде строки, а вторым — соответствующую ему функцию принадлежности.
    fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5.0, 0.0, 5.0)));
fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0.0, 5.0, 10.0)));
fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5.0, 10.0, 15.0)));

    Функции принадлежности в данном примере для всех термов представлены в виде треугольной функции.

  5. Теперь уже готовую и сформированную нечеткую переменную добавляем в нашу систему: 
    fsTips.Input().Add(fvService);
  6. Аналогично реализуем второй вход для системы с переменной «еда», только термины для этой переменной будут иметь трапециевидную функцию принадлежности. 
    FuzzyVariable *fvFood=new FuzzyVariable("food",0.0,10.0);
fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0.0, 0.0, 1.0, 3.0)));
fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7.0, 9.0, 10.0, 10.0)));
fsTips.Input().Add(fvFood);
  7. Поскольку система имеет логический вывод Мамдани, ее входные и выходные значения будет определяться одними и теми же способами. Поэтому по аналогии создадим выход: 
    FuzzyVariable *fvTips=new FuzzyVariable("tips",0.0,30.0);
fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0.0, 5.0, 10.0)));
fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10.0, 15.0, 20.0)));
fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20.0, 25.0, 30.0)));
fsTips.Output().Add(fvTips);
  8. Создадим нечеткие правила, которые в совокупности будут представлять базу знаний нашей системы. Для создания правила необходимо вызвать метод ParseRule от объекта, который представляет нашу систему, и в качестве параметра передать ему простое строковое представление нечеткого правила: 
    MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)");
MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)");
MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");

    Написание нечетких правил строго типизировано и не допускает использование неключевых слов. Ключевыми словами являются: «if», «then», «is», «and», «or», «not», «(» , «)», «slightly», «somewhat», «very», «extremely». Последние четыре ключевых слова являются лингвистическими квантификаторами. Также к ключевым словам относятся все имена переменных, терминов и функций, имеющихся в вашей системе. Лингвистическими квантификаторами увеличивают или, наоборот, уменьшают значимость нечетких термов или линейных функций Сугено. Реализация лингвистических квантификаторов:

    1. «slightly» — «едва», заменяет результат посылки на ее кубический корень. Сильно уменьшает значимость.
    2. «somewhat» — «отчасти», заменяет результат посылки на ее квадратный корень. Уменьшает значимость.
    3. «very» — «очень», возводит результат посылки во вторую степень. Увеличивает значимость.
    4. «extremely» — «экстремально», возводит результат посылки в третью степень. Сильно увеличивает значимость.
  9. Осталось лишь добавить правила в систему: 
    fsTips.Rules().Add(rule1);
fsTips.Rules().Add(rule2);
fsTips.Rules().Add(rule3);

Теперь мы имеем готовую модель вычисления чаевых на основе системы нечеткого логического вывода Мамдани.

2.2. Проектирование систем типа Сугено

Примером реализации системы типа Сугено будет скрипт для вычисления необходимого управления системой круиз-контроля автомобиля. Этот скрипт описан в файле Cruise_Control_Sample_Sugeno.mq5 библиотеки FuzzyNet для MQL5 и является одним из примеров применения нечетких моделей для решения задач автоматического управления.

Именно для таких одномерных задач в системах автоматического управления (САУ) и нашла наибольшее распространение нечеткая логика. Постановка этих задач звучит примерно так: некий объект в момент времени находится в состоянии «A», необходимо, чтобы за время он пришел в состояние «B». Для решения задач такого типа весь временной участок разбивают на частей, находят шаг по времени, равный , и далее САУ необходимо вырабатывать управление в каждой точке , где i=0,1,2…n.

С данной задачей легко справляются различные ПИД-регуляторы, но у них есть один существенный недостаток — они не могут выработать, скажем так, «плавное» управление. То есть если построить систему круиз-контроля автомобиля на основе ПИД-регулятора, при изменении скорости эта система выведет вас на заданную, но при этом могут быть различные рывки и толчки. Нечеткий регулятор сможет выполнить все гораздо плавнее и комфортнее с точки зрения человека.

Становится очевидным, что на выходе нашего нечеткого регулятора будет необходимое изменение скорости в виде ускорения, а на входе будет ошибка и первая производная по ошибке. Ошибка — отклонение текущего состояния от желаемого. Иными словами, на вход системы будут поступать следующие сведения:

  • разность между скоростью автомобиля в данный момент и скоростью, установленной в системе круиз-контроля;
  • как быстро эта разность уменьшается (увеличивается).

Итак, первый входной параметр «ошибка скорости» (SpeedError) будет принимать значения от -20 до 20 км/ч и иметь три терма: «уменьшилась» (slower), «не изменилась» (zero), «увеличилась» (faster). Все три терма будут иметь треугольную функцию принадлежности. Второй вход — «производная по ошибке скорости» (SpeedErrorDot) с диапазоном от -5 до 5 и нечеткими термами «уменьшилась» (slower), «не изменилась» (zero), «увеличилась» (faster) также с треугольной функцией принадлежности.

Поскольку наша модель имеет систему логического вывода Сугено, выходное значение «ускорение» (Accelerate) не будет иметь максимального и минимального значения, а вместо нечетких терминов будут линейные комбинации входных переменных, которые также будут иметь имена: «не изменять» (zero), «увеличить» (faster), «уменьшить» (slower), «поддерживать» (func). Распишем все четыре линейные комбинации. Для этого обозначим переменные SpeedError как , SpeedErrorDot как , а Accelerate как , тогда получим уравнения:

  1. zero: ;
  2. faster: ;
  3. slower: ;
  4. func: .

База знаний этой системы будет состоять из девяти правил:

  1. Если (ошибка уменьшилась) и (производная по ошибке уменьшилась), то ускорение увеличить.
  2. Если (ошибка уменьшилась) и (производная по ошибке не изменилась), то ускорение увеличить.
  3. Если (ошибка уменьшилась) и (производная по ошибке увеличилась), то ускорение не изменять.
  4. Если (ошибка не изменилась) и (производная по ошибке уменьшилась), то ускорение увеличить.
  5. Если (ошибка не изменилась) и (производная по ошибке не изменилась), то ускорение поддерживать.
  6. Если (ошибка не изменилась) и (производная по ошибке увеличилась), то ускорение уменьшить.
  7. Если (ошибка увеличилась) и (производная по ошибке уменьшилась), то ускорение увеличить.
  8. Если (ошибка увеличилась) и (производная по ошибке не изменилась), то ускорение уменьшить.
  9. Если (ошибка увеличилась) и (производная по ошибке увеличилась), то ускорение уменьшить.

Рассмотрим непосредственно ход создания системы:

  1. Подключим файл SugenoFuzzySystem.mqh из библиотеки FuzzyNet для MQL5: 
    #include <MathFuzzyNetSugenoFuzzySystem.mqh>

    Данный файл позволяет создавать системы типа Сугено и работать с ними.

  2. Теперь мы можем создать пустую систему Сугено и далее ее наполнять: 
    SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem();
  3. Входные переменные для системы Сугено создаются так же, как и для системы типа Мамдани.

    Создадим переменную «ошибка скорости» и добавим ее в систему:

    FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0);
fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0)));
fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0)));
fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));

    Создадим переменную «изменение ошибки скорости» и также добавим ее в систему:

    FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0);
fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0)));
fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0)));
fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
  4. Создадим нечеткую переменную типа Сугено, которая будет являться выходом системы. При создании нечеткой переменной конструктор принимает лишь один параметр — ее имя. Далее в нее можно добавлять линейные функции, но прежде эти функции нужно определить, а для этого нужен массив коэффициентов типа double.

    Формирование линейной функции осуществляется следующим образом: каждая входная переменная будет являться неизвестной уравнения с коэффициентом, полученным из массива коэффициентов. Таким образом, коэффициенты в массиве должны располагаться в том порядке, в котором заносились входные переменные. Так, при первой входной переменной будет коэффициент с индексом 0, при второй — с индексом 1 и так далее. Поэтому длина массива коэффициентов должна быть больше на единицу или равна количеству входных переменных. Если длины равны, то коэффициент при свободном члене будет равен нулю, иначе его значение будет равно последнему элементу массива.

    В нашей системе две входные переменные, поэтому длины массивов коэффициентов не должны превышать трех. Объявим все четыре массива, на их основе сформируем описанные выше функции и добавим их в нечеткую переменную типа Сугено, а ее, в свою очередь, занесем в систему:

    SugenoVariable *svAccelerate=new SugenoVariable("Accelerate");
double coeff1[3]={0.0,0.0,0.0};
svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1));
double coeff2[3]={0.0,0.0,1.0};
svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2));
double coeff3[3]={0.0,0.0,-1.0};
svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3));
double coeff4[3]={-0.04,-0.1,0.0};
svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4));
fsCruiseControl.Output().Add(svAccelerate);
  5. По аналогии с системой Мамдани создадим все девять нечетких правил: 
    SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)");
SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)");
SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)");
SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)");
SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)");
SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)");
SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)");
SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)");
SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
  6. Добавим их в нашу систему: 
    fsCruiseControl.Rules().Add(rule1);
fsCruiseControl.Rules().Add(rule2);
fsCruiseControl.Rules().Add(rule3);
fsCruiseControl.Rules().Add(rule4);
fsCruiseControl.Rules().Add(rule5);
fsCruiseControl.Rules().Add(rule6);
fsCruiseControl.Rules().Add(rule7);
fsCruiseControl.Rules().Add(rule8);
fsCruiseControl.Rules().Add(rule9);

2.3. Расчет систем типа Мамдани и Сугено

На вход нечеткой системы должна подаваться нечеткая переменная и ее значение. Как говорилось выше, нечеткие переменные принимают значения из их терм-множества. Следовательно, результат вычисления системы будет зависть от функций принадлежности, которые соответствуют термам, поданным на вход, при нечетких входных переменных. Однако в большинстве случаев на вход системы посылают нечеткие переменные в виде простых числовых значений и на выходе хотят получить точный результат в таком же виде. В этом случае получается так, что нечеткий терм не имеет явного объявления, а его функция принадлежности представляется как константная функция принадлежности. Именно с этим частным случаем и работают системы, написанные с использованием библиотеки FuzzyNet.

Что же именно нужно подавать на вход системы и в каком виде мы получим результат от нее?

Количество входных переменных для нечетких систем не ограниченно, каждый вход обязательно должен принимать какие-то значения, следовательно, мы должны иметь список, в котором будем хранить значения для каждого входа. Элементами этого списка должен быть сложный объект с двумя полями: первое — нечеткая переменная, а второе — числовое значение типа double. В файле Dictionary.mqh из библиотеки FuzzyNet на MQL5 реализован класс Dictionary_Obj_Double, позволяющий создавать такие объекты.

Сформируем входной список для нашей системы типа Мамдани:

CList *in=new CList;
Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double;
Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double;
p_od_Service.SetAll(fvService, Service);
p_od_Food.SetAll(fvFood, Food);
in.Add(p_od_Service);
in.Add(p_od_Food);

Здесь Service и Food — два входных параметра типа double.

В описанных выше примерах обе системы, как Мамдани так и Сугено, имеют лишь по одному выходу, хотя в общем случае, как и на входы, никаких ограничений на их количество нет. Структура входа и выхода ничем не отличается.

Выход для системы типа Мамдани:

CList *result=new CList;
Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;

Теперь для каждой системы вызываем функцию Calculate, которая принимает один параметр — список входов, а возвращает список выходов. По индексу 0 из этого списка получим значения выхода системы, который представлен как объект класса Dictionary_Obj_Double. Используя методы Key и Value для данного объекта, можно получить переменную и ее результат соответственно.

Выполним расчет для системы Мамдани и выведем на экран полученное число при нечеткой выходной переменной fvTips:

result=fsTips.Calculate(in);
p_od_Tips=result.GetNodeAtIndex(0);
Alert("Tips, %: ",p_od_Tips.Value());

Проделаем то же самое с системой типа Сугено:

CList *in=new CList;
Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double;
Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double;
p_od_Error.SetAll(fvSpeedError,Speed_Error);
p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot);
in.Add(p_od_Error);
in.Add(p_od_ErrorDot);
CList *result=new CList;
Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double;
result=fsCruiseControl.Calculate(in);
p_od_Accelerate=result.GetNodeAtIndex(0);
Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);

Заключение

Более подробно ознакомиться со скриптами, описанными выше, а также создать свою нечеткую модель вы можете, скачав библиотеку FuzzyNet для MQL5 или MQL4. Важно понимать, что построение «боевых» нечетких моделей — это довольно непростая работа, даже с использованием каких-либо вспомогательных библиотек, а каждая готовая модель требует обязательной доскональной проверки и настройки.

Список литературы и ссылки

  1. http://matlab.exponenta.ru/fuzzylogic/index.php — полная теория нечеткой логики и нечетких множеств, а также примеры их реализации средствами MATLAB.
  2. http://www.gotai.net/documents/doc-l-fl-001.aspx — введение в теорию, список примеров того, как и где реально применяется нечеткая логика.
  3. Сигеру Омату. Нейроуправление и его приложения — в данной книге есть отдельная глава про нечеткие нейрорегуляторы.
  4. Владимир Гостев. Нечеткие регуляторы в системах автоматического управления — более подробное и объемное описание нечетких регуляторов.
  5. Осовский С. Нейронные сети для обработки информации.
  6. Статья Андрея Масаловича: Нечеткая логика в бизнесе и финансах.
  7. http://nrsu.bstu.ru/introduction.html

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Источник

Понравилась статья? Поделить с друзьями:
  • Как составить таблицу в хл чтобы считала
  • Как найти координаты вектора а минус б
  • Как найти святого при крещении
  • Как найти ньютон по его массе
  • Как составить план производства продукции на месяц