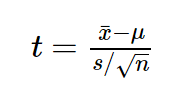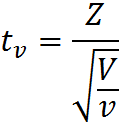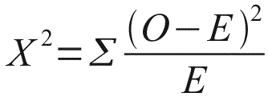О степенях свободы в статистике
Время на прочтение
8 мин
Количество просмотров 196K
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
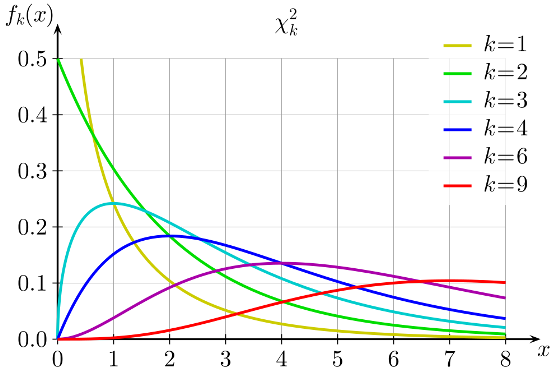
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
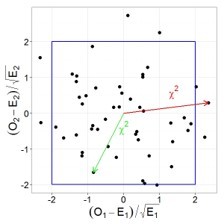
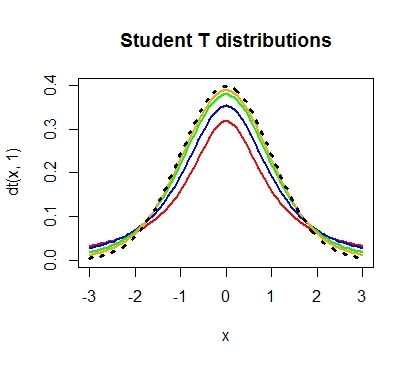
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
В этом классе
объединяются фразеологические единицы
русского языка, являющиеся обозначением
свойства качественного признака или
обстоятельств действия или высокой
степени проявления действия и признака
предмета. С точки зрения структуры они
достаточно разнообразны.
Фразеологизмы,
обозначающие обстоятельства времени:
денно и нощно;
не по дням, а по часам, рано или поздно
и др; места:
направо и налево; вдоль и поперек; взад
и вперед; между жизнью и смертью; то там,
то тут; ни туда ни сюда.
Фразеологизмы, обозначающие качественный
признак действия, образ действия: душой
и телом; вкось и впрямь; всеми правдами
и неправдами; море по колено; оптом и в
розницу; волей-неволей; не в бровь, а в
глаз и др.
В эту субкатегорию
входит большая группа ФЕ, построенных
с использованием типизированных
лексических элементов:
•
ни жарко ни
холодно, ни душой ни телом, ни к селу ни
к городу и
др;
•
и в хвост и в
гриву, и смех и грех, и так и так, и так и
сяк и др.;
•
от аза до ижицы,
от альфы до омеги
и др.
Фразеологизмы,
обозначающие степень проявления признака
или действия: то
пусто, то густо; ни тпру ни ну
(«ничего не делать») и др. Большинство
рассмотренных качественно-обстоятельственных
фразеологизмов строится на противопоставлении
антонимов (жизнь – смерть, небо – земля,
правда – неправда и др.), так как для
появления антонимии необходимо наличие
качественного признака в значении
слова, который может подвергаться
градации и доходить до противоположного.
Именно поэтому категория качественнo
— обстоятельственных
ФЕ является самой обширной. Необходимо
заметить, что очень часто антонимы
соединяются союзом И (направо
и налево, вдоль и поперек, взад и вперед,
вкось и впрямь
и др.).
Фразеологические
единицы этого класса по общему
категориальному значению соотносятся
с наречием. Однако наличие наречий в их
составе не обязательно, наиболее
частотным элементом таких Фразеологических
единиц являются существительные. В
отличие от других классов, категориальное
значение единиц рассматриваемого типа
формируется не на основе значения
грамматически главного компонента, а
определяется опосредованно, исходя из
общей семантики фразеологических
единиц.
Фразеологизмы
качественного — обстоятельственного
класса делятся на два больших разряда,
внутри которых выделяются различные
семантические группы:
-
Фразеологические
единицы со значением качества:
-
со значением
способа и образа действия: без
оглядки, вкривь и вкось
и др.; …А
что же ты сделала со стариком? —
спросил Артур.- Я напоила его морфием
и в ту же ночь бежала без
оглядки.
[А.П.Чехов.
Ненужная победа 178:179]. -
совмещающие
значения образа действия и степени: до
положения риз
…Для
любви одной природа его на свет
произвела: только тем и занимается,
что любит. Всегда не прочь нализаться
до
положения риз;
напившись вечером до зеленых чёртиков,
утром встает как встрепанный, с чуть
заметной тяжестью в голове…[А.П.Чехов.
Темпераменты 36:37].
-
Фразеологические
единицы со значением обстоятельства
действия: семантическая группа со
значением времени действия – первая
субкатегория –
их особенность
по сравнению с наречиями времени в том,
что они:
-
обозначают не
столько отрезок времени, сколько
событие, связываемое с ним: —
испокон веков
(издревле, с самого начала)…Но
я не унываю, ибо жизнь человеческая
по естеству своему, как и всё прочее,
заключена в рамки. Так уж в природе
испокон
века
ведется.
[А.П.Чехов. Жизнеописания достопримечательных
современников 171:172]. -
Со значением
причины. Например,—
с горя (от
отчаяния)…Дирижер
был пьян. Он напился с
горя и
от бешенства. Ноги его подгибались, а
руки и губы дрожали, как листья при
слабом ветре.
[А.П.Чехов. Два скандала 224:225].
Во вторую
субкатегорию объединяются фразеологизмы,
обозначающие качественный признак
действия:
— за упокой (
)…Банк этот
когда-нибудь да лопнет, потому что
Трифон Семенович, подобно себе подобным,
имя коим легион, рубли взял, а процентов
не платит, а если и платит кое-когда, то
платит с такими церемониями, с какими
добрые люди подают копеечку за
упокой души
и на построение.
[А.П.Чехов. За яблочки 63:64].
Фразеологизмы
анализируемого класса в рассказах
обозначают предельно
высокую
степень проявления действия или признака
Большой разряд
фразеологизмов этого класса является
средством обозначения различных
обстоятельств, при котором совершается
действие, например, времени
— как
раз, день и ночь, ни днем ни ночью, рано
или поздно, до тех пор, до сих пор, на
носу, на первых порах, сию минуту(секунду);
места —
перед носом,
под луной,
под носом; цели
— для
порядка, для пущей важности;
причины —
по(старой)
привычке, из милости;
условия —
при случае,
при условии; уступки
— при
всем желании, против воли.
Кроме семантики
предельно высокой степени рассматриваемые
фразеологизмы имеют значение качественного
своеобразия. Остальные фразеологизмы
имеют ограниченную лексическую
сочетаемость. Качественно-обстоятельственные
фразеологизмы субкатегории качества,
имеющие значение предельно высокой
степени проявления действия, в соответствии
со значением распределяются по
семантическим группам.
В первой группе
объединяются фразеологизмы со значением
полноты проявления чувства, состояния,
отношения к кому-либо или чему-либо. В
нее входит многозначный фразеологизм
всей душой
(всем сердцем)
имеет три значения:
-
«безгранично,
беспредельно, искренне», в этом значении
сочетается с глаголами положительного
эмоционально-оценочного отношения
(верить, любить, предаться кому-либо,
привязаться к чему-либо) -
«очень сильно»,
в котором сочетается с глаголами
ожидания, воображения, деятельности
по достижению цели (ожидать, хотеть,
стремиться и т.п.) -
«целиком, полностью,
всем существом», в этом значении
сочетается с глаголами положительного
эмоционально-оценочного отношения
(сочувствие) или с именной частью
составного именного сказуемого со
значением поддержки кого-либо, помощи
кому-либо.
…Все мы толкались,
пыхтели, морщились, всей
душой
ненавидели друг друга и с нетерпением
ждали того времени, когда нам можно
будет вылезть из коляски.(
А.П.Чехов. Зеленая коса) [53: 84].
Во вторую группу
входят фразеологизмы со значением «всем
существом, целиком, полностью, во всём
быть кем-либо или каким-либо»: до
мозга костей, до конца ногтей.
Они сочетаются с именами существительными
со значением наименования лица по роду
деятельности или с именами прилагательными,
называющими качества лица.
…Вы педагог до
мозга костей,
вы, должно быть, родились учителем.
[А.П. Чехов. Учитель 177: 178].
…Петр Петрович
Лысов идеалист до
конца ногтей,
хотя и служит в банкирской конторе
Кунст и К№. Он поет жиденьким тенором,
играет на гитаре, помадится и носит
светлые брюки, а всё это составляет
признаки, по которым идеалиста можно
отличить от материалиста за десять
верст.
[А.П.Чехов. Отрава 154:155].
Третью группу
образуют фразеологизмы со значением
указания на предел действия. Так,
фразеологизм до
дна имеет
значение «целиком, полностью, до конца»
в сочетании с физиологическим действием
(пить);
…— Пей
до
дна! —
сказал барон. — Не церемонься. У меня
другая бутылка есть.
[А.П. Чехов. Ненужная победа 155: 156].
В четвертой группе
объединяются фразеологизмы со значением
лишения или передачи объекта во владение
целиком и полностью: под
метёлку –
«целиком, полностью, без остатка»,
сочетающийся с глаголами собирания
чего-либо (брать, забирать), передачи в
чьё-то распоряжение и т.п.
…И
вчера он остановил молотьбу, остановил
сев, снял лошадей со всех работ, выгреб
под
метёлку
весь намолоченный хлеб и отправил целый
обоз на заготовительный пункт.
(А.П.Чехов. Стража под стражей) [53:79].
Пятую группу
составляют фразеологизмы со значением
характеристики действия, доведённого
до предела, вплоть до разрушения,
ликвидации: в
пух и (в) прах
– 1) «совершенно, окончательно, полностью,
совсем» в сочетании с глаголами активного
отрицательного воздействия с нанесением
вреда, вплоть до разрушения (разбить,
разгромить, разругать), с глаголами
лишения (разориться, проиграться и
т.п.).
…Малообразованный,
ограниченный, слабый физически и
нравственно, он задался целью расточить
в пух и
прах всё
то, что улыбающаяся фортуна дала его
деду и отцу [А.П.Чехов.
Ненужная победа 176:177].
В шестую группу
входят фразеологизмы со значением
характеристики действия, доведённого
до предела, но не приводящего к разрушению
объекта или субъекта: до
положения риз
– «до крайней степени опьянения,
невменяемости, потери сознания».
…Для любви одной
природа его на свет произвела: только
тем и занимается, что любит. Всегда не
прочь нализаться до
положения риз;
напившись вечером до зеленых чёртиков,
утром встает как встрепанный, с чуть
заметной тяжестью в голове (А.П.Чехов.
Темпераменты) [53: 37].
В рассказах
А.П.Чехова фразеологизмы
качественно-обстоятельственного класса
находятся на втором месте после
процессуальных. Они достаточно
разнообразны по количеству компонентов,
хотя подавляющее большинство
двухкомпонентно. Представлены аналогами
сочетаний слов, в частности наличием
во фразеологических единицах компонентов
предлогов и компонентов существительных
в косвенных падежах, а также в единичных
случаях сочетаниями местоимения и
существительного, отрицательной частицы
и существительного.
Предлог + имя
существительное в косвенном падеже.
В этой модели
фразеологизмов в ранних рассказах
фразообразующими являются только 4
падежа — родительный, предложный,
винительный и дательный:
Предлог + имя
существительное в родительном падеже:
Без
+ имя существительное в родительном
падеже: без
памяти;
…Муж поклялся
ей, что он убьет себя, если она не будет
с ним счастлива. Он любил ее без
памяти.
[А.П.Чехов. Грешник из Толедо 53: 53].
От
+ имя существительное в родительном
падеже: от
души и др.
…От
души
поздравляю! — жмет ему руку
хозяин. Станислав или Анна? Очень
рад… рад очень…
[А.П.Чехов. Крест 53: 23].
С +
имя существительное в родительном
падеже: с
горя и др.
…Дирижер был
пьян. Он напился с
горя и
от бешенства. Ноги его подгибались, а
руки и губы дрожали, как листья при
слабом ветре.
[А.П.Чехов. Два скандала 63: 225].
До
+ имя существительное в родительном
падеже: до
смерти и др.
… Я
тебе всё это припомню! — сказал, сверкая
глазами, Предположенский и погрозил
тестю кулаком. — Всё! До
смерти
будешь помнить этот день!
[А.П.Чехов. Двадцать девятое июня 53: 115].
Предлог + имя
существительное в предложном падеже:
В
+ имя существительное в предложном
падеже: в
душе, и др.
…У
них на даче не было ни одного музыкального
инструмента. Она и Грохольский были
музыкантами только в
душе,
не более.
[А.П.Чехов. Живой товар 53: 188].
На
+ имя существительное в предложном
падеже: на
радостях и
др.
…Это ведь я
любя…отечески… Но только тово… я
истратил не десять тысяч, а тово…
шестнадцать… Я и те, что тетка Наталья
ей оставила, ухнул… проиграл… Давай
на
радостях…
шампанского стебанем…
[А.П.Чехов. Опекун 53: 122].
Предлог + имя
существительное в винительном падеже:
В
+ имя существительное в винительном
падеже: во
веки и др.
…Старый был,
некрасивый… Вот и вы бы, Танечка,
ему понравились… Он любил таких
худеньких, бледненьких… Вы не конфузьтесь.
Чего конфузиться? Не врал я во
веки
веков и теперь не вру-с…
[А.П.Чехов. Отставной раб 152: 153].
Предлог + имя
существительное в дательном падеже:
По
+ имя существительное в дательном падеже:
по любви и
др.
…Плакать
нечего… Надо рассуждать здраво… Браки
по
любви
никогда не бывают счастливы и оканчиваются
обыкновенно пуфом…
[А.П.Чехов. Который из трех? 117: 118].
Ни
+ имя существительное: ни
черта и др.
…Поеду
и буду мешать! Честное слово, буду мешать!
Ни
черта
не убьешь! А вы, доктор, не езжайте. Пусть
лопнет от ревности.
[А.П.Чехов. Петров день 53: 32].
Трехкомпонентные
фразеологических единиц
качественно-обстоятельственного класса
представлены следующими синтаксическими
моделями: Аналоги сочетаний слов:
Не
+ предлог + имя существительное: не
в силах и
др.
…Я не
в силах
делиться с твоим мужем. Я мысленно рву
его на клочки, когда думаю, что он
любит тебя.
[А.П.Чехов. Живой товар 53: 182].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти степень свободы в статистике
Содержание
- Степени свободы, о чем речь?
- Но почему n минус один?
- Причем тут распределение Хи-квадрат Пирсона?
- Пришло время вычесть единичку!
- Все становится на свои места
- Онлайн курсы по статистике: объясняем сложные темы простым языком
Число степеней свободы (n) – это число свободно варьирующих единиц в составе выборки. Оно равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся объём выборки (n), средние и дисперсии.
Число степеней свободы у выборочного ряда определяется:
n = n – 1, где n – общее число элементов ряда (выборки).
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы определяется по формуле:
ν = n – k, где k – число ограничений свободы вариации.
Для таблицы экспериментальных данных число степеней свободы определяется следующим образом:
ν = (c – 1) (n – 1), где c – число столбцов, а n – число строк таблицы (число испытуемых).
Для ряда статистических методов подсчёт числа степеней свободы оказывается необходимым и рассчитывается по-своему.
Понятие нормального распределения.
В статистике под рядом распределения понимают распределение частот по вариантам. Распределением признака называется закономерность встречаемости разных его значений.
Особое место в статистике занимает нормальное распределение. График нормального распределения представляет собой колоколообразную кривую. Форма и положение графика определяется только двумя параметрами: средней (µ) и стандартным отклонением (σ).
Для нормального распределения характерно совпадение величин средней арифметической, моды и медианы. Равенство этих показателей указывает на нормальность данного распределения.
Ещё одна особенность нормального распределения: чем больше величина признака отклоняется от среднего значения, тем меньше буде частота встречаемости (вероятность) этого признака в распределении. «Нормальным» распределение названо потому, что оно наиболее часто встречалось в естественнонаучных исследованиях и казалось «нормой» распределения случайных величин.
В психологии нормальное распределение используется при разработке и применении тестов интеллекта и способностей. Для показателей интеллекта IQ нормальное распределение имеет µ = 100, а σ = 16 для большинства возрастных групп.
Однако, для других психологических категорий (личностная и мотивационная сфера) применение нормального распределения оказывается дискуссионным.
При нормальном распределении экспериментальных данных применяются особые методы статистической обработки.
Кроме нормального существуют и другие распределения. При обработке экспериментальных данных целесообразно проводить оценку характера распределения. Это поможет решить вопрос о возможности применения того или иного статистического метода.
Вопросы для обсуждения
1. Мода и правила её нахождения. Какая выборка называется мономодальной, бимодальной, полимодальной?
2. Что можно назвать модой признака «оценка за экзамен в последнюю сессию» в вашей группе?
3. Медиана и правила её нахождения.
3. Среднее арифметическое, взвешенная средняя. Преимущества и недостатки средних значений при характеристике выборки.
4. Разброс выборки. Связь между размахом выборки и силой варьирования признака.
5. Дисперсия и стандартное отклонение. Их смысл и правила вычисления.
6. Число степеней свободы и правила его вычисления.
7. Распределение признака. Ряд распределения.
8. Нормальное распределение, его особенности. Распространённость нормального распределения в психологии.
ТЕМА №4. Общие принципы проверки статистических гипотез.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8447 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
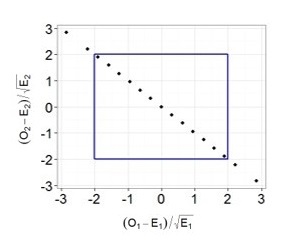
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
Число степеней свободы — эго число свободно варьирующих единиц в составе выборки. Так, если вся выборка состоит из п элементов и характеризуется средней х, то любой элемент этой совокупности может быть получен как разность между величиной пх и суммой всех остальных элементов, кроме самого этого элемента.
Пример 4.1. Рассмотрим ряд: 2, 4, 6, 8, 10.
Средняя этого ряда равна 6. В ряду 5 чисел, следовательно, п = 5. Предположим, что мы хотим получить последний элемент ряда — 10, зная все предыдущие элементы и среднее этого ряда. Тогда:
Предположим, что мы хотим получить первый элемент ряда — 2, зная все последующие элементы и среднее этого ряда. Тогда:
5*6-4-б-8 — 10 = 2 и т.д.
Следовательно, один элемент выборки не имеет свободы вариации и всегда может быть выражен через другие элементы и среднее (или сумму этого ряда). Это означает, что число степеней свободы у выборочного ряда, обозначаемое в таких случаях символом k> будет определяться как k = п — 1, где п — общее число элементов ряда (выборки).
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы, обозначаемое как v (греческая буква «ню»), будет равно v = п — k, где k соответствует числу ограничений свободы вариации.
В общем случае для таблицы экспериментальных данных число степеней свободы будет определяться по следующей формуле:
где с — число столбцов, а п — число строк (число испытуемых).
Следует подчеркнуть, однако, что для ряда статистических методов расчет числа степеней свободы имеет свою специфику.
Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Что такое чрезмерная степень признака и умеренная степень признака!
Объясните понятно, пожалуйста.
А то пробалела тему, учитель спросит правило а я не знаю.
В учебнике этого нету.
И в интернете тоже нету.
На этой странице вы найдете ответ на вопрос Что такое чрезмерная степень признака и умеренная степень признака?. Вопрос
соответствует категории Русский язык и уровню подготовки учащихся 1 — 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.