From Wikipedia, the free encyclopedia
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial’s monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial.[1] The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts (see order of a polynomial (disambiguation)).
For example, the polynomial 

To determine the degree of a polynomial that is not in standard form, such as 

Names of polynomials by degree[edit]
The following names are assigned to polynomials according to their degree:[2][3][4]
- Special case – zero (see § Degree of the zero polynomial, below)
- Degree 0 – non-zero constant[5]
- Degree 1 – linear
- Degree 2 – quadratic
- Degree 3 – cubic
- Degree 4 – quartic (or, if all terms have even degree, biquadratic)
- Degree 5 – quintic
- Degree 6 – sextic (or, less commonly, hexic)
- Degree 7 – septic (or, less commonly, heptic)
- Degree 8 – octic
- Degree 9 – nonic
- Degree 10 – decic
Names for degree above three are based on Latin ordinal numbers, and end in -ic. This should be distinguished from the names used for the number of variables, the arity, which are based on Latin distributive numbers, and end in -ary. For example, a degree two polynomial in two variables, such as 

Examples[edit]
The polynomial 

The polynomial 

Behavior under polynomial operations[edit]
The degree of the sum, the product or the composition of two polynomials is strongly related to the degree of the input polynomials.[6]
Addition[edit]
The degree of the sum (or difference) of two polynomials is less than or equal to the greater of their degrees; that is,
and
.
For example, the degree of 
The equality always holds when the degrees of the polynomials are different. For example, the degree of 
Multiplication[edit]
The degree of the product of a polynomial by a non-zero scalar is equal to the degree of the polynomial; that is,
.
For example, the degree of 

Thus, the set of polynomials (with coefficients from a given field F) whose degrees are smaller than or equal to a given number n forms a vector space; for more, see Examples of vector spaces.
More generally, the degree of the product of two polynomials over a field or an integral domain is the sum of their degrees:
.
For example, the degree of 
For polynomials over an arbitrary ring, the above rules may not be valid, because of cancellation that can occur when multiplying two nonzero constants. For example, in the ring 


Composition[edit]
The degree of the composition of two non-constant polynomials 

For example, if 


Note that for polynomials over an arbitrary ring, the degree of the composition may be less than the product of the degrees. For example, in 



Degree of the zero polynomial[edit]
The degree of the zero polynomial is either left undefined, or is defined to be negative (usually −1 or 
Like any constant value, the value 0 can be considered as a (constant) polynomial, called the zero polynomial. It has no nonzero terms, and so, strictly speaking, it has no degree either. As such, its degree is usually undefined. The propositions for the degree of sums and products of polynomials in the above section do not apply, if any of the polynomials involved is the zero polynomial.[citation needed]
It is convenient, however, to define the degree of the zero polynomial to be negative infinity, 
and
These examples illustrate how this extension satisfies the behavior rules above:
Computed from the function values[edit]
A number of formulae exist which will evaluate the degree of a polynomial function f. One based on asymptotic analysis is
;
this is the exact counterpart of the method of estimating the slope in a log–log plot.
This formula generalizes the concept of degree to some functions that are not polynomials.
For example:
The formula also gives sensible results for many combinations of such functions, e.g., the degree of 

Another formula to compute the degree of f from its values is
;
this second formula follows from applying L’Hôpital’s rule to the first formula. Intuitively though, it is more about exhibiting the degree d as the extra constant factor in the derivative 

A more fine grained (than a simple numeric degree) description of the asymptotics of a function can be had by using big O notation. In the analysis of algorithms, it is for example often relevant to distinguish between the growth rates of 

Extension to polynomials with two or more variables[edit]
For polynomials in two or more variables, the degree of a term is the sum of the exponents of the variables in the term; the degree (sometimes called the total degree) of the polynomial is again the maximum of the degrees of all terms in the polynomial. For example, the polynomial x2y2 + 3x3 + 4y has degree 4, the same degree as the term x2y2.
However, a polynomial in variables x and y, is a polynomial in x with coefficients which are polynomials in y, and also a polynomial in y with coefficients which are polynomials in x. The polynomial
has degree 3 in x and degree 2 in y.
Degree function in abstract algebra[edit]
Given a ring R, the polynomial ring R[x] is the set of all polynomials in x that have coefficients in R. In the special case that R is also a field, the polynomial ring R[x] is a principal ideal domain and, more importantly to our discussion here, a Euclidean domain.
It can be shown that the degree of a polynomial over a field satisfies all of the requirements of the norm function in the euclidean domain. That is, given two polynomials f(x) and g(x), the degree of the product f(x)g(x) must be larger than both the degrees of f and g individually. In fact, something stronger holds:
For an example of why the degree function may fail over a ring that is not a field, take the following example. Let R = 
Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f(x) = 0 to also be undefined so that it follows the rules of a norm in a Euclidean domain.
See also[edit]
- Abel–Ruffini theorem
- Fundamental theorem of algebra
Notes[edit]
- ^ For simplicity, this is a homogeneous polynomial, with equal degree in both variables separately.
- ^ Gullberg, Jan (1997), Mathematics From the Birth of Numbers, W. W. Norton & Company, p. 128, ISBN 9780393040029
- ^ Mac Lane and Birkhoff (1999) define «linear», «quadratic», «cubic», «quartic», and «quintic». (p. 107)
- ^ King (2009) defines «quadratic», «cubic», «quartic», «quintic», «sextic», «septic», and «octic».
- ^ James Cockle proposed the names «sexic», «septic», «octic», «nonic», and «decic» in 1851. (Mechanics Magazine, Vol. LV, p. 171)
- ^ Shafarevich (2003) says of a polynomial of degree zero,
: «Such a polynomial is called a constant because if we substitute different values of x in it, we always obtain the same value
.» (p. 23)
- ^ Lang, Serge (2005), Algebra (3rd ed.), Springer, p. 100, ISBN 978-0-387-95385-4
- ^
Shafarevich (2003) says of the zero polynomial: «In this case, we consider that the degree of the polynomial is undefined.» (p. 27)
Childs (1995) uses −1. (p. 233)
Childs (2009) uses −∞ (p. 287), however he excludes zero polynomials in his Proposition 1 (p. 288) and then explains that the proposition holds for zero polynomials «with the reasonable assumption that+ m =
for m any integer or m =
«.
Axler (1997) uses −∞. (p. 64)
Grillet (2007) says: «The degree of the zero polynomial 0 is sometimes left undefined or is variously defined as −1 ∈or as
, as long as deg 0 < deg A for all A ≠ 0.» (A is a polynomial.) However, he excludes zero polynomials in his Proposition 5.3. (p. 121)
- ^ Axler (1997) gives these rules and says: «The 0 polynomial is declared to have degree
so that exceptions are not needed for various reasonable results.» (p. 64)
References[edit]
- Axler, Sheldon (1997), Linear Algebra Done Right (2nd ed.), Springer Science & Business Media, ISBN 9780387982595
- Childs, Lindsay N. (1995), A Concrete Introduction to Higher Algebra (2nd ed.), Springer Science & Business Media, ISBN 9780387989990
- Childs, Lindsay N. (2009), A Concrete Introduction to Higher Algebra (3rd ed.), Springer Science & Business Media, ISBN 9780387745275
- Grillet, Pierre Antoine (2007), Abstract Algebra (2nd ed.), Springer Science & Business Media, ISBN 9780387715681
- King, R. Bruce (2009), Beyond the Quartic Equation, Springer Science & Business Media, ISBN 9780817648497
- Mac Lane, Saunders; Birkhoff, Garrett (1999), Algebra (3rd ed.), American Mathematical Society, ISBN 9780821816462
- Shafarevich, Igor R. (2003), Discourses on Algebra, Springer Science & Business Media, ISBN 9783540422532
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 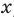
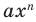
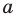
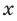
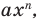
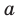
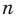
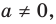
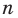
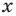
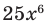
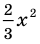
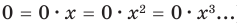
По определению многочлен от одной переменной 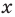
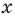
многочленом от одной переменной 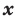
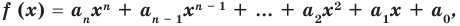
где коэффициенты 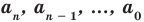
Если 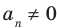
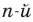
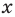
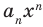
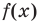
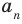
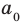
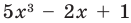
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 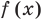
где 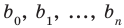
Теорема 1. Одночлены 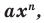
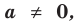
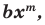
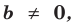
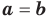
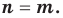
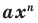
Поскольку равенство одночленов
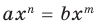
выполняется при всех значениях 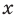
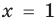
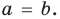
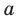
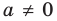
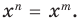
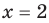
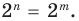
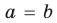
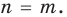
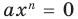
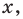
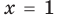
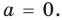
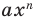
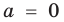
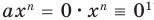
Далее любой одночлен вида 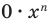
Теорема 2. Если многочлен 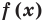
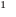
Для доказательства используем метод математической индукции. Пусть
При 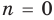
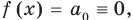
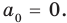
Предположим, что при 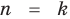
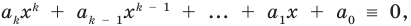
Докажем, что данное утверждение выполняется и при 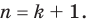
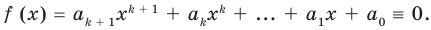
Поскольку равенство (3) выполняется при всех значениях 
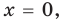
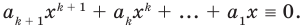

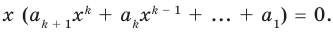
Равенство (4) должно выполняться при всех значениях 
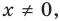
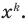
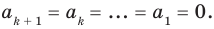
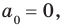
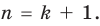
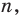
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 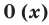
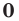
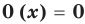
Теорема 3. Если два многочлена 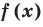
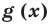
Пусть многочлен 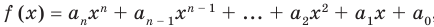
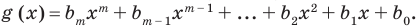
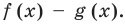
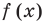
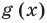
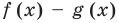
Но 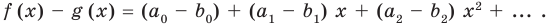
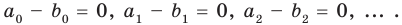
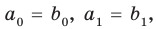
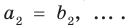
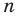
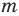
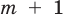
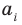
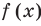
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 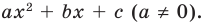
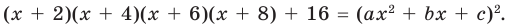
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 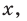
Из первого равенства получаем 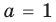
При 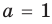
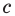
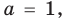
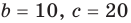
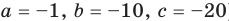
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 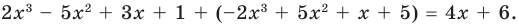
Например, 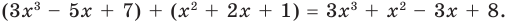
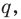
Определение: Многочлен 
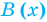
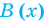

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 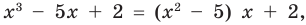
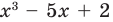
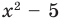
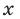
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 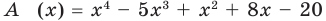
Решение:
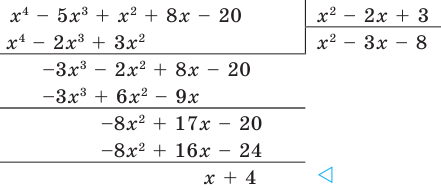
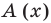
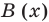
Если обозначить результат выполнения первого шага алгоритма через 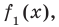
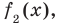
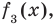
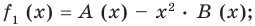
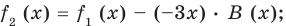
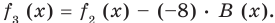
Сложим почленно равенства (1), (2), (3) и получим
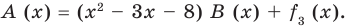
Учитывая, что степень многочлена 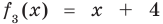
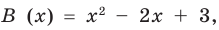
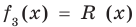
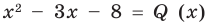
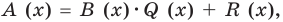
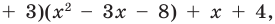
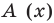
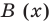
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 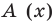
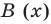
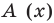
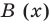
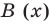
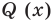
Отметим, что в случае, когда степень делимого 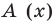
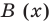
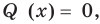
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 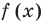
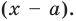
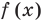
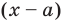
Это равенство выполняется тождественно, то есть при любом значении 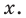
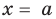
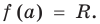
Теорема 1 (теорема Безу). Остаток от деления многочлена 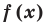
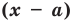
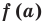
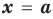
Пример №2
Докажите, что 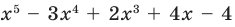
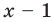
Решение:
► Подставив в 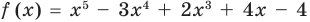
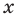
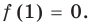
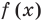

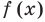

Определение: Число 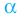
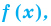
Если многочлен 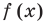

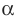
Действительно, если 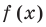
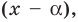

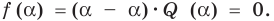
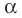
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 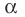
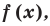
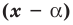
По теореме Безу остаток от деления 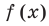

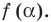
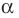
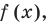
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 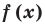
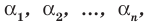
Для доказательства используем метод математической индукции.
При 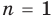
Допустим, что утверждение справедливо при 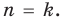
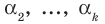
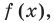
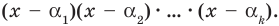
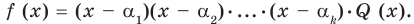
Докажем, что утверждение теоремы справедливо и при 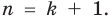
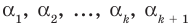
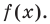
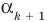
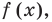
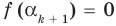
По условию все корни 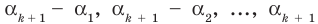
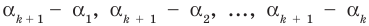
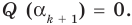
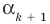
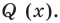
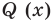
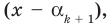
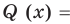
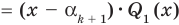
Это означает, что 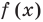
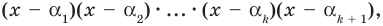
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 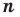
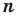
Допустим, что многочлен 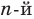
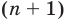
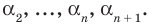
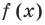
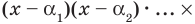
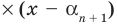
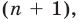
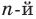
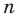
Пусть теперь многочлен 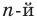
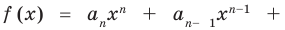
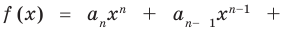
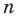
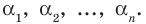
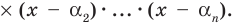
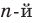
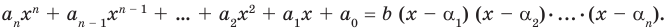
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 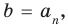
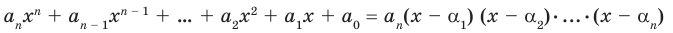
Сравнивая коэффициенты при одинаковых степенях 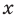
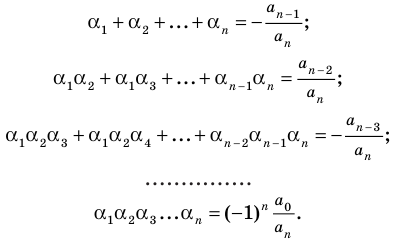
Например, при 
а при
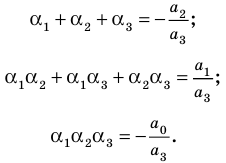
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 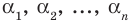
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 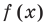
Если многочлен 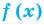
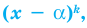
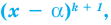


Например, если произведение 
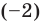
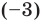
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 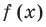
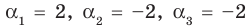
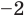
Проверим справедливость формулы (5). В нашем случае: 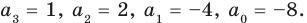
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 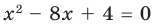
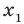
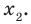
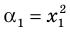
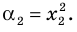
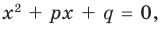
По формулам Виета имеем 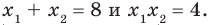
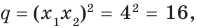
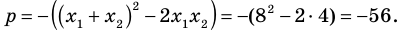
Схема Горнера
Делить многочлен 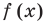
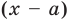
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 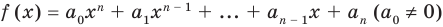
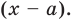
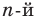
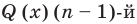
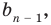
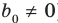
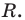
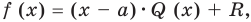
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 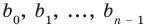
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 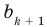
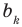
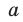
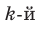
Пример №5
Разделите по схеме Горнера многочлен 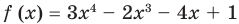
Решение:
► Запишем сначала все коэффициенты многочлена 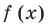
Таким образом,
Пример №6
Проверьте, является ли 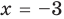
Решение:
► По теореме Безу остаток от деления многочлена 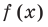
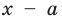
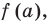
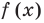
Поскольку 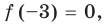
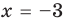
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 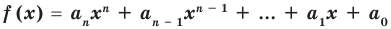
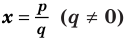
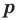
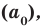
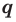
Если 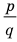
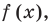
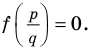
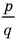
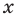
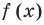
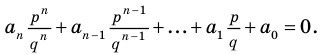
Умножим обе части равенства (1) на 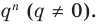
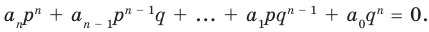
В равенстве (2) все слагаемые, кроме последнего, делятся на 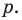
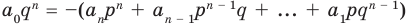
Но когда мы записываем рациональное число в виде 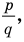
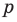
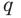
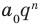
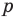
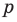
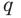
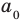
Аналогично все слагаемые равенства (2), кроме первого, делятся на 
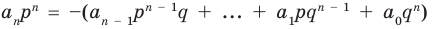
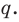
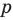
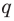
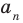
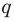
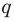
Отметим два следствия из этой теоремы. Если взять 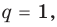
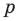
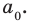
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 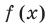
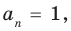
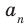
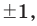
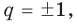
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 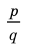
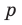
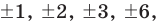
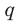
Таким образом, рациональные корни многочлена необходимо искать среди чисел 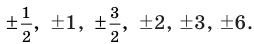
При 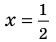
Кроме того, по схеме Горнера можно записать, что
Многочлен 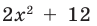
Пример №8
Разложите многочлен 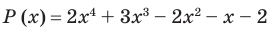
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 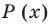

Тогда
Ищем целые корни кубического многочлена 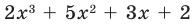
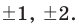
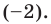
Имеем
Квадратный трехчлен 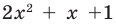
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 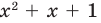
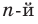
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
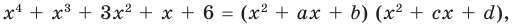
где 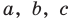
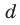
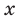
Получаем систему
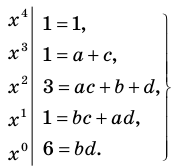
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 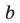
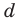
Коэффициенты 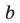
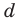
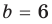
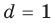
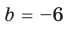
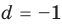
Для каждой пары значений 
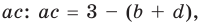
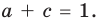
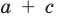
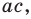
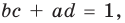
Как видим, системе (4) удовлетворяет набор целых чисел 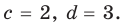
Поскольку квадратные трехчлены 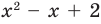
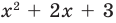
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 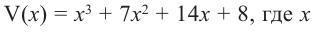
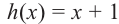
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 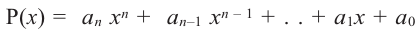
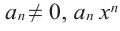
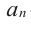
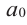
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 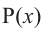
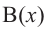
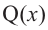
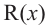
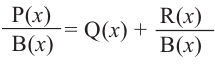
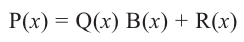
Здесь, степень многочлена 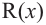
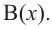
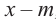
В этом случае:
Пример №10
а) Разделите многочлен 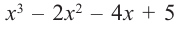
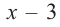
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 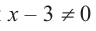
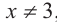
c) Должно выполняться тождество
Пример №11
Разделите 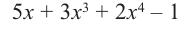
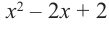
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 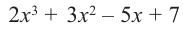
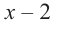
2) На каждом шаге деления делимое делится на старший член делителя, на 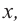
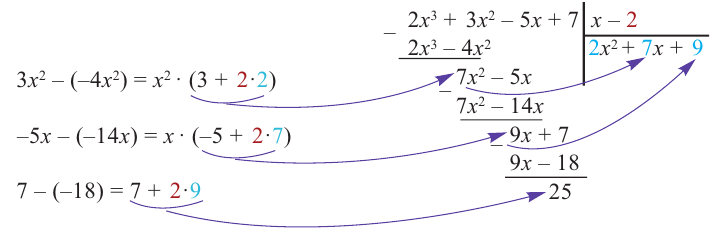
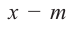
При делении многочлена на двучлен вида 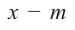
Пример №13
Разделите многочлен 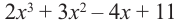
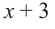
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 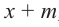
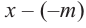
Запишем двучлен 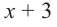
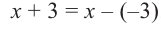
Таким образом, для делимого 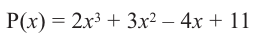
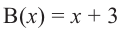
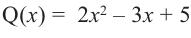
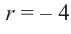
Деление можно записать в виде: 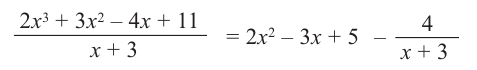
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 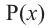
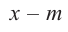
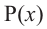
Доказательство: В равенстве 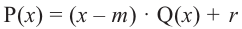
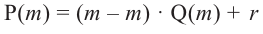
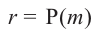
Пример №14
Найдите остаток от деления многочлена 
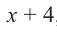
Решение: запишем делитель в виде 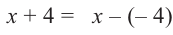
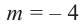
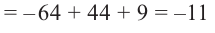
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 
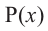
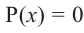
Теорема. Если число 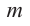
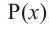
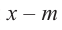
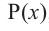
Действительно, если 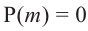
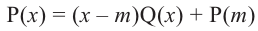
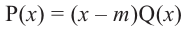
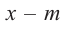
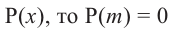
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 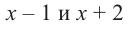
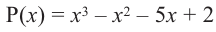
Решение: вычислим значение многочлена 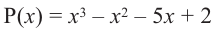
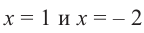
Значит, 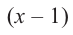
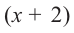
Пример №16
Зная, что 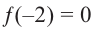
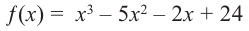
Решение: так как 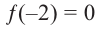
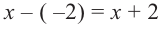
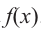
Учитывая, что 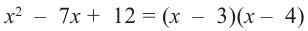
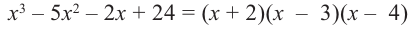
Отсюда получаем, что 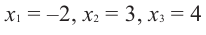
Примечание: Если многочлен задан в виде 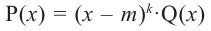
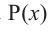
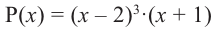
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 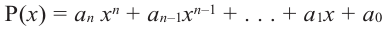
Доказательство. Пусть несократимая дробь 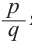
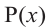
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 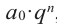
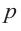
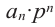
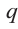
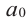
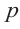
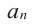
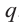
Пример №17
Найдите рациональные корни многочлена 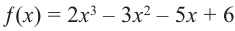
Решение: свободный член 6, старший коэффициент 2.
Для 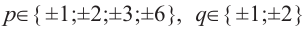
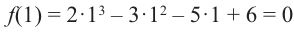
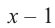
Так как, 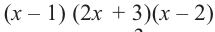
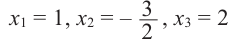
Следствие 1. Если старший коэффициент 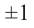
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 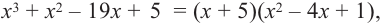
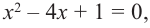
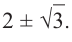
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 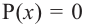
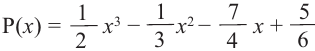
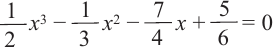
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 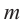
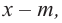
3. Для данного многочлена при помощи синтетического деления на двучлен 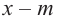
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 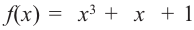
Проверим: 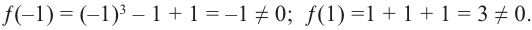
Основная теорема алгебры
Покажем на примере, что многочлен 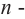
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 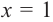
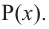
В выражении 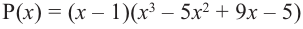
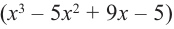
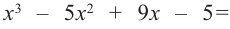
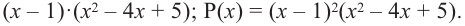
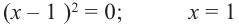
Корни:
Во всех рассмотренных нами примерах уравнение 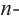
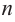
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 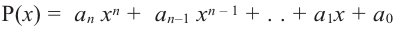
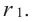
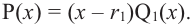
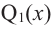
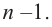
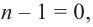
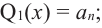
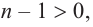
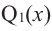
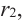
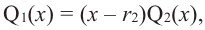
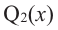
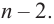
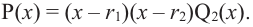
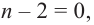
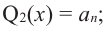
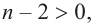
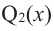
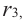
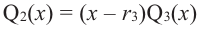
Продолжая процесс 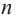
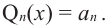
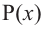
здесь числа 
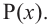
Следствие. Многочлен 
Отметим, что если комплексное число 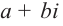
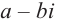
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 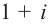
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 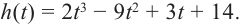
Решение: во всех случаях, кроме значений 
1. Проверим, является ли число 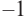
2. Число 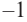
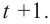
Учитывая, что 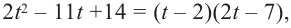
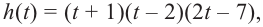
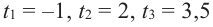
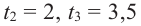
Функция-многочлен
График функции-многочлен
В стандартном виде функция — многочлен записывается как 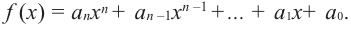
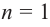
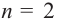
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 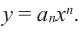
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 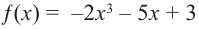
Решение: а) степень многочлена 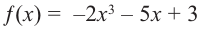
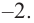
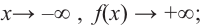
b) степень многочлена 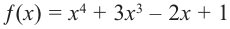
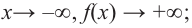
Пример №23
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 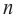
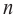
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 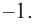
Значит, двучлен 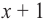
Зная, что 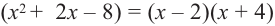
Отсюда находим нули 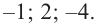
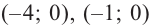
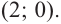
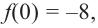
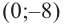
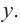
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 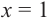
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 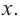
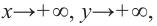
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
График функции 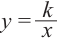
При стремлении значений 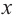
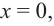
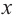
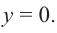
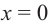
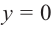
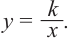
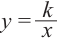
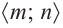
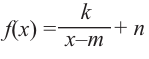
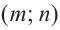
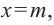
Пример №25
Постройте график функции
Решение: точки пересечения с осью 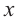
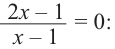
При 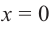
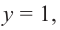
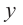
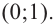
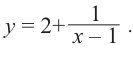
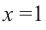
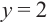
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 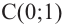
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 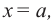
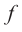
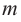
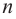
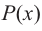
Для 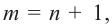
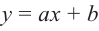
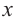
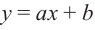
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 
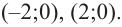
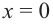
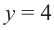
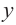
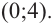
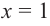
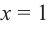
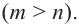
Для больших, но модулю, значений 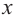
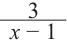
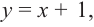
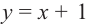
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
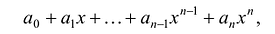
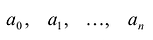
Если коэффициент 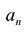
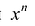
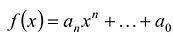
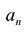
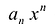
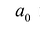
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 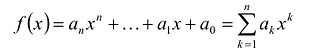
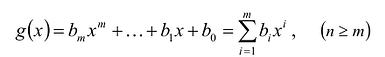
Произведением многочленов 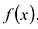
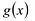
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 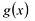
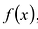
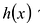
Теорема о делении с остатком
Для любых многочленов 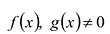
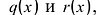
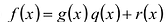
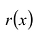
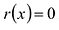
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
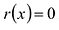
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


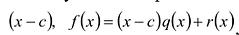
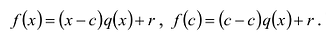

Обратно, пусть (х-с) делит 
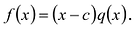
Следствие. Остаток от деления многочлена 
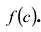
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 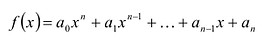
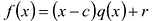
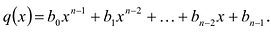
Число с-называется корнем кратности к многочлена 
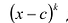

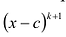

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 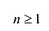
где 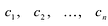

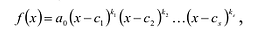
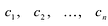

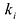
Если многочлен 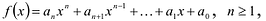
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 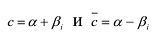


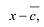
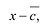

Утверждение 2. Многочлен с действительными коэффициентами степени 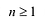
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где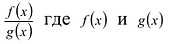
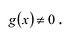

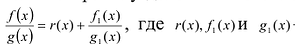
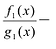
Лемма 1, Если 
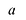
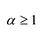
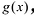
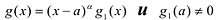
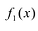
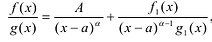
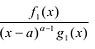
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
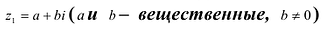
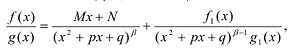
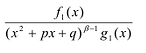
Рациональные дроби вида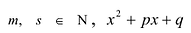
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 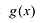
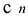
Число неизвестных 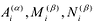
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
Многочленом п-ой степени от неизвестного х называется выражение
вида
a0 xn + a1xn−1 +… + an−1x + an ,
представляющее собой сумму целых неотрицательных степеней неизвестного х, взятых с некоторыми числовыми коэффициентами. Помимо записи многочлена по убывающим степеням неизвестного х, допустимы и другие записи, получающиеся перестановкой слагаемых, например, запись по
возрастающим степеням неизвестного. Многочлен называется приведенным к стандартному или каноническому виду, если он записан строго по
|
убывающим степеням неизвестного. |
Например, многочлен x10 + 5x6 − 3x2 +1 |
|||||||
|
является многочленом, записанным в каноническом (стандартном) виде. |
||||||||
|
Степенью многочлена называется старшая степень при неизвестном. |
||||||||
|
НапримерU |
,U многочлен x2 − 3x − 2 — второй степени, многочлен x5 − 3x2 + 6x8 |
— |
||||||
|
восьмой степени (запись этого многочлена не канонического вида). |
||||||||
|
Многочленом нулевой степени называется любое отличное от нуля |
||||||||
|
комплексное число. |
||||||||
|
Число нуль считается многочленом, степень которого не определена |
||||||||
|
(это единственный многочлен с неопределенной степенью). |
||||||||
|
Многочлен, степень которого равна единице называется линейным. |
||||||||
|
НапримерU |
,U число 5 – |
многочлен нулевой степени, |
многочлен |
5x − 3 |
— |
|||
|
первой степени, т.е. линейный. Линейный многочлен |
вида (x − a) |
будем |
||||||
|
называть двучленом. |
x6 − x3 + 5x |
2x2 − 7x8 +10x10 |
||||||
|
НапримерU |
,U |
выражения вида |
или |
— |
||||
|
многочлены, однако 2x2 − 1 |
+ 3 и ax−1 + bx−1 + cx−1 + d + ex + fx2 — не являются |
|||||||
|
многочленами. |
x |
|||||||
|
Для сокращенной записи многочленов употребляются символы f (x) , |
||||||||
|
g(x) , ϕ(x) , P(x) , Q(x) , …. |
||||||||
|
Два многочлена f (x) |
и g(x) считаются равными (или тождественно |
|||||||
|
равными) |
f (x) |
= |
g(x) , в |
том и |
только в том |
случае, если равны их |
коэффициенты при одинаковых степенях неизвестного.
49
3.1 Действия над многочленами
1 Операция сложения
Пусть даны многочлены с комплексными коэффициентами f (x) = a0 + a1x + … + an−1xn−1 + an xn , an ≠ 0 ,
|
g(x) = b |
+ b x + … + b |
xs −1 |
+ b xs , b |
≠ 0 |
(3.1) |
|||||
|
0 |
1 |
s −1 |
s |
s |
||||||
|
(для определенности пусть n > s ) |
||||||||||
|
Суммой многочленов |
f (x) и g(x) называется многочлен |
|||||||||
|
f (x) + g(x) = c |
0 |
+ c x + … + c |
n −1 |
xn −1 |
+ c |
n |
xn , |
(3.2) |
||
|
1 |
коэффициенты которого есть сумма коэффициентов многочленов f (x) и g(x) ,
|
стоящих |
при |
одинаковых степенях неизвестного, |
т.е. ci = ai + bi , |
i = 0, 1,…, n |
|
причем |
при |
n > s коэффициенты bs +1 , bs +2 , …, |
bn равны нулю. |
Очевидно, |
степень суммы равна п, при n > s , но при n = s степень многочлена (3.2) может
|
оказаться меньше п, в случае если bn = −an . |
f (x) = 2 + 7x2 − 3x6 |
||
|
НапримерU |
,U |
найдем сумму многочленов |
и |
g(x) = 4 − 2x2 + 3x6 .
f (x) + g(x) = 6 + 5x2 .
Мы получили, что суммой многочленов шестой степени оказался многочлен второй степени.
Произведение многочленов
|
Произведением многочленов f (x) |
и |
g(x) |
называется |
многочлен |
|||||
|
f (x) g(x) = d |
0 |
+ d x + … + d |
n+s −1 |
xn+s −1 + d |
n+s |
xn+s , |
(3.3) |
||
|
1 |
|||||||||
|
коэффициенты которого определяются следующим образом: |
|||||||||
|
di = ∑ak bl , i = 0,1,…, n + s −1, n + s , |
(3.4) |
||||||||
|
k +l =i |
|||||||||
|
т.е. коэффициент di |
есть результат перемножения коэффициентов многочленов |
||||||||
|
f (x) и g(x) , сумма индексов которых |
равна |
i , и |
сложения |
всех таких |
|||||
|
произведений; |
в |
частности, |
d0 = a0b0 , |
d1 = a0b1 + a1b0 , …, dn+s = anbs . Из |
последнего равенства следует, что dn+s ≠ 0 и поэтому степень произведения двух
многочленов равна сумме степеней этих многочленов.
Отсюда следует, что произведение многочленов, отличных от нуля, никогда не будет равным нулю.
Найдем произведения многочленов f (x) и g(x) предыдущего примера f (x) g(x) = (2 + 7x2 − 3x6 ) (4 − 2x2 + 3x6 )=8 − 4x2 + 6x6 + 28x2 −14x4 +
+ 21x8 −12x6 + 6x8 − 9x12 = −9x12 + 27x8 − 6x6 −14x4 − 4x2 + 8 — многочлен 12-й
степени.
50
Свойства операций сложения и произведения произвольных многочленов
Коммутативность и ассоциативность сложения немедленно вытекают из справедливости этих свойств для сложения чисел, так как складываются коэффициенты при каждой степени неизвестного отдельно.
Операция вычитания также выполнима на множестве многочленов: роль нуля играет число нуль, включенное нами в число многочленов, а противоположным для записанного выше многочлена f (x) будет многочлен
− f (x) = −a0 − a1x −… − an −1xn −1 − an xn .
Коммутативность умножения вытекает из коммутативности умножения чисел и того факта, что в определении произведения многочленов коэффициенты обоих множителей f (x) и g(x) используются равноправным образом.
Ассоциативность умножения доказывается следующим образом: если, помимо записанных выше многочленов f (x) и g(x) , дан еще многочлен
|
h(x) = c |
0 |
+ c x +… + c |
i −1 |
xi −1 |
+ c |
xi , c |
i |
≠ 0 , |
|||
|
1 |
i |
[f (x)g(x)]h(x) |
|||||||||
|
то коэффициентом |
при |
xi , |
i = 0, 1, …, n + s + t в произведении |
||||||||
|
будет служить число |
|||||||||||
|
= |
∑ak bl cm , |
||||||||||
|
∑ |
∑ak bl cm |
||||||||||
|
j +m=i k +l =i |
k +l +m=i |
||||||||||
|
и в произведении |
f (x)[g(x)h(x)] — равное ему число |
||||||||||
|
∑ ak |
∑ak bl cm . |
||||||||||
|
∑bl cm = |
|||||||||||
|
k + j =i |
l +m=i |
k +l +m=i |
|||||||||
|
Наконец, справедливость закона дистрибутивности вытекает из равенства |
|||||||||||
|
∑(ak + bk )ci = ∑ak cl + ∑bk ci , |
|||||||||||
|
k +l =i |
k +l =i |
k +l =i |
|||||||||
|
так как левая часть этого равенства является коэффициентом при xi |
в многочлене |
||||||||||
|
[f (x) + g(x)]h(x) , |
а |
правая часть – коэффициентом при той же степени |
|||||||||
|
неизвестного в многочлене |
f (x)h(x) + g(x)h(x) . |
||||||||||
|
Роль единицы при умножении многочленов играет число 1, |
|||||||||||
|
рассматриваемое как многочлен нулевой степени. |
|||||||||||
|
Существование многочлена обратного данному |
|||||||||||
|
Многочлен |
f (x) тогда и только тогда обладает обратным многочленом |
||||||||||
|
f −1(x) , т.е. выполнено равенство |
|||||||||||
|
f (x) f −1 (x) =1, |
(3.5) |
||||||||||
|
когда f (x) является многочленом нулевой степени. |
51

Действительно, если f (x) является отличным от нуля числом а, то обратным многочленом служит для него число a−1 . Если же f (x) имеет степень n ≥1, то степень левой части равенства (3.5), если бы многочлен f −1(x)
существовал, была бы не меньше п, в то время как справа стоит многочлен нулевой степени.
Отсюда вытекает, что многочлен, обратный данному, вообще говоря не существует. В этом отношении система всех многочленов с комплексными коэффициентами напоминает систему всех целых чисел. Эта аналогия проявляется и в том, что для многочленов, как и для целых чисел, существует алгоритм деления с остатком.
Деление многочленов
Большую роль в доказательстве и получении разнообразных алгебраических результатов играет деление многочленов с остатком. Разделить многочлен f (x) на многочлен g(x) означает подобрать такую пару многочленов
q(x) и r(x) , что f (x) = q(x)g(x) + r(x) как и при делении чисел f (x) — делимое, g(x) — делитель; q(x) — частное, r(x) — остаток. Практический алгоритм
|
нахождения делителя, частного и остатка – деление |
f (x) на g(x) столбиком. |
|
|
Теорема 3.1 Для любых двух многочленов |
f (x) и |
g(x) можно найти |
|
такие многочлены q(x) и r(x) , что f (x) = g(x)q(x) + r(x) , |
(3.6) |
причем степень r(x) меньше степени g(x) или же r(x) = 0 . Многочлены q(x) и r(x) , удовлетворяющие этому условию (3.6), определяются однозначно.
Доказательство. Докажем сначала вторую половину теоремы. Пусть
существуют еще многочлены q(x) и r(x) также удовлетворяющие равенству
|
(3.6), т.е. |
|
|
f (x) = g(x)q(x) + r(x) , |
(3.7) |
причем степень r(x) снова меньше степени g(x) . Приравнивая друг другу правые части равенств (3.6) и (3.7), получим:
g( x )(q( x ) − q( x ))= r( x ) − r( x ) .
Степень правой части этого равенства меньше степени g(x) , степень же левой части была бы при q(x) − q(x) ≠ 0 больше или равна степени g(x) . Поэтому должно быть q(x) − q(x) = 0 , т.е. q(x) = q(x) , а тогда и r(x) = r(x) . Что и
требовалось доказать.
Переходим к доказательству первой половины теоремы. Пусть многочлены f (x) и g(x) имеют соответственно степени п и s . Если n < s , то
можно положить q(x) = 0 , r(x) = f (x) . Если же n ≥ s , то воспользуемся тем же
методом, каким производится деление многочленов с действительными коэффициентами, расположенными по убывающим степеням неизвестного. Пусть
f (x) = a0 xn + a1xn−1 +… + an−1x + an , a0 ≠ 0 ,
52
|
g(x) = b xs + b xs −1 |
+… + b |
x + b , |
b ≠ 0 . |
||||
|
0 |
1 |
a0 |
s −1 |
s |
0 |
||
|
Полагая |
f (x) − |
xn−s g(x) = f (x) , |
(3.8) |
||||
|
b0 |
1 |
||||||
мы получим многочлен, степень которого меньше п. Обозначим эту степень через
|
n1 , а старший коэффициент многочлена f1(x) |
— через a1,0 . Положим, далее, если |
||||||||||||
|
все еще n1 ≥ s , |
|||||||||||||
|
f1 (x) − |
a1,0 |
xn1 −s g(x) = f2 (x) , |
(3.8)1B B |
||||||||||
|
b0 |
степень, а через a2,0 |
||||||||||||
|
обозначим через n2 — |
— |
старший коэффициент многочлена |
|||||||||||
|
f2 (x) , положим затем |
|||||||||||||
|
a2,0 |
n −s |
g(x) = f3 (x) , |
(3.8)2B B |
||||||||||
|
f2 (x) − |
x 2 |
||||||||||||
|
b0 |
|||||||||||||
|
и т.д. |
|||||||||||||
|
f2 (x), … убывают, |
n > n1 > n2 >…, то |
||||||||||||
|
Так как степени многочленов f1(x), |
|||||||||||||
|
мы дойдем после конечного числа шагов до такого многочлена |
fk (x) , |
||||||||||||
|
fk −1(x) − |
ak −1,0 |
x |
n |
k −1 |
−s |
g(x) = fk (x) |
(3.8)kB -1B |
||||||
|
b0 |
|||||||||||||
степень которого nk меньше s , после чего наш процесс останавливается. Складывая теперь равенства (3.8), (3.8)1B ,B …, (3.8)kB -1,B мы получим:
|
a |
0 |
n−s |
a1,0 |
n |
−s |
ak −1, 0 |
n |
−s |
||||||||||||||||
|
1 |
k −1 |
|||||||||||||||||||||||
|
f (x) − |
x |
+ |
x |
+… |
+ |
x |
g(x) = fn (x) , |
|||||||||||||||||
|
b |
b |
b |
||||||||||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||||||
|
т.е. многочлены |
a1,0 |
ak −1, 0 |
||||||||||||||||||||||
|
a |
0 |
n−s |
n −s |
n |
−s |
|||||||||||||||||||
|
q(x) = |
x |
+ |
x 1 |
+… + |
x |
k −1 |
, |
|||||||||||||||||
|
b |
b |
b |
||||||||||||||||||||||
|
0 |
0 |
0 |
r(x) = fk (x)
действительно удовлетворяют равенству (3.6), причем степень r(x) на самом деле меньше степени g(x) , что и требовалось доказать.
Заметим, что если многочлены f (x) и g(x) с целыми коэффициентами и старший коэффициент многочлена g(x) равен единице, то многочлены q(x) и r(x) будут иметь только целые коэффициенты. При делении столбиком придется умножать многочлен g(x) лишь на целые кратные степеней переменной х.
Отметим также, что при делении на многочлен первой степени остаток является константой.
53
3.2 Свойства делимости многочленов
Пусть f (x) и ϕ(x) — ненулевые многочлены, тогда многочлен f (x) делится нацело на многочлен ϕ(x) , если остаток от деления f (x) на ϕ(x) равен
нулю.
В этом случае многочлен ϕ(x) называется делителем многочлена f (x) .
Теорема 3.2 Многочлен ϕ(x) тогда и только тогда будет делителем многочлена f (x) , если существует многочлен ψ (x) , удовлетворяющий равенству
|
f (x) =ϕ(x)ψ (x) . |
(3.9) |
|
Доказательство. Если ϕ(x) является делителем для |
f (x) , то в качестве |
|
ψ (x) следует взять частное от деления f (x) на ϕ(x) . |
Обратно, пусть многочлен ψ (x) , удовлетворяющий равенству (3.9), существует. Из доказанной ранее единственности многочленов q(x) и r(x) , удовлетворяющих равенству f (x) =ϕ(x)q(x) + r(x) и условию, что степень r(x) меньше степени ϕ(x) , в нашем случае следует, что частное от деления f (x) на ϕ(x) равно ψ (x) , а остаток равен нулю.
Очевидно, что если f (x) =ϕ(x)ψ (x) , то делителем для f (x) будет как ϕ(x) , так и ψ (x) и что степени ϕ(x) и ψ (x) не могут быть больше степени f (x) .
Очевидно, что если многочлен f (x) и его делитель ϕ(x) имеют оба рациональные или действительные коэффициенты, то и многочлен ψ (x) также
будет иметь рациональные, или, соответственно, действительные коэффициенты, так как он разыскивается при помощи алгоритма деления.
Основные свойства делимости многочленов
1. Если f (x) делится на g(x) , а g(x) делится на h(x) , то f (x) будет делится на h(x) .
В самом деле, по условию f (x) = g(x)ϕ(x) и g(x) = h(x)ψ (x) , а поэтому
f(x) = h(x)[ϕ(x)ψ (x)].
2.Если f (x) и g(x) делятся на ϕ(x) , то их сумма и разность также делятся на ϕ(x) .
|
Действительно, из равенства f (x) =ϕ(x)ψ (x) и |
g(x) =ϕ(x)χ(x) вытекает |
|
f (x) ± g(x) =ϕ(x)[ψ (x) ± χ(x)]. |
|
|
3. Если f (x) делится на ϕ(x) , то произведение |
f (x) на любой многочлен |
|
g(x) также будет делиться на ϕ(x) . |
|
|
Действительно, если f (x) =ϕ(x)ψ (x) , то f (x)g(x) =ϕ(x)[ψ (x)g(x)]. |
|
|
Из 2 и 3 вытекает следующее свойство: |
fk (x) делится на ϕ(x) , то |
|
4. Если каждый из многочленов f1(x), f2 (x), …, |
на ϕ(x) будет делиться и многочлен f1(x)g1(x) + f2 (x)g2 (x) + … + fk (x)gk (x) , где g1(x), g2 (x), …, gk (x) — произвольные многочлены.
54
|
5. Всякий многочлен |
f (x) делится на любой многочлен нулевой степени. |
||||||||||||||||||||
|
Действительно, |
если |
f (x) = a |
0 |
xn + a xn−1 |
+… + a |
n |
−1 |
x + a |
n |
, |
а |
с — |
|||||||||
|
1 |
|||||||||||||||||||||
|
произвольное число, |
не равное |
нулю, т.е. произвольный |
многочлен |
нулевой |
|||||||||||||||||
|
a |
0 |
a |
a |
n |
|||||||||||||||||
|
степени, то f (x) = c |
xn + |
1 |
xn−1 +… + |
. |
|||||||||||||||||
|
c |
c |
||||||||||||||||||||
|
6. |
c |
||||||||||||||||||||
|
Если f (x) |
делится на |
ϕ(x) , то |
f (x) делится и на cϕ(x) , |
где с – |
|||||||||||||||||
|
произвольное число, отличное от нуля. |
f (x) =ϕ(x)ψ (x) |
следует |
равенство |
||||||||||||||||||
|
В |
самом |
деле, |
из |
равенства |
|||||||||||||||||
|
f (x) = [cϕ(x)] [c−1ψ (x)]. |
|||||||||||||||||||||
|
7. Многочлены cf (x) , |
c ≠ 0 , и только они, будут делителями многочлена |
||||||||||||||||||||
|
f (x) , имеющими такую же степень, что и f (x) . |
|||||||||||||||||||||
|
Действительно, |
f (x) = c−1[cf (x)], т.е. |
f (x) делится на cf (x) . |
|||||||||||||||||||
|
Если, с другой стороны, |
f (x) делится на ϕ(x) , причем степени |
f (x) и |
|||||||||||||||||||
|
ϕ(x) совпадают, то степень частного от деления |
f (x) |
на |
ϕ(x) |
должна быть |
|||||||||||||||||
|
равной нулю, т.е. |
f (x) = dϕ(x) , d ≠ 0 , откуда ϕ(x) = d −1 f (x) . |
||||||||||||||||||||
|
Отсюда вытекает следующее свойство: |
|||||||||||||||||||||
|
8. |
Тогда и только тогда многочлены f (x) , |
g(x) |
одновременно делятся |
||||||||||||||||||
|
друг на друга, если g(x) = cf (x) , c ≠ 0 . |
|||||||||||||||||||||
|
Наконец, из 8 и 1 вытекает свойство |
|||||||||||||||||||||
|
9. |
Всякий делитель одного из двух многочленов |
f (x) , cf (x) , |
где c ≠ 0 , |
будет делителем и для другого многочлена.
Процесс деления многочленов «столбиком» рассмотрим на практических занятиях (см. тему «Многочлены»).
3.3 Корни многочлена. Теорема Безу
Значением многочлена
|
f (x) = a |
0 |
xn + a xn−1 |
+… + a |
n |
(3.10) |
|||||||||
|
1 |
cn + a cn−1 |
|||||||||||||
|
при x = c называется результат вычисления a |
0 |
+ … + a |
n |
. |
||||||||||
|
1 |
||||||||||||||
|
НапримерU |
,U найти значения многочлена |
f (x) = x2 − 3x +1, при x = 0 , |
x = 2. |
|||||||||||
|
Вместо переменной подставляем в выражение |
f (x) |
заданные x = 0 , |
x = 2 и |
|||||||||||
|
производим |
соответствующие |
вычисления, |
т.е. |
f (0) = 02 − 3 0 +1, |
f (0) =1, |
|||||||||
|
аналогично |
f (2) = 22 − 3 2 +1, f (2) = 0 . |
|||||||||||||
|
Т.е. значение заданного многочлена при x = 0 равно единице, при x = 2 — |
||||||||||||||
|
нулю. |
ϕ(x) = f (x) + g(x) , |
ψ (x) = f (x)g(x) , |
то |
|||||||||||
|
Очевидно, |
что |
если |
||||||||||||
|
ϕ(c) = f (c) + g(c) , ψ (c) = f (c) g(c) . |
||||||||||||||
|
Корнем многочлена |
f (x) |
называется такое x = c , при котором значение |
||||||||||||
|
многочлена равно нулю. |
55
|
Таким образом, в примере разобранном |
выше x = 2 является |
корнем |
|||||||
|
многочлена |
f (x) = x2 − 3x +1. |
||||||||
|
Важную роль в процессе нахождения корней многочлена играет теорема |
|||||||||
|
Безу и ее следствия. |
|||||||||
|
Теорема Безу. Число x0 тогда и только |
тогда |
является |
корнем |
||||||
|
многочлена |
f (x) , |
когда |
существует |
такой |
многочлен |
q(x) , |
что |
||
|
f (x) = (x − x0 )q(x) . |
для f (x) , |
то, |
|||||||
|
Доказательство. Если имеет место такое |
представление |
||||||||
|
подставляя в него x = x0 , получим: f (x0 ) = 0 . |
f (x) . Разделим многочлен |
f (x) на |
|||||||
|
Обратно, пусть x0 — корень многочлена |
|||||||||
|
многочлен |
x − x0 : |
f (x) = q(x)(x − x0 ) + r . Здесь r |
— действительное число. |
Оно |
|||||
|
равно нулю. В |
самом |
деле, подставим |
в |
это |
равенство |
x = x0 : |
|||
|
0 = f (x0 ) = q(x0 )(x0 − x0 ) + r r = 0 . |
Следствия теоремы Безу:
1 Остаток от деления многочлена f (x) на двучлен (x − c) равен значению
|
многочлена при x = c , то есть r = f (c) . |
|||||||||||||||||
|
2 При делении многочлена |
f (x) |
на двучлен |
вида |
ax + b |
получается |
||||||||||||
|
остаток, равный значению этого многочлена при x = − |
b |
, т.е. |
− |
b |
|||||||||||||
|
a |
r = f |
. |
|||||||||||||||
|
a |
|||||||||||||||||
|
НапримерU |
,U используя второе следствие из теоремы Безу найдем остаток от |
||||||||||||||||
|
деления многочлена |
f (x) = 2x3 − x2 + 4x −1 на двучлен 2x −1. |
||||||||||||||||
|
Решение. |
1 |
1 3 |
1 2 |
1 |
. Таким образом, искомый |
||||||||||||
|
r = |
f |
= 2 |
− |
+ 4 |
−1 =1 |
||||||||||||
|
2 |
2 |
2 |
2 |
остаток равен единице.
Использование теоремы Безу в задачах разложения многочлена на множители подробно рассматривается в практических разработках.
Как мы отметили выше, деление многочлена на многочлен производится как «обычное» деление, т.е. столбиком. Существует метод Горнера, дающий возможность достаточно несложным образом разделить многочлены любой степени на многочлен первой степени, т.е. на двучлен.
3.4 Метод Горнера
Пусть дан многочлен
|
f (x) = a |
0 |
xn + a xn−1 + a |
2 |
xn−2 +… + a |
n |
(3.11) |
|
|
1 |
|||||||
|
и пусть результат его деления на двучлен (x − c) есть |
|||||||
|
f (x) = (x − c)q(x) + r , |
(3.12) |
||||||
|
где q(x) = b xn−1 + b xn−2 |
+ b xn−3 + … + b |
. |
|||||
|
0 |
1 |
2 |
n −1 |
Сравнивая коэффициенты при одинаковых степенях xi в (3.12), получаем:
56

a0 = b0 ,
a1 = b1 − cb0 , a2 = b2 − cb1 ,
…………..
an−1 = bn−1 − cbn−2 , an = r − cbn −1 .
Отсюда следует, что b0 = a0 , bk = cbk −1 + ak , k =1, 2,…, n −1, т.е. коэффициенты bk получается умножением предыдущего коэффициента ak ;
наконец, r = cbn −1 + an , т.е. и остаток r , равный, как мы знаем, f (c) , получается
по этому же закону. Таким образом, коэффициенты частного и остаток можно последовательно получать при помощи однотипных вычислений, которые располагаются в схему, называемую схемой Горнера.
Для нахождения коэффициентов bn −1 , bn−2 , …, b1 , b0 и остатка r схема Горнера выглядит следующим образом:
|
a0 |
a1 |
a2 |
a3 |
… an −1 |
an |
|
|
+ |
+ |
+ |
… + |
+ |
||
|
сb0 |
сb1 |
сb2 |
… сbn−2 сbn −1 |
|||
|
с |
b0 |
b1 |
b2 |
b3 |
… bn −1 |
r |
В этой схеме, начиная с коэффициента b1 , каждое число третей строки
получается из предыдущего числа этой строки умножением на число c и прибавлением к полученному результату соответствующего числа первой строки,
|
стоящего над искомым числом. |
||||||||||
|
НапримерU |
,U |
используя |
схему |
Горнера, |
разделим |
многочлен |
||||
|
2x2 − 3x3 − x + x5 +1 на x +1. |
||||||||||
|
Сначала запишем делимое в каноническом виде, то есть в виде |
||||||||||
|
x5 + 0 x4 − 3x3 + 2x2 − x +1. |
||||||||||
|
Так как в нашем случае (x − c) = (x +1) , то c = −1. |
||||||||||
|
Применяя схему Горнера, имеем |
||||||||||
|
1 |
0 |
–3 |
2 |
–1 |
1 |
|||||
|
+ |
+ |
+ |
+ |
+ |
||||||
|
–1 |
1 |
2 |
–4 |
5 |
||||||
|
–1 |
1 |
–1 |
–2 |
4 |
–5 |
6 |
Итак, получим частное q(x) = x4 − x3 − 2x2 + 4x − 5 , остаток r = 6 . Таким образом, x5 − 3x3 + 2x2 − x +1 = (x +1)(x4 − x3 − 2x2 + 4x − 5) + 6 .
Метод деления многочлена на двучлен с использованием схемы Горнера носит название метода Горнера.
3.5 Основная теорема алгебры
57
Занимаясь в предыдущем параграфе корнями многочленов, мы не ставили вопроса о том, всякий ли многочлен обладает корнями. Известно, что существуют многочлены с действительными коэффициентами, не имеющие действительных
корней; x2 +1 — один из таких многочленов. Можно было бы ожидать, что существуют многочлены, не имеющие корней даже среди комплексных чисел, особенно если рассматриваются многочлены с любыми комплексными коэффициентами. Если бы это было так, то система комплексных чисел нуждалась бы в дальнейшем расширении. На самом деле, однако, справедлива следующая основная теорема алгебры:
Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Эта теорема является одним из крупнейших достижений всей математики и находит применения в самых различных областях науки. На ней основана, в частности, вся дальнейшая теория многочленов с числовыми коэффициентами, и потому эту теорему называли раньше (а иногда называют и теперь) «основной теоремой высшей алгебры». В действительности, однако, основная теорема не является чисто алгебраической. Все ее доказательства, — а их, после Гаусса, впервые доказавшего эту теорему в конце XVIII века, было найдено очень много, — используют в большей или меньшей мере так называемые топологические свойства действительных и комплексных чисел, т. е. свойства, связанные с непрерывностью.
3.6 Следствия из основной теоремы алгебры
Пусть дан многочлен n -й степени, n ≥1,
|
f (x)= a |
0 |
xn + a xn−1 |
+… + a |
n−1 |
x + a |
n |
(3.13) |
|
1 |
с любыми комплексными коэффициентами. Основная теорема о существовании корня позволяет утверждать существование для f (x) корня α1 комплексного или
действительного. Поэтому многочлен f (x) обладает разложением
f (x)= (x −α1 )ϕ(x).
Коэффициенты многочлена ϕ(x) снова являются действительными или комплексными числами, и поэтому ϕ(x) обладает корнем α2 , откуда
f (x)= (x −α1 )(x −α2 )ψ (x).
Продолжая так далее, мы придем после конечного числа шагов к разложению многочлена n -й степени в произведение n линейных множителей,
|
f (x)= a0 (x −α1 )(x −α2 )…(x −αn ). |
(3.14) |
|
Коэффициент a0 появился по следующей причине: если бы |
справа в |
выражении (3.14) стоял некоторый коэффициент b, то после раскрытия скобок старший член многочлена f (x) имел бы вид bx , хотя па самом деле, ввиду (3.13),
им является член a0 xn . Поэтому b = a0 .
58
f (x)ϕ(x)= g(x)ϕ(x)
|
Разложение (3.14) является для многочлена f (x) |
единственным, с |
|
точностью до порядка сомножителей, разложением такого типа. |
|
|
Пусть, в самом деле, имеется еще разложение |
|
|
f (x)= a0 (x − β1 )(x − β2 )…(x − βn ). |
(3.15) |
|
Из (3.14) и (3.15) следует равенство |
|
|
(x −α1 )(x −α2 )…(x −αn )= (x − β1 )(x − β2 )…(x − βn ). |
(3.16) |
Если бы корень αi был отличен от всех β j , j =1, 2, …, n , то, подставляя αi вместо неизвестного в (3.16), мы получили бы слева нуль, а справа число,
отличное от нуля. Таким образом, всякий корень αi равен некоторому корню β j
и обратно.
Отсюда еще не вытекает совпадение разложений (3.14) и (3.15). Действительно, среди корней αi , i =1, 2,…, n , могут быть равные между собой.
Пусть, например, s этих корней равны α1 и пусть, с другой стороны, среди корней β j , j =1, 2, …, n , содержится t равных корню α1 . Нужно показать, что
s = t .
Так как степень произведения многочленов равна сумме степеней сомножителей, то произведение двух многочленов, отличных от нуля, не может равняться нулю. Отсюда вытекает, что если два произведения многочленов равны друг другу, то обе части равенства можно сократить на общий множитель:
если
и ϕ(x)≠ 0 , то из
[f (x)− g(x)]ϕ(x)= 0 ,
следует f (x)− g(x)= 0 , т.е. f (x)= g(x).
Применим это к равенству (3.16). Если, например, s > t то, сокращая обе части равенства (3.16) на множитель (x −α1 )t , мы придем к равенству, левая часть которого еще содержит множитель x −α1 , а правая его не содержит. Выше
показано, однако, что это приводит к противоречию. Таким образом, единственность разложения (3.14) для многочлена f (x) доказана.
Объединяя вместе одинаковые множители, разложение (3.14) можно
|
переписать в виде |
|||||||||
|
f (x)= a |
0 |
(x − α )k1 |
(x − α |
2 |
)k2 |
…(x − α |
l |
)ki , |
(3.17) |
|
1 |
|||||||||
|
где k1 + k2 + … + kn = n . |
|||||||||
|
При этом предполагается, что среди корней α1 , α2 , …, αl |
уже нет равных. |
||||||||
|
Всякий |
многочлен |
f (x) |
степени n , n ≥1, |
с любыми числовыми |
коэффициентами имеет n корней, если каждый из корней считать столько раз, какова его кратность.
Заметим, что утверждение справедливо и при n = 0 , так как многочлен нулевой степени не имеет корней. Это утверждение неприменимо лишь к многочлену 0, не имеющему степени и равному нулю при любом значении х.
59

Теорема 3.3 Если многочлены f (x) и g(x), степени которых не
превосходят n , имеют равные значения более чем при n различных значениях неизвестного, то f (x)= g(x).
Действительно, многочлен f (x)− g(x) имеет при наших предположениях
более чем n корней, а так как его степень не превосходит n , то должно иметь место равенство f (x)− g(x)= 0 .
Таким образом, учитывая, что различных чисел бесконечно много, можно утверждать, что для любых двух различных многочленов f (x) и g(x) найдутся
такие значения с неизвестного х, что f (c)≠ g(c). Такие с можно найти не только
среди комплексных чисел, но и среди действительных, среди рациональных и даже среди целых чисел.
3.7 Формулы Вьета
Пусть дан многочлен f (x) степени n со старшим коэффициентом 1,
|
f |
(x)= xn + a xn−1 |
+ a |
2 |
xn−2 +… + a |
n−1 |
x + a |
n |
, |
(3.18) |
|
1 |
f (x) обладает следующим |
||||||||
|
и пусть |
α1 , α2 , …, |
αn |
1) |
.PT |
Тогда |
||||
|
— его корниTP |
разложением:
f (x)= (x −α1 )(x −α2 )…(x −αn ).
Перемножая скобки, стоящие справа, а затем приводя подобные члены и сравнивая полученные коэффициенты с коэффициентами из (3.18), мы получим следующие равенства, называемые формулами Вьета и выражающие коэффициенты многочлена через его корни:
a1 = −(α1 +α2 + … +αn ),
a2 =α1α2 +α1α3 + … +α1αn +α2α3 + … +αn −1αn ,
a3 = −(α1α2α3 +α1α2α4 + … +αn−2αn −1αn ),
…………………………………………….
an −1 =( −1)n−1(α1α2 …αn −1 + α1α2 …αn −2αn + … + α2α3 …αn ), an = (−1)nα1α2…αn .
Таким образом, в правой части k -гo равенства, k =1, 2, …, n , стоит сумма
всевозможных произведений по k корней, взятая со знаком плюс или минус, в зависимости от четности или нечетности k .
При n = 2 эти формулы превращаются в известную из элементарной
|
алгебры связь между корнями и коэффициентами квадратного многочлена. При |
||
|
n = 3 , т. е. для кубичного многочлена, эти формулы принимают вид |
||
|
a1 = −(α1 +α2 +α3 ), |
a2 =α1α2 +α1α3 +α2α3 , |
a3 = −α1α2α3 . |
|
Формулы Вьета облегчают написание многочлена по заданным его |
||
|
корням. Например, найдем |
многочлен f (x) четвертой степени, имеющий |
простыми корнями числа 5 и − 2 и двукратным корнем число 3. Мы получим:
1)PT TP Каждый кратный корень взят здесь соответствующее число раз.
60

a1 = −(5 − 2 + 3 + 3)= −9 ,
a2 = 5 (− 2)+ 5 3 + 5 3 + (− 2) 3 + (− 2) 3 + 3 3 =17 ,
a3 = −[5 (− 2) 3 + 5 (− 2) 3 + 5 3 3 + (− 2) 3 3]= 33 , a4 = 5 (− 2) 3 3 = −90 ,
а поэтому
f (x)= x4 − 9x3 +17x2 + 33x − 90 .
Если старший коэффициент a0 многочлена f (x) отличен от 1, то для
применения формул Вьета необходимо сначала разделить все коэффициенты на a0 , что не влияет на корни многочлена. Таким образом, в этом случае формулы
Вьета дают выражение для отношений всех коэффициентов к старшему.
3.8 Многочлены с действительными коэффициентами. Разложение многочлена на множители
Пусть многочлен с действительными коэффициентами f (x)= xn + a1xn−1 + a2 xn−2 +… + an−1x + an
имеет комплексный корень α , т. е.
a0αn + a1αn−1 +… + an−1α + an = 0 .
Последнее равенство не нарушится, если в нем все числа заменить на сопряженные. Однако все коэффициенты a0 , a1 , …, an −1 , an , a также число 0,
стоящее справа, будучи действительными, останутся при этой замене без изменения. Следовательно, справедливо равенство
a0 αn + a1αn−1 + … + an−1α + an = 0 , т.е. f (α)= 0 .
Таким образом, если комплексное (но не действительное) число α служит корнем многочлена f (x) с действительными коэффициентами, то корнем для
f (x) будет и сопряженное число α .
Многочлен f (x) будет делиться, следовательно, на квадратный трехчлен
|
ϕ(x)= (x −α)(x − |
)= x2 − (α + |
)x +αα |
, |
(3.19) |
||
|
α |
α |
коэффициенты которого действительны. Пользуясь этим, докажем, что корни α и
α имеют в многочлене f (x) одну и ту же кратность.
Пусть, в самом деле, эти корни имеют соответственно кратности k и l и пусть, например, k > l . Тогда f (x) делится на l -ю степень многочлена ϕ(x),
f (x)=ϕl (x)q(x).
Многочлен q(x), как частное двух многочленов с действительными
коэффициентами, также имеет действительные коэффициенты, но, в противоречие с доказанным выше, он имеет число α своим (k − l) кратным
корнем, тогда как число α не является для него корнем. Отсюда следует, что k = l .
Таким образом, теперь можно сказать, что комплексные корни всякого многочлена с действительными коэффициентами попарно сопряжены. Отсюда и
61
из доказанной выше единственности разложений вида (3.14) вытекает справедливость следующей теоремы.
Теорема 3.4 Всякий многочлен f (x) с действительными коэффициентами
представим, притом единственным способом (с точностью до порядка множителей), в виде произведения своего старшего коэффициента a0 и
нескольких многочленов с действительными коэффициентами, линейных вида x −α , соответствующих его действительным корням, и квадратных вида (3.19), соответствующих парам сопряженных комплексных корней.
Для дальнейшего полезно подчеркнуть, что среди многочленов с действительными коэффициентами и со старшим коэффициентом 1, неразложимыми на множители меньшей степени или, как мы будем говорить, неприводимыми, являются лишь линейные многочлены вида x −α и квадратные многочлены вида (3.19).
3.9 Наибольший общий делитель многочленов. Алгоритм Евклида
Многочлен ϕ(x) называется общим делителем для заданных многочленов f (x) и g(x) , если он является делителем для каждого из этих многочленов.
Согласно пятому свойству делимости многочленов можно заключить, что к числу общих делителей многочленов f (x) и g(x) принадлежат все многочлены
нулевой степени (т.е. числа).
Два многочлена f (x) и g(x) называются взаимно простыми, если они не
имеют никаких общих делителей кроме многочленов нулевой степени.
Наибольшим общим делителем (коротко НОД) отличных от нуля многочленов f (x) и g(x) называется такой многочлен d (x) , который является их
общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов.
Обозначение: (f (x), g(x)) — наибольший общий делитель многочленов f (x) и g(x) .
Для отыскания НОД удобно пользоваться алгоритмом Евклида (или
алгоритмом последовательного деления).
Алгоритм Евклида
Суть алгоритма Евклида, с помощью которого находится наибольший общий делитель заданных многочленов f (x) и g(x) — (f (x), g(x)), состоит в
последовательном делении сначала многочлена f (x) на g(x) , затем многочлена g(x) на полученный от первого деления остаток r1(x) , затем r1(x) на полученный от второго деления остаток r2 (x) и т.д. Поскольку степени
остатков все время понижаются, то эта цепочка последовательных делений остановится в тот момент, когда деление совершится нацело. Тот остаток rk (x) , на который нацело разделится предыдущий rk −1(x) , и будет
62
|
наибольшим общим делителем многочленов |
f (x) и g(x) . |
||||||
|
Запишем алгоритм Евклида следующей цепочкой неравенств: |
|||||||
|
f (x) = g(x)q1(x) + r1(x), |
|||||||
|
g(x) = r1(x)q2 (x) + r2 (x), |
|||||||
|
r1(x) = r2 (x)q3 (x) + r3 (x), |
|||||||
|
……………………………. |
(3.20) |
||||||
|
r |
(x) = r |
(x)q |
k −1 |
(x) |
+ r |
(x), |
|
|
k −3 |
k −2 |
k −1 |
|||||
|
rk −2 (x) = rk −1(x)qk (x) + rk (x), |
|||||||
|
rk −1(x) = rk (x)qk +1(x). |
|||||||
Последнее равенство показывает, что rk (x) служит делителем для rk −1(x) . Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на rk (x) , а поэтому rk (x) будет делителем и для rk −2 (x) . Далее, таким же
|
путем, поднимаясь |
вверх, мы получим, что rk (x) является делителем и для |
|
rk −3 (x) , …, r2 (x) , |
r1(x) . Отсюда, ввиду второго равенства, будет следовать, что |
rk (x) служит делителем для g(x) , а поэтому, на основании первого равенства, — и для f (x) . Таким образом, rk (x) является общим делителем для f (x) и g(x) .
Возьмем теперь произвольный общий делитель ϕ(x) многочленов f (x) и g(x) . Так как левая часть и первое слагаемое правой части первого из равенств (3.20) делятся на ϕ(x) , то r1(x) также будет делиться на ϕ(x) . Переходя ко второму и следующему равенствам, мы таким же способом получим, что на ϕ(x)
|
делятся |
многочлены r2 ( x ), r3( x ), …. Наконец, если уже будет доказано, что |
|
rk −2 (x) |
и rk −1(x) делятся на ϕ(x) , то из предпоследнего равенства мы получим, |
что rk (x) делится на ϕ(x) . Таким образом, rk ( x ) на самом деле будет наибольшим общим делителем для f (x) и g(x) .
Из доказательства справедливости алгоритма Евклида следует и справедливость следующих утверждений:
1 Любые два многочлена обладают наибольшим общим делителем.
2Если многочлены f (x) и g(x) имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными.
3Наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени, т.е. если d (x) есть (f (x), g(x)), то и
многочлен cd(x) также является (f (x), g(x)) в связи с третьим утверждением.
Условимся, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице, а значит два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице.
63
|
НапримерU |
,U |
найдем |
наибольший |
общий |
делитель |
многочленов |
|||||
|
f (x) = x3 − 4x2 + 4x −1 и |
g(x) = x2 + 2x − 3 . |
Следуем |
строго |
по алгоритму |
|||||||
|
Евклида |
|||||||||||
|
1) f (x) : g(x) |
|||||||||||
|
− |
x3 − 4x2 + 4x −1 |
x2 + 2x − 3 |
|||||||||
|
x3 + 2x2 − 3x |
|||||||||||
|
x − 6 |
|||||||||||
|
− 6x2 + 7x −1 |
|||||||||||
|
− 6x2 −12x +18 |
|||||||||||
|
19x −19 |
Так как f (x) = g(x) q(x) + r1(x) , т.е. x3 − 4x2 + 4x −1=( x2 + 2x −3)( x −6 ) +
+(19x −19) , следовательно, r1(x) =19x −19 .
2)g(x) : r1(x)
|
_ x2 + 2x − 3 |
19x −19 |
||||||||||||
|
x2 − x |
|||||||||||||
|
1 |
x + |
3 |
|||||||||||
|
19 |
19 |
||||||||||||
|
3x − 3 |
|||||||||||||
|
3x − 3 |
|||||||||||||
|
0 |
|||||||||||||
|
т.е. получим, что |
|||||||||||||
|
1 |
3 |
||||||||||||
|
g(x) = r |
(x) |
x + |
. |
||||||||||
|
19 |
|||||||||||||
|
1 |
19 |
Следовательно, наибольшим общим делителем многочленов f (x) и g(x)
служит двучлен 19x −19 . На основании утверждения 3 наибольшим общим делителем многочлен f (x) и g(x) будем считать многочлен ( x −1).
Займемся дальнейшим исследованием делимости многочленов.
Теорема 3.5 Если d (x) есть наибольший общий делитель многочленов
|
f (x) и g(x) , то можно найти такие многочлены u(x) и v(x) , что |
|
|
f (x)u(x) + g(x)v(x) = d(x) . |
(3.21) |
Доказательство. Можно считать при этом, если степени многочленов f (x) и g(x) больше нуля, то степень u(x) меньше степени g(x) , а степень v(x)
|
меньше степени f (x) . |
||
|
Доказательство основано |
на равенствах |
(3.20). Если мы учтем, что |
|
rk (x) = d (x) , и положим u1(x) =1, |
v1(x) = −qk (x) , |
то предпоследнее из равенств |
|
(3.20) даст: |
d (x) = rk −2 (x)u1(x) + rk −1(x)v1(x) .
64
Подставляя сюда выражение rk −1(x) через rk −3 (x) и rk −2 (x) из
предшествующего равенства, мы получим: d(x) = rk −3 (x)u2 (x) + rk −2 (x)v2 (x) ,
где, очевидно, u2 (x) = v1(x) , v2 (x) = u1(x) − v1(x)qk −1(x) . Продолжая подниматься вверх по равенствам, мы придем, наконец, к доказываемому равенству.
Для доказательства второго утверждения теоремы предположим, что многочлены u(x) и v(x) , удовлетворяющие равенству (3.21), уже найдены, но,
например, степень u(x) больше или равна степени g(x) . Делим u(x) на g(x) : u(x) = g(x)q(x) + r(x) ,
где степень r(x) меньше степени g(x) , и подставляем это выражение в (3.21). Мы получим равенство f (x)(g(x)q(x)+ r(x))+ g(x)v(x)= d (x), или
f (x)r(x) + g(x)[v(x) + f (x)q(x)]= d (x) .
Степень множителя, стоящего при f (x) , уже меньше степени g(x) . Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени f (x) , так как в противном случае степень второго слагаемого левой части была бы не меньше степени произведения g(x) f (x) , а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени g(x) f (x) , тогда как многочлен d(x) заведомо имеет, при наших предположениях, меньшую степень. Теорема доказана.
Одновременно мы получаем, что если многочлены f (x) и g(x) имеют рациональные или действительные коэффициенты, то и многочлены u( x ) и v( x ), удовлетворяющие равенству (3.21) можно подобрать так, что их коэффициенты будут рациональными или, соответственно, действительными.
Представление (3.21) называется представлением d( x) (наибольшего общего делителя f (x) и g(x) ) в линейной форме.
Следствие. Многочлены f (x) и g(x) тогда и только тогда взаимно просты, если можно найти многочлены u(x) и v(x) , удовлетворяющие равенству
|
f (x)u(x) + g(x)v(x) =1. |
(3.22) |
Теоремы о взаимно простых многочленах
1 Если многочлен f (x) взаимно прост с каждым из многочленов ϕ(x) и ψ (x) , то он взаимно прост и с их произведением.
Доказательство. Поскольку по условию многочлен f (x) взаимно прост с многочленом ϕ(x) , то на основании формулы (3.22) существуют такие многочлены u(x) и v(x) , что
f (x)u(x) +ϕ(x)v(x) =1.
Умножим это равенство на ψ (x) :
f (x)[u(x)ψ (x)]+ [ϕ(x)ψ (x)]v(x) =ψ (x) ,
65

из полученного следует, что всякий общий делитель f (x) и ϕ(x) ψ (x) был бы делителем и для ψ (x) ; однако по условию (f (x),ψ (x))=1.
2 Если произведение многочленов f (x) и g(x) делится на ϕ(x) , но f (x) и ϕ(x) взаимно просты, то g(x) делится на ϕ(x) .
Доказательство. Поскольку f (x) и ϕ(x) — взаимно просты то, согласно (3.22), верно что f (x)u(x) +ϕ(x)v(x) =1. Умножим это равенство на g(x) , имеем:
[f (x)g(x)]u(x) +ϕ(x)[v(x)g(x)]= g(x) .
Так как оба слагаемых левой части этого равенства делятся на ϕ(x) , то следовательно и g(x) делится на ϕ(x) .
3 Если многочлен f (x) делится на каждый из многочленов ϕ(x) и ψ (x) , которые между собой взаимно просты, то f (x) делится и на их произведение.
Доказательство. f (x) = ϕ(x) ϕ(x) , так что произведение, стоящее справа, делится на ψ (x) . Поэтому, по второй теореме, ϕ(x) делится на ψ (x) ,
ϕ(x) =ψ (x)ψ (x) , откуда f (x) =[ϕ(x)ψ (x)]ψ (x) .
Очевидно, что определение наибольшего общего делителя может быть распространено на случай любой конечной системы многочленов.
4 Наибольший общий делитель многочленов f1(x), f2 (x), …, fs (x) равен наибольшему общему делителю многочлена fs (x) и наибольшего общего делителя многочленов f1(x), f2 (x), …, fs −1(x) .
Доказательство. При s = 2 теорема очевидна. Примем, что для случая s −1 она справедлива, т.е. уже доказано существование наибольшего общего делителя
d (x) многочленов f1(x), f2 (x), …, fs −1(x) . Обозначим через d (x) наибольший общий делитель многочленов d (x) и fs (x) . Он будет, очевидно, общим
делителем для всех заданных многочленов. С другой стороны, всякий другой общий делитель этих многочленов будет делителем также и для d (x) , а поэтому и
для d (x) .
В заключении отметим, что система многочленов f1(x), f2 (x), …, fn (x)
называется взаимно простой, если общими делителями многочленов этой системы являются только многочлены нулевой степени.
3.10 Вопросы для самоконтроля
1 Сформулируйте определение многочлена n -й степени от одной переменной.
2Какой вид многочлена называется каноническим?
3Что значит степень многочлена (нулевая степень, двучлен)?
4Какие действия возможны над многочленами?
5Свойства операций сложения и произведения многочленов.
6Сформулируйте условие существования многочлена, обратного данному.
7Что значит разделить многочлены друг на друга?
8Что значит многочлен f (x) делится нацело на многочлен ϕ(x) ?
66
9Сформулируйте и докажите теорему о делителе многочлена.
10Сформулируйте основные 9 свойств делимости многочлена.
11Какое число называется корнем многочлена?
12Сформулируйте и докажите теорему Безу.
13Чему равен остаток от деления многочлена f (x) на двучлен (x − c)?
14Чему равен остаток от деления многочлена f (x) на двучлен (ax + b)?
15Расскажите в чем заключается суть метода Горнера.
16Сформулируйте основную теорему алгебры.
17Сформулируйте и докажите следствие из основной теоремы алгебры.
18Запишите формулы, выражающие коэффициенты многочлена через его корни. Как называются эти формулы?
19Сформулируйте теорему о разложении многочлена с действительными коэффициентами на множители.
20Какие два многочлена называются взаимно простыми?
21Какой многочлен называется общим делителем заданных многочленов?
22Какой многочлен называется наибольшим общим делителем заданных многочленов?
23В чем заключается суть алгоритма Евклида?
24 Что означает представление d( x ) (наибольшего общего делителя f ( x ) и g( x )) в линейной форме.
25Сформулируйте необходимое и достаточное условие того, что многочлены f (x) и g( x ) взаимно просты.
26Докажите теорему о том, что если многочлен f (x) взаимно прост с каждым из многочленов ϕ(x) и ψ (x) , то он взаимно прост и с их произведением.
27Докажите теорему о том, что если произведение многочленов f (x) и g(x) делится на ϕ(x) , но f (x) и ϕ(x) взаимно просты, то g(x) делится на ϕ(x) .
28Докажите теорему о том, что если многочлен f (x) делится на каждый из многочленов ϕ(x) и ψ (x) , которые между собой взаимно просты, то f (x)
делится и на их произведение.
29 Докажите теорему о том, что наибольший общий делитель
|
многочленов |
f1(x), |
f2 (x), …, fs (x) равен |
наибольшему общему делителю |
|
многочлена |
fs (x) |
и наибольшего |
общего делителя многочленов |
|
f1(x), f2 (x), …, |
fs −1(x) . |
30 Какая система многочленов называется взаимно простой?
67
Соседние файлы в предмете Алгебра и начала анализа
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математическая концепция
В математике степень многочлена — это наивысшая из степеней одночленов многочлена (отдельных членов) с ненулевыми коэффициентами. Степень члена — это сумма показателей степени переменных, которые в нем появляются, и, следовательно, является неотрицательным целым числом. Для одномерного полинома степень полинома — это просто наивысший показатель степени, встречающийся в полиноме. Термин порядок использовался как синоним степени, но в настоящее время может относиться к нескольким другим концепциям (см. порядок многочлена (значения) ).
Например, многочлен 7 x 2 y 3 + 4 x — 9, { displaystyle 7x ^ {2} y ^ {3} + 4x-9,}

Чтобы определить степень многочлена, не входящего в стандартную форму, например (x + 1) 2 — (x — 1) 2 { displaystyle (x + 1) ^ {2} — (x-1) ^ {2}}

Содержание
- 1 Имена многочленов по степени
- 2 Примеры
- 3 Поведение при полиномиальных операциях
- 3.1 Сложение
- 3.2 Умножение
- 3.3 Состав
- 4 Степень нулевого многочлена
- 5 Вычисляется из значений функции
- 6 Расширение до многочленов с двумя или более переменными
- 7 Степенная функция в абстрактной алгебре
- 8 См. Также
- 9 Примечания
- 10 Ссылки
- 11 Внешние ссылки
Имена многочленов по степени
Следующие имена присвоены многочленам в соответствии с до их степени:
- Особый случай — ноль (см. § Степень нулевого многочлена ниже)
- Степень 0 — ненулевое константа
- Степень 1 — линейная
- Степень 2 — квадратичная
- Степень 3 — кубическая
- Степень 4 — четверная (или, если все члены имеют четные степень, биквадратная )
- степень 5 — квинтическая
- степень 6 — секстическая (или, реже y, гексик)
- Степень 7 — септический (или, реже, гептический)
Для более высоких степеней имена иногда предлагались, но они используются редко:
- Степень 8 — октическая
- Степень 9 — ноническая
- Степень 10 — децитическая
Имена для ступеней выше трех основаны на латинских порядковых числах и оканчиваются на -ic. Это следует отличать от имен, используемых для количества переменных, arity, которые основаны на латинских распределительных числах и оканчиваются на -ary. Например, многочлен второй степени от двух переменных, такой как x 2 + xy + y 2 { displaystyle x ^ {2} + xy + y ^ {2}}

Примеры
Многочлен (y — 3) (2 y + 6) (- 4 y — 21) { displaystyle (y-3) (2y + 6) ( -4y-21)}

Многочлен (3 z 8 + z 5 — 4 z 2 + 6) + (- 3 z 8 + 8 z 4 + 2 z 3 + 14 z) { displaystyle (3z ^ {8} + z ^ {5} -4z ^ {2} +6) + (- 3z ^ {8} + 8z ^ {4} + 2z ^ {3} + 14z)}

Поведение при полиномиальных операциях
Степень суммы, произведения или композиции двух полиномов сильно зависит от степени входных полиномов.
Сложение
Степень суммы (или разности) двух поли номиналы меньше или равны большей из их степеней; то есть
- deg (P + Q) ≤ max {deg (P), deg (Q)} { displaystyle deg (P + Q) leq max { deg (P), deg (Q) }}
и deg (P — Q) ≤ max {deg (P), deg (Q)} { displaystyle deg (PQ) leq max { deg (P), deg (Q) }}
.
Например, степень (x 3 + x) — (x 3 + x 2) = — x 2 + x { displaystyle (x ^ {3} + x) — (x ^ {3} + x ^ {2}) = — x ^ {2} + x}
Равенство всегда выполняется, если степени полиномов различны. Например, степень (x 3 + x) + (x 2 + 1) = x 3 + x 2 + x + 1 { displaystyle (x ^ {3} + x) + (x ^ {2 } +1) = x ^ {3} + x ^ {2} + x + 1}
Умножение
Степень произведения полинома на ненулевой скаляр равна степени полинома; то есть
- deg (c P) = deg (P) { displaystyle deg (cP) = deg (P)}
.
Например, степень 2 (x 2 + 3 x — 2) = 2 x 2 + 6 x — 4 { displaystyle 2 (x ^ {2} + 3x-2) = 2x ^ {2} + 6x-4}

Таким образом, набор многочленов (с коэффициентами из заданного поле F), степени которого меньше или равны заданному числу n, образует векторное пространство ; для получения дополнительной информации см. Примеры векторных пространств.
В более общем смысле, степень произведения двух многочленов над полем или областью целостности является суммой их степеней :
- deg (PQ) = deg (P) + deg (Q) { displaystyle deg (PQ) = deg (P) + deg (Q)}
.
Например, степень из (x 3 + x) (x 2 + 1) = x 5 + 2 x 3 + x { displaystyle (x ^ {3} + x) (x ^ {2} +1) = x ^ { 5} + 2x ^ {3} + x}
Для многочленов над произвольным кольцом приведенные выше правила могут быть недействительными., из-за сокращения, которое может произойти при умножении двух ненулевых констант. Например, в кольце Z / 4 Z { displaystyle mathbf {Z} / 4 mathbf {Z}}


Состав
Степень композиции двух непостоянных многочленов P { displaystyle P}

- deg (P ∘ Q) = deg (P) deg (Q) { displaystyle deg (P circ Q) = deg (P) deg (Q)}
.
Например:
Обратите внимание, что для многочленов над произвольным кольцом это не обязательно верно. Например, в Z / 4 Z { displaystyle mathbf {Z} / 4 mathbf {Z}}


градус нулевого многочлена
Степень нулевого многочлена либо оставлена неопределенной, либо определена как отрицательная (обычно -1 или — ∞ { displaystyle — infty}
Как и любое постоянное значение, значение 0 можно рассматривать как (постоянный) многочлен, называемый нулевым многочленом . Он не имеет ненулевых членов, и поэтому, строго говоря, он также не имеет степени. Таким образом, его степень обычно не определена. Предложения для степени сумм и произведений многочленов в предыдущем разделе не применяются, если какой-либо из задействованных многочленов является нулевым многочленом.
Это удобно, однако, чтобы определить степень нулевого многочлена как отрицательную ive бесконечность, — ∞, { displaystyle — infty,}
- max (a, — ∞) = a, { displaystyle max (a, — infty) = a,}
и
- a + (- ∞) = — ∞. { displaystyle a + (- infty) = — infty.}
Эти примеры иллюстрируют, как это расширение удовлетворяет правилам поведения выше:
Вычисляется из значений функции
Ряд формул Существуют, которые будут оценивать степень полиномиальной функции f. Один, основанный на асимптотическом анализе, равен
- deg f = lim x → ∞ log | f (x) | log x { displaystyle deg f = lim _ {x rightarrow infty} { frac { log | f (x) |} { log x}}}
;
это точный аналог метод оценки наклона графика log – log.
Эта формула обобщает понятие степени на некоторые функции, не являющиеся полиномами. Например:
Формула также дает разумные результаты для многих комбинаций таких функций, например, степень 1 + xx { displaystyle { frac {1 + { sqrt {x}} } {x}}}

Другая формула для вычисления степени f по его значениям:
- deg f = lim x → ∞ xf ′ (x) f (x) { displaystyle deg f = lim _ {x to infty} { frac {xf ‘(x)} {f (x)}}}
;
эта вторая формула следует из применения правила Лопиталя к первой формуле. Интуитивно, однако, это больше связано с показом степени d как дополнительного постоянного множителя в производной dxd — 1 { displaystyle dx ^ {d-1}}

Более детальное (чем простая числовая степень) описание асимптотики функции может быть получено с помощью нотации большой буквы O. При анализе алгоритмов, например, часто бывает уместно различать темпы роста x { displaystyle x}

Расширение до многочленов с двумя или более переменными
Для многочленов от двух или более переменных степень члена — это сумма показателей степени переменных в члене; степень (иногда называемая общей степенью ) полинома снова является максимальной из степеней всех членов в полиноме. Например, многочлен xy + 3x + 4y имеет степень 4, ту же степень, что и член xy.
Однако многочлен от переменных x и y — это многочлен от x с коэффициентами, которые являются многочленами от y, а также многочлен от y с коэффициентами, которые являются многочленами от x. Многочлен
- x 2 y 2 + 3 x 3 + 4 y = (3) x 3 + (y 2) x 2 + (4 y) = (x 2) y 2 + (4) y + (3 x 3) { displaystyle x ^ {2} y ^ {2} + 3x ^ {3} + 4y = (3) x ^ {3} + (y ^ {2}) x ^ {2} + (4y) = (x ^ {2}) y ^ {2} + (4) y + (3x ^ {3})}
имеет степень 3 по x и степень 2 по y.
Функция степени в абстрактной алгебре
Дано кольцо R, кольцо многочленов R [x] — это множество всех многочленов от x, которые имеют коэффициенты в R. В частном случае, когда R также является полем, кольцо многочленов R [x] является областью главных идеалов и, что более важно для нашего обсуждения здесь, Евклидова область.
Можно показать, что степень полинома над полем удовлетворяет всем требованиям функции нормы в евклидовой области. То есть, учитывая два полинома f (x) и g (x), степень произведения f (x) g (x) должна быть больше, чем степени f и g по отдельности. На самом деле имеет место нечто более сильное:
- deg (f (x) g (x)) = deg (f (x)) + deg (g (x))
Пример того, почему функция степени может не работать. над кольцом, не являющимся полем, рассмотрим следующий пример. Пусть R = Z / 4 Z { displaystyle mathbb {Z} / 4 mathbb {Z}}
Поскольку функция нормы не определена для нулевого элемента кольца, мы считаем, что степень многочлена f (x) = 0 также не определена, так что она следует правилам нормы в евклидовом домен.
См. Также
Примечания
Ссылки
- Axler, Sheldon (1997), Linear Algebra Done Right (2-е изд.), Springer Science Business Media
- Чайлдс, Линдси Н. (1995), Конкретное введение в высшую алгебру (2-е изд.), Springer Science Business Media
- Чайлдс, Линдси Н. (2009), Конкретное введение в высшую алгебру (3-е изд.), Springer Science Business Media
- Грийе, Пьер Антуан (2007), Абстрактная алгебра (2-е изд.), Springer Science Business Media
- Кинг, Р. Брюс (2009), По ту сторону уравнения четверти, Springer Science Business Media
- Mac Lane, Saunders ; Биркофф, Гаррет (1999), Алгебра (3-е изд.), Американское математическое общество
- Шафаревич, Игорь Р. (2003), Дискурсы по алгебре, Springer Science Business Media
Внешние ссылки
10. Многочлены от одной переменной и действия над ними.
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например от переменной х.
По определению одночлена числа и буквы (в нашем случае одна буква — х) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида ахn, где а — некоторое число. Поэтому одночлен от одной переменной х — это выражение вида ахп, где а — некоторое число, п — целое неотрицательное число. Если а 0, то показатель степени п переменной х называется степенью одночлена. Например, 25х6 —одночлен шестой степени, — х2/3— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 0 = 0 • х = 0 • х2 = 0 • х3…).
По определению многочлен от одной переменной х — это сумма одночленов от одной переменной х (в которой приведены подобные слагаемые, то есть все одночлены-слагаемые имеют различную степень). Поэтому
Определение 1. Многочленом от одной переменной х называется выражение вида
f (х) = аnхn + аn-1 хn-1 + … + а2х2+а1х +а0, (1)
где коэффициенты аn, аn-1, …., а0 – некоторые числа.
Если аn 0, то этот многочлен называют многочленом п-й степени от переменной х. При этом член аnхп называют старшим членом многочлена f (х), число аn — коэффициентом при старшем члене, а член а0 — свободным членом. Например, 5х3 — 2х + 1 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена f (х) записывают так:
f (x) = b0xn + b1xn — 1 + … + b n — 1x + b n, где b0, b1, …, bn — некоторые числа.
Т е о р е м а 1. Одночлены ахn, где а ≠ 0, и bxm, где b ≠ 0, тождественно равны тогда и только тогда, когда а = b и п = т.д.
Одночлен ахn тождественно равен нулю тогда и только тогда, когда а = 0.
Поскольку равенство одночленов
aхn = bхn (2)
выполняется при всех значениях х (по условию эти одночлены тождественно равны), то, подставляя в это равенство х = 1, получаем, что a = b. Сокращая обе части равенства (2) на a (где a ≠ 0 по условию), получаем xn =xm . При х = 2 из этого равенства имеем: 2n = 2m. Поскольку 2n = 2• 2•… • 2 (n раз),
а 2m = 2 • 2 •… • 2 (m раз), то равенство 2n = 2m возможно только тогда, когда n = m.
Таким образом, из тождественного равенства axn = bxm (a 0, b 0) получаем, что a = b и n = m.
Если известно, что axn = 0 для всех х, то при х = 1 получаем a = 0. Поэтому одночлен axп тождественно равен нулю при a = 0 (тогда axn = 0 • xn = 0).
Далее любой одночлен вида 0 • хn будем заменять на 0.
Т е о р ем а 2. Если многочлен f (x) тождественно равен нулю (то
есть принимает нулевые значения при всех значениях х), то все
его коэффициенты равны нулю.
Для доказательства используем метод математической индукции.
Пусть f (x) = anхn + an-1хn-1 + … + a1х + a0 = 0 (тождественно).
При n = 0 имеем f (х) = a0 = 0, поэтому a0 = 0. То есть в этом случае утверждение теоремы выполняется.
Предположим, что при n = k это утверждение также выполняется: если многочлен akхk + ak-1хk-1 + … + a1х + a0 тождественно равен 0, то
ak = ak — 1 = … = a1 = a0 = 0.
Докажем, что данное утверждение выполняется и при n = k + 1. Пусть
f (x) = ak+1xk + akхk + … + a1х + a0 = 0. (3)
Поскольку равенство (3) выполняется при всех значениях х, то, подставляя в это равенство х = 0, получаем, что a0 = 0. Тогда равенство (3) обращается в следующее равенство: ak+1xk+1+ akxk + … + a1x = 0. Вынесем х в левой части этого равенства за скобки и получим
х (ak+1 + xk + akxk-1 + … + a1) = 0. (4)
Равенство (4) должно выполняться при всех значениях х. Для того чтобы оно выполнялось при х 0, должно выполняться тождество ak+1xk + akxk-1 + … + a1 = 0.
В левой части этого тождества стоит многочлен со степенями переменной от х0 до xk .Тогда по предположению индукции все его коэффициенты равны нулю: ak + 1 = ak = …= a1 = 0. Но мы также доказали, что a0 = 0,
поэтому наше утверждение выполняется и при n = k + 1. Таким образом, утверждение теоремы справедливо для любого целого неотрицательного n, то есть для всех многочленов.
Определение 2. Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 0 (х) или просто 0 (поскольку 0 (х) = 0).
Теорема 3. Если два многочлена f (x) и g (x) тождественно равны,
то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен f (х) = аnхn + аn-1хn — 1 + … + а2х2 + а1х + а0, а многочлен g (x) = bmxm + bm — 1xm — 1 + … + b2x2 + b1x + b0. Рассмотрим многочлен f (x) — g (x). Поскольку многочлены f (x) и g (x) по условию тождественно равны, то многочлен f (x) — g (x) тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Но f (x) — g (x) =(a0 — b0) + (a1 — b1) x +(а2 — b2) х2+ … .
Тогда a0 — b0 = 0, a1 — b1 = 0, а2 — b2 = 0, … . Отсюда a0 = b0, a1 = b1s а2 = b2, … . Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, n больше m), то коэффициенты разности будут равны нулю. Поэтому начиная с (m + 1)-го номера все коэффициенты at также будут равны нулю. То есть действительно многочлены f (x) и g (x) имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример. Докажите, что выражение (х + 2)(х + 4)(х + 6)(х + 
Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида ах2 + bх + с (а ≠ 0).
Получаем тождество:
(х + 2)(х + 4)(х + 6)(х + 8) + 16 = (ах2 + bх + с)2. (5)
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях х, получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
|
x4 |
1 = a2 |
|
x3 |
2 + 4 + 6 + 8 = 2ab |
|
x2 |
2-4 + 2-6 + 2-8 + 4-6 + 4-8 + 6-8 = b2 + 2ac |
|
x1 |
2-4-6 + 2-4-8 + 2-6-8 + 4-6-8 = 2bc |
|
x0 |
2 — 4 — 6 — 8 + 16 = c2 |
Из первого равенства получаем а = 1 или а = -1.
При а = 1 из второго равенства имеем b = 10, а из третьего — с = 20. Как видим, при этих значениях а, b и с последние два равенства также выполняются. Следовательно, тождество (5) выполняется при а = 1, b = 10, с = 20 (аналогично можно также получить а = -1, b = -10, с = -20).
Таким образом, (х + 2)(х+ 4)(х+ 6)(х+8) + 16=(х2 +10х + 20)2.
Упражнения
1. Зная, что многочлены f (x) и g (x) тождественно равны, найдите значение
коэффициентов а, b, с, d:
1)f (x) = 2x2 — (3 — а) x + b, g (x) = cx3 + 2dx2 + x + 5;
2)f (x) = (а + 1) x3 + 2, g (x) = 3x3 + bx2 + (c — 1) x + d.
2. Найдите такие числа a.b.c чтобы данное равенство a(x2-1)+b(x-2)+c(x+2)=2 выполнялось при любых значениях x.
3. Докажите тождество:
1)(x — 1)(х +1)(х2 — х + 1)(х2 + х +1) =х6 — 1;
2)1+х4=(1+х +х2)(1-х +х2).
4. Докажите, что данное выражение является полным квадратом:
1)(х — 1)(х — 2)(х — 3)(х — 4) + 1;
2)(х + а)(х + 2а)(х + 3а)(х + 4а) + а4.
5. Найдите такие а и b, чтобы при любых значениях х выполнялось равенство: 3х4 + 4х3 + 8х2 + 3х + 2 = (3х2 + ах + 1)(х2 + х + b).
6. Запишите алгебраическую дробь 2/15х2+x-2 как сумму двух алгебраических дробей вида a/3x-1 и b/5x+2
10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени можно получить многочлен этой же степени или многочлен меньшей степени.
Например, 2х3 — 5х2 + 3х + 1 + (-2х3 + 5х2 + х + 5) = 4х + 6.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей из степеней слагаемых.
Например, (3х3 — 5х + 7) + (х2 + 2х + 1) = 3х3 + х2 — 3х + 8.
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что число а делится на число b (b≠ 0), если существует такое число q, что а = b • q.
Определение 3. Многочлен А (х) делится на многочлен В (х) (где В (х) —не нулевой многочлен), если существует такой многочлен Q (x), что
А (х) = В (х) • Q (x).
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком
Разделить с остатком многочлен А (х) на многочлен В (х) (где В (х) — не нулевой многочлен) — это означает найти такую пару многочленов Q (x) и R (x), что А (х) = В (х) • Q (x) + R (x), причем степень остатка R (x) меньше степени делителя В (х) (в этом случае многочлен Q (х) называют неполным частным.)
Например, поскольку х3 — 5х + 2 = (х2 — 5) х + 2, то при делении многочлена х3 — 5х + 2 на многочлен х2 — 5 получаем неполное частное х и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом:
Алгоритм. При делении многочленов от одной переменной переменные в делимом и в делителе размещают по убыванию степеней и делят старший член делимого на старший член делителя. Потом полученный результат умножают на делитель, и это произведение вычитают из делимого. С полученной разностью выполняют аналогичную операцию: делят ее старший член на старший член делителя и полученный результат снова умножают на делитель и т. д. Этот процесс продолжают до тех пор, пока не получится в остатке 0 (если один многочлен делится на другой) или пока в остатке не получится многочлен, степень которого меньше степени делителя.
Пример. Разделим многочлен А (х) = х4 — 5х3 + х2 + 8х — 20 на многочлен B(x)= х2 — 2х+3
Докажем, что полученный результат действительно является результатом деления А (х) на В (х) с остатком.
Если обозначить результат выполнения первого шага алгоритма через f1 (x), второго шага — через f2 (x), третьего — через f3 (x), то операцию деления, выполненную выше, можно записать в виде системы равенств:
f1(x) = А (х) — х2 • В (х); (1)
f2 (x) = A (x) — (-3х) • В (х); (2)
f3 (x) = f2(x) — (-8) • В (х). (3)
Сложим почленно равенства (1), (2), (3) и получим
А (х) = (х2 — 3х — 
Учитывая, что степень многочлена f3 (x) = х + 4 меньше степени делителя
В (х) = х2 — 2х + 3, обозначим f3 (x) = R (x) (остаток), а х2 — 3х — 8 = Q (x) (неполное частное). Тогда из равенства (4) имеем: А (х) = В (х) — Q (x) + R (x), то есть х4 — 5х3 + х2 + 8х — 20 = (х2 — 2х + 3)(х2 — 3х — 
Очевидно, что приведенное обоснование можно провести для любой пары многочленов А (х) и В (х) в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого А (х) и делителя В (х) (где В (х) — не нулевой многочлен) найти неполное частное Q (x) и остаток R (x).
То есть, имеет место следующая теорема.
Теорема 4. Для любой пары многочленов А (х) и В (х) (где В (х) — не нулевой многочлен) существует и притом единственная пара многочленов
Q(x) и R(x), такая, что А(х)=В(х)*Q(x) + R(x), причем сте-
пень R (x) меньше степени В (х) (или R (x) — нулевой многочлен).
Отметим, что в случае, когда степень делимого А (х) меньше степени делителя В (х), считают, что неполное частное Q (x) = 0, а остаток R (x) = А (х).
Упражнения
1.Выполните деление многочлена на многочлен:
1)3х3 — 5х2 + 2х — 8 на х — 2; 2) х10 + 1 на х2 + 1;
3)х5 + 3х3 + 8х — 6 на х2 + 2х + 3.
2. Выполните деление многочлена на многочлен с остатком:
1)4х4 — 2х3 + х2 — х + 1 на x2 + x + 2;
2)х5 + х4 + х3 + х2 + 1 на х2 — х — 2.
3.При каких значениях а и b многочлен А (х) делится без остатка на многочлен В(х)?
1)А (х) = х3 + ах + b, В (х) = х2 + 5х + 7;
2)А (х) = 2х3 — 5х2 + ах + b, В (х) = х2 — 4;
3)А (х) = х4 — х3 + х2 — ах + b, В (х) = х2 — х + 2.
4.Найдите неполное частное и остаток при делении многочлена А(х) на многочлен В(х) методом неопределенных коэффициентов:
1)А (х) = х3 + 6х2 + 11х + 6, В (х) = х2 — 1;
2)А (х) = х3 — 19х — 30, В (х) = х2 + 1.
10.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА
Рассмотрим деление многочлена f (x) на двучлен (х – а). Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен f (x) на двучлен (х – а), то получим
f (x) = (х – а)*Q (x) + R.
Это равенство выполняется тождественно, то есть при любом значении х. При х = а имеем f (а) = R. Полученный результат называют теоремой Безу.
Те о р е м а 1 (теорема Безу). Остаток от деления многочлена f (х) на двучлен (х – а) равен f (а) (то есть значению многочлена при х = а).
Задача 1. Докажите, что х5 – 3х4 + 2х3 + 4х – 4 делится на х – 1 без остатка.
- Подставив в f (х) = х5 – 3х4 + 2х3 + 4х – 4 вместо х значение 1, получаем: f (1) = 0. Таким образом, остаток от деления f (х) на (х – 1) равен 0, то есть f (x) делится на (х – 1) без остатка.
О п р е д е л е н и е. Число α называют корнем многочлена f (x), если f (α) = 0.
Если многочлен f (х) делится на (х – α), то α — корень этого многочлена.
- Действительно, если f (х) делится на (х – α), то f (х) = (х – α)*Q (x) и поэтому f (α) = (α – α)*Q (α) = 0. Таким образом, α — корень многочлена f (х).
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Т е о р е м а 2. Если число α является корнем многочлена f (x), то этот многочлен делится на двучлен (х – α) без остатка.
- По теореме Безу остаток от деления f (x) на (х – α) равен f (α). Но по условию α — корень f (x), таким образом, f (α) = 0.
Обобщением теоремы 2 является следующее утверждение.
Те о р е м а 3. Если многочлен f (x) имеет попарно разные корни α1, α2, …, αn, то он делится без остатка на произведение
(х – α1)(x – α2)*…*(х – αn).
- Для доказательства используем метод математической индукции.
При n= 1 утверждение доказано в теореме 2. Допустим, что утверждение справедливо при n = k. То есть если α1, α2, …, αk — попарно разные корни многочлена f (x), то он делится на произведение (х – α1)(х – α2)*…*(х – αk). Тогда
f (x) = (х – α1)(х – α2)*…*(х – αk)*Q (x). (1)
Докажем, что утверждение теоремы справедливо и при n = k + 1. Пусть α1, α2, …, αk, αk + 1 — попарно разные корни многочлена f (x). Поскольку αk + 1 — корень f (x), то f (αk + 1) = 0.
Принимая во внимание равенство (1), которое выполняется согласно предположению индукции, получаем:
f (αk + 1) = (αk + 1 – α1)(αk + 1 – α2)*…*(αk + 1 – αk)*Q (αk + 1) = 0.
По условию все корни α1, α2, …, αk, αk + 1 разные, поэтому ни одно из чисел αk + 1 – α1, αk + 1 – α2, …, αk + 1 – αk не равно нулю. Тогда Q (αk + 1) = 0. Таким образом, αk + 1 — корень многочлена Q (x). Тогда по теореме 2 Q (x) делится на (х – αk + 1), то есть Q (x) = (х – αk + 1)*Q1 (x) и из равенства (1) имеем
f (x) = (х – α1)(х – α2)*…*(х – αk)(х – αk + 1)* Q1(x).
Это означает, что f (х) делится на произведение
(х – α1)(х – α2)*…*(х – αk)(х – αk + 1),
то есть теорема доказана и при n = k + 1.
Таким образом, теорема справедлива для любого натурального n.
С л е д с т в и е. Многочлен степени n имеет не больше n разных корней.
- Допустим, что многочлен n-й степени имеет (n + 1) разных корней: α1, α2, …, αn, αn+ 1. Тогда f (x) делится на произведение (х – α1)(х – α2)*… *(х – αn + 1) — многочлен степени (n+ 1), но это невозможно. Поэтому многочлен n-й степени не может иметь больше, чем n корней.
Пусть теперь многочлен n-й степени f (x) = аnхn + аn– 1 хn–1 + … + а2х2 + а1х + а0 (an ≠ 0) имеет n разных корней α1, α2, …, αn. Тогда этот многочлен делится без остатка на произведение (х – α1)(х – α2)*…*(х – αn). Это произведение является многочленом той же n-й степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 = b (х – α1)(х – α2)*…*(х – αn). (2)
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что b = аn, то есть
аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 = аn (х – α1)(х – α2)*…*(х – αn) (3)
Сравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
|
a1+a2+…+an= — an-1/an; |
a1a2+a1a3+…+an-1an= an-2/an; |
(4) |
|
a1a2a3+a1a2a4+…+an-2an-1an= — an-3/an; |
||
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
||
|
a1a2a3…an= (-1)n * a0/an. |
Например, при n = 2 имеем:
a1+a2= — a1/a2, a1a2 = a0/a2
а при n = 3:
| a1+a2+a3= — a2/a3; |
a1a2+ a1a3+ a2a3 = a1/a3; |
(5) |
|
a1a2a3 = — a0/a3. |
Выполнение таких равенств является необходимым и достаточным условием того, чтобы числа α1, α2, …, αn были корнями многочлена f (x) = аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 (an ≠ 0). Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена f (x) разные. Введем понятие кратного корня многочлена.
Если многочлен f (x) делится без остатка на (х – α)k, но не делится без остатка на (х – α)k + 1, то говорят, что число α является корнем кратности k многочлена f (x).
Например, если произведение (х + 2)3(х – 1)2(х + 3) записать в виде многочлена, то для этого многочлена число (–2) является корнем кратности 3, число 1 — корнем кратности 2, а число (–3) — корнем кратности 1.
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Задача 2. Проверьте справедливость формул Виета для многочлена
f (x) = х3 + 2х2 – 4х – 8.
- f(x) = х3 + 2х2 – 4х – 8 = х2 (х + 2) – 4 (х + 2) = (х + 2)(х2 – 4) = (х – 2)(х + 2)2 .
Поэтому f (х) имеет корни: α1 = 2, α2 = –2, α3 = –2 (поскольку (–2) — корень кратности 2). Проверим справедливость формулы (5).
В нашем случае: а3 = 1, а2 = 2, а1= –4, а0 = –8. Тогда
2+(-2)+(-2)=-2/1; 2*(-2)+2*(-2)+(-2)*(-2)=-4/1; 2*(-2)*(-2)=-(-8)/1
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Задача 3. Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения х2 – 8х + 4 = 0.
- Обозначим корни уравнения х2 – 8х + 4 = 0 через х1 и х2. Тогда корнями искомого уравнения должны быть числа a1=x12 и a2=x22 . Поэтому искомое уравнение имеет вид х2 + рх + q = 0,
где p=-(a1+a2)=-(x12+x22)=-((x1+x2)2-2x1x2), q=a1a2=x12x22=(x1x2)2
По формулам Виета имеем х1 + х2 = 8 и х1х2 = 4. Отсюда находим, что
q = (х1х2)2 = 42 = 16, а p = −((x1+x2)2-2x1x2) = -(82-2*4)=-56.
Таким образом, искомое уравнение имеет вид х2 – 56х + 16 = 0.
Упражнения
- Найдите остаток от деления многочлена х5 – 4х4 + 2х3 – 5х + 1 на х + 2.
- Найдите коэффициент а, зная, что остаток от деления многочлена х3 – ах2 + 5х – 3 на х – 1 равен 6.
- Многочлен f (х) при делении на х – 1 дает остаток 4, а при делении на х – 3 дает остаток 6. Найдите остаток от деления многочлена f (х) на х2 – 4х + 3.
- При каких значениях а и b многочлен х4 + 2х3 + ах2 – bх + 2 делится без остатка на х + 2, а при делении на х – 1 имеет остаток, который равен 3?
- Остаток от деления многочлена f (x) на 3х2 – 5х + 2 равен 7х + 1. Найдите остаток от деления этого многочлена на двучлены х – 1 и 3х – 2.
- Запишите формулы Виета при n = 4.
- Составьте кубический многочлен, который имеет корни 5, –2, 1 и коэффициент при старшем члене –2. Решите задачу двумя способами.
- При каких значениях а сумма квадратов корней трехчлена х2 – (а + 2) х + 3а равна 12?
- Какую кратность имеет корень 2 для многочлена
f (х) = х5 – 5х4 + 7х3 – 2х2 + 4х – 8?
- Составьте кубический многочлен, который имеет корень 3 кратности 2 и корень (–1), а коэффициент при старшем члене 2.
- Найдите такие а и b, чтобы число 3 было корнем кратности не меньше чем 2 для многочлена f (х) = х3 – 5х2 + ах + b.
- Составьте квадратное уравнение, корни которого противоположны корням уравнения х2 – 5х + 1 = 0.
- Составьте квадратное уравнение, корни которого обратны корням уравнения 2х2 – 5х + 1 = 0.
- Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения х2 + 6х + 3 = 0.
10.4. СХЕМА ГОРНЕРА
Делить многочлен f (x) на двучлен (х – а) иногда удобно с помощью специальной схемы, которую называют схемой Горнера.
- Пусть многочлен f (x) = а0хn + а1хn– 1 + … + аn – 1 х + аn (a0 ≠ 0) необходимо разделить на двучлен (х – а). В результате деления многочлена n-й степени на многочлен первой степени получим некоторый многочлен Q (x) (n – 1)-й степени (то есть Q (x) = b0x n – 1 + b1x n – 2 + … + bn – 2 x + b n – 1, где b0 ≠ 0) и остаток R. Тогда f (x) = (х – а)*Q (x) + R, то есть а0хn + а1хn – 1 + … + аn – 1 х + аn = = (х – а)*(b0xn – 1 + b1xn – 2 + … + bn – 2 x + bn – 1) + R. Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях х:
Xn
а0 = b0
Xn-1
а1 = b1 – аb0
Xn-2
а2 = b2 – аb1
. . . . . .
. . . . . . . . . . . .
X1
аn – 1 = bn – 1 – аbn – 2
X0
аn = R – аbn – 1
Найдем из этих равенств коэффициенты b0, b1, …, bn – 1 и остаток R: b0 = а0, b1 = ab0 + a1, b2 = ab1 + a2, …, bn – 1 = abn – 2 + an – 1, R = abn – 1 + an.
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент bk + 1 неполного частного, достаточно предыдущий найденный коэффициент bk умножить на а и добавить k-й коэффициент делимого. Эту процедуру целесобразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.
Пример 1. Разделите по схеме Горнера многочлен f (х) = 3х4 – 2х3 – 4х + 1 на двучлен х – 2.
Запишем сначала все коэффициенты многочлена f (х) (если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:
Таким образом, 3х4 – 2х3 – 4х +1 = (х – 2)(3х3 + 4х2 + 8х + 12) + 25.
Пример 2. Проверьте, является ли х = –3 корнем многочлена f (х) = 2х4 + 6х3 + 4х2 – 2х – 42.
- По теореме Безу остаток от деления многочлена f (х) на х – а равен f (а), поэтому найдем с помощью схемы Горнера остаток от деления f (х) на х – (–3) = х + 3
Поскольку f (–3) = 0, то х = –3 — корень многочлена f (х).
Упражнения
- Используя схему Горнера, найдите неполное частное и остаток от деления многочлена А (х) на двучлен В (х):
1) А (х) = х3 + 3х2 + 3х + 1; В (х) = х + 1;
2) А (х) = 5х3 – 26х2 + 25х – 4; В (х) = х – 5;
3) А (х) = х4 – 15х2 + 10х + 24; В (х) = х + 3.
- Используя схему Горнера, проверьте, делится ли многочлен f (x) на двучлен q (x):
1) f (х) = 4х3 – х2 – 27х – 18; q (x) = x + 2;
2) f (х) = х4 – 8х3 + 15х2 + 4х – 20; q (x) = x – 2.
- Разделите многочлен А (х) на двучлен В (х):
1) А (х) = 2х3 – 19х2 + 32х + 21; В (х) = х – 7;
2) А (х) = 4х3 – 24х2 + 21х – 5; В (х) = 2х – 1.
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ.
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.
Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
|
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0. |
(1) |
Умножим обе части равенства (1) на (q ≠ 0). Получаем
|
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0. |
(2) |
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.
Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
|
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d), |
(3) |
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
х4 + х3 + 3х2 + х + 6 = x4 + cx3 + dx2 +
+ ax3 + acx2 + adx +
+ bx2 + bcx + bd.
Получаем систему
 |
(4) |
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
|
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3). |
(5) |
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.
- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х2 + bх + с)2 – (mх + n)2: :
1) х4+ 4х – 1;
2) х4 – 4х3 – 1;
3) х4 + 4а3х – а4.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1
- Область определения функции y = f (x) ¾ отрезок [– 2; 1]. Найдите область определения функции:
- Постройте график функции:
- Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют заданному условию:
4 (МТУСИ). Решите уравнение:
5 (МЭСИ). Решите систему уравнений:
- Решите неравенство:
- Докажите неравенство:
8 (СТАНКИН). Найдите все значения параметра а, при которых уравнение имеет точно три корня.
9 (МГАТХТ). Найдите все значения параметра а, при которых система уравнений не имеет решений.
10 (МГУ, ИСАиА). Найдите все значения параметра а, при которых система уравнений имеет единственное решение.
11 (МИСиС). При каких значениях параметра а неравенство
выполняется для всех отрицательных значений х?
12 (МГУ, мех.-мат. ф-т). При каких значениях параметра а уравнение
имеет точно три различных корня?
- При каких значениях параметра а уравнение
имеет три действительных корня, которые образуют геометрическую прогрессию?
Решите задачи (14–25) на составление уравнений или неравенств и их систем.
14 (МГТУ). Рабочий должен был по плану изготовить за несколько дней 72 детали. Так как каждый день он изготавливал на 2 детали меньше плана, то закончил работу через 3 дня после срока. Сколько деталей в день должен был изготовлять рабочий по плану?
15 (МГУ, хим. ф-т). Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле (другой площади). Вся работа заняла 12 часов. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал один из них, то работа заняла бы 20 часов. За какое время два комбайна могут убрать первое поле?
16 (РЭА). Производительность первого станка на 25 % больше производительности второго станка. Второй станок сделал деталей на 4 % больше, чем первый. На сколько процентов время, затраченное вторым станком на выполнение своей работы, больше времени первого станка?
17 (ГФА). Первая из труб наполняет бассейн водой в два раза быстрее, чем другая. Если половину бассейна наполнить только из первой трубы, а оставшуюся часть — только из второй, то для наполнения бассейна потребуется 6 час. За сколько часов можно наполнить бассейн только из первой трубы?
18 (МГУПБ). Два велосипедиста выезжают одновременно навстречу друг другу из пунктов А и В, расстояние между которыми 30 км, и встречаются через час. Не останавливаясь, они продолжают путь с той же скоростью, и первый прибывает в пункт В на 1,5 часа раньше, чем второй в пункт А. Определить скорость первого велосипедиста.
19 (МГУПБ). В течение 7 ч 20 мин судно прошло вверх по реке 35 км и вернулось обратно. Скорость течения равна 4 км в час. С какой скоростью судно шло по течению?
20 (ПГУ). Смешали 30 %-ный раствор соляной кислоты с 10 %-ным и получили 600 г 15 %-го раствора. Сколько граммов каждого раствора было взято?
21 (ВШЭ). Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40 % олова, а второй — 26 % меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30 % цинка. Определить, сколько килограммов олова содержится в новом сплаве.
22 (МАИ). Найти такое двузначное число, в котором число его единиц на два больше числа десятков, а произведение искомого числа на сумму его цифр равно 144.
23 (ЛТА). Около дома посажены березы и липы, причем общее их количество более 14. Если количество лип увеличить вдвое, а количество берез увеличить на 18, то берез станет больше. Если увеличить вдвое количество берез, не изменяя количества лип, то лип все равно будет больше. Сколько берез и сколько лип было посажено?
24 (МГУ, эк. ф-т, ВШЭ). Группу людей пытались построить в колонну по 8 человек в ряд, но один ряд оказался неполным. Когда ту же группу людей перестроили по 7 человек в ряд, то все ряды оказались полными, а число рядов оказалось на 2 больше. Если бы тех же людей построили по 5 человек в ряд, то рядов было бы еще на 7 больше, причем один ряд был бы неполным. Сколько людей было в группе?
25 (МГУ, эк. ф-т). В магазине продаются гвоздики и розы. Гвоздика стоит 1 руб. 50 коп., роза — 2 руб. На покупку гвоздик и роз можно затратить не более 30 руб. 50 коп. При этом число гвоздик не должно отличаться от числа роз более чем на 6. Необходимо купить максимально возможное суммарное количество цветов, при этом гвоздик нужно купить как можно меньше. Сколько гвоздик и сколько роз будет куплено при указанных условиях?















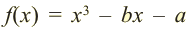
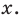
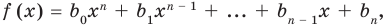
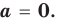
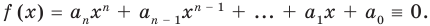
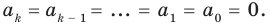
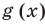
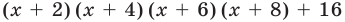
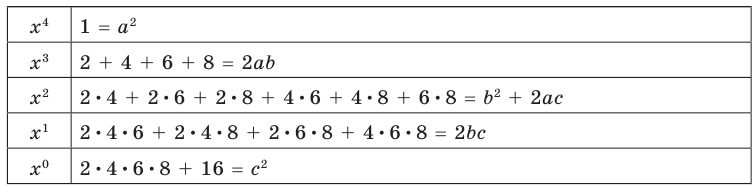
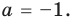
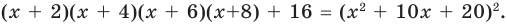
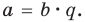
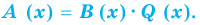
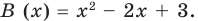
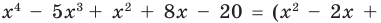
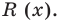
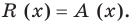
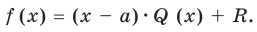
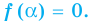
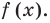
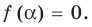
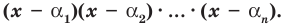
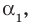
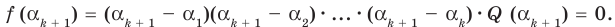

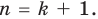
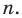
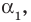
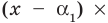
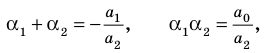
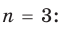
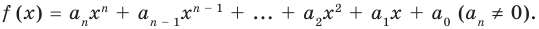
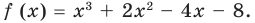
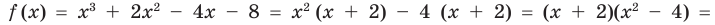
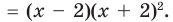
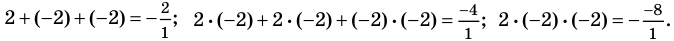
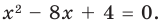
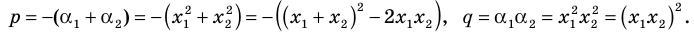
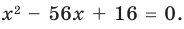
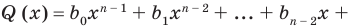
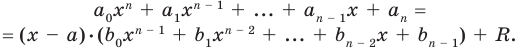
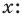
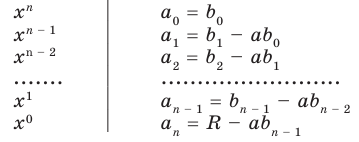



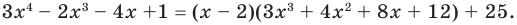
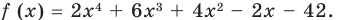
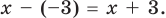

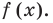
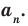
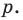
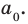
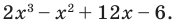
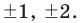
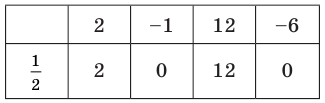
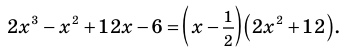
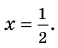
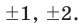
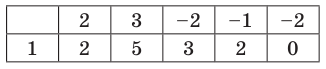
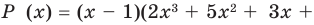
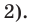

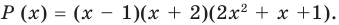
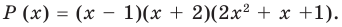
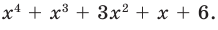
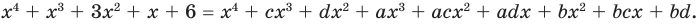
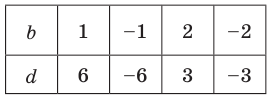

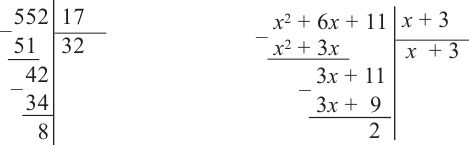
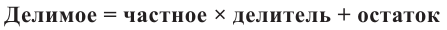
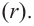
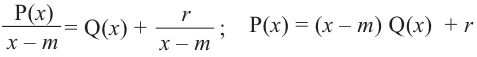
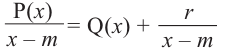
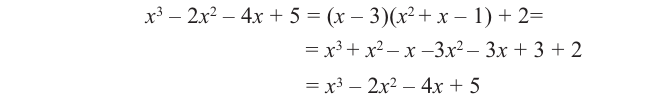
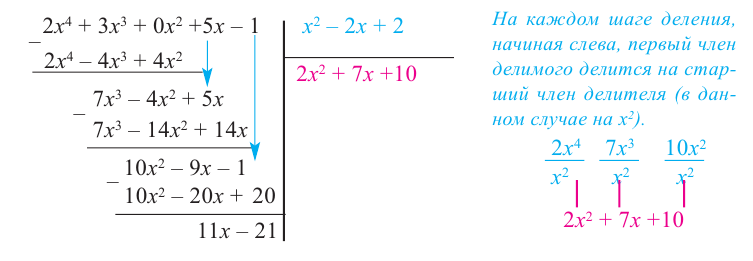
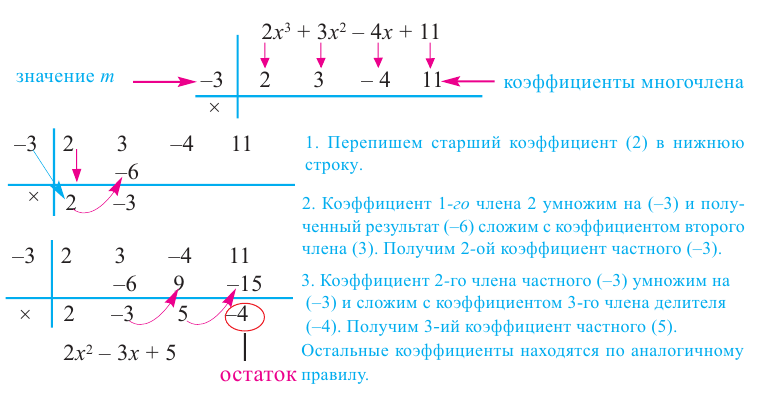
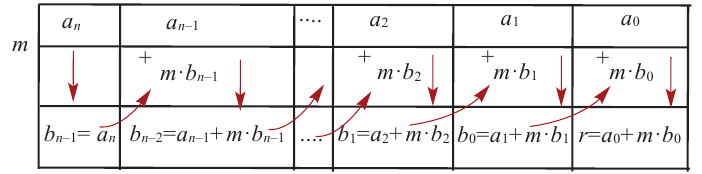
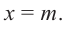
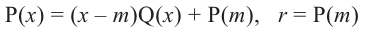
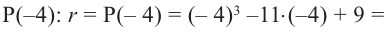
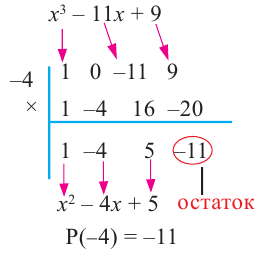
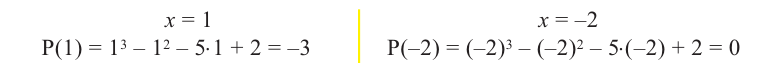
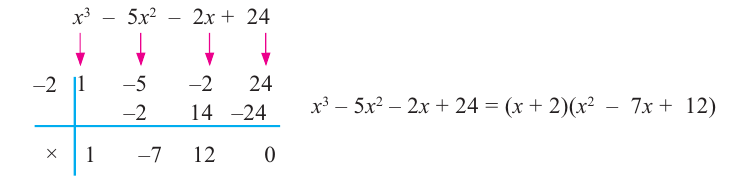
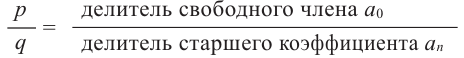
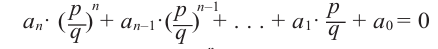
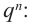
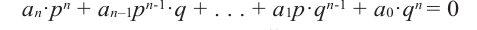
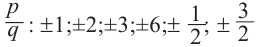
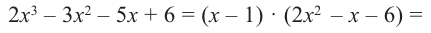
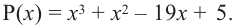
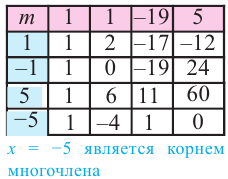
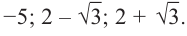
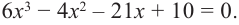
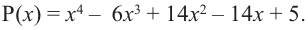
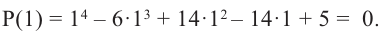
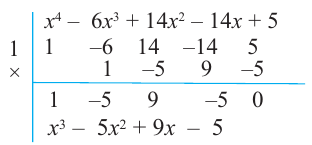
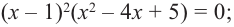
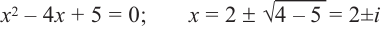
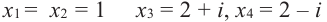
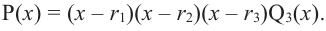
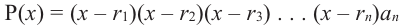
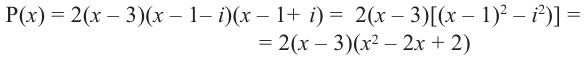
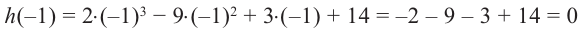
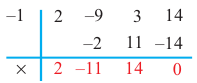
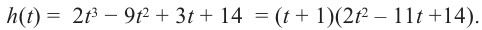
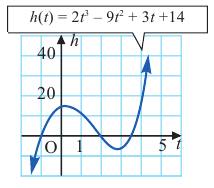
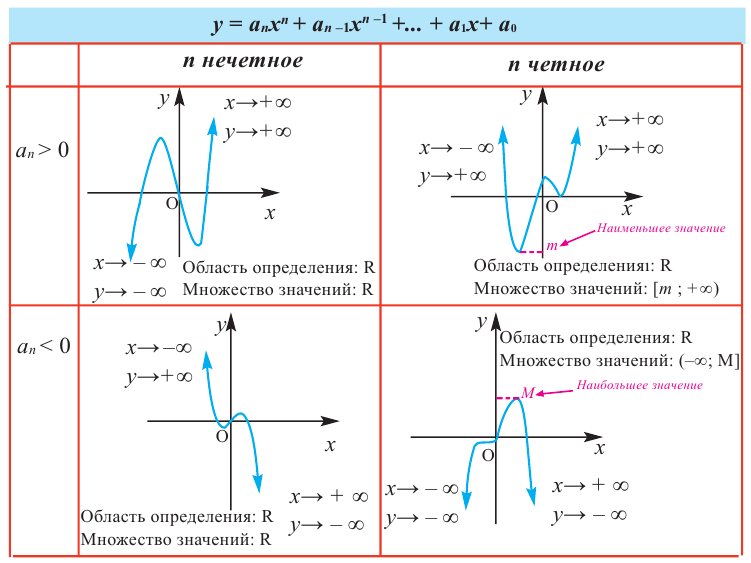
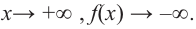
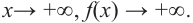
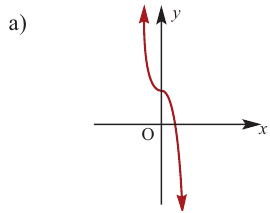
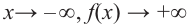
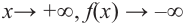
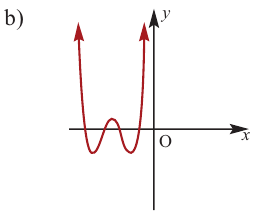
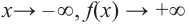
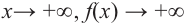
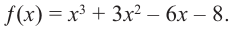
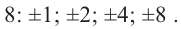
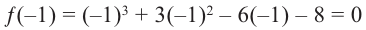
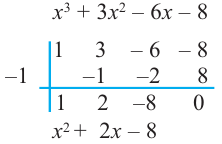
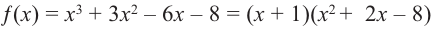
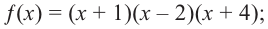
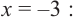
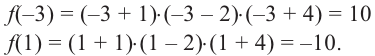
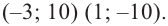
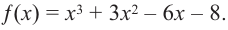
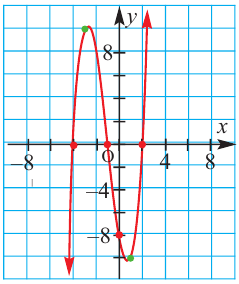
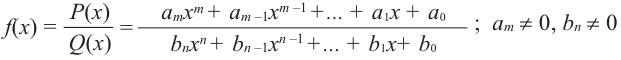
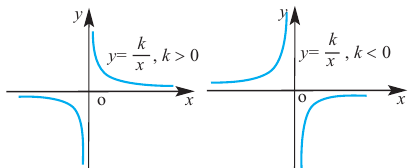
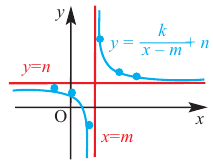
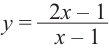
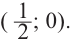
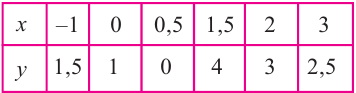
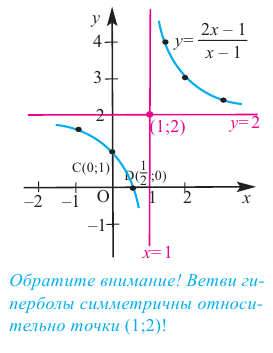
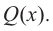
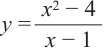
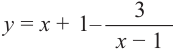
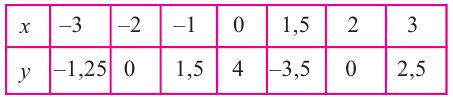
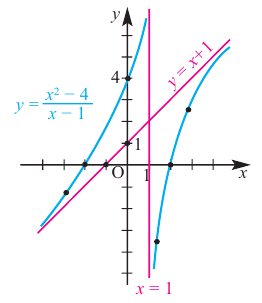
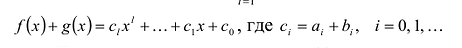
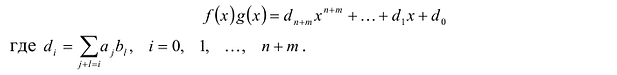
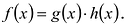
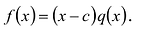
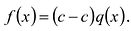

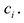
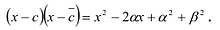
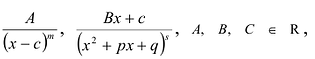
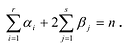
 .
..jpg)














