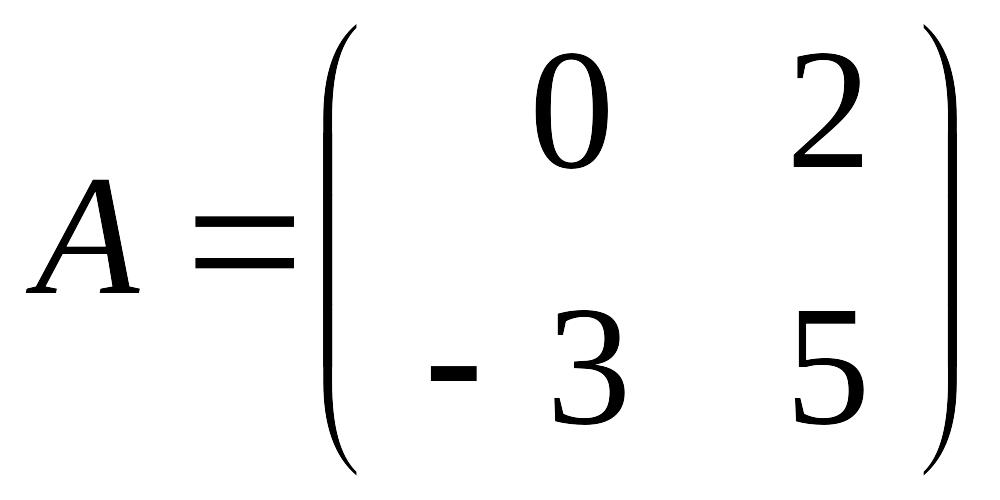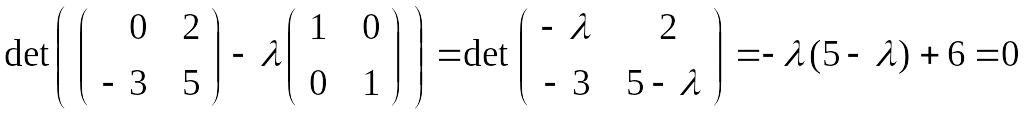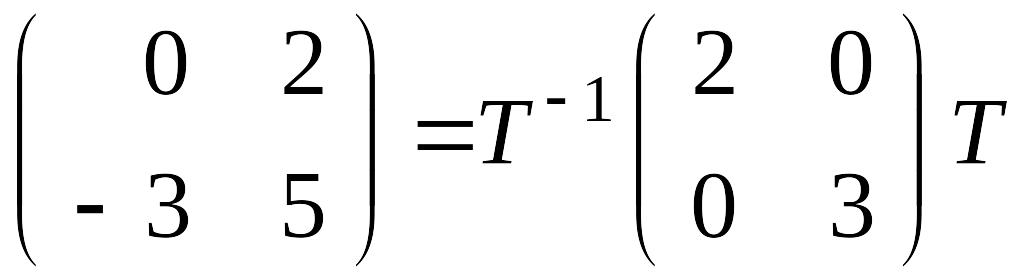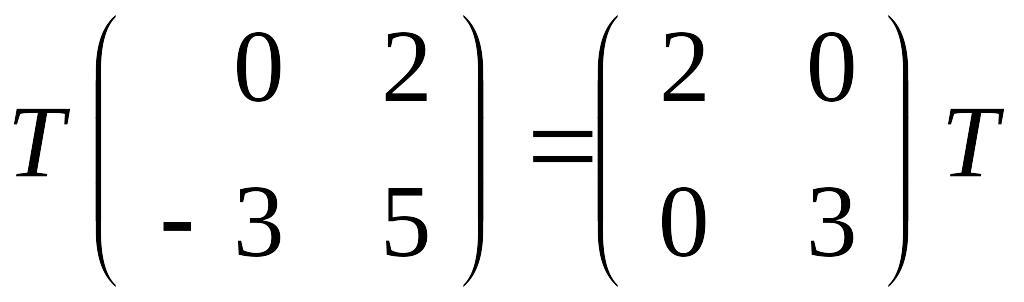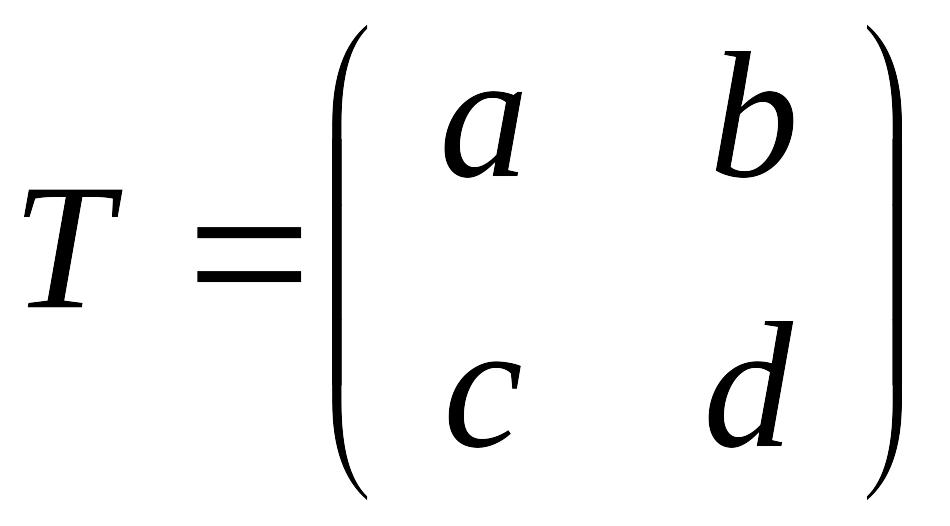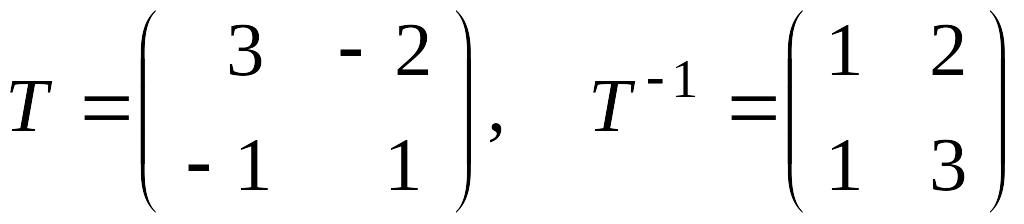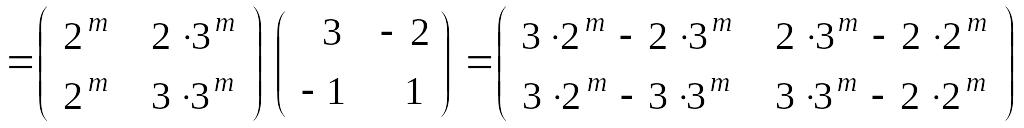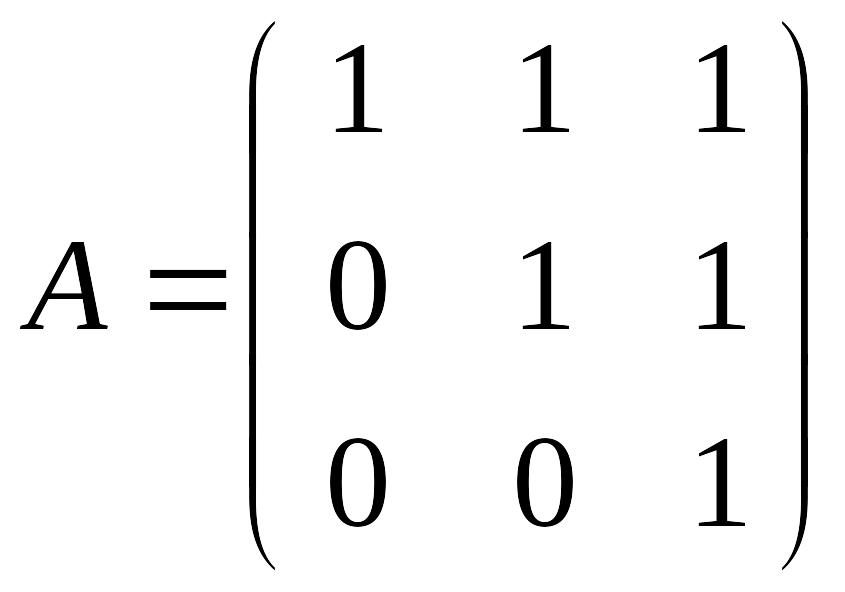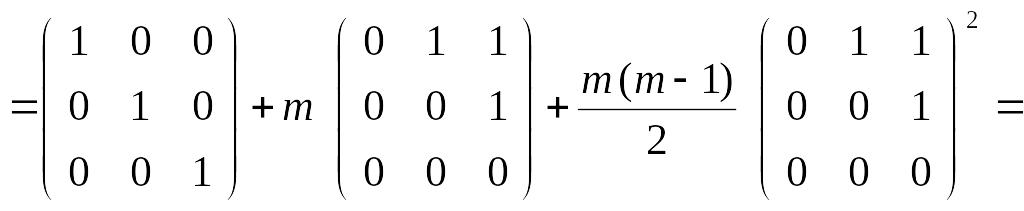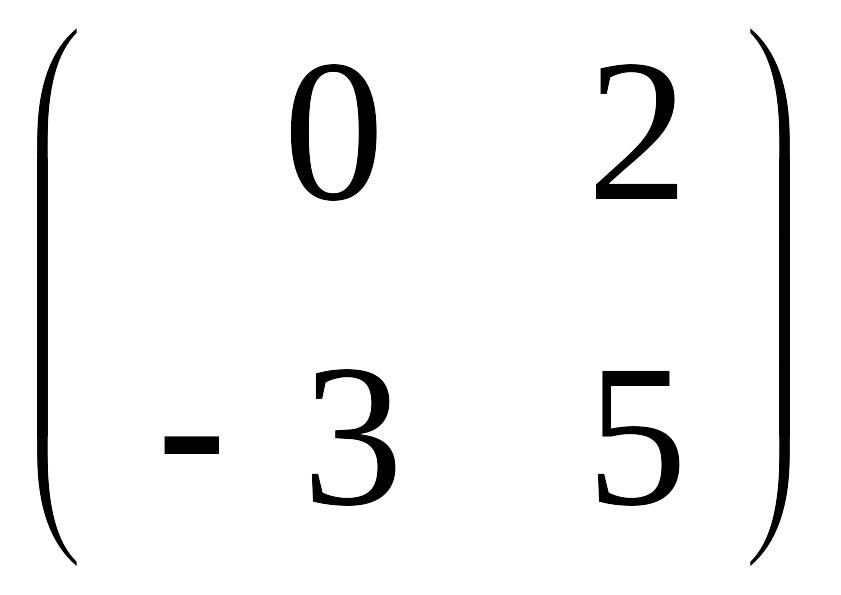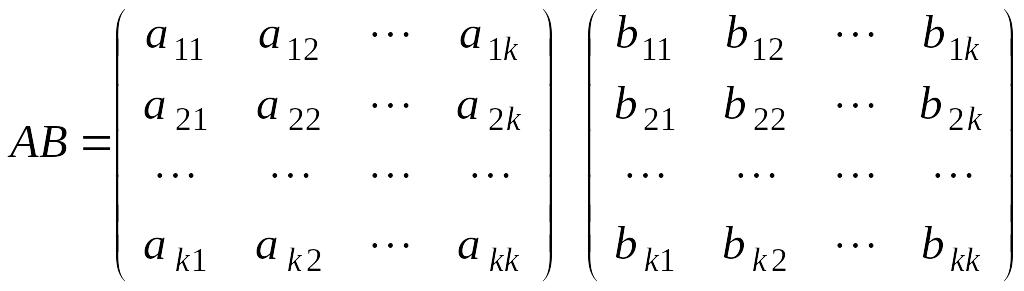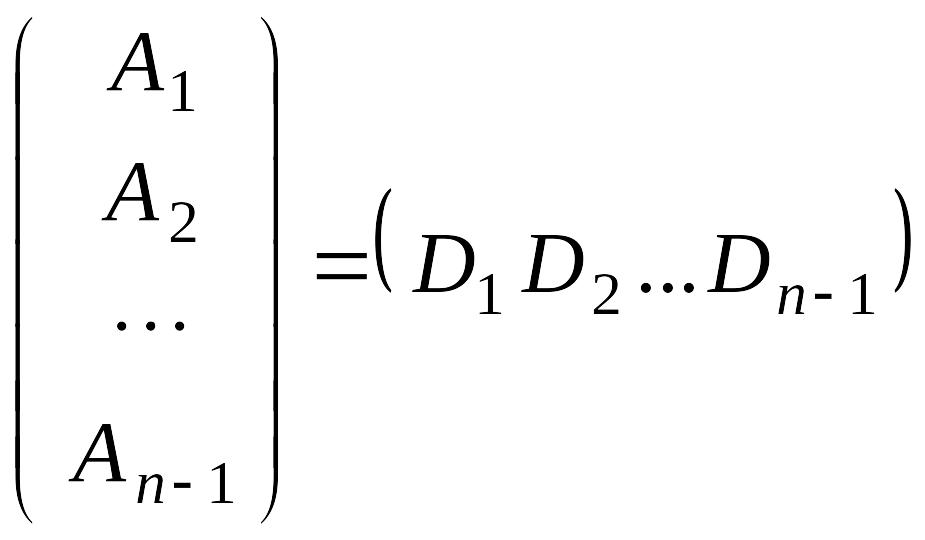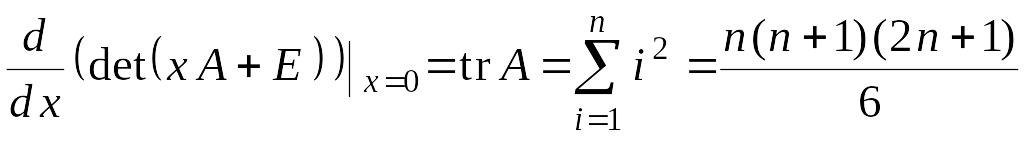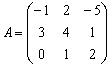Как найти степени матриц - Исправление недочетов и поиск решений вместе с Examum.ru

Мы уже знакомы с понятием матрицы, с основными действиями над ней. Перед тем, как начать изучение новой темы необходимо вспомнить операцию умножения матриц. В процессе изучения темы нами будет рассмотрен новый материал и отработаны действия над матрицами. Приступим к рассмотрению темы.

Операция возведения в степень kk определена только для квадратных матриц, т.е. матриц размера k×kktimes k (матриц kk-го порядка) — 2×22times 2, 3×33times 3 и т.д. Кроме того, показатель степени (число в которое мы возводим матрицу) должен быть натуральным: 1,2,3,4,5,…1, 2, 3, 4, 5, …

Онлайн-калькулятор

Возведение матрицы в степень

Для того чтобы возвести матрицу AA в степень kk, необходимо умножить матрицу AA саму на себя kk раз: Ak=A⋅A⋅…⋅AA^{k}=Acdot Acdot…cdot A.

Таким образом,

A2=A⋅AA^{2}=Acdot A,

A3=A⋅A⋅AA^{3}=Acdot Acdot A,

A4=A⋅A⋅A⋅AA^{4}=Acdot Acdot Acdot A и т.д.

Для степеней матрицы справедливо следующее свойство: At⋅Af=At+fA^{t}cdot A^{f}=A^{t+f}.

Пример 1

Найти A3A^{3} для матрицы A=(25171011)A=begin{pmatrix}25&17\10&11end{pmatrix}.

По свойству степеней: A3=A2⋅AA^{3}=A^{2}cdot A.

A2=A⋅A=(25171011)⋅(25171011)=A^{2}=Acdot A=begin{pmatrix}25&17\10&11end{pmatrix}cdot begin{pmatrix}25&17\10&11end{pmatrix}=

=(25⋅25+17⋅1025⋅17+17⋅1110⋅25+11⋅1010⋅17+11⋅11)=(795612360291)=begin{pmatrix}25cdot25+17cdot10&25cdot17+17cdot11\10cdot25+11cdot10&10cdot17+11cdot11end{pmatrix}=begin{pmatrix}795&612\360&291end{pmatrix}.

A3=A2⋅A=(795612360291)⋅(25171011)=A^{3}=A^{2}cdot A=begin{pmatrix}795&612\360&291end{pmatrix}cdot begin{pmatrix}25&17\10&11end{pmatrix}=

=(795⋅25+612⋅10795⋅17+612⋅11360⋅25+291⋅10360⋅17+291⋅11)=(2599520247119109321)=begin{pmatrix}795cdot25+612cdot10&795cdot17+612cdot11\360cdot25+291cdot10&360cdot17+291cdot11end{pmatrix}=begin{pmatrix}25995&20247\11910&9321end{pmatrix}.

Значит, A3=(2599520247119109321)A^{3}=begin{pmatrix}25995&20247\11910&9321end{pmatrix}.

Пример 2

Найти B4B^{4} для матрицы B=(573418962)B=begin{pmatrix}5&7&3\4&1&8\9&6&2end{pmatrix}.

По свойству степеней: B4=B2⋅B2B^{4}=B^{2}cdot B^{2}.

B2=B⋅B=(573418962)⋅(573418962)=B^{2}=Bcdot B=begin{pmatrix}5&7&3\4&1&8\9&6&2end{pmatrix}cdot begin{pmatrix}5&7&3\4&1&8\9&6&2end{pmatrix}=

=(5⋅5+7⋅4+3⋅95⋅7+7⋅1+3⋅65⋅3+7⋅8+3⋅24⋅5+1⋅4+8⋅94⋅7+1⋅1+8⋅64⋅3+1⋅8+8⋅29⋅5+6⋅4+2⋅99⋅7+6⋅1+2⋅69⋅3+6⋅8+2⋅2)=(806077967736878179)begin{pmatrix}5cdot5+7cdot4+3cdot9&5cdot7+7cdot1+3cdot6&5cdot3+7cdot8+3cdot2\4cdot5+1cdot4+8cdot9&4cdot7+1cdot1+8cdot6&4cdot3+1cdot8+8cdot2\9cdot5+6cdot4+2cdot9&9cdot7+6cdot1+2cdot6&9cdot3+6cdot8+2cdot2end{pmatrix}=begin{pmatrix}80&60&77\96&77&36\87&81&79end{pmatrix}.

B4=B2⋅B2=(806077967736878179)⋅(806077967736878179)=B^{4}=B^{2}cdot B^{2}=begin{pmatrix}80&60&77\96&77&36\87&81&79end{pmatrix}cdot begin{pmatrix}80&60&77\96&77&36\87&81&79end{pmatrix}=

=(80⋅80+60⋅96+77⋅8780⋅60+60⋅77+77⋅8180⋅77+60⋅36+77⋅7996⋅80+77⋅96+36⋅8796⋅60+77⋅77+36⋅8196⋅77+77⋅36+36⋅7987⋅80+81⋅96+79⋅8787⋅60+81⋅77+79⋅8187⋅77+81⋅36+79⋅79)==begin{pmatrix}80cdot80+60cdot96+77cdot87&80cdot60+60cdot77+77cdot81&80cdot77+60cdot36+77cdot79\96cdot80+77cdot96+36cdot87&96cdot60+77cdot77+36cdot81&96cdot77+77cdot36+36cdot79\87cdot80+81cdot96+79cdot87&87cdot60+81cdot77+79cdot81&87cdot77+81cdot36+79cdot79end{pmatrix}=

=(188591565714403182041460513008216091785615856)=begin{pmatrix}18859&15657&14403\18204&14605&13008\21609&17856&15856end{pmatrix}.

Значит, B4=(188591565714403182041460513008216091785615856)B^{4}=begin{pmatrix}18859&15657&14403\18204&14605&13008\21609&17856&15856end{pmatrix}.

На сервисе Студворк вы можете заказать помощь с выполнением контрольной по любому предмету!

Источник

В начале этого
раздела рассмотрим различные способы
возведения матрицы в степень.

Первый способ
основан на представлении матрицы А в
виде

,
где J – жорданова
форма А, и на использовании формулы

и формулы для

из упражнения 5 предыдущего раздела.

Упражнение
1. Вычислить

,
где

.

Решение.
Найдем собственные значения матрицы
А, т.е. решения уравнения

Отсюда

.
По теореме Жордана найдется матрица Т
такая, что выполнено равенство

,
или, что то же самое,

.
Определим матрицу Т. Пусть

.
Тогда матричное уравнение

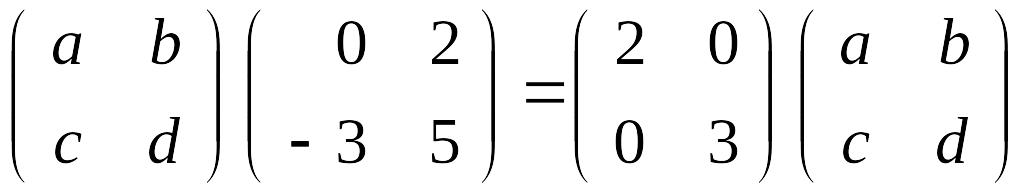
приводит к системе

одним из решений которой будет

Отсюда

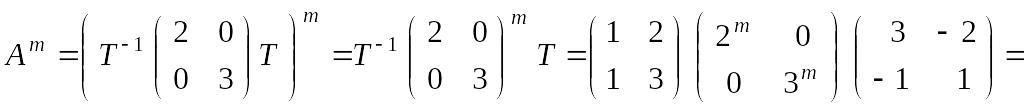
Второй
способ. Индуктивный метод вычисления

.
Этот метод основан на вычислении
нескольких первых степеней матрицы А,
установлении закономерностей изменения
элементов

и строгом доказательстве методом
математической индукции.

Упражнение
2. Вычислить

,
где

.

Решение.
Для начала вычислим

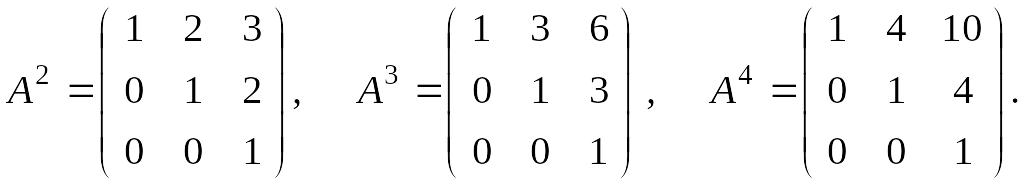
Заметим, что
элементы главной диагонали равны 1.
Элементы над главной диагональю совпадают
со степенью матрицы А, а для элемента

матрицы

при m = 2, 3, 4 выполнено
равенство

Теперь мы можем
сделать индуктивное предположение

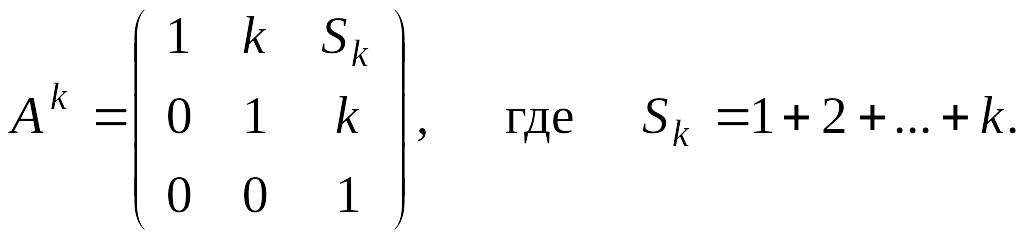
Покажем, что

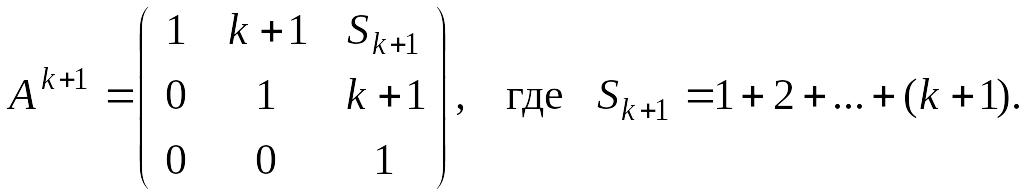
Действительно,

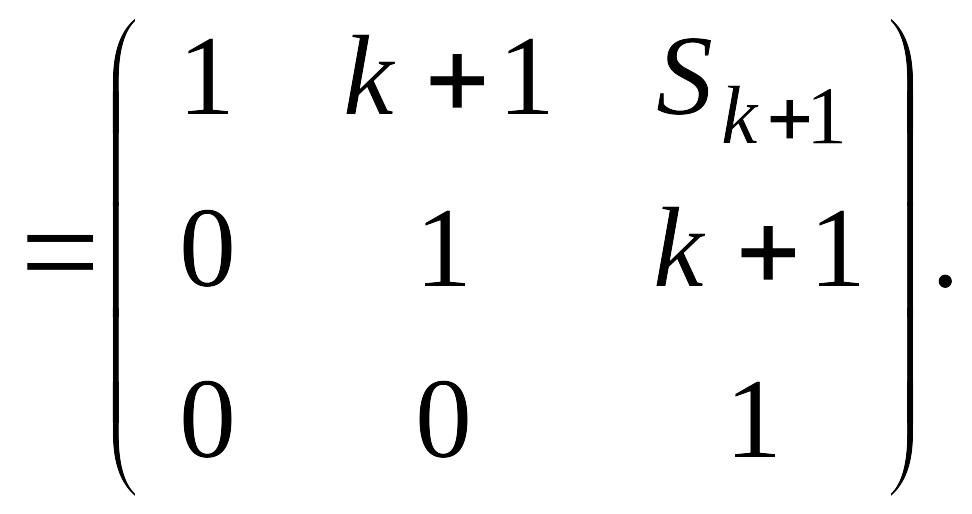
Что
и требовалось доказать. Это означает,
что

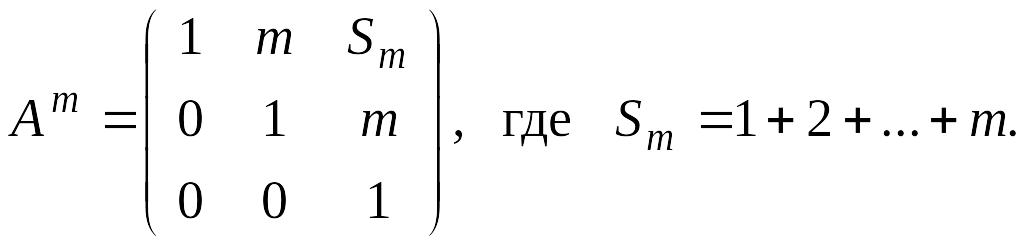
Третий
способ основан на применении
матричного аналога формулы бинома
Ньютона.

Теорема
1. Если матрицы А и В перестановочны
(то есть выполнено равенство АВ =
ВА), то

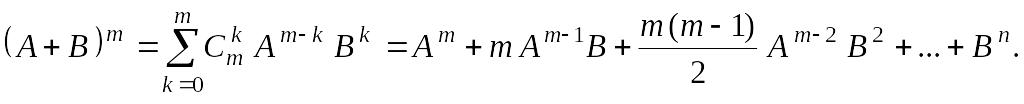
Если матрица
B в условии теоремы 1
нильпотентна (то есть

для не-которого

),
то для всех

верна формула

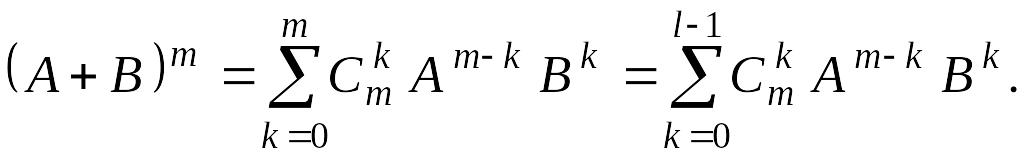
Фактически мы
уже пользовались этим результатом при
нахождении степеней жордановой клетки

при решении упражнения 5.

Применим
формулу бинома Ньютона для решения
упражнения 2 раздела 1.5. Запишем А в
виде суммы перестановочных матриц:

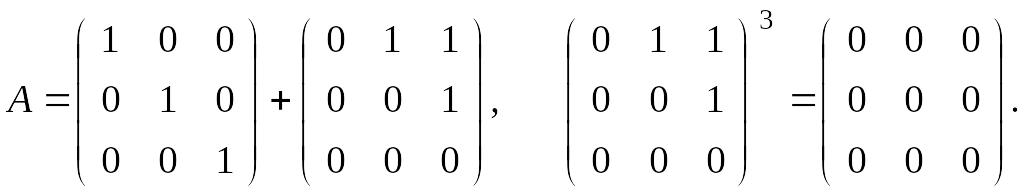
Таким
образом, для

получаем

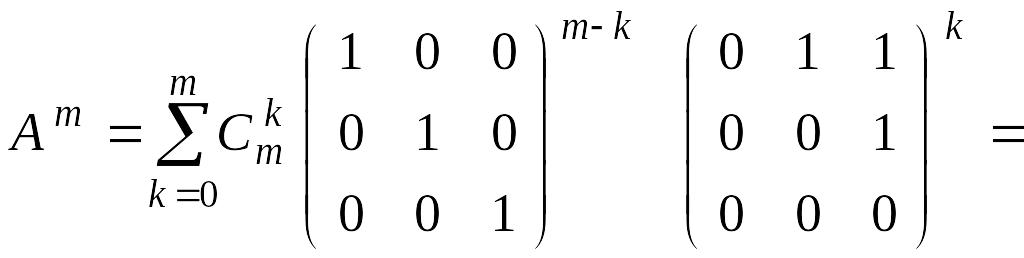
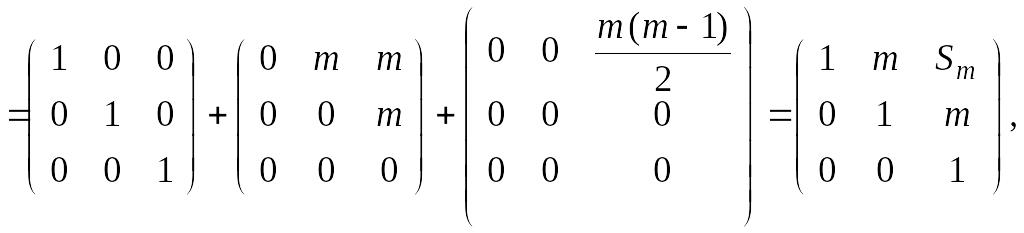
где

согласно формуле суммы m
первых членов арифметической прогрессии
1, 2, 3, … .

Для
m = 2 матрица

вычисляется непосредственно.

Замечание.
Отметим, что использование первого
способа не всегда оправдано для матриц
больших размерностей, так как для
вычисления элементов матрицы T
уже при n = 4 требуется
решать систему из 16 уравнений. С другой
стороны, применение второго и третьего
способов затруднительно для вычисления
степеней простейших матриц второго
порядка типа

(предлагаем читателям проверить это
самостоятельно).

Определение
1.
Следом квадратной матрицы А
назы-вается сумма элементов главной
диагонали и обозначается
.

Лемма..
Пусть А и В – квадратные матрицы
порядка n. Тогда
выполнено равенство

.

Доказательство.
Используем метод математической
индукции.

1.
Для n = 2 утверждение
проверяется непосредственно.

2.
Предположим, что утверждение верно для
некоторого

.

3.
Покажем, что оно верно для

.

Обозначим
строки и столбцы матриц

следующим образом:

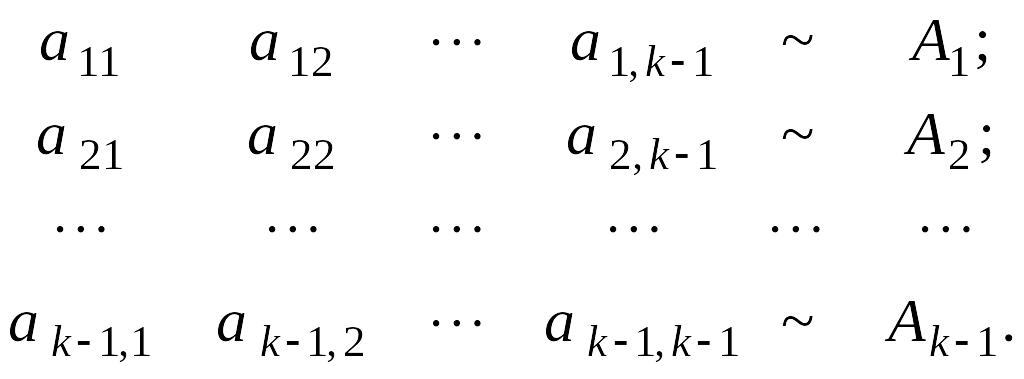
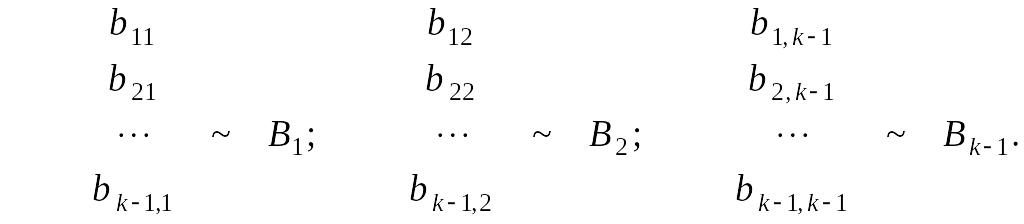
Тогда

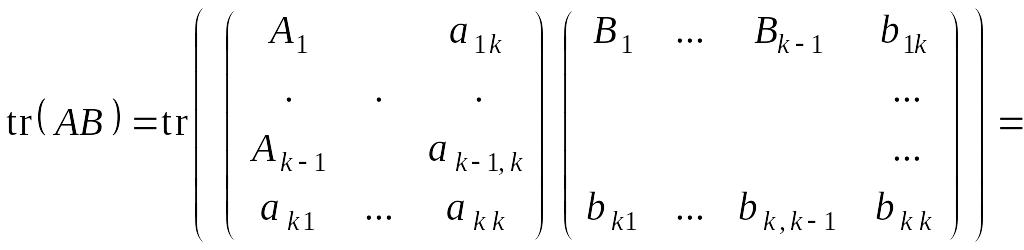
Аналогично

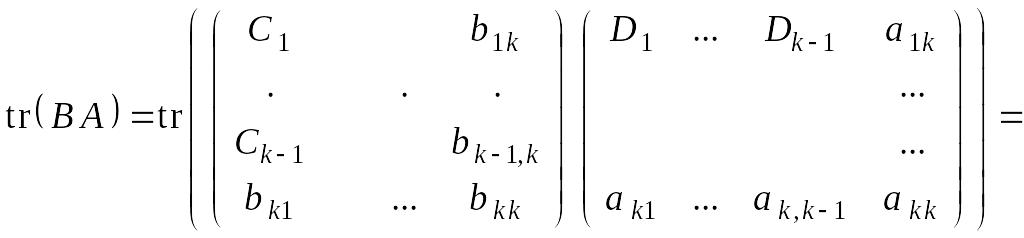
Заметим,
что

– матрицы
порядка n – 1 и

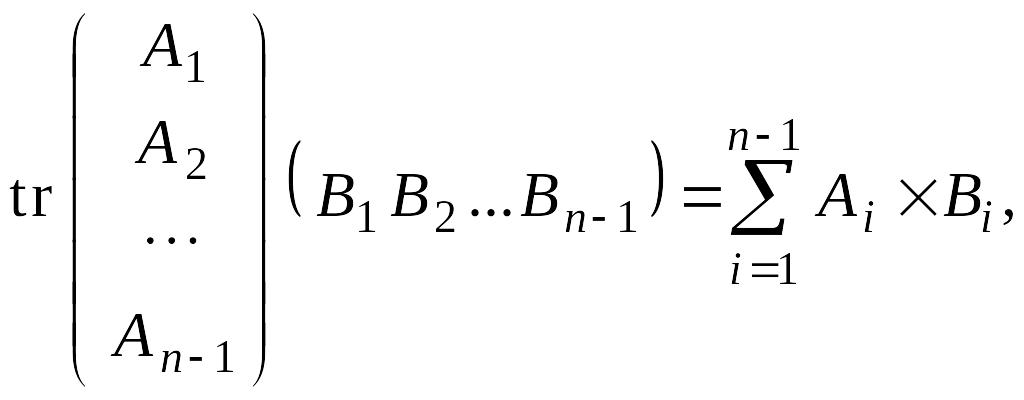
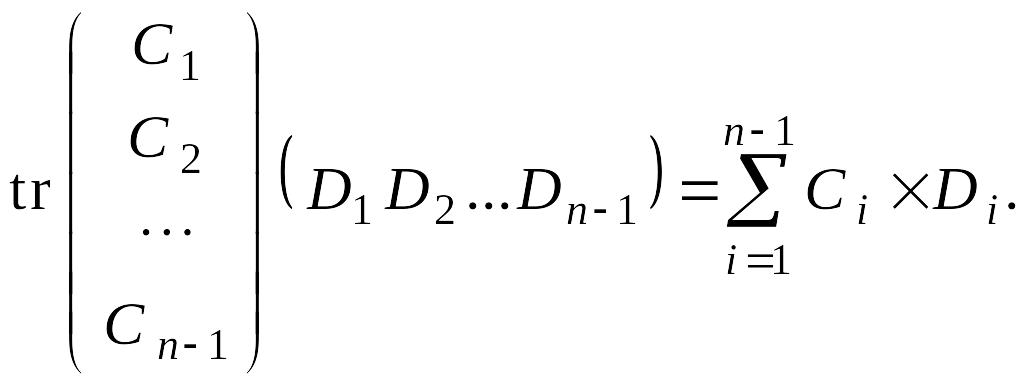
В силу индуктивного
предположения 2

Отсюда следует равенство

.

Упражнение
3. Пусть А – матрица размерности

,
причем

.
Вычислить

,
где

.

Решение.
Пусть

–
жорданова форма матрицы А и

–
ее собственные значения, тогда

Так
как

– верхняя треугольная матрица и на ее
главной диагонали стоят элементы

то

Значит,

согласно задаче 14 (см. задачи для
самостоятельного решения ниже) ,

Итак,

Последнее
равенство доказано в примере 1 пункта
3.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com

Источник

Иногда может возникнуть необходимость выполнить возведение матрицы в степень. В этой статье мы рассмотрим, каким образом и в каком порядке выполняется данная операция.

Если говорить простыми словами, то вся суть возведения матрицы в степень n заключается в том, чтобы умножить матрицу на саму себя, сделав это n-е число раз. Однако существует ряд условий:

— правило справедливо лишь для квадратных матриц, которые имеют одинаковое (равное) число строк и столбцов;

— показатель степени должен быть натуральным (2, 3, 4, 5, 6, 7…).

Квадрат матрицы

Для примера давайте возведем матрицу в квадрат (то есть во вторую степень). Представим, что у нас есть квадратная матрица А². Как уже было сказано выше, для получения нужного результата ее нужно умножить на саму себя:

Исходные данные:

В каком порядке и как нужно выполнять расчет, чтобы возвести А в квадрат?

Представьте, что строки 1-й матрицы представляют собой столики в кафетерии. Тогда столбцы 2-й матрицы (ниже обозначены разными цветами) — это официанты. Поначалу «столики обслуживают» официанты из красного столбца, потом зеленого, потом синего. Таким образом происходит последовательный перебор столбцов слева направо. Вот такой вот мысленный прием.

Решение:

Напоследок скажем, что сегодня существует множество онлайн-калькуляторов, позволяющих выполнять широкий спектр математических матричных операций:

— возведение матриц в степень;

— умножение на число;

— сложение и вычитание;

— транспонирование;

— нахождение обратной матрицы;

— нахождение ранга и определителя.

На этом все, очень надеемся, что у вас больше не будет возникать вопросов о том, как и в каком порядке возводить матрицу в степень.

По материалам:

https://studwork.org/spravochnik/matematika/matricy/vozvedenie-matricy-v-stepen;
http://www.mathprofi.ru/svoistva_operacij_nad_matricami_matrichnye_vyrazheniya.html.

Источник

Возведение матриц в степень и многочлены от матриц

Возведение матриц в степень

Для любой квадратной матрицы (n-ro порядка) определено произведение Acdot A (матрицы на себя). Поэтому можно говорить о целой неотрицательной степени матрицы, определяя последовательно

$A^0=E,quad A^1=A,quad A^2=Acdot A,quad A^3=A^2cdot A,~ldots,~A^m=A^{m-1}cdot A,~ldots$

Заметим, что степени A^k и $A^{ell}$ одной и той же матрицы перестановочны

$begin{aligned}A^kcdot A^{ell}&= underbrace{begin{pmatrix}Acdot Acdotldotscdot Aend{pmatrix}}_{k}cdot underbrace{begin{pmatrix}Acdot Acdotldotscdot Aend{pmatrix}}_{ell}= underbrace{Acdot Acdotldotscdot A}_{k+ell}= A^{k+ell};\[5pt] A^{ell}cdot A^{k}&= underbrace{begin{pmatrix}Acdot Acdotldotscdot Aend{pmatrix}}_{ell}cdot underbrace{begin{pmatrix}Acdot Acdotldotscdot Aend{pmatrix}}_{k}= underbrace{Acdot Acdotldotscdot A}_{ell+k}= A^{k+ell}.end{aligned}$

Поэтому справедливы обычные свойства степеней:

$A^kcdot A^{ell}=A^{ell}cdot A^k=A^{k+ell},~~(A^k)^{ell}=A^{kell},$ с натуральными показателями.

Многочлены от матриц

При помощи операций возведения в степень, сложения матриц и умножения матрицы на число можно получать многочлены от матриц. Пусть p_m(x)=a_0+a_1x+a_2x^2+ldots+a_mx^m — многочлен (степени ) переменной , — квадратная матрица n-го порядка. Выражение вида

$p_m(A)=a_0underbrace{E}_{A^0}+a_1A+a_2A^2+ldots+a_mA^m$

называется многочленом от матрицы . Многочлен P_m(A) является квадратной матрицей n-го порядка.

Пример 1.14. Найти A^3 , если $A= begin{pmatrix}1&2\1&1end{pmatrix}$ .

Решение. По определению степени матрицы получаем

$A^3= {begin{pmatrix}1&2\1&1end{pmatrix}!}^3= begin{pmatrix}1&2\1&1end{pmatrix}!cdot! begin{pmatrix}1&2\1&1end{pmatrix}!cdot! begin{pmatrix}1&2\1&1end{pmatrix}= begin{pmatrix}3&4\2&3end{pmatrix}!cdot! begin{pmatrix}1&2\1&1end{pmatrix}= begin{pmatrix}7&10\5&7end{pmatrix}!.$

Пример 1.15. Найти f(A) , если $f(x)=x^2-5x+3,~ A= begin{pmatrix}2&-1\-3&3end{pmatrix}$ .

Решение. Используем определение многочлена от матрицы:

$begin{aligned}f(A)&= begin{pmatrix}2&-1\-3&3end{pmatrix}!cdot! begin{pmatrix}2&-1\-3&3end{pmatrix}-5cdot! begin{pmatrix}2&-1\-3&3end{pmatrix}+3cdot! begin{pmatrix}1&0\0&1end{pmatrix}=\[3pt] &= begin{pmatrix}7&-5\-15&12end{pmatrix}- begin{pmatrix}10&-5\-15&15end{pmatrix}+ begin{pmatrix}3&0\0&3end{pmatrix}= begin{pmatrix}0&0\0&0end{pmatrix}!.end{aligned}$

Пример 1.16. Найти A^n , если $A= begin{pmatrix}lambda&1\0&lambdaend{pmatrix}!,~ninmathbb{N}$ .

Решение. По определению степени матрицы последовательно находим:

$begin{gathered}A^2= begin{pmatrix}lambda&1\0&lambdaend{pmatrix}!cdot! begin{pmatrix}lambda&1\0&lambdaend{pmatrix}= begin{pmatrix}lambda^2&2lambda\0&lambda^2end{pmatrix}!;\[3pt] A^3=A^2cdot A= begin{pmatrix}lambda^2&2lambda\0&lambda^2end{pmatrix}!cdot! begin{pmatrix}lambda&1\0&lambdaend{pmatrix}= begin{pmatrix}lambda^3&3lambda^2lambda\0&lambda^3end{pmatrix}!.end{gathered}$

Предполагаем, что $A^n= begin{pmatrix}lambda^n&nlambda^{n-1}\0&lambda^nend{pmatrix}$ . Докажем эту формулу по индукции

Действительно, при n=1 формула верна. Теперь, предполагая, что для любого натурального формула верна, докажем ее справедливость для (n+1) . В самом деле,

$A^{n+1}=A^ncdot A= begin{pmatrix}lambda^n&nlambda^{n-1}\0&lambda^nend{pmatrix}!cdot! begin{pmatrix}lambda&1\0&lambdaend{pmatrix}= begin{pmatrix}lambda^{n+1}&(n+1)lambda^{n}\0&lambda^{n+1}end{pmatrix}!.$

Следовательно, $A^n= begin{pmatrix} lambda^n& nlambda^{n-1}\ 0&lambda^nend{pmatrix}$ для любого натурального .

Из перестановочности степеней одной и той же матрицы следует, что многочлены от одной и той же матрицы перестановочны. Действительно, если

p(x)=a_0+a_1x+a_2x^2+ldots+a_mx^m и q(x)=b_0+b_1x+b_2x^2+ldots+b_nx^n , то

$begin{gathered}p(A)cdot q(A)= left(sum_{i=0}^{m}a_iA^iright)!!left(sum_{j=0}^{n}b_jA^jright)= sum_{i=0}^{m}sum_{j=0}^{n}a_ib_jA^iA^j=\[3pt] =sum_{j=0}^{n}sum_{i=0}^{m}b_ja_iA^jA^i= left(sum_{j=0}^{n}b_jA^jright)!! left(sum_{i=0}^{m}a_iA^iright)= q(A)cdot p(A),end{gathered}$

что и требовалось показать.

Со степенью матрицы связаны следующие определения, характеризующие ее свойства. Квадратная матрица А называется

– идемпотентной, если A^2=A ;

– инволютивной, если A^2=E ;

– периодической, если A^k=E при некотором натуральном (число называется периодом матрицы );

– нильпотентной, если A^k=O при некотором натуральном (число называется показателем нильпотентности матрицы ).

Пример 1.17. Даны матрицы:

$A= begin{pmatrix}-26&-18&-27\21&15&21\12&8&13end{pmatrix}!,quad B= begin{pmatrix}-53&-36&-54\42&29&42\24&16&25end{pmatrix}!,quad J= begin{pmatrix}0&1&0\0&0&1\0&0&0end{pmatrix}!.$

Показать, что матрица — идемпотентная, — инволютивная (периодическая), — нильпотентная. Найти многочлены P(A),P(B),P(J) от этих матриц, если P(x)=x^2+2x+3 .

Решение. Находим степени матриц

$begin{aligned}A^2&= begin{pmatrix}-26&-18&-27\21&15&21\12&8&13end{pmatrix}!cdot! begin{pmatrix}-26&-18&-27\21&15&21\12&8&13end{pmatrix}= begin{pmatrix}-26&-18&-27\21&15&21\12&8&13end{pmatrix}=A;\[3pt] B^2&= begin{pmatrix}-53&-36&-54\42&29&42\24&16&25end{pmatrix}!cdot! begin{pmatrix}-53&-36&-54\42&29&42\24&16&25end{pmatrix}= begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=E;\[3pt] J^2&= begin{pmatrix}0&1&0\0&0&1\0&0&0end{pmatrix}!cdot! begin{pmatrix}0&1&0\0&0&1\0&0&0end{pmatrix}= begin{pmatrix}0&0&1\0&0&0\0&0&0end{pmatrix}!;\[3pt] J^3&=J^2cdot J= begin{pmatrix}0&0&1\0&0&0\0&0&0end{pmatrix}!cdot! begin{pmatrix}0&1&0\0&0&1\0&0&0end{pmatrix}= begin{pmatrix}0&0&0\0&0&0\0&0&0end{pmatrix}=O.end{aligned}$

Следовательно, матрица — идемпотентная, — инволютивная (периодическая с периодом 2), — нильпотентная (с показателем 3).

По определению находим многочлены

$begin{gathered}P(A)= A^2+2A+3E= A+2A+3E=3(A+E)= begin{pmatrix}-75&-54&-81\63&48&63\ 36&24&42end{pmatrix}!;\[3pt] P(B)=B^2+2B+3E=E+2B+3E=2B+4E= begin{pmatrix}-102&-72&-108\84&62&84\48&32&54end{pmatrix}!;\[3pt] P(J)=J^2+2J+3E= begin{pmatrix}0&0&1\0&0&0\0&0&0end{pmatrix}+ begin{pmatrix}0&2&0\0&0&2\0&0&0end{pmatrix}+ begin{pmatrix}3&0&0\0&3&0\0&0&3end{pmatrix}= begin{pmatrix}3&2&1\0&3&2\0&0&3end{pmatrix}!.end{gathered}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник