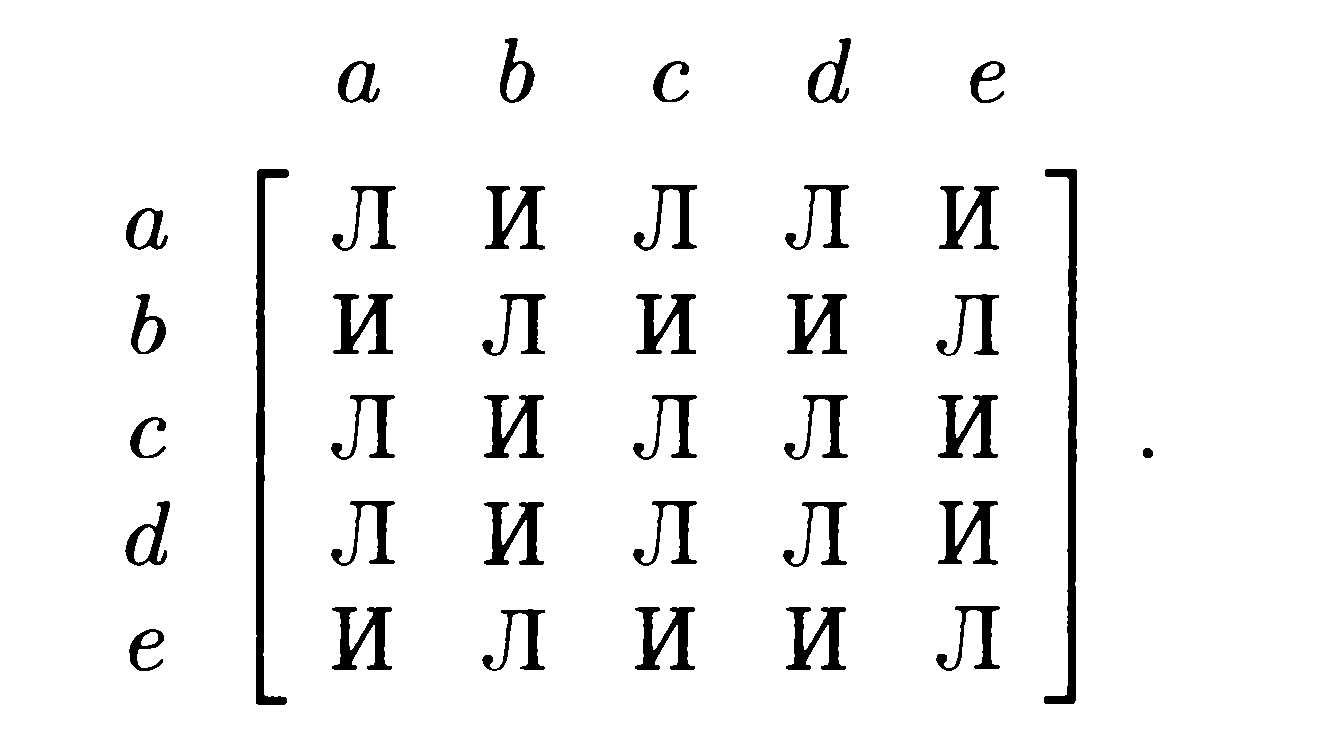Как найти степени вершин для графов - Исправление недочетов и поиск решений вместе с Examum.ru

Определение
7.10. Степенью
вершины v
для неориентированного графа, обозначается
d(v),
называется количество ребер, инцидентных
этой вершине. Вершина степени 0 называется
изолированной.
Вершина степени 1 называется висячей.

Определение
7.11. Полустепенью
исхода вершины
v
для орграфа
называется количество дуг, для которых
v
является начальной вершиной, обозначается
.

Полустепенью
захода
вершины v
называется количество дуг, для которых
v
является конечной вершиной, обозначается
.
Если,
то вершинаv
называется истоком.
Если
,
то вершинаv
называется стоком.

Теорема 7.2.
(Теорема
Эйлера)
Сумма степеней вершин графа равна
удвоенному количеству ребер:

Доказательство.
При подсчете суммы степеней вершин
каждое ребро учитывается два раза: для
одного конца ребра и для другого.

Следствие 1.
Число вершин нечетной степени четно.

Доказательство.
По теореме Эйлера сумма степеней всех
вершин – четное число. Сумма степеней
вершин четной степени четна, значит,
сумма степеней вершин нечетной степени
также четна, следовательно, их четное
число.

Следствие 2.
Сумма полустепеней вершин орграфа
равна удвоенному количеству дуг:

Доказательство.
Сумма полустепеней вершин орграфа
равна сумме степеней вершин графа,
полученного из орграфа забыванием
ориентации дуг.

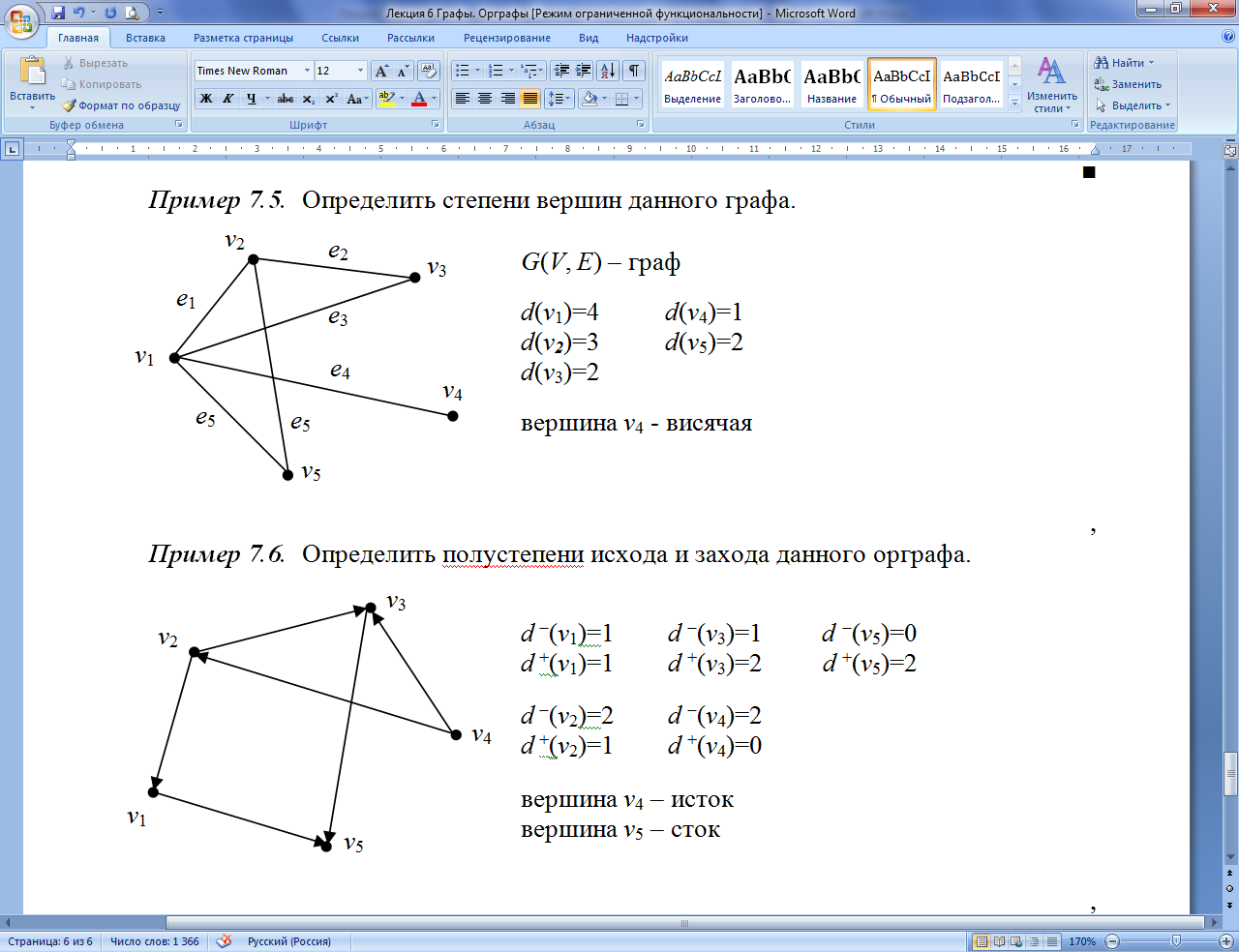
Пример 7.5.
Определить степени вершин данного
графа.

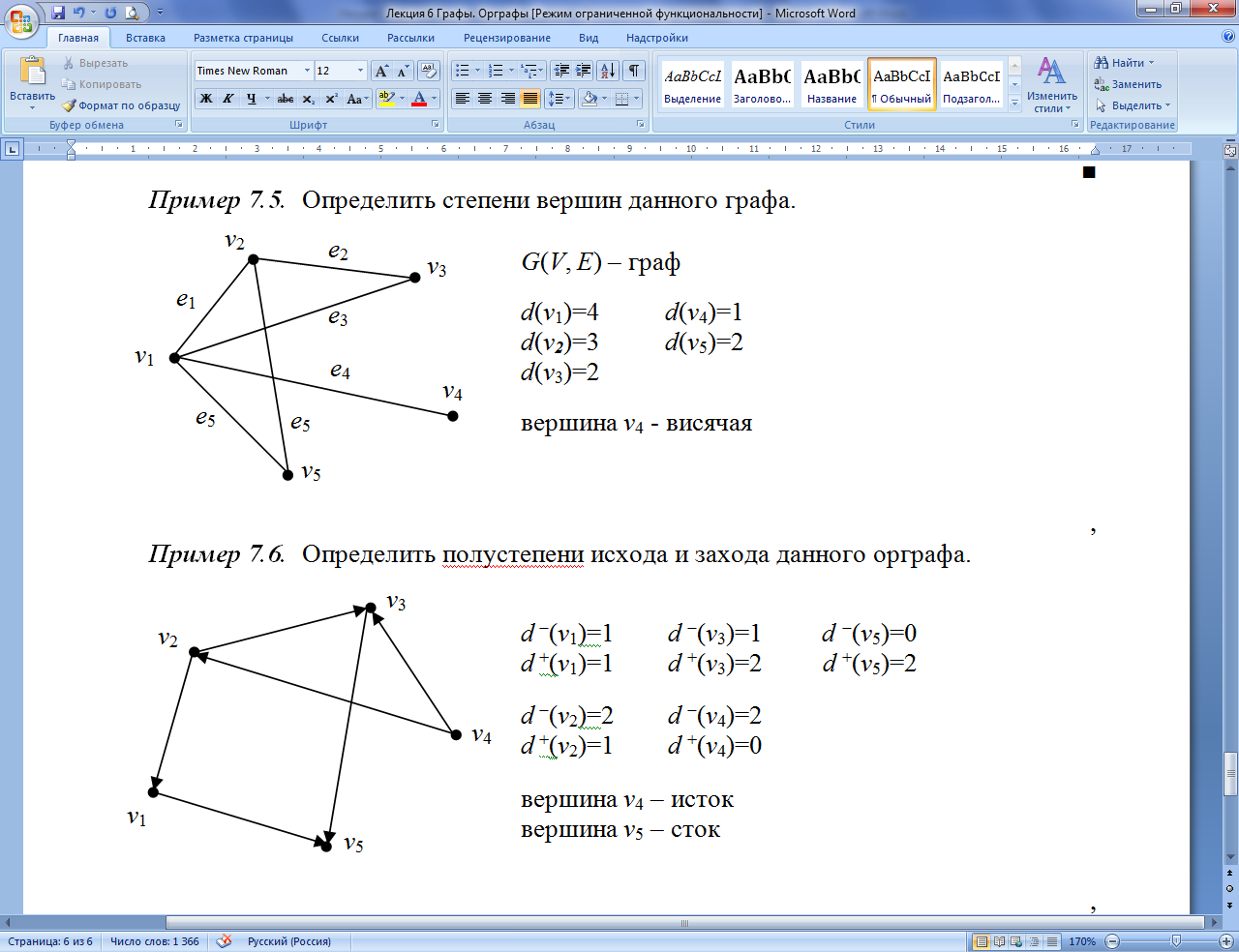
Пример 7.6.
Определить полустепени исхода и захода
данного орграфа.

7.5. Представление (способы задания) графов.

Граф
как алгебраическая система:

модель, носителем
которой является множество вершин, а
отношение – бинарное отношение смежности
вершин.

< {a,b,c,d};
— множество
вершин

{(a,b),(b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}
– множество
рёбер
>

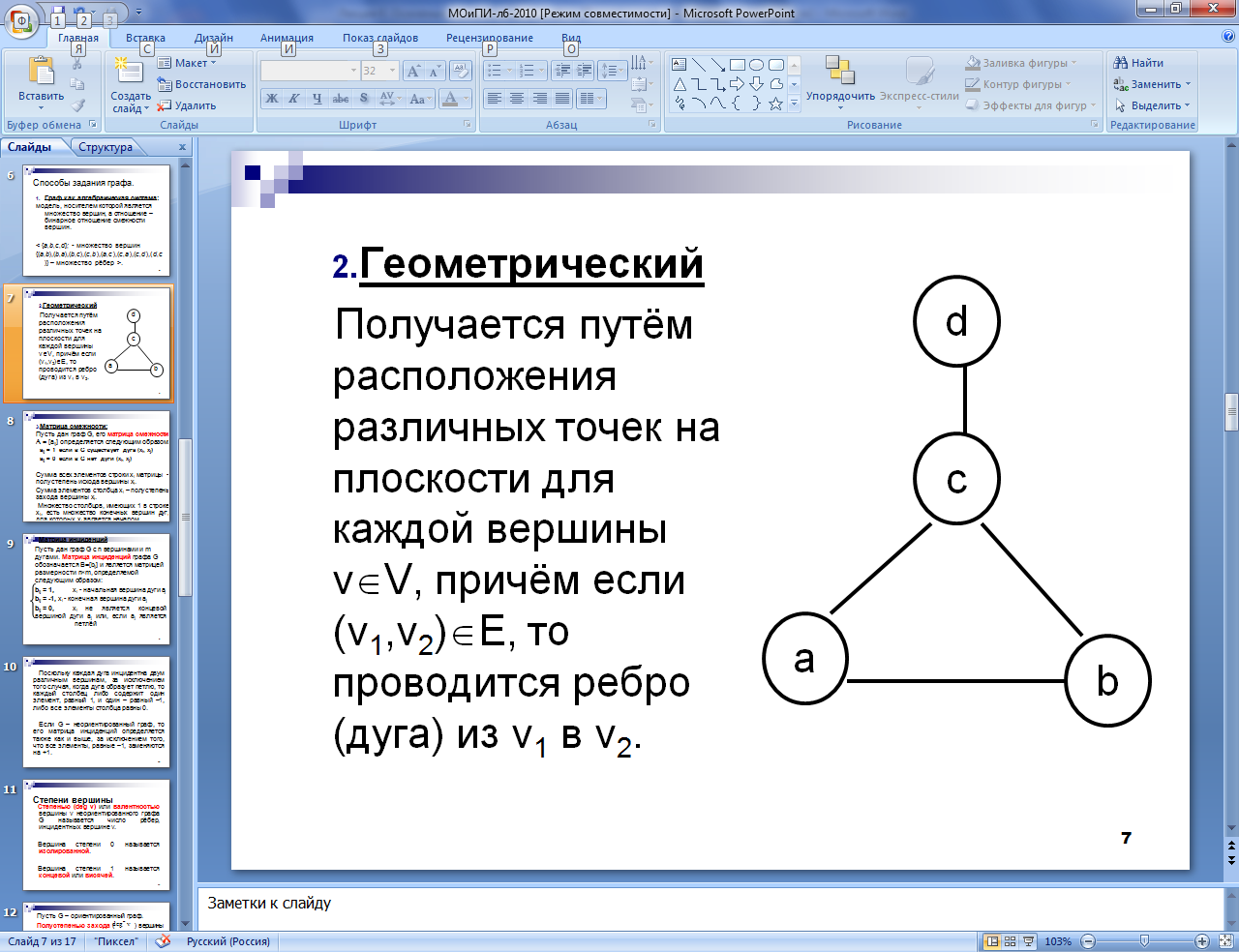
Геометрический

Получается путём
расположения различных точек на
плоскости для каждой вершины vÎV,
причём если (v₁,v₂)ÎЕ,
то проводится ребро (дуга) из v₁
в v₂.

Для представления
в компьютере чаще всего граф задается
либо матрицей
смежности,
либо матрицей
инциденций.

Матрицей
смежности вершин неориентированного
графа
G,
содержащего n
вершин, называют квадратную матрицу
A=a_ij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам
неориентированного графа.

Элементы a_ij
матрицы A
равны числу ребер, направленных из i-й
вершины в j-ю.
В случае неориентированного
графа G
ему вместе с ребром (v_i,
v_j)
принадлежит и ребро (v_j,
v_i),
поэтому матрица смежности вершин
A=a_ij
будет симметрична относительно главной
диагонали.

ПРИМЕР.
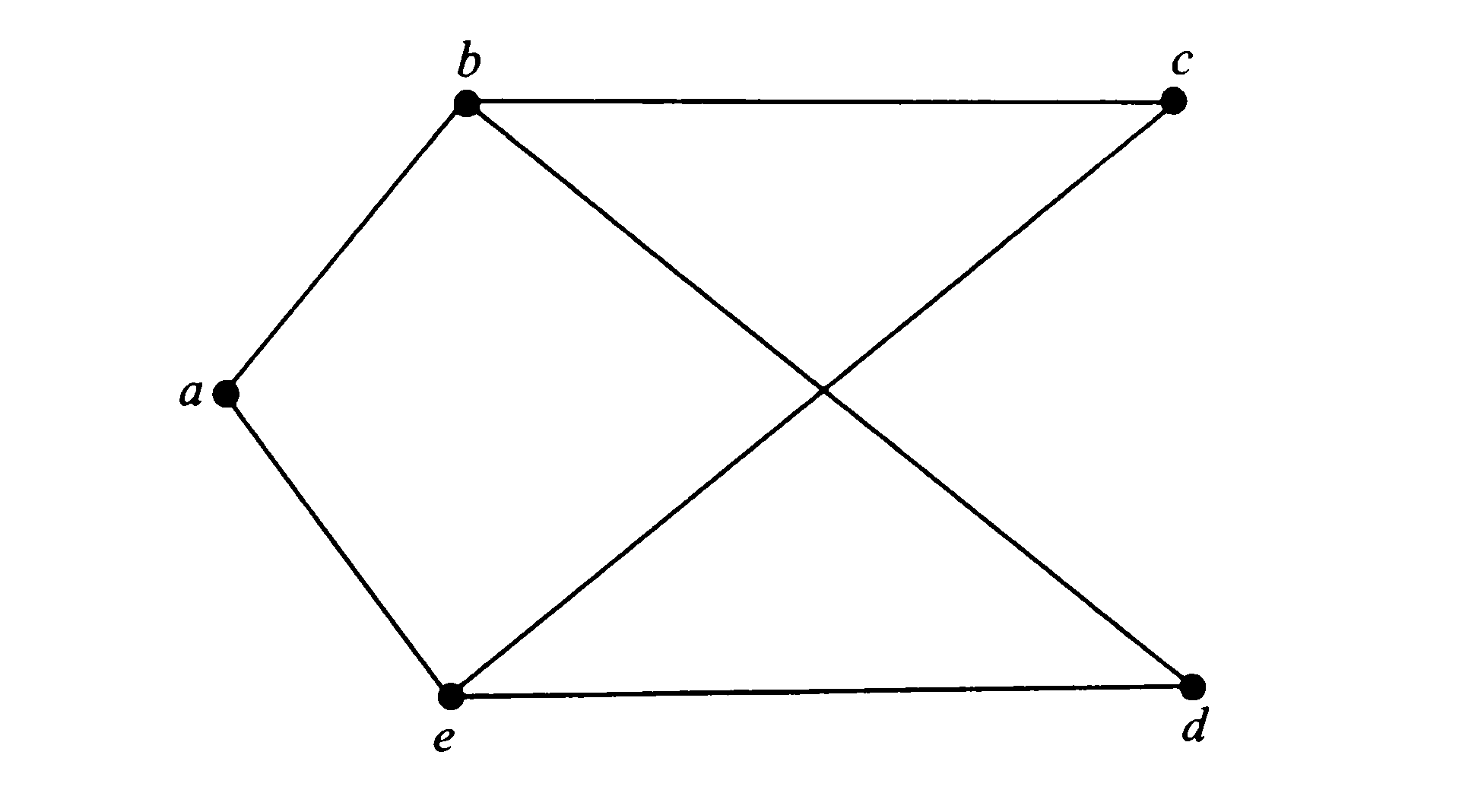
Граф: множество вершин V
= {a,b,c,d,e}

Множество
ребер

Е
= {{а, b},
{а, е}, {b,
c},
{b,
d},
{c,
e},
{d,e}},

Матрица смежности
симметрична относительно главной
диагонали.

На главной диагонали
стоит 1 (символ Л) из-за
нерефлексивности
отношения на множестве вершин (EÍV´V)

Логическая матрица
отношения на множестве вершин графа,
которое задается его ребрами.

a b c d

a 0 1 0 1

b 1 0 1 1

с 0 1 0 1

d 1 1 1 0

простой
граф

a b c d

a 1 1 0 1

b 1 0 3 0

c 0 3 0 2

d 1 0 2 0

граф
с кратными

рёбрами
и петлёй

Определение
7.12. Матрица
смежности вершин орграфа
G,
содержащего n
вершин-
это квадратная матрица A=a_ij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам орграфа.

Элементы a_ij
матрицы A
равны числу дуг, направленных из i-й
вершины в j-ю.
Если орграф состоит из однократных
дуг, то элементы матрицы равны либо 0,
либо 1.

Матрица
смежности:

Пусть дан граф G,
его матрица
смежности
А = [a_ij]
определяется следующим образом:

a_ij
= 1 если в G
существует дуга (x_i,
x_j)

a_ij
= 0 если в G
нет дуги (x_i,
x_j)

Определение
7.14. Матрицей
инциденций (инцидентности) неориентированного
графа с
вершинами
и
ребрами
называется
матрица
размерности,
строки которой соответствуют вершинам,
а столбцы – ребрам. Элементыматрицы инциденций неориентированного
графа равны 1, если вершинаинцидентна ребру,
и 0 в противном случае.

Матрицей
инциденций (инцидентности) орграфа с
вершинами
и
дугами
называется
матрица
размерностиnm,
строки которой соответствуют вершинам,
а столбцы -дугам
орграфа.

Элементы c_ij
равны

1, если дуга e_j
исходит из i-й
вершины;

–1, если дуга e_j
заходит в i-ю
вершину;

0, если дуга не
инцидентна i-й
вершине

Поскольку каждая
дуга инцидентна двум различным вершинам,
за исключением того случая, когда дуга
образует петлю, то каждый столбец либо
содержит один элемент, равный 1, и один
– равный –1, либо все элементы столбца
равны 0.

Степень вершины
равна сумме элементов строки, обозначенной
этой вершиной, так как каждая единица
в этой строке представляет инцидентность
этой вершины ребру.

В каждом столбце
также будут две единицы, так как каждое
ребро инцидентно двум вершинам.

Матрицы инцидентности
не имеют большого значения при
рассмотрении ориентированных графов,
т.к. они не содержат информации о том,
как ребро ориентировано.

Поэтому, используя
матрицу инцидентности, нельзя восстановить
ориентированный граф.

Такую возможность
обеспечивает матрица смежности,

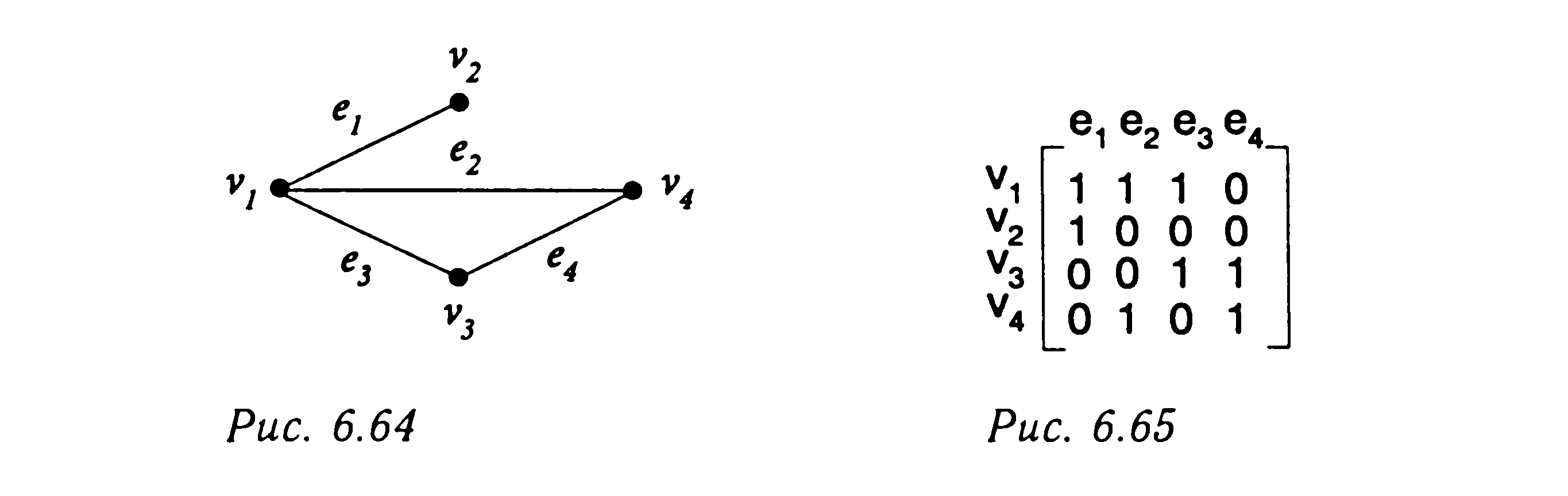
Пример
7.7.1.
Для заданного неориентированного
графа построить матрицы смежностей и
матрицу инциденций.

Решение.
1) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

2) Строим матрицу
инциденций, которая будет размерности
45.

Пример
7.7.2.
Для заданного ориентированного графа
построить матрицы смежностей и матрицу
инциденций.

2) Строим матрицу
инциденций, которая будет размерности
45.

Источник

Степень вершины (теория графов)

Степень вершины (англ. degree , также валентность, англ. valency ) в теории графов — количество рёбер графа , инцидентных вершине . При подсчёте степени ребро-петля учитывается дважды. [1] Степень вершины обозначается как d(x) (в западных источниках — deg(v) ). Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G). На рис. 1 максимальная степень равна 5, минимальная — 0. В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.

Содержание

Лемма о рукопожатиях

По формуле суммы степеней для графа ,

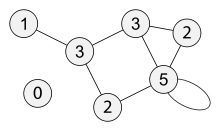
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью. [2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.

Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence ). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.

Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность d_i (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство

Здесь точка – это точка с именем «а».

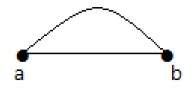
Линия

Линия – это связь между двумя точками. Это может быть представлено сплошной линией.

пример

Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.

Вершина – это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.

пример

Здесь вершина названа с алфавитом «а».

Ребро – это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.

пример

Здесь «a» и «b» – две вершины, и связь между ними называется ребром.

график

Граф ‘G’ определяется как G = (V, E), где V – множество всех вершин, а E – множество всех ребер графа.

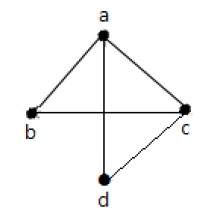
Пример 1

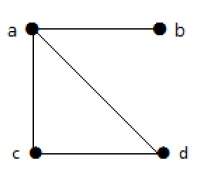
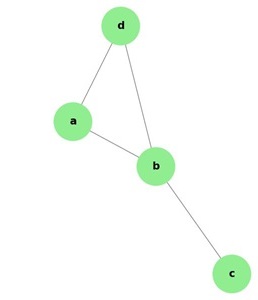
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.

Пример 2

graph1

В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.

петля

В графе, если ребро нарисовано от вершины к себе, это называется циклом.

Пример 1

На приведенном выше графике V – вершина, для которой у нее есть ребро (V, V), образующее петлю.

Пример 2

В этом графе есть две петли, которые сформированы в вершине a, и вершине b.

Степень вершины

Это число вершин, смежных с вершиной V.

Обозначение – град (V).

В простом графе с n числом вершин степень любых вершин равна –

Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.

Степень вершины можно рассматривать по двум случаям графов –

Ненаправленный граф
Направленный граф

Степень вершины в неориентированном графе

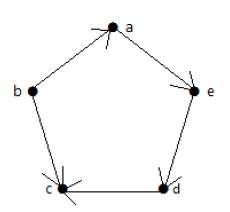
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.

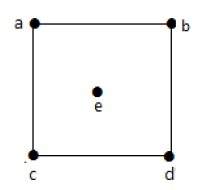
Пример 1

Посмотрите на следующий график –

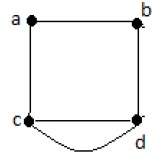
На приведенном выше неориентированном графике

deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

Итак, «c» – это вершина с кулоном .

deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

Так что «е» – изолированная вершина .

deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

Итак, «c» – это вершина с кулоном .

deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

Так что «е» – изолированная вершина .

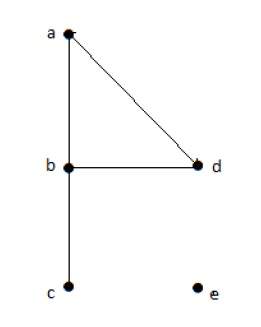
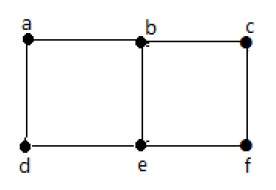
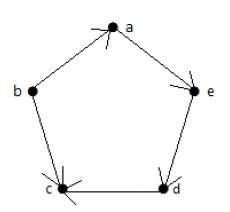
Пример 2

Посмотрите на следующий график –

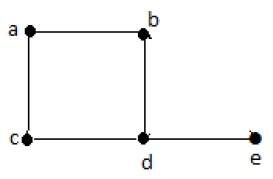
На приведенном выше графике

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.

Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.

Степень вершины в ориентированном графе

В ориентированном графе каждая вершина имеет степень и степень.

Степень графа

Степень вершины V – это количество ребер, входящих в вершину V.

Обозначение – град – (V).

Степень вершины V – это количество ребер, входящих в вершину V.

Обозначение – град – (V).

Степень графа

Отступ вершины V – это число ребер, выходящих из вершины V.

Обозначение – град + (V).

Отступ вершины V – это число ребер, выходящих из вершины V.

Обозначение – град + (V).

Рассмотрим следующие примеры.

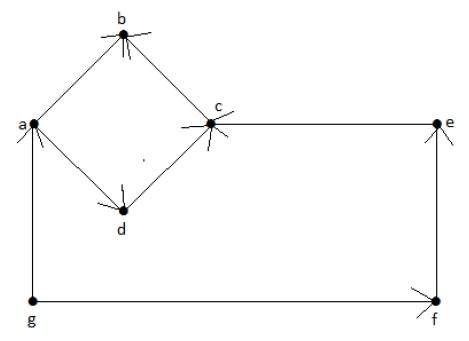
Пример 1

Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
1	2
б	2	0
с	2	1
d	1	1
е	1	1
е	1	1
г	0	2

Пример 2

Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
1	1
б	0	2
с	2	0
d	1	1
е	1	1

Кулон Вертекс

Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.

пример

Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.

Изолированная вершина

Вершина с нулевой степенью называется изолированной вершиной.

пример

Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.

смежность

Вот нормы смежности –

В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.

В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

Пример 1

На приведенном выше графике –

«a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».

«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

«a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».

«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

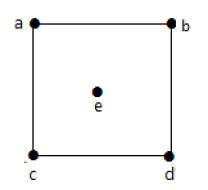
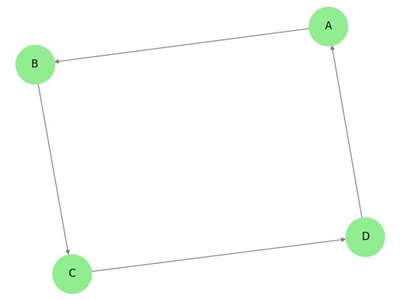
Пример 2

На приведенном выше графике –

a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

Параллельные края

В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.

На приведенном выше графике «a» и «b» – это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.

Мульти График

Граф, имеющий параллельные ребра, называется мультиграфом.

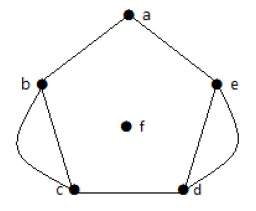
Пример 1

На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.

Пример 2

На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.

Степень последовательности графика

Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.

Пример 1

темя	б	с	d	е
Присоединенный к	До нашей эры	объявление	объявление	с, Ь, е	d
степень	2	2	2	3	1

На приведенном выше графике для вершин последовательность степеней равна .

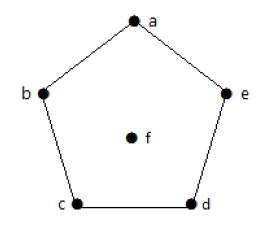
Пример 2

темя	б	с	d	е	е
Присоединенный к	быть	а, с	б, г	с, е	объявление	–
степень	2	2	2	2	2	0

На приведенном выше графике для вершин последовательность степеней равна .

«Степень вершины и подсчет числа ребер графа». 7-й класс

Назад Вперёд

Загрузить презентацию (487 кБ)

Профиль класса: общеобразовательный.

Тип урока: изучение и первичное закрепление новых знаний.

ученик знает понятия графа и мультиграфа, знаком с понятиями “вершина графа” (смежные вершины) и “ребро графа” (кратные ребра и петли);
умеет приводить примеры использования графов в различных учебных предметах и повседневной жизни.

закрепить понятие графа, сформировать представление о степени вершины графа (четная, нечетная вершины), сформулировать определение о связности графа, рассмотреть утверждение о количестве ребер графа и теорему о четности числа нечетных вершин графа;
отработать навыки использования теоретических знаний для решения новых задач.

развивать логическое мышление учащихся, способность к рассуждению, внимательность;
формировать умение представлять информацию в виде графов.

воспитывать культуру общения на уроке, взаимоуважение.

Организационный момент (приветствие класса, подготовка к уроку, проверка домашнего задания, включающая повторение материала предыдущего урока);
Теоретический материал (знакомство с темой предстоящего урока, объяснение нового материала и краткая запись в рабочую тетрадь новых теоретических сведений по теме урока);
Закрепление материала (решение задач);
Итоги урока (краткий вывод и домашнее задание).

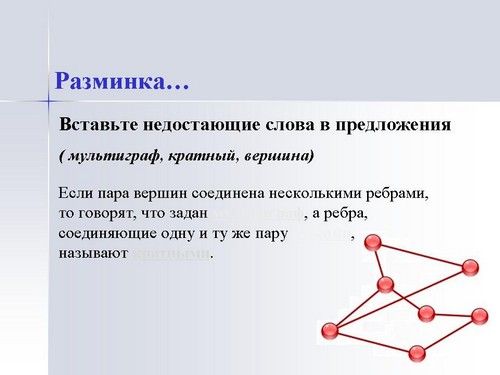
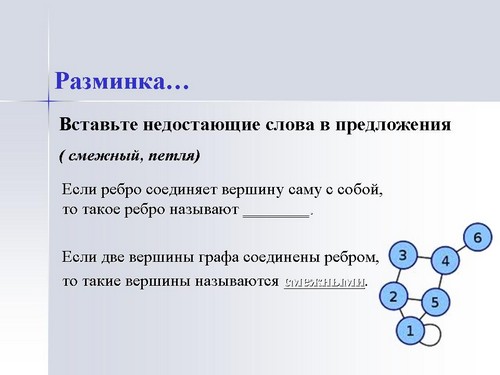
Давайте вспомним основные понятия теории графов. Для этого проведем разминку по типу незаконченного предложения (Презентация, сл.: 2, 3, 4). Каждый ученик имеет карточки с пропущенными словами в предложение. Учитель зачитывает предложение, останавливаясь перед пропущенным словом, и выбирает ученика, который в свою очередь должен поднять карточку. Далее этот ученик читает дальше предложение, также останавливаясь перед пропущенным словом, и уже сам выбирает одноклассника для ответа и т. д. по цепочке.

Проверим в классе решение домашней задачи (Презентация, сл.: 5, 6, 7). Один ученик выходит к доске и рисует граф. Далее мы вместе проверяем ребра (дороги между городами), считаем количество выходящих ребер из каждой вершины и смотрим связи между городами.

Сегодня на уроке мы продолжим изучение графов, познакомимся с понятием “степень вершины графа” и сформулируем определение связности графа (обратим внимание на наш граф из домашнего задания и определим, является ли он связным или нет и почему). Рассмотрим утверждение о количестве ребер графа, и проверим в соответствие с этим утверждением, правильно ли мы посчитали количество ребер графа в домашней задаче. И рассмотрим теорему о четности числа нечетных вершин графа.

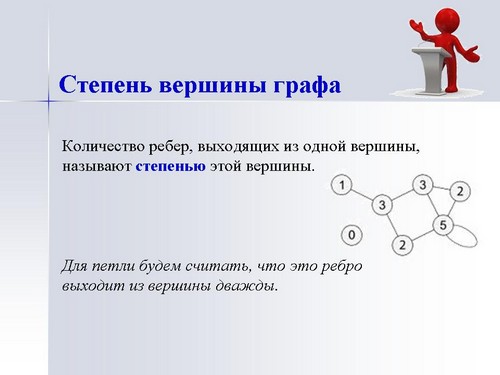
Количество ребер, выходящих из одной вершины, называют степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды (Презентация, сл. 8).

Запишем определение в рабочую тетрадь и зарисуем представленный граф, для данного графа посчитаем степень каждой вершины. Ребята смотрят на слайд и работают самостоятельно, далее вслух зачитаем степень каждой вершины.

Вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной (Презентация, сл. 9).

Запишем определение в тетрадь и перечислим через запятую сначала четные вершины, а потом нечетные вершины для уже нарисованного графа. Проверим задание вслух.

Количество ребер графа равно половине суммы степеней его вершин. Пусть граф имеет n вершин, тогда число ребер равно:

(Презентация, сл. 10)

Запишем утверждение в рабочую тетрадь и посчитаем количество ребер графа в домашней задачке. Проверим ответ в классе. Рассмотрим задачу и ее решение на подсчет числа ребер графа без построения. (Презентация, сл. 11).

Сформулируем теорему о количестве вершин нечетной степени любого графа и запишем формулировку в рабочую тетрадь. (Презентация, сл. 12).

Теорема. Количество вершин нечетной степени любого графа всегда четно.

Доказательство: Количество ребер графа равно половине суммы степеней его вершин.

Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной.

А это возможно только в том случае, если граф содержит четное число нечетных вершин.

Разберем доказательство и проверим теорему на нашей домашней задачке.

Рассмотрим несколько задач.

Задача. В государстве 50 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих дорог из городов: 50 * 4 = 200. Однако, мы понимаем, что при подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 100.

Задача. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?

Ответ. Нет (теорема о четности числа нечетных вершин).

Сегодня мы с вами познакомились с новыми определениями, связанными с понятием графа, рассмотрели утверждение, которое помогает быстро подсчитывать число ребер графа, и сформулировали теорему, которая значительно упрощает решение многих задач. В частности, поучительная сторона этой теоремы заключается в исследовании и ответе на вопрос, возможно или нет решение данной задачи, прежде чем приступать за ее решение.

В качестве домашнего задания ученики получать карточки с тремя задачами (Презентация, сл. 13).

Источник

#include <stdio.h>

#include <stdlib.h>

#include <locale.h>

// количество вершин графа

#define VERTEX_COUNT 9

//———————————————————————

// вычисление степени заданной ( по индексу ) вершины графа

//———————————————————————

int Get_degree_vertex( const int matrix[][ VERTEX_COUNT ], const int index_vertex )

{

int index;

int degree = 0;

for ( index = 0; index < VERTEX_COUNT; index++ )

{

degree += matrix[ index_vertex ][ index ];

}

return degree;

}

//———————————————————————

// вычисление степеней всех вершин заданного графа

//———————————————————————

void Get_degree_vertexes( const int matrix[][ VERTEX_COUNT ], int degrees[] )

{

int index_vertex;

for ( index_vertex = 0; index_vertex < VERTEX_COUNT; index_vertex++ )

{

degrees[ index_vertex ] = Get_degree_vertex( matrix, index_vertex );

}

//———————————————————————

// вывод степеней вершин графа на экран

//———————————————————————

void Print_degrees( const int degrees[] )

{

int index_vertex;

printf( «Степени вершин заданного неориентированного графа:n» );

for ( index_vertex = 0; index_vertex < VERTEX_COUNT; index_vertex++ )

{

printf( «t- вершина #%d имеет степень, равную %dn», index_vertex + 1, degrees[ index_vertex ] );

}

//———————————————————————

// главная функция программы ( точка входа )

//———————————————————————

int main( void )

{

// фиксированная матрица смежности неориентированного графа,

// рассмотренного в статье на сайте

const int matrix[ VERTEX_COUNT ][ VERTEX_COUNT ] =

{

0, 1, 1, 1, 0, 1, 0, 0, 0,

1, 0, 0, 0, 0, 0, 1, 1, 1,

1, 0, 0, 1, 1, 0, 0, 0, 0,

1, 0, 1, 0, 0, 0, 1, 1, 0,

0, 0, 1, 0, 0, 1, 0, 1, 0,

1, 0, 0, 0, 1, 0, 0, 1, 0,

0, 1, 0, 1, 0, 0, 0, 1, 0,

0, 1, 0, 1, 1, 1, 1, 0, 0,

0, 1, 0, 0, 0, 0, 0, 0, 0

};

// массив хранит степени соответсвенных вершин

int degrees[ VERTEX_COUNT ] = { 0 };

// русификация диалогов программы

setlocale( LC_ALL, «Russian» );

// вычисление степеней вершин и вывод результата на экран

Get_degree_vertexes( matrix, degrees );

Print_degrees( degrees );

// задержка работы программы, чтобы у пользователя была возможность просмотреть результат

printf( «nn» );

system( «pause» );

return EXIT_SUCCESS;

}

Источник

It is the number of vertices adjacent to a vertex V.

Notation − deg(V).

In a simple graph with n number of vertices, the degree of any vertices is −

deg(v) = n – 1 ∀ v ∈ G

A vertex can form an edge with all other vertices except by itself. So the degree of a vertex will be up to the number of vertices in the graph minus 1. This 1 is for the self-vertex as it cannot form a loop by itself. If there is a loop at any of the vertices, then it is not a Simple Graph.

Degree of vertex can be considered under two cases of graphs −

Undirected Graph
Directed Graph

Degree of Vertex in an Undirected Graph

An undirected graph has no directed edges. Consider the following examples.

Example 1

Take a look at the following graph −

In the above Undirected Graph,

deg(a) = 2, as there are 2 edges meeting at vertex ‘a’.
deg(b) = 3, as there are 3 edges meeting at vertex ‘b’.
deg(c) = 1, as there is 1 edge formed at vertex ‘c’

So ‘c’ is a pendent vertex.
deg(d) = 2, as there are 2 edges meeting at vertex ‘d’.
deg(e) = 0, as there are 0 edges formed at vertex ‘e’.

So ‘e’ is an isolated vertex.

Example 2

Take a look at the following graph −

In the above graph,

deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, and deg(e) = 0.

The vertex ‘e’ is an isolated vertex. The graph does not have any pendent vertex.

Degree of Vertex in a Directed Graph

In a directed graph, each vertex has an indegree and an outdegree.

Indegree of a Graph

Indegree of vertex V is the number of edges which are coming into the vertex V.
Notation − deg⁻(V).

Outdegree of a Graph

Outdegree of vertex V is the number of edges which are going out from the vertex V.
Notation − deg⁺(V).

Consider the following examples.

Example 1

Take a look at the following directed graph. Vertex ‘a’ has two edges, ‘ad’ and ‘ab’, which are going outwards. Hence its outdegree is 2. Similarly, there is an edge ‘ga’, coming towards vertex ‘a’. Hence the indegree of ‘a’ is 1.

The indegree and outdegree of other vertices are shown in the following table −

Vertex	Indegree	Outdegree
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

Example 2

Take a look at the following directed graph. Vertex ‘a’ has an edge ‘ae’ going outwards from vertex ‘a’. Hence its outdegree is 1. Similarly, the graph has an edge ‘ba’ coming towards vertex ‘a’. Hence the indegree of ‘a’ is 1.

The indegree and outdegree of other vertices are shown in the following table −

Vertex	Indegree	Outdegree
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

Источник

Рис. 1. Граф, на вершинах которого отмечены степени.

Степень вершины (англ. degree, также валентность, англ. valency) в теории графов — количество рёбер графа , инцидентных вершине . При подсчёте степени ребро-петля учитывается дважды.^[1] Степень вершины обозначается как d(x) (в западных источниках — deg(v) ). Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G). На рис. 1 максимальная степень равна 5, минимальная — 0. В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.

Содержание

1 Лемма о рукопожатиях
2 Последовательность степеней вершин
3 Частные значения
4 Общие свойства
5 См. также
6 Примечания
7 Источники

Лемма о рукопожатиях

По формуле суммы степеней для графа ,

$sum_{v in V} deg(v) = 2|E|, ,$

то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, формула утверждает, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других чётно.

Последовательность степеней вершин

Рис. 2. Два неизоморфных графа с одинаковой последовательностью степеней (3, 2, 2, 2, 2, 1, 1, 1).

Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью.^[2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.

Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.

$sum_{i=1}^{k}d_i leq k(k-1) + sum_{i=k+1}^n min(d_i,k) quad k in {1,dots,n} , .$

Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, 2 или 4, но не при k равном 3.

С. Л. Хакими доказал, что (d₁, d₂, …, d_n) есть последовательность степеней простого графа только если существует (d₂ − 1, d₃ − 1, …, d_d₁+1 − 1, d_d₁+2, d_d₁+3, …, d_n). Этот факт позволил разработать простой алгоритм нахождения простого графа с заданной реализуемой последовательностью:

Изначально граф не имеет рёбер.
Составляется список вершин, для которых требования по степеням пока не удовлетворены. Оставшиеся требования располагаются в порядке невозрастания.
Первая вершина соединяется со следующими d₁ вершинами из списка. После этого первая вершина удаляется, список пересортируется. Действие повторяется до тех пор, пока все требования не будут удовлетворены.

Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.

Частные значения

Рис. 3. Концевыми вершинами являются 4, 5, 6, 7, 10, 11 и 12.

Вершина степени 0 называется изолированной.
Вершина степени 1 называется концевой (англ. end vertex), висячей (англ. pendant vertex) или листом графа (англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим (англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных.
Вершина степени n-1 графа порядка n называется доминирующей (англ. dominating vertex).

Общие свойства

Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
Эйлеров путь существует в неориентированном, связном графе если и только если граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
Орграф является псевдолесом только если полустепень захода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени захода всех вершин равны 1.
Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.

См. также

Полустепень захода и полустепень исхода вершин ориентированных графов
Распределение степеней

Примечания

↑ Дистель, стр. 5
↑ Дистель, стр. 278

Источники

Дистель, Рейнхард (2005), «Graph Theory» (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, <http://diestel-graph-theory.com/index.html>.
Эрдёш, П. & Галлаи, T. (1960), ««Gráfok előírt fokszámú pontokkal»», Matematikai Lapok Т. 11: 264—274, <http://www.renyi.hu/~p_erdos/1961-05.pdf>.
Хакими, С. Л. (1962), ««On realizability of a set of integers as degrees of the vertices of a linear graph. I»», Journal of the Society for Industrial and Applied Mathematics Т. 10: 496–506.
Сирксма, Хирард & Хоохефен, Хан (1991), ««Seven criteria for integer sequences being graphic»», Journal of Graph Theory Т. 15 (2): 223–231, DOI 10.1002/jgt.3190150209.

Источник