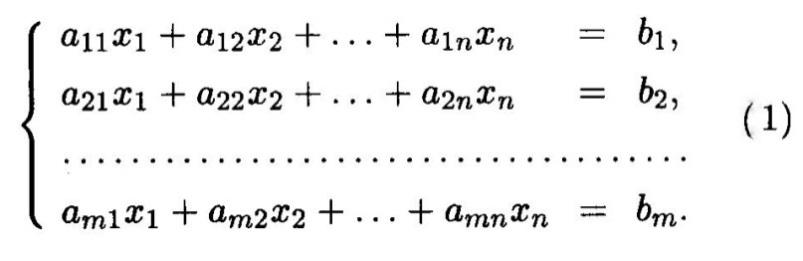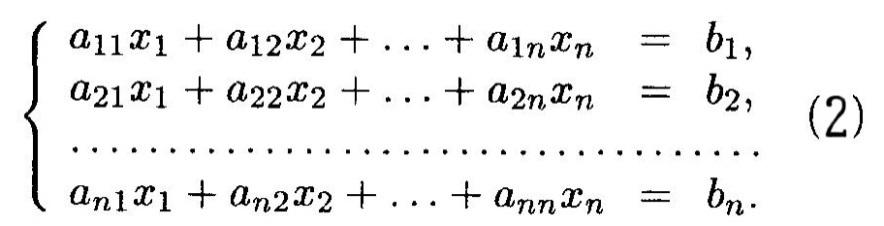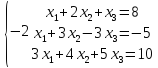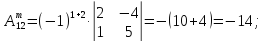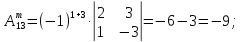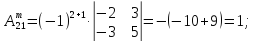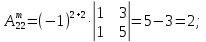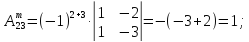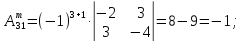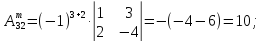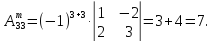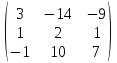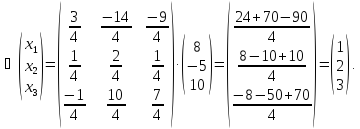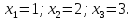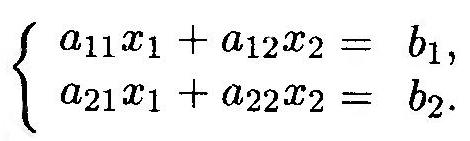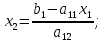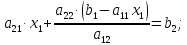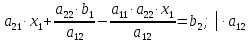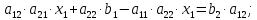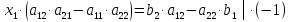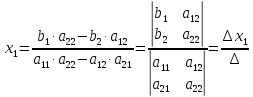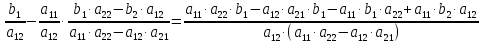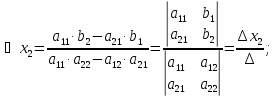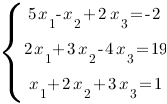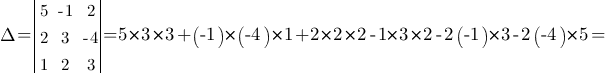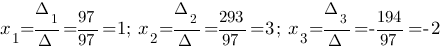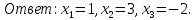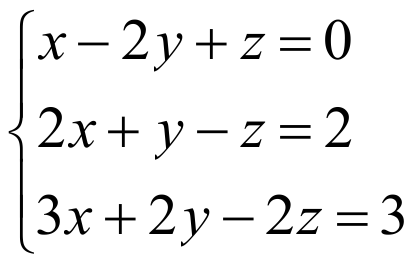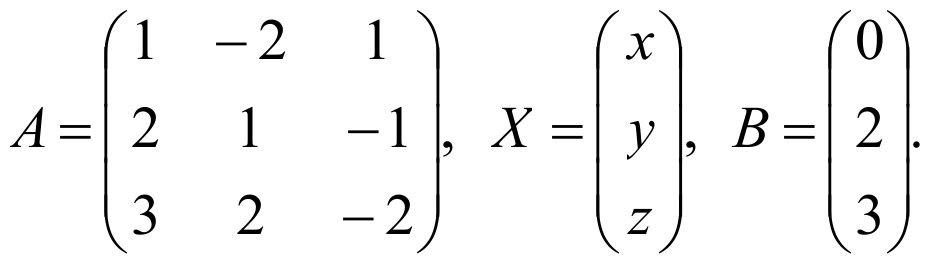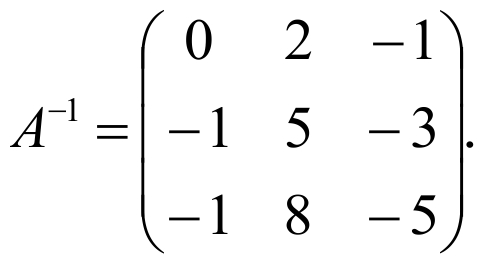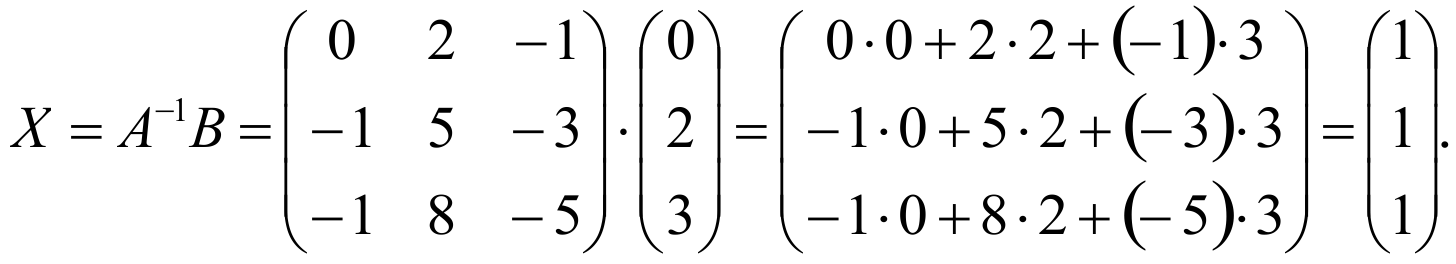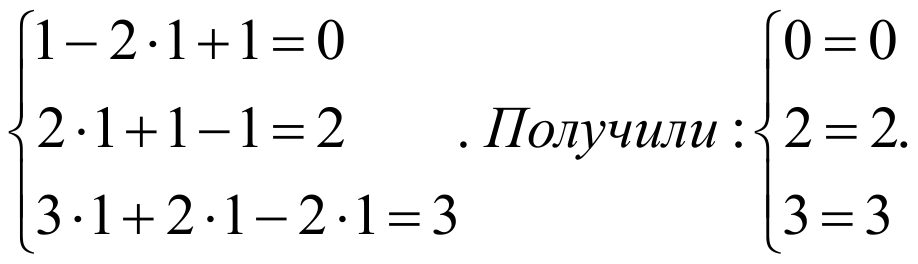Как найти столбец неизвестных в матрице

Вопрос 1. Системы линейных алгебраических уравнений слу (Основные понятия и определения).

1.
Системой m
линейных уравнений с nнеизвестными
называется система
уравнений вида:

2.
Решением
системы уравнений (1) называется
совокупность чисел x₁,
x₂,
… , x_n,
обращающая каждое уравнение системы в
тождество.

3.
Система уравнений (1) называется
совместной,
если она имеет хотя бы одно решение;
если система не имеет решений, она
называется несовместной.

4.
Система уравнений (1) называется
определенной,
если она имеет только одно решение, и
неопределенной,
если у нее более одного решения.

5.
В результате элементарных преобразований
система (1) преобразуется к равносильной
ей системе (т.е. имеющей то же множество
решений).

К
элементарным преобразованиям систем
линейных уравнений относятся:

1.
Отбрасывание нулевых строк.

2.
Изменение порядка строк.

3.
Прибавление к элементам любой строки
элементов другой строки, умноженных на
одно число.

Вопрос 2. Методы решения систем линейных уравнений.

1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.

Системой
n
линейных уравнений с n
неизвестными называется система
уравнений вида:

Запишем
систему (2) в матричном виде, для этого
введем обозначения.

Матрица
коэффициентов перед переменными:

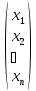
X
=

‒ матрица переменных.

В
=
‒ матрица свободных членов.

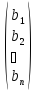
Тогда
система (2)
примет вид:

A×X
= B
‒ матричное уравнение.

Решив
уравнение, получим:

X
= A^-1×B

Пример:

;
;

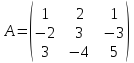
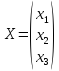
1)
│А│=
15 + 8 ‒18 ‒9 ‒12 + 20 = 4 
0
матрицаА^-1
существует.

2)
A^T=
;

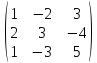
3)

Ã
=

4)
А^-1
=
× Ã =;

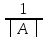
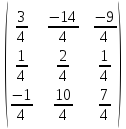
Х
= А^-1
×
B

Ответ:

2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.

Рассмотрим
систему 2 ‒ х линейных уравнений с 2 ‒
мя неизвестными:

Решим
эту систему методом подстановки:

Из
первого уравнения следует:

Подставив
во второе уравнение, получим:

Подставляем
значение
в
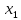
формулу для,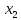
получим:

=

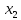
Определитель
Δ — определитель матрицы системы;

Δ
x₁
—
определитель переменной x₁;

Δ
x₂
—
определитель переменной x₂;

Формулы:

x
₁
=;x
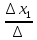
₂
=;…,x_n
=
;Δ

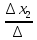
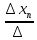
0;

‒
называются
формулами
Крамера.

При
нахождении определителей неизвестных
х₁,
х₂,…,
х_nзаменяется
столбец коэффициентов при той переменной,
определитель которой находят, на столбец
свободных членов.

Пример:
Решить
систему уравнений методом Крамера

Решение: 

Составим
и вычислим сначала главный определитель
этой системы:

Так
как
Δ ≠ 0,
то система имеет единственное решение,
которое можно найти по правилу Крамера:

где
Δ ₁,
Δ ₂,
Δ ₃
получаются
из определителя Δ
путем
замены 1‒ го, 2 ‒ го или 3 ‒ го столбца,
соответственно, на столбец свободных
членов.

Таким
образом:

Лекция № 5

Вопрос 1. Метод Гаусса решения систем линейных уравнений.

Рассмотрим
систему:

Расширенной
матрицей системы (1) называется матрица
вида:

Метод
Гаусса
– это метод последовательного исключения
неизвестных из уравнений системы,
начиная со второго уравнения по m
– тое уравнение.

При
этом путем элементарных преобразований
матрица системы приводится к треугольной
(если m
= n и
определитель системы ≠ 0) или ступенчатой
(если m
< n)
форме.

Затем,
начиная с последнего по номеру уравнения,
находятся все неизвестные.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.   

Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A^-1 · B, где A^-1 — обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A:  A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они  понадобятся для нахождения обратной матрицы.

Теперь найдём союзную матрицу и транспонируем  её, потом подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу  и столбец свободных членов.

Итак, x=2; y=1; z=4.

Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.  

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Матричный способ решения систем линейных уравнений

Рассмотрим систему линейных уравнений следующего вида:

$left{begin{array}{c} {a_{11} x_{1} +a_{12} x_{2} +…+a_{1n} x_{n} =b_{1} } \ {a_{21} x_{1} +a_{22} x_{2} +…+a_{2n} x_{n} =b_{2} } \ {…} \ {a_{n1} x_{1} +a_{n2} x_{2} +…+a_{nn} x_{n} =b_{n} } end{array}right. .$

Числа $a_{ij} (i=1..n,j=1..n)$ — коэффициенты системы, числа $b_{i} (i=1..n)$ — свободные члены.

Каждой СЛАУ можно поставить в соответствие несколько матриц и записать систему в так называемом матричном виде.

Столбец свободных членов образует вектор-столбец, который, как правило, обозначается буквой $B$ и называется матрицей свободных членов.

Неизвестные переменные образуют вектор-столбец, который, как правило, обозначается буквой $X$ и называется матрицей неизвестных.

Описанные выше матрицы имеют вид:

$A=left(begin{array}{cccc} {a_{11} } & {a_{12} } & {…} & {a_{1n} } \ {a_{21} } & {a_{22} } & {…} & {a_{2n} } \ {…} & {…} & {…} & {…} \ {a_{n1} } & {a_{n2} } & {…} & {a_{nn} } end{array}right),B=left(begin{array}{c} {b_{1} } \ {b_{2} } \ {…} \ {b_{n} } end{array}right),X=left(begin{array}{c} {x_{1} } \ {x_{2} } \ {…} \ {x_{n} } end{array}right).$

Используя матрицы, СЛАУ можно переписать в виде $Acdot X=B$. Такую запись часто называют матричным уравнением.

Вообще говоря, в матричном виде записать можно любую СЛАУ.

Примеры решения системы с помощью обратной матрицы

«Решение систем линейных уравнений матричным методом» 👇

Если матрица системы имеет определитель, не равный нулю, то данная система имеет единственное решение, которое можно найти матричным способом.

Если матрица системы имеет определитель, равный нулю, то данную систему нельзя решить матричным способом.

Содержание:

• Матричный метод решения
• Примеры решения систем уравнений

Матричный метод решения

Запишем заданную систему в матричном виде:

$$AX=B$$

Если матрица $$A$$ невырождена, то тогда с помощью
операций над матрицами
выразим неизвестную матрицу $$X$$ . Операция деления на множестве
матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу $A^{-1}$ слева:

$$A^{-1} A X=A^{-1} B Rightarrow E X=A^{-1} B Rightarrow$$
$$X=A^{-1} B$$

Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу
к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.

Примеры решения систем уравнений

Читать дальше: метод Крамера.

Уважаемые студенты,

каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке

Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.

Матричный способ решения СЛУ.

Одним из способов решения СЛУ является матричный способ. Этот способ решения СЛУ применим только при выполнении двух условий:

• Число уравнений равно числу неизвестных;
• Определитель матрицы коэффициентов при неизвестных отличен от нуля.

Теорема (матричный способ решения) Пусть дана система n линейных уравнений с n неизвестными, определитель матрицы коэффициентов А которой отличен от нуля. Тогда решение этой системы может быть получено в виде Х=А^-1В, где В – матрица свободных членов, Х— матрица неизвестных.

ПРИМЕР:

РЕШЕНИЕ:

Запишем матрицу коэффициентов А, матрицу-столбец Х (матрица-столбец неизвестных) и матрицу-столбец В (матрица-столбец свободных членов):

Теперь данную систему можно записать в таком виде АХ=В. Решим это матричное уравнение: Х=А^-1В.

Как найдена матрица А^-1 можно посмотреть здесь.

Таким образом, x=1, y=1, z=1.

ПРОВЕРКА:

Подставим в систему вместо x единицу, y единицу и z единицу.

Верно. Записываем ответ.

ОТВЕТ: (1,1,1).

Упражнения к уроку:

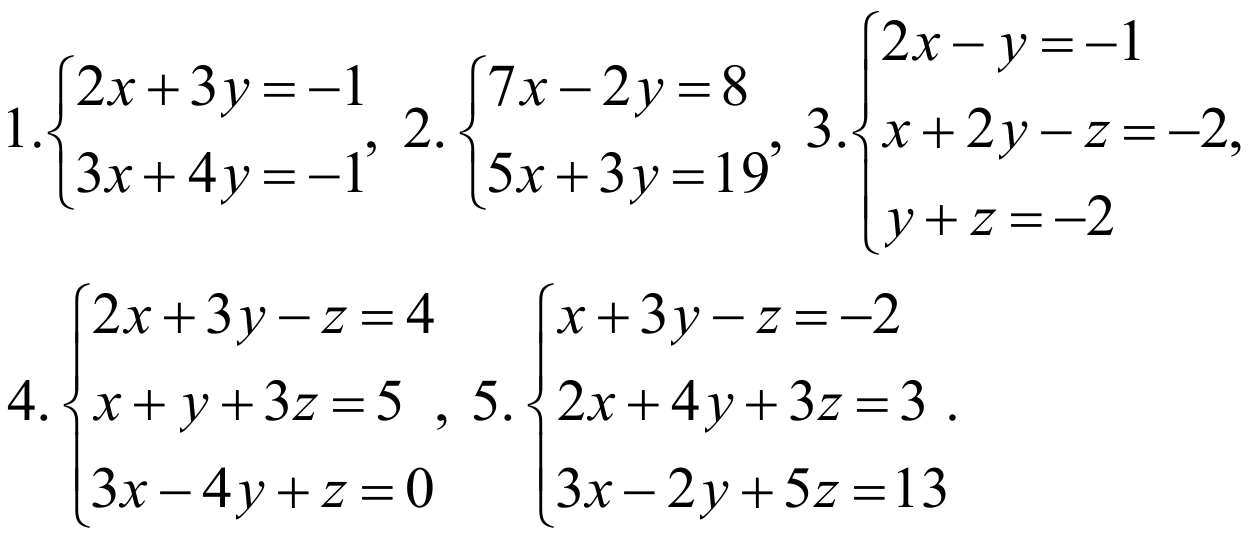
Показать ответ