Как найти сторону через медиану в треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

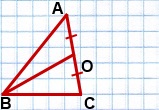
Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Задача

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

Дано: ∆ ABC,

AB=8 см,

BC=6 см,

BO — медиана, BO=√46 см.

Найти: AC.

Решение:

1) На луче BO отложим отрезок OD,

OD=BO.

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

4) По свойству диагоналей параллелограмма,

$[A{C^2} + B{D^2} = 2(A{B^2} + B{C^2})]$

$[A{C^2} + {(2sqrt {46} )^2} = 2({8^2} + {6^2})]$

$[A{C^2} + 184 = 200]$

$[A{C^2} = 16]$

Ответ: 4 см.

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

$[{(2{m_b})^2} + {b^2} = 2({a^2} + {c^2})]$

$[4m_b^2 = 2({a^2} + {c^2}) - {b^2}]$

$[m_b^2 = frac{{2{a^2} + 2{c^2} - {b^2}}}{4}]$

$[{{m_b} = frac{{sqrt {2{a^2} + 2{c^2} - {b^2}} }}{2}}]$

Источник

Узнать ещё

Знание — сила. Познавательная информация

По сторонам и медиане найти сторону треугольника

Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.

По двум сторонам и медиане найти третью сторону треугольника — задача, обратная нахождению медианы треугольника по трем его сторонам .

Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.

Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.

На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.

Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.

Переходим к решению конкретной задачи.

По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.

Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.

Найти сторону треугольника через медиану и стороны

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

BO — медиана, BO=√46 см.

1) На луче BO отложим отрезок OD,

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Определение и свойства медианы равностороннего треугольника

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

ABC

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S₁ = S₂.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

r – радиус вписанной окружности;
R – радиус описанной окружности;
R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

BG = 8 см (самая большая сторона, является гипотенузой △BFG);
FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

источники:

Найти сторону треугольника через медиану и стороны

Определение и свойства медианы равностороннего треугольника

Источник

Как найти сторону треугольника, если известна его медиана и сторона

Информации о медиане и одной из сторон треугольника достаточно для нахождения его другой стороны, если он равносторонний или равнобедренный. В остальных случаях для этого необходимо знать угол между медианой и высотой.

Инструкция

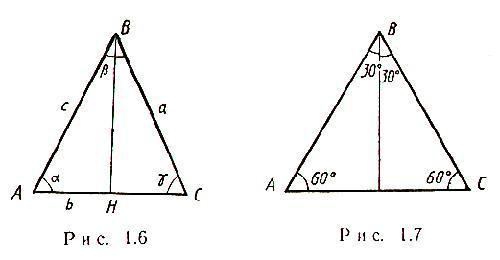
Наиболее простой случай возникает, когда в условии задачи дан равнобедренный треугольник с некоторой стороной a. Две боковые стороны такого треугольника равны, а все медианы пересекаются в одной точке. Кроме того, медиана в равнобедренном треугольнике, проведенная к основанию, является и высотой, и биссектрисой. Соответственно, в треугольнике ABC возникнет треугольник BHC, и по теореме Пифагора можно будет вычислить HC — половину стороны AC:HC=√[(CB)^2-(BH)^2]Следовательно, AC=2√[(CB)^2-(BH)^2]В равнобедренном треугольнике угол α=γ, как это показано на рисунке.

Если в условии задачи приведено значение длины медианы равнобедренного треугольника, проведенной к его боковой стороне, решайте задачу несколько иным способом. Во-первых, медиана не перпендикулярна к боковой стороне фигуры, а во-вторых, формула зависимости между медианой и тремя сторонами выглядит следующим образом:ma=√2(c^2+b^2)-a^2По этой формуле найдите ту сторону, которую медиана делит пополам.

Если треугольник является неправильным, то информации о медиане и стороне недостаточно. Необходимо знать также угол между медианой и стороной. Чтобы решить задачу, вначале найдите по теореме косинусов половину стороны треугольника:c^2=a^2+b^2-2ab*cosγ, где c — сторона, которую нужно найти.Если получается так, что используя теорему косинусов, можно найти лишь только половину стороны, то тогда вычисляемое значение умножается на два. Например, дана медиана и прилежащая к ней сторона, между которыми находится угол. Противоположная углу сторона делится медианой пополам. Вычислив половину стороны по теореме косинусов, получим:BC = 2c, где c — 1/2 стороны BC

Решение прямоугольных треугольников является таким же, как и у любого неправильного треугольника, если нам не известны его углы, а дан лишь только угол между медианой и стороной. Узнав вторую сторону, уже можно найти и третью по теореме Пифагора. Такие задачи помогают искать помимо сторон и другие параметры треугольников. К ним относятся, например, площадь и периметр, которые вычисляются по заданным сторонам и углам.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c — стороны произвольного треугольника

α, β, γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), (a):

Есть следующие формулы для определения катета или гипотенузы

a, b — катеты

c — гипотенуза

α, β — острые углы

Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):

Формулы сторон по теореме Пифагора, (a,b):

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b):

Формулы длины равных сторон , (a):

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β, γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

H — высота из прямого угла

a, b — катеты

с — гипотенуза

c₁, c₂ — отрезки полученные от деления гипотенузы, высотой

α, β — углы при гипотенузе

Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

L— биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L — биссектриса, отрезок ME , исходящий из острого угла

a, b — катеты прямоугольного треугольника

с — гипотенуза

α, β — углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, (L):

Формула длины биссектрисы через катет и гипотенузу, (L):

L — высота = биссектриса = медиана

a — одинаковые стороны треугольника

b — основание

α — равные углы при основании

β — угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

Формула высоты, биссектрисы и медианы, через стороны, (L):

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Источник

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

Найти все стороны треугольника.
Найти все углы треугольника.
Найти площадь (S) и периметр (P) треугольника.
Найти радиус (r) вписанной окружности.
Найти радиус (R) описанной окружности.
Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.

Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.