Как найти сторону через синус формула

Найти сторону треугольника через синус

Неверно введено число.

Неверно задан треугольник.

Стороны треугольника: теорема синусов

Введите стороны треугольника :

a	=
β	=	— в градусах
γ	=	— в градусах

Количество знаков после разделителя дроби в числах:

Теория

Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.

Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника. Например пусть известны сторона a и углы γ и β. С учетом того, что сумма всех углов треугольника равна 180 градусов, угол α будет равен:

Тогда остальные стороны вычисляются по следующим формулам:

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

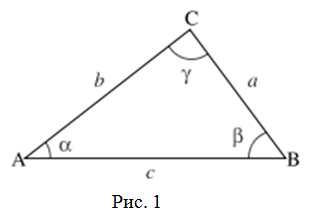
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Формул для нахождения стороны треугольника не так уж много, но главное не знать их — а успешно применять при решении задач, ведь далеко не каждую задачу можно решить в лоб.

Сейчас на примере я покажу, как нужно их применять.

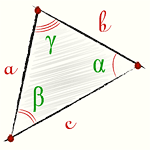
Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок

Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.

Исходя из формулы площади, найдем высоту

S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см

Теперь находим сторону b по синусу угла

sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.

Мы уже знаем две стороны у угол между ними и третью сторону можно найти по формуле из теоремы косинусов, но к сожалению не всегда мы ее помним. В нашем случае ничего страшного — найдем сторону а по формуле Пифагора, но для начала нам нужно найти сторону х.

Можно по формуле Пифагора

откуда х = квадратный корень из (8*8 — 4*4), что равно 4*(кв.к3)

и находим последнюю сторону нашего треугольника

а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4

здесь стоит обратить внимание, что

18*18 = с*с

4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b

2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать

а = кв.к из с*с — 2*с*b*cos30 + b*b Что на самом деле есть формулой нахождения стороны треугольника по теореме косинусов (мы ее только что вывели)

Теперь посчитаем и найдем сторону а = 11,772 см.

Теорема синусов

Теорема синусов гласит

Стороны треугольника пропорциональны синусам противолежащих углов

[
frac{a}{sin(α)} = frac{b}{sin(β)} = frac{c}{sin(γ)}
]

Также отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

[
frac{a}{sin(α)} = frac{b}{sin(β)} = frac{c}{sin(γ)} = 2R
]

Вычислить, найти сторону треугольника по теореме синусов

Пусть известно: две стороны a, b и угол между ними γ. Нужно найти сторону c и недостающие углы α и β. Используем то, что сумма углов треугольника 180°

[
β = (180° — (α + γ))
]

[
frac{a}{sin(α)} = frac{b}{sin(180° — (α + γ))}
]

По формулам приведения

[
sin(180° — (α + γ)) = sin(α + γ)
]

Подставим в (4)

[
frac{a}{sin(α)} = frac{b}{sin(α + γ)}
]

по формуле синуса суммы углов разделим углы

[
sin(α + γ) = sin(α)cos(γ) + cos(α)sin(γ)
]

Получим

[
frac{b}{a} = frac{sin(α)cos(γ) + cos(α)sin(γ)}{sin(α)}
]

[
frac{b}{a} = cos(γ) + ctg(α)sin(γ)
]

Отсюда найдутся все углы треугольника α и β (см. формула (3)):

[
ctg(α) = frac{Largefrac{b}{a}normalsize — cos(γ)}{sin(γ)}
]

Далее теорема синусов позволит найти оставшуюся сторону c

[
с = bfrac{sin(γ)}{sin(β)} = afrac{sin(γ)}{sin(α)}
]

Вычислить, найти две стороны треугольника по теореме синусов

Пусть известно: одна сторона с, и два прилегающих к ней угла α и β. Нужно найти угол γ и стороны a и b. Используем то, что сумма углов треугольника 180°

[
γ = (180° — (α + β))
]

Теперь когда все углы треугольника известны, а также известна одна сторона, теорема синусов позволит легко найти недостающие стороны:

[
a = c frac{sin(α)}{sin(γ)}
]

[
b = c frac{sin(β)}{sin(γ)}
]

Теорема синусов	стр. 238

Содержание:

• Формулировка теоремы синусов
• Расширенная теорема синусов
• Примеры решения задач
• Историческая справка

Формулировка теоремы синусов

Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.

Расширенная теорема синусов

Здесь $R$ — радиус окружности, описанной около рассматриваемого треугольника.

Примеры решения задач

Историческая справка

Самое древнее доказательство для теоремы синусов на плоскости описано в книге «Трактат о полном четырёхстороннике» персидского математика,
механика и астронома Насира ад-Дина Ат-Туси (1201 — 1274), которая была написана в 13 веке. Теорема синусов для сферического треугольника
была доказана математиками средневекового Востока ещё в 10 веке. В труде западноарабского математика, астронома и законоведа
Ал-Джайяни (989 — 1050) 11 века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.