Как найти сторону через треугольника через cos - Исправление недочетов и поиск решений вместе с Examum.ru

Треугольник. Расчет сторон прямоугольного треугольника через тригонометрические функции.

Проанализируем прямоугольный треугольник ABC в котором обозначим катеты как а, b и гипотенузу как с соответственно.

Вполне логично сделать вывод, будут верны следующие равенства:

Значит катет прямоугольного треугольника допускается представить как произведение гипотенузы и синуса угла, противолежащего этому катету, либо и косинуса угла, прилежащего к нему.

На основе этих соотношений так же можно определить гипотенузу прямоугольного треугольника:

Иначе говоря, гипотенуза будет частным от деления катета либо на синус противолежащего к нему угла, либо на косинус прилежащего к катету угла.

Значит, катет прямоугольного треугольника допускается представить как произведением другого катета на тангенс угла, противолежащего первому катету, либо на котангенс угла, прилежащего к первому катету.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α	sin β	sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

источники:

http://www-formula.ru/2011-10-09-11-08-41

http://ru.onlinemschool.com/math/formula/triangle/

Источник

Теорема косинусов

Определение теоремы косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

a²=b²+c²-2*b*c*cos(A)

b²=a²+c²-2*a*c*cos(B)

c²=a²+b²-2*a*b*cos(C)

Расчёт стороны по теореме косинусов

Введите сторону

Введите угол

Формула расчёта стороны по теореме косинусов

Где a, b и c — стороны треугольника,
A — угол между сторонами b и c

Расчёт углов треугольника по теореме косинусов

Введите сторону a

a =

Введите сторону b

b =

Введите сторону c

c =

Формулы расчёта углов по теореме косинусов

Где a, b и c — стороны треугольника,
A, B и C — углы треугольника

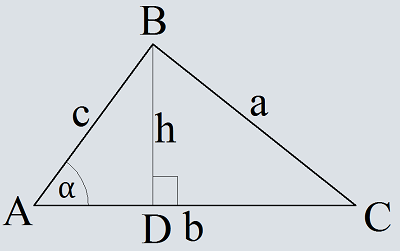
Доказательство теоремы косинусов

Дано

Треугольник со сторонами a, b и c.

Доказать

a²=b²+c²-2*b*c*cos(α)

Доказательство

Из вершины B проведём высоту h

Сравним и упростим

Теорема доказана

Источник

Загрузить PDF

Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ .

1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.^[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — неизвестная сторона, — косинус угла, противоположного неизвестной стороне, и — две известные стороны.^[2]
3
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку . Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.^[4] Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.
- Например, косинус 89° ≈ 0,01745. Итак: $c^{{2}}=5^{{2}}+9^{{2}}-2(5)(9)(0,01745)$ .
5

Перемножьте числа. Умножьте на косинус известного угла.
6

Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
7

Вычтите два числа. Вы найдете $c^{{2}}$ .
8

Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.^[5]

Реклама

1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.^[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — косинус неизвестного угла, — известная сторона, противолежащая неизвестному углу, и — две другие известные стороны. ^[7]
3
4
Перемножьте числа. Умножьте на косинус неизвестного угла.
- Например, $12^{{2}}=8^{{2}}+10^{{2}}-160cos {C}$ .
5
Возведите в квадрат. То есть умножьте число само себя.
- Например, $144=8^{{2}}+10^{{2}}-160cos {C}$
6

Сложите квадраты и . Но сначала возведите соответствующие числа в квадрат.
7

Изолируйте косинус неизвестного угла. Для этого вычтите сумму $a^{{2}}$ и $b^{{2}}$ из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.^[9] На калькуляторе функция арккосинуса обозначается $COS^{{-1}}$ .
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама

1

Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
2

Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
3

Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.

Реклама

Советы

Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.

Об этой статье

Эту страницу просматривали 5444 раза.

Была ли эта статья полезной?

Источник

Как по косинусу найти сторону треугольника

Знание значения косинуса угла в вершине произвольного треугольника позволяет найти величину этого угла. Но по единственному параметру невозможно узнать длину стороны такой фигуры, нужны какие-либо дополнительные связанные с ней величины. Если они даны в условиях, выбор формулы вычисления будет зависеть от того, какие именно параметры выбраны в качестве дополнения к косинусу угла.

Инструкция

Если кроме значения косинуса угла известны длины пары сторон (b и c), которые образуют этот угол, для вычисления величины неизвестной стороны (a) можно использовать теорему косинусов. Она утверждает, что квадрат длины нужной стороны будет равен сумме квадратов длин двух других, если ее уменьшить на удвоенное произведение длин этих же сторон на известный из условий косинус угла между ними: a² = b² + c² — 2*a*b*cos(α).

Поскольку величина угла α вам неизвестна и вычислять ее нет необходимости, обозначьте данную в условиях переменную (косинус угла) какой-либо буквой (например, f) и подставьте в формулу: a² = b² + c² — 2*a*b*f. Избавьтесь от степени в левой части выражения, чтобы получить в общем виде окончательную формулу вычисления длины искомой стороны: a = √(b²+c²-2*a*b*f).

Чтобы найти длину стороны (a), при условии, что кроме значения косинуса (f = cos(α)) лежащего напротив этой стороны угла, дана величина другого угла (β) и длина лежащей напротив нее стороны (b), можно использовать теорему синусов. Согласно ей отношение искомой длины к синусу противолежащего угла равно отношению длины известной стороны к синусу угла, который тоже дан в условиях: a/sin(a) = b/sin(β).

Сумма квадратов синуса и косинуса одного и того же угла равна единице — используйте это тождество, чтобы выразить синус в левой части равенства через заданный в условиях косинус: a/√(1-f²) = b/sin(β). Составьте формулу вычисления длины нужной стороны в общем виде, перенеся знаменатель дроби из левой части тождества в правую: a = √(1-f²)*b/sin(β).

В прямоугольном треугольнике для вычисления величин сторон достаточно дополнить косинус острого угла (f = cos(α)) одним параметром — длиной какой-либо из сторон. Чтобы найти длину катета (b), примыкающего к вершине, косинус угла которой известен, умножьте эту величину на длину гипотенузы (c): b = f*c. Если же нужно вычислить длину гипотенузы, а длина катета известна, трансформируйте эту формулу соответствующим образом: c = b/f.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Теорема косинусов

Теоремы

Треугольник — геометрическая фигура, обладающая 3-мя сторонами и 3-мя углами между ними. Стороны обычно обозначают малыми буквами, совпадающими с обозначениями лежащих напротив вершин. Стороны данной фигуры можно вычислить несколькими способами, в зависимости от исходных данных. Так, одну из сторон треугольника можно рассчитать по теореме косинусов, если известны две другие и угол между ними. Согласно нее квадрат одной его стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: где, a, b, с — стороны, α — угол, лежащий напротив стороны а.

Для расчета стороны треугольника извлекаем корень квадратный из суммы квадратов других сторон минус удвоенное произведение этих сторон на cos угла между ними: Теоремой косинусов можно воспользоваться для расчета косинуса угла треугольника: Т.е. косинус угла равен сумме квадратов двух сторон минус квадрат стороны, противолежащий углу, и все это деленное на удвоенное произведение первых двух сторон. Величину угла находим с помощью тригонометрической таблицы.
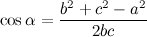
Заметим, если b² + c² — a² больше 0, то угол острый; если меньше 0 — тупой; если равен 0 — прямой.

Найти сторону треугольника по теореме косинусов

Источник