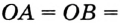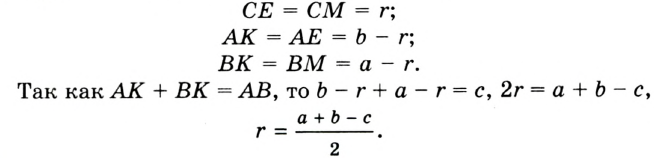Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Длина стороны правильного многоугольника
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Как найти сторону описанной окружности
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
Содержание:
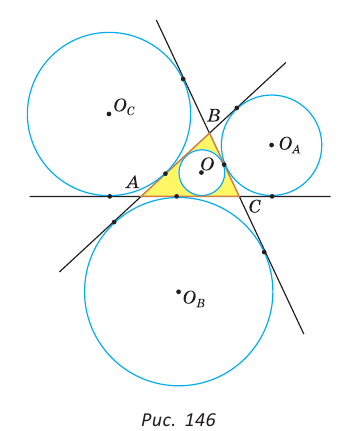
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 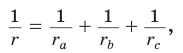
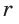
3. 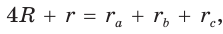
Попробуйте доказать некоторые из этих свойств.
Найдем радиус 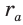
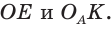
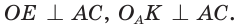
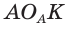
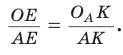
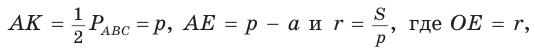
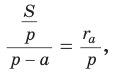
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
Описанная и вписанная окружности треугольника
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
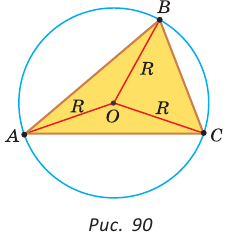
На рисунке 90 изображена окружность с радиусом R и центром 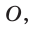
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
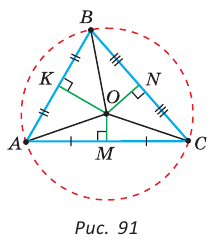
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
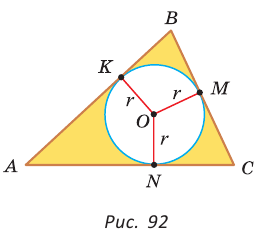
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
На рисунке 92 изображена окружность с центром О и радиусом 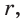
Так как 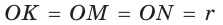
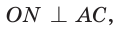
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
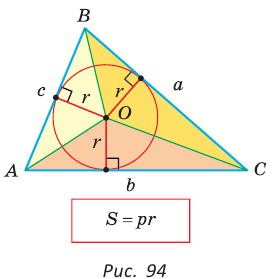
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
Теорема. Площадь треугольника можно найти по формуле 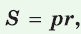
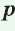
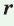
Пусть дан треугольник АВС со сторонами 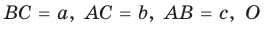
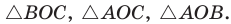
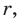
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
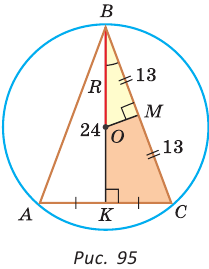
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 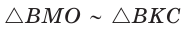
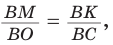
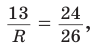
Способ 2 (тригонометрический метод). Из 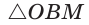
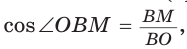
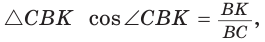
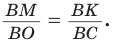
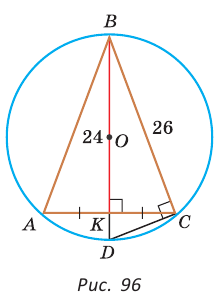
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 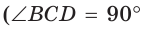
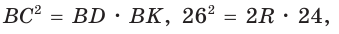
Ответ: 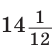
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 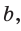
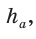
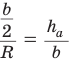
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
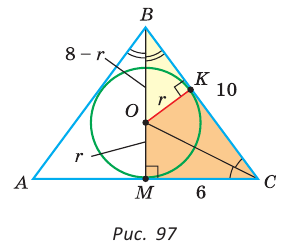
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 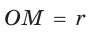
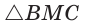
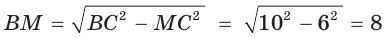
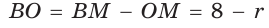
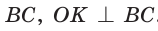
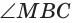
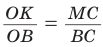
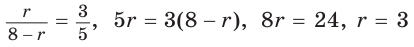
Способ 2 (тригонометрический метод). Из 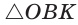
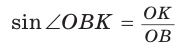
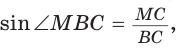
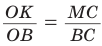
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 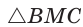
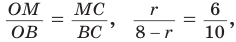
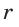
Способ 4 (формула 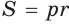
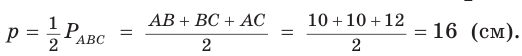
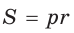
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 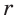
Решение:
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
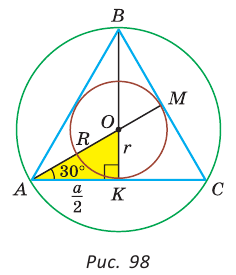
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 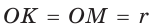
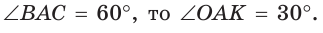
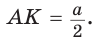
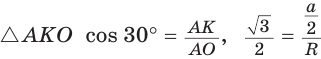
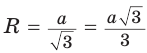
В 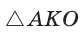
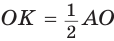
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 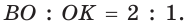
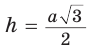
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника 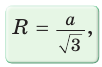
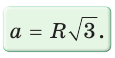
треугольника в 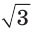
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 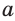
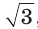
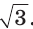
Прямоугольный треугольник и его описанная и вписанная окружности
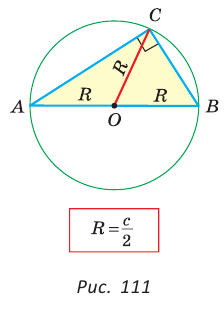
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 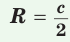
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 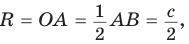
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
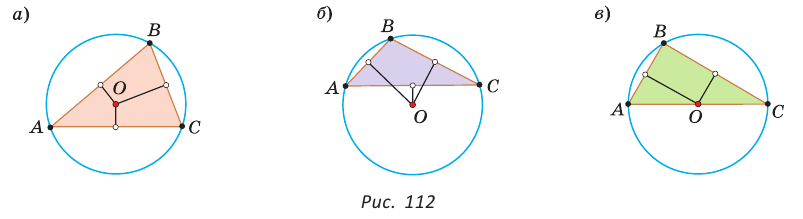
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
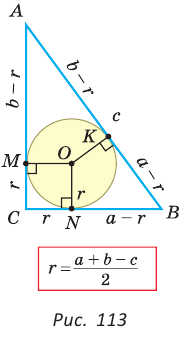
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 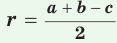
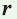
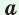
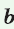
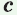
Рассмотрим прямоугольный треугольник АВС с катетами 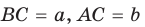
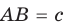
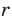
Проведем радиусы в точки касания и получим: 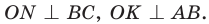
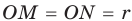
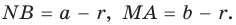
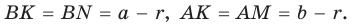
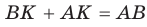
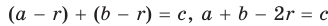
Следствие: 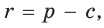
Преобразуем формулу радиуса вписанной окружности:
Формула 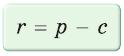
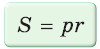
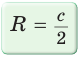
Пример. Дан прямоугольный треугольник, 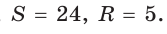
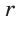
Решение:
Так как 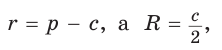
Из формулы 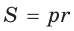
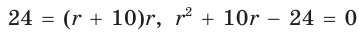
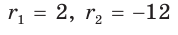
Ответ: 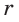
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
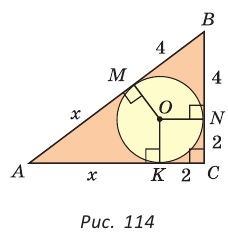
Способ 1 (геометрический). Пусть в треугольнике АВС, где 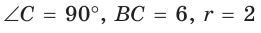
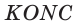
По свойству касательных
Тогда 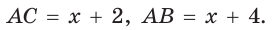
Следовательно,
Радиус описанной окружности
Способ 2 (алгебраический). Подставив в формулу 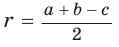
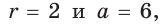
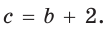
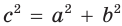
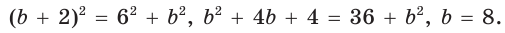
Ответ: 5.
Пример:
Гипотенуза прямоугольного треугольника 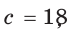
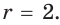
Решение:
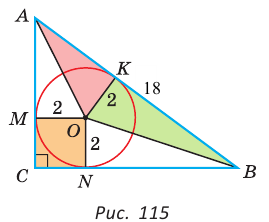
Способ 1 (геометрический). Пусть в 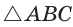
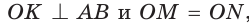
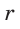
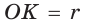
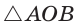
Отсюда 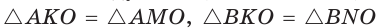
Площадь 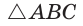
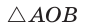
Способ 2 (алгебраический). Из формулы 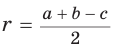
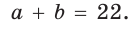
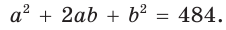
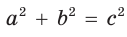
Способ 3 (алгебраический). Из формулы 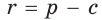
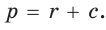
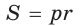
Ответ: 40.
Реальная геометрия:
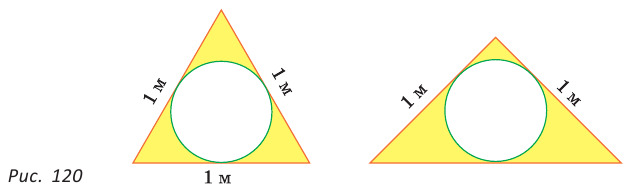
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
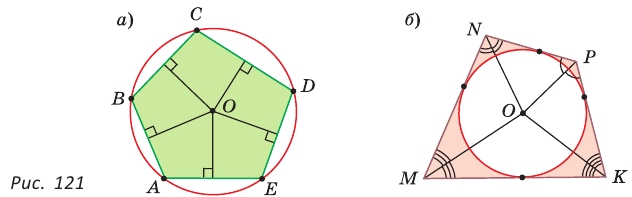
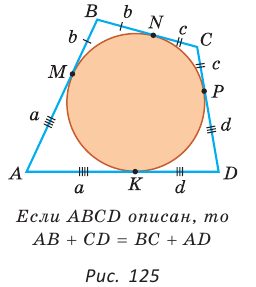
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
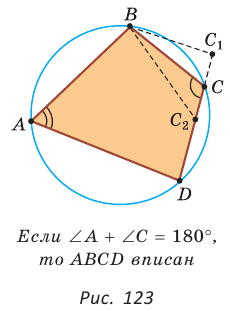
Теорема (свойство вписанного четырехугольника).
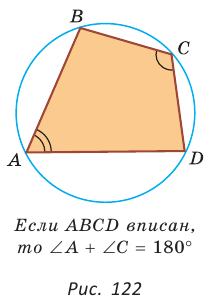
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 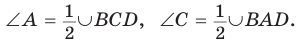
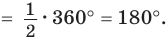
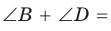
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна 
Рассмотрим четырехугольник ABCD, у которого 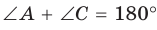
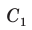
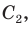
Тогда сумма 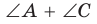
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
Следствия.
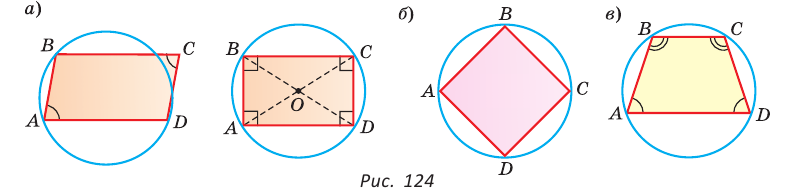
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Пусть для выпуклого четырехугольника ABCD справедливо, что
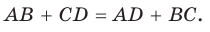
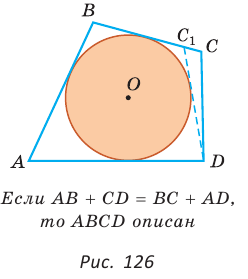
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 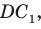
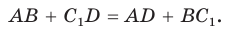
Отняв почленно от равенства (1) равенство (2), получим 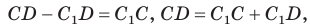
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
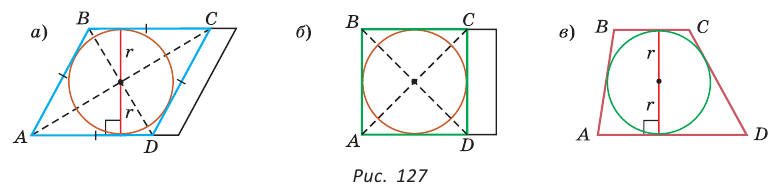
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
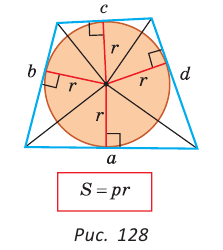
Для описанного многоугольника справедлива формула 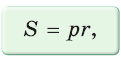
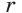
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
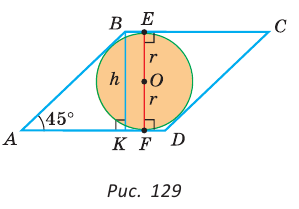
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 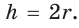
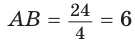
Из прямоугольного треугольника АВК находим. что 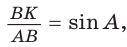
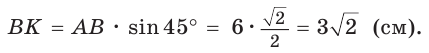
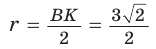
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 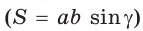
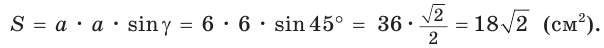
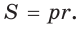
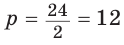
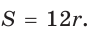
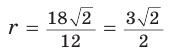
Ответ: 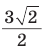
Пример:
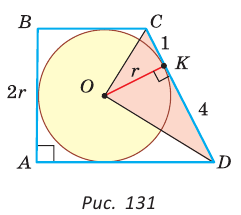
Окружность, вписанная в прямоугольную трапецию ABCD, где 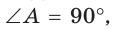
Решение:
Способ 1. Площадь трапеции находится по формуле 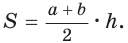
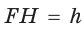
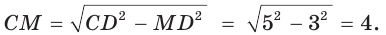
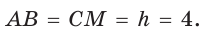
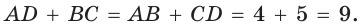
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов 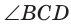
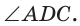
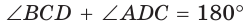
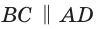
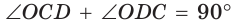
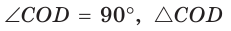
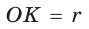
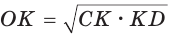
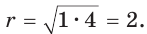
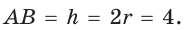
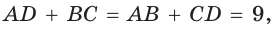
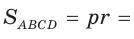
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
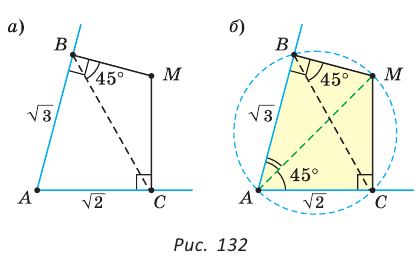
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 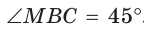
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 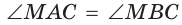
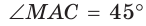
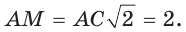
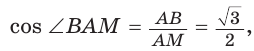
Окружность, вписанная в треугольник
Пример:
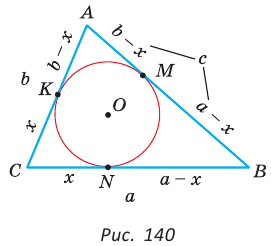
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
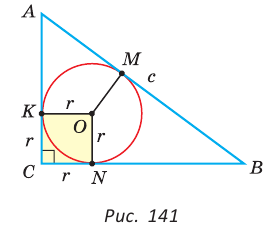
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 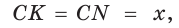
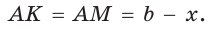
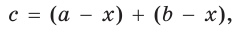
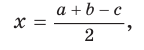
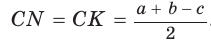
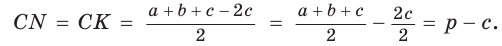
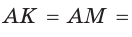
Ответ:
Замечание. Если 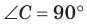
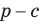
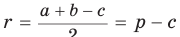
Описанная трапеция
Пример:
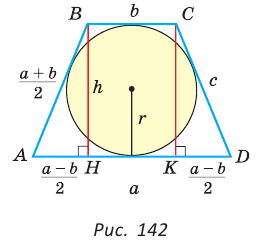
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле 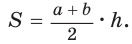
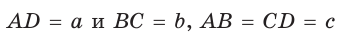
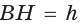
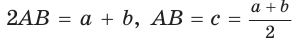
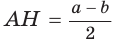
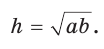
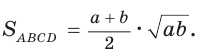
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 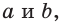
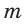
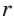
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
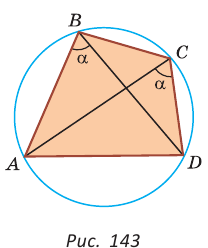
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 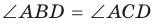
2. Докажем, что если в некотором четырехугольнике ABCD 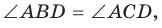
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 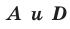
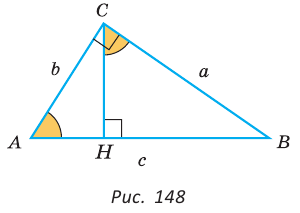
Обобщенная теорема Пифагора
В прямоугольном треугольнике 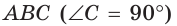
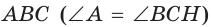
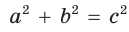
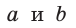
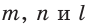
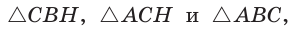
Действительно, из подобия указанных треугольников 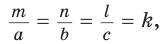
Пример:
Пусть 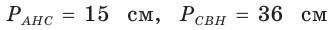
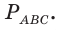
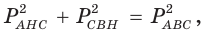
Ответ: 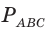
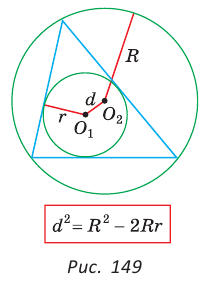
Формула Эйлера для окружностей
Для вписанной и описанной окружностей треугольника с радиусами 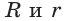
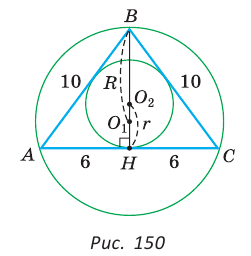
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 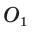
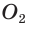
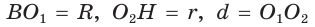
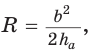
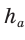
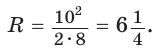
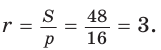
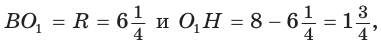
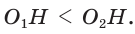
А теперь найдем d по формуле Эйлера:
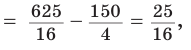
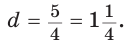
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле
где
— полупериметр,
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
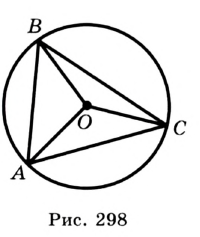
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 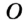
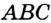
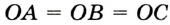
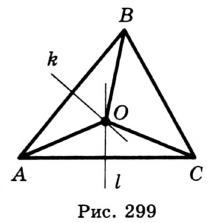
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 
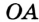
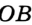
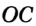
На рисунке 299 изображен произвольный треугольник 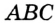
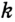
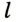
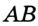
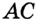
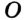

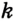
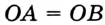
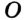
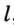
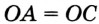
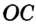

Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 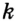
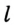
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка 
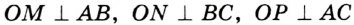
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 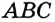
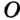
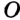
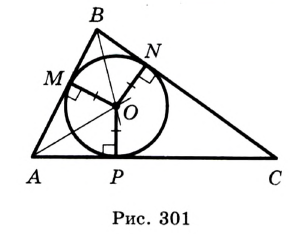
На рисунке 301 изображен произвольный треугольник 




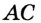


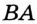
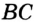

Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов 

Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
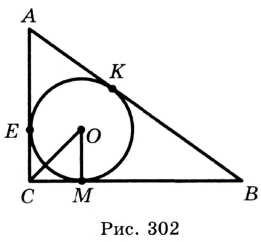
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 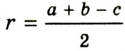
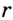
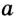
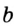
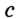
Решение:
В треугольнике 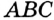
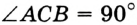
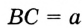
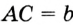
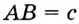
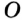
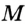
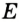
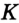
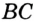
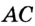
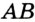
Отрезок 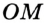
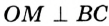
Так как точка 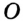
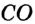
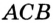
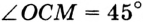
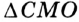
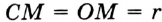
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://planetcalc.ru/92/
http://b4.cooksy.ru/articles/kak-nayti-storonu-opisannoy-okruzhnosti
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
-
Расчет длины стороны
- Через радиус вписанной окружности
- Через радиус описанной окружности
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Через радиус вписанной окружности
Формула расчета
Через радиус описанной окружности
Формула расчета
Да почти так же, как и ВПИСАННОГО.
Обозначим радиус окружности R, количество сторон правильного многоугольника n, и длину стороны а.
К обоим концам одной из сторон многоугольника из центра окружности проведём лучи. Получится центральный угол равный (360/n)°. Эти проведённые радиусы и сама сторона образуют равнобедренный треугольник. Из центра окружности проведём высоту этого равнобедренного треугольника, (она равна радиусу) которая разбивает его на два прямоугольных треугольника, с длинным катетом R, коротким катетом а/2 и острым углом против него, равным (180/n)°. Из любого из этих треугольников получаем a/2=R*tg(180/n).
Ну и, умножая на 2, получаем a=2*R*tg(180/n).
Вписанные и описанные четырехугольники
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
Рассмотрим теоремы о вписанных и описанных четырехугольниках и их свойствах.
Теорема 1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны
Теорема 2. Четырёхугольник можно описать вокруг окружности тогда и только тогда, когда суммы его противоположных сторон равны.
Теорема 3. Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.
Теорема 4. (Птолемея). Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Теорема 5. Площадь описанного четырехугольника равна произведению полупериметра четырёхугольника на радиус вписанной в него окружности.
Теорема 6. Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Теорема 7. Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Теорема 8. Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Теорема 9. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 10. В любой ромб можно вписать окружность.
Теорема 11. В любой квадрат можно вписать окружность.
Теорема 12. В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом.
Теорема 13. В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Теорема 14. В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований.
Посмотрим, как эти свойства применяются в решении задач ЕГЭ.
Задача 1. Два угла вписанного в окружность четырехугольника равны и
. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна . Пусть угол
равен
. Тогда напротив него лежит угол в
градусов. Если угол
равен
, то угол
равен
.
Ответ: 122.
Задача 2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
.
Решение:
Пусть сторона равна
,
равна
, а
. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,
Получается, что равна
. Тогда периметр четырехугольника равен
. Мы получаем, что
, а большая сторона равна
.
Ответ: 12.
Задача 3. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.
Решение:
Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны и
, а боковые стороны —
и
. По свойству описанного четырехугольника,
, и значит, периметр равен
.
Получаем, что , а средняя линия равна
.
Ответ: 10.
Задача 4. Угол A четырехугольника , вписанного в окружность, равен
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Четырехугольник вписан в окружность. Значит, сумма его противоположных углов равна
Поэтому
Ответ: 148.
Задача 5. Углы четырехугольника
относятся как
. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Решение:
Пусть
Сумма всех углов четырехугольника равна
А сумма каждой пары противоположных углов равна (т.к. четырехугольник вписан в окружность).
Запишем эти два условия в виде двух уравнений с двумя неизвестными:
Подставляем второе уравнение в первое и получаем
Ответ: 90.
Задача 6. Стороны четырехугольника
и
стягивают дуги описанной окружности, градусные величины которых равны соответственно
и
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна .
Поэтому
Угол А – вписанный, опирается на дугу , равную сумме дуг
и
, т.е.
Тогда вписанный угол А равен половине дуги , т.е.
Ответ: 107.
Задача 7. Точки расположенные на окружности, делят эту окружность на четыре дуги
и
градусные величины которых относятся соответственно как
Найдите угол A четырехугольника
Ответ дайте в градусах.
Решение:
Угол А – вписанный, опирается на дугу равную сумме дуг
и
Найдем дуги
и
Обозначим градусные величины дуг и
как
согласно заданному соотношению между дугами.
Тогда или
Сумма дуг и
составляет
Вписанный угол А равен половине дуги т.е.
Ответ: 15.
Задача 8. Радиус окружности, описанной около квадрата, равен Найдите длину стороны этого квадрата.
Решение:
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата. Тогда диагональ квадрата равна
Выразим сторону квадрата через его диагональ:
Ответ: 32.
Задача 9. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Решение:
Если правильный шестиугольник вписан в окружность, то радиус окружности равен стороне шестиугольника. Поэтому сторона равна 6.
Ответ: 6.
Задача 10. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Решение:
Поскольку трапеция вписана в окружность, она равнобедренная.
Рассмотрим равнобедренную трапецию с основаниями
Тогда боковые стороны
Проведем параллельно
Тогда треугольник
– равнобедренный, т.к.
и равносторонний, т.к.
Поэтому
– параллелограмм по построению, но
, поэтому
– ромб, и
Получаем, что О – центр описанной окружности с радиусом, равным меньшему основанию –
Ответ: 6.
Задача 11. Найти диагональ параллелограмма, вписанного в окружность радиусом 6 см.
Решение:
Согласно одной из теорем, окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру, см.
Ответ: 12.
Задача 12. Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Поэтому сумма оснований
Сумму боковых сторон найдем как разность между периметром и суммой оснований:
Трапеция вписана в окружность, следовательно, трапеция равнобедренная, боковые стороны равны:
Ответ: 5.
Задача 13. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и
Решение:
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру окружности.
В то же время по теореме Пифагора диагональ найдем как
Радиус окружности равен половине диаметра:
Ответ: 9.
Задача 14. Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение:
Радиус окружности, вписанной в квадрат, равен половине его стороны. Поэтому
Ответ: 8.
Задача 15. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна 11 (половине периметра).
Боковая сторона тогда боковая сторона
Радиус вписанной окружности равен половине т.е. 2.
Ответ: 2.
Задача 16. Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение:
Высота трапеции, в которую вписана окружность, равна диаметру этой окружности:
Ответ: 28.
Задача 17. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна
Средняя линия трапеции равна полусумме оснований
Ответ: 16.
Задача 18. Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 16. Найдите его площадь.
Решение:
Площадь описанного многоугольника можно найти как произведение полупериметра на радиус вписанной окружности:
Ответ: 16.
Задача 19. В равнобедренной трапеции, вписанной в окружность, диагонали взаимно перпендикулярны. Средняя линия трапеции равна 12. Найти радиус вписанной окружности.
Решение:
Радиус окружности, вписанной в трапецию, равен половине ее высоты.
Рассмотрим равнобедренную трапецию
Проведем Треугольник
– прямоугольный (с прямым углом С) и равнобедренный. Его гипотенуза
равна сумме оснований трапеции (т.к.
– параллелограмм, и
),
Высота трапеции является также высотой и медианой, проведенной из прямого угла равнобедренного прямоугольного треугольника
.
Радиус вписанной окружности
Ответ: 6.
Задача 20. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Решение:
Пусть О – центр описанной окружности. Проведем высоту проходящую через точку О. Тогда
(радиусы окружности),
Треугольники и
– прямоугольные. Применяя теорему Пифагора, найдем:
Ответ: 7.
Это были задачи по теме «Вписанные и описанные четырехугольники» из первой части ОГЭ и ЕГЭ. Покажем более сложную задачу, из второй части ОГЭ по математике.
Задача 21. В четырёхугольник можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника перпендикулярны. Найдите его площадь, если радиус описанной окружности равен 5, а
Решение:
Обозначим Тогда
Обозначим также
Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны.
Значит, Отсюда
Пусть О – точка пересечения диагоналей четырёхугольника
При пересечении и
образуется четыре прямоугольных треугольника. Это
Пусть
Запишем для каждого из этих треугольников теорему Пифагора:
Из
Из
Из
Из
Мы получили систему уравнений.
Сложив первое и третье из них и выразив как
получим:
Кроме того, Это мы нашли в самом начале.
Из системы уравнений
находим:
Значит,
Перестроим чертеж. Это надо сделать обязательно. Появились новые данные – рисуем новый чертеж. По условию, четырехугольник вписан в окружность.
Треугольники и
равны по трем сторонам. Значит, углы
и
равны.
Четырехугольник вписан в окружность, поэтому сумма углов
и
равна 180 градусов. Мы получили, что углы
и
– прямые. Тогда
– диаметр окружности.
По условию, , тогда
опирается на диаметр.
– прямоугольный,
– его гипотенуза.
По теореме Пифагора для :
Отсюда
Ответ: 40.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вписанные и описанные четырехугольники» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Содержание
- Определение правильного многоугольника
- Элементы правильного многоугольника
- Диагонали n — угольника
- Внешний угол многоугольника
- Сумма внутренних углов
- Сумма внешних углов
- Виды правильных многоугольников
- Основные свойства правильного многоугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Доказательства свойств углов многоугольника
- Правильный n-угольник — формулы
- Формулы длины стороны правильного n-угольника
- Формула радиуса вписанной окружности правильного n-угольника
- Формула радиуса описанной окружности правильного n-угольника
- Формулы площади правильного n-угольника
- Формула периметра правильного многоугольника:
- Формула определения угла между сторонами правильного многоугольника:
- Формулы правильного треугольника:
- Формулы правильного четырехугольника:
- Формулы правильного шестиугольника:
- Формулы правильного восьмиугольника:
- Сторона правильного многоугольника через радиус описанной вокруг него окружности
- Шаг 1
- Шаг 2
- Шаг 3
Определение правильного многоугольника
Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.
Признаки правильного n-угольника
- a1 = a2 = a3 = … an-1 = an
- α1 = α2 = α3 = … αn-1 = αn
Примечание: n – количество сторон/углов фигуры.
Элементы правильного многоугольника
Для рисунка выше:
- a – сторона/ребро;
- α – угол между смежными сторонами;
- O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
- β – центральный угол описанной окружности, опирающийся на сторону многоугольника.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника |
 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
 |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
 |
Число диагоналейn – угольника равно |
| Диагональ многоугольника |

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |

Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n — 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n — 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.
Виды правильных многоугольников
- Правильный (равносторонний) треугольник
- Правильный четырехугольник (квадрат)
- Правильный пяти-, шести-, n-угольник
Основные свойства правильного многоугольника
- Все стороны равны:
a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:
180° · (n — 2)
- Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
- В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Свойство 1
Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:
где n – число сторон фигуры.
Свойство 2
Сумма всех углов правильного n-угольника равняется: 180° · (n-2).
Свойство 3
Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:
Свойство 4
В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.
В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.
Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:
Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:
Свойство 5
Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:
- Площадь (S):
- Периметр (P):
- Радиус описанной окружности (R):
- Радиус вписанной окружности (r):
Свойство 6
Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов – угольникаn равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов – угольникаn , взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности:
- Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны:
- Формула площади n-угольника через радиус вписанной окружности:
- Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
 |
| Рис.3 |
Формулы правильного треугольника:
- Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
- Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
- Формула радиуса вписанной окружности правильного треугольника через длину стороны:
- Формула радиуса описанной окружности правильного треугольника через длину стороны:
- Формула площади правильного треугольника через длину стороны:
- Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
- Формула площади правильного треугольника через радиус описанной окружности:
- Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Формулы правильного четырехугольника:
- Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
- Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
- Формула площади правильного четырехугольника через длину стороны:
S = a2
- Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
- Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
- Угол между сторонами правильного четырехугольника:
α = 90°
Формулы правильного шестиугольника:
Формула стороны правильного шестиугольника через радиус вписанной окружности:
Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
Формула площади правильного шестиугольника через длину стороны:
Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Формулы правильного восьмиугольника:
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
Угол между сторонами правильного восьмиугольника:
α = 135°
Сторона правильного многоугольника через радиус описанной вокруг него окружности
Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле
Где:
a – длина его стороны;
R – радиус описанной окружности;
n – число сторон многоугольника.
Формула стороны правильного многоугольника
Шаг 1
Рассмотрим правильный многоугольник А1А2А3…Аn.
Пусть его сторона будет равна a.
Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.
Вывод формулы стороны правильного многоугольника.
Шаг 2
Соединим точку О с его вершинами. А1А2А3…Аn.
Рассмотрим треугольник ОА1А2.
Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.
Проведем в треугольнике А1ОА2 высоту ОК.
Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:
Вывод формулы стороны правильного многоугольника.
Шаг 3
Рассмотрим треугольник А1КО.
Этот треугольник прямоугольный, так как ОК – высота по построению.
Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.
Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:
По свойству углов правильного многоугольника, каждый угол равен:
Тогда угол ОА1К будет равен:
Из определения косинуса угла получим:
Отсюда:
Подставим в формулу значения, полученные выше и на шаге 2:
Умножим обе части уравнения на 2:
Воспользуемся формулами приведения
Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:
Вывод формулы стороны правильного многоугольника.



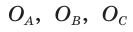
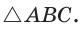
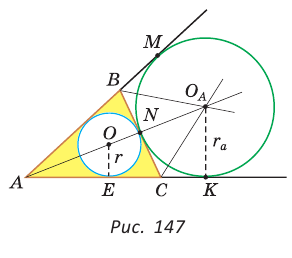
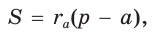
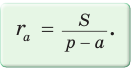
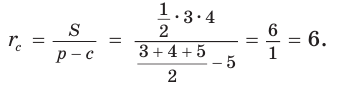
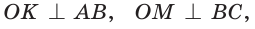
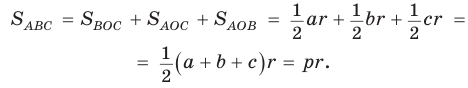
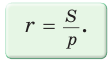
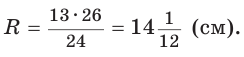
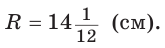
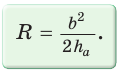
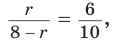
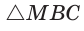
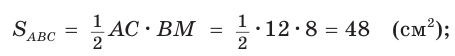
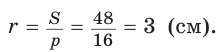
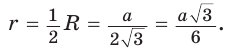
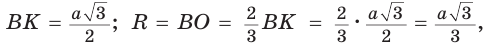
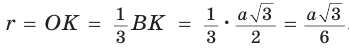
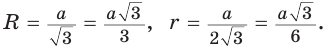
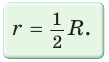
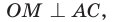
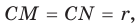
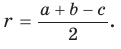
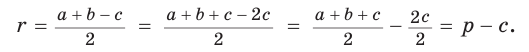
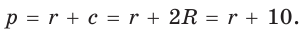
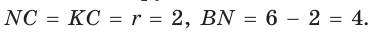
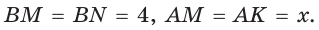
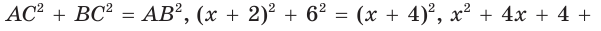
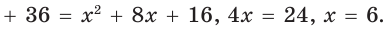
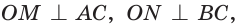
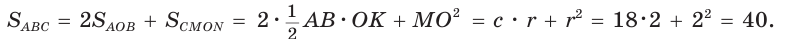
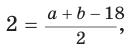
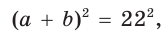
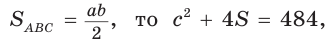
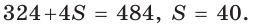
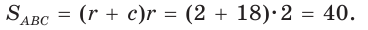
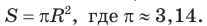

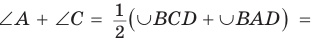
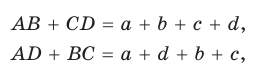
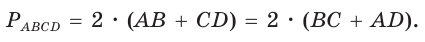
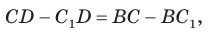
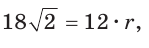
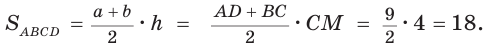
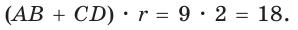
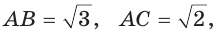
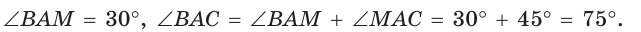
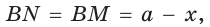
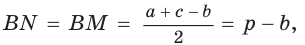
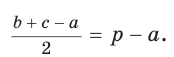
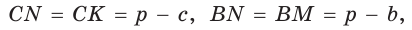
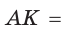
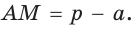
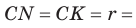
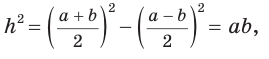
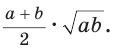
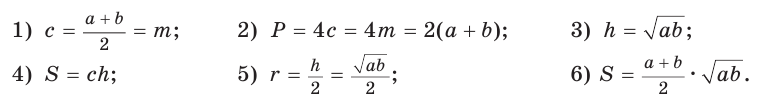
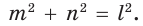
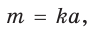
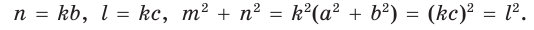
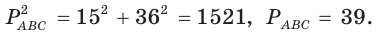
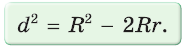
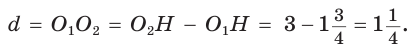
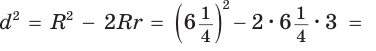
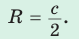
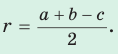
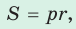 где
где 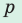 — полупериметр,
— полупериметр, 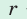 — радиус вписанной окружности.
— радиус вписанной окружности.