как найти ребро куба, если известна диагональ
Светило науки — 9801 ответ — 46531 помощь
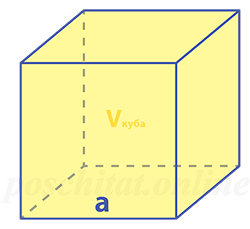
Примем ребро куба за а.
Диагональ d основания равна а√2.
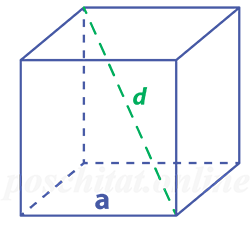
Диагональ D куба — это гипотенуза треугольника, где катеты: диагональ d основания и ребро куба a.
D = √(d²+a²) = √(2a²+a²) = √(3a²) = a√3.
Отсюда получаем: а = D/√3.
Светило науки — 3 ответа — 0 раз оказано помощи
если сторона куба равна х,
диагональ стороны куба равна корень из 2х квадрат.
теперь вычислить диагональ куба — гипотенуза прямоугольного треугольника со сторонами х и уже вычисленной стороной
Как найти сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).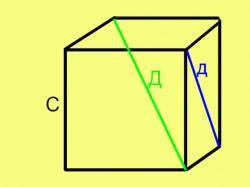
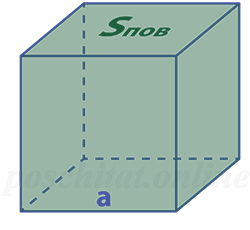
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П — площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ — функция извлечения кубического корня).
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также
Викториныч
20 марта, 19:42
Как найти ребро куба, если известна диагональ
-
Радомира
20 марта, 20:16
0
Если сторона куба равна х,
диагональ стороны куба равна корень из 2 х квадрат.
теперь вычислить диагональ куба — гипотенуза прямоугольного треугольника со сторонами х и уже вычисленной стороной
- Комментировать
- Жалоба
- Ссылка
-
Примем ребро куба за а.
Диагональ d основания равна а√2.
Диагональ D куба — это гипотенуза треугольника, где катеты: д иагональ d основания и ребро куба a.
D = √ (d²+a²) = √ (2a²+a²) = √ (3a²) = a√3.
Отсюда получаем: а = D / √3.
- Комментировать
- Жалоба
- Ссылка
Найдите правильный ответ на вопрос ✅ «Как найти ребро куба, если известна диагональ …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Новые вопросы по математике
Диагональ стороны куба является диагональю квадрата, который представляет собой грань куба. Исходя из этого, ребро куба может быть вычислено по формуле отношения диагонали стороны куба к корню из двух.
a=d/√2
Тогда площадь стороны куба, равная квадрату его ребра, будет рассчитываться как квадрат диагонали, деленный на два. Чтобы вычислить площадь боковой и полной поверхности куба, необходимо умножить полученное выражение на 4 или 6 соответственно.
S=a^2=d^2/2
S_(б.п.)=4a^2=(4d^2)/2=2d^2
S_(п.п.)=6a^2=(6d^2)/2=3d^2
Чтобы вычислить объем куба, нужно возвести его ребро в третью – кубическую – степень, для этого все выражение, полученное для ребра куба через диагональ его стороны, возводится в степень.
V=a^3=(d/√2)^3=d^3/(2√2)
Периметр куба равен ребру куба, умноженному на двенадцать. Подставив вместо ребра куба выражение через диагональ и сократив коэффициенты, получим следующую формулу для периметра:
P=12a=12d/√2=6√2 d
Диагональ куба через диагональ его стороны можно найти, используя теорему Пифагора, согласно которой квадрат диагонали куба равен сумме квадратов диагонали стороны и бокового ребра, соединенных в прямоугольный треугольник. (рис.2.1.)
a^2+d^2=D^2
D^2=d^2/2+d^2
D^2=(3d^2)/2
D=√(3/2) d
Чтобы вычислить радиус сферы, вписанной в куб, необходимо разделить на два ребро куба, то есть разделить на два корня из двух диагональ его стороны. Радиус сферы, описанной вокруг куба, в свою очередь равен половине диагонали куба, вместо которой также можно использовать полученное через диагональ стороны выражение. (рис.2.2.,2.3)
r=a/2=d/(2√2)
R=D/2=(√(3/2) d)/2