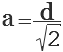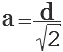Сторона квадрата
Стороны фигур
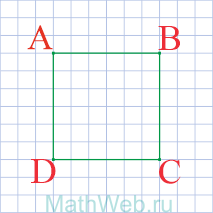
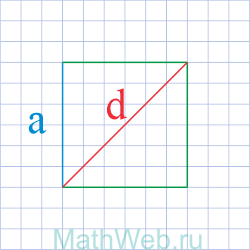
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d2 = а2 + а2 = 2а2.
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Расчет стороны квадрата через диагональ
Расчет стороны квадрата через площадь
/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
532 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
829 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1028 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a2+a2=d2
2a2=d2
Найти стороны квадрата через диагональ поможет теорема Пифагора.
Впрочем, если это квадрат, то нужно искать не стороны квадрата, а одну его сторону, поскольку все стороны равны.
Диагональ делит квадрат на два треугольника, для каждого треугольника (а они — прямоугольные), диагональ является гипотенузой, а стороны квадрата — катетами.
Чтобы не вводить лишние буквенные обозначения я так и обозначу: гипотенузу буквой «г», а сторону квадрата буквой «с».
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
г2 = с2 + с2 (с2 — это с в квадрате, не знаю как записать точнее )
г2 = 2 с2
с2 = г2/2 (г в квадрате, делённое на 2)
с = квадратному корню из г2/2
Г — диагональ квадрата, она известна; подставляем в формулу
Где d — диагональ квадрата.
Где S — площадь квадрата
Где r — радиус вписанной окружности
Где R — радиус описанной окружности
Где P — периметр квадрата.
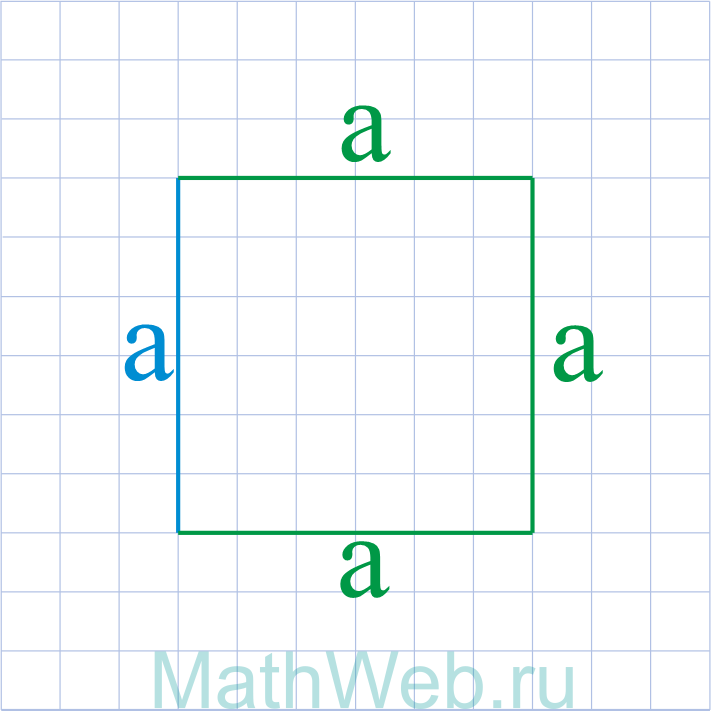
- Квадрат — это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные — перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = |
 |
a = √S |
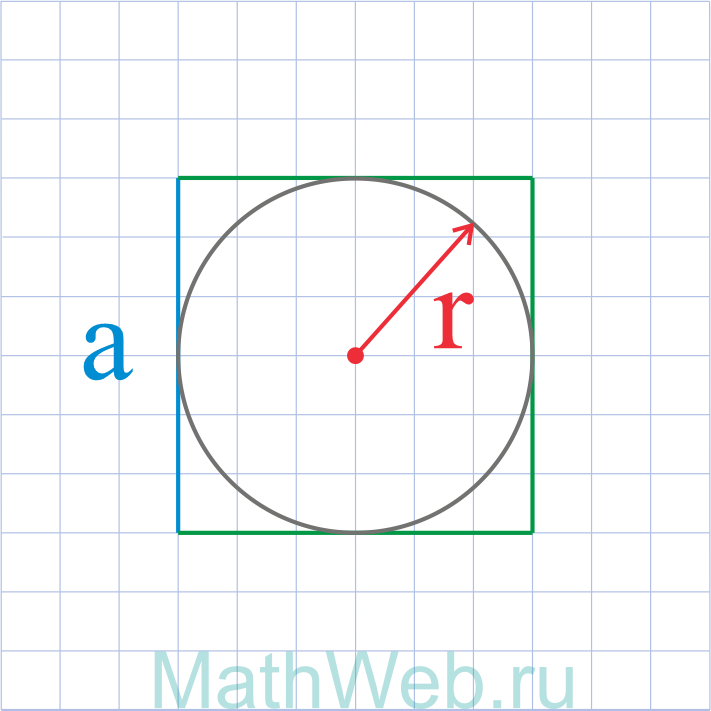 |
a = 2r |
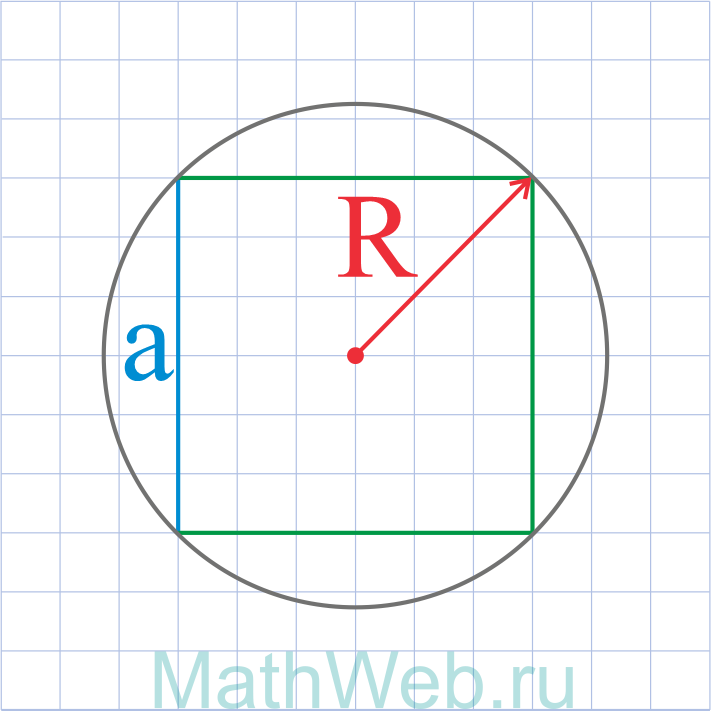 |
a = R√2 |
 |
a = |