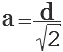/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
532 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
829 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1028 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Квадрат – это четырёхугольная плоская геометрическая фигура с равными сторонами. Квадрат считается
прямоугольником, так как все его внутренние углы по 90°. Диагонали правильного четырёхугольника
равны между собой, пересекаются под прямым углом и делятся точкой пересечения пополам. А также они
являются биссектрисами внутренних углов (отрезок делит прямой угол на два одинаковых угла по 45°).
Знание и применение этих свойств позволяют быстро решать задачи по геометрии. Ромб с равными
диагоналями, ромб с двумя соседними прямыми углами, параллелограмм с одинаковыми диагоналями,
пересекающимися под прямым углом, все эти фигуры являются правильными четырёхугольниками.
- Сторона квадрата через радиус вписанной окружности
- Сторона квадрата через радиус описанной окружности
- Сторона квадрата через площадь квадрата
- Сторона квадрата через диагональ
Через радиус вписанной окружности
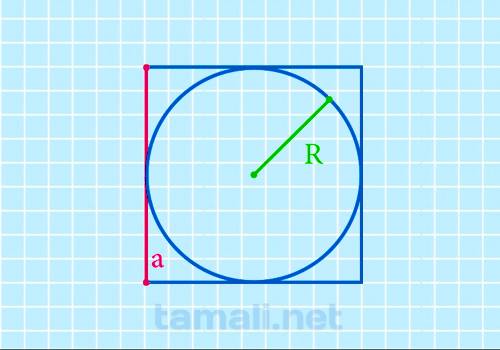
Длина стороны равна двум радиусам (диаметру) вписанной окружности:
a=2*R
где R — радиус.
Цифр после
запятой:
Результат в:
Радиус – это расстояние от центра окружности до любой ее точки. Диаметр — отрезок, соединяющий
две любые точки окружности и проходящий через центр. Радиус составляет 1/2 диаметра. Все стороны
правильного четырёхугольника являются касательными прямыми к вписанной окружности. Радиус всегда
перпендикулярен касательной. Вписанная окружность делит точкой касания стороны квадрата на две
равные части. Зная величину диагонали, одинаковую длину стороны и диаметра легко можно объяснить
благодаря теореме Пифагора: «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов». В данном случае если построить отрезки, соединяющие противоположные вершины правильного
четырёхугольника, образуется равнобедренный прямоугольный треугольник, где половина стороны квадрата
и радиус являются катетами, а половина диагонали — гипотенузой.
Формула вычисления через площадь
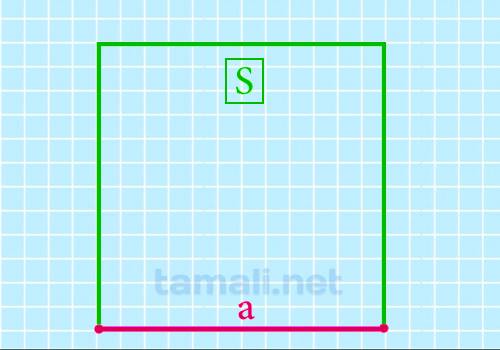
Для того чтобы определить длину стороны, зная только площадь, нужно извлечь квадратный корень из
известного значения:
a=√S
где S — площадь.
Цифр после
запятой:
Результат в:
Это самый простой способ. Площадь плоской четырёхугольной геометрической фигуры – это числовое
значение, которое характеризует размер плоскости, ограниченной четырьмя сторонами. Для нахождения
площади прямоугольника необходимо умножить длину на ширину, для площади прямоугольника с равными
сторонами – возвести длину в квадрат.
Также есть и другие способы для нахождения площади правильной
четырёхугольной фигуры: через радиус вписанной или описанной окружности, периметр, через длину
отрезка, проведенного из вершины к середине противоположной стороны. Если площадь неизвестна, но
есть данные о диагонали, можно легко найти воспользоваться доступной величиной — возвести
длину отрезка в квадрат и разделить на два S=d²/2.
Этот метод также
опирается на теорему Пифагора. Поделив сумму квадратов катетов на два, можно найти площадь. Однако в
этом случае значение не понадобится для нахождения стороны, можно быстро вычислить длину катета при
помощи следующей формулы.
Вычисление через диагональ
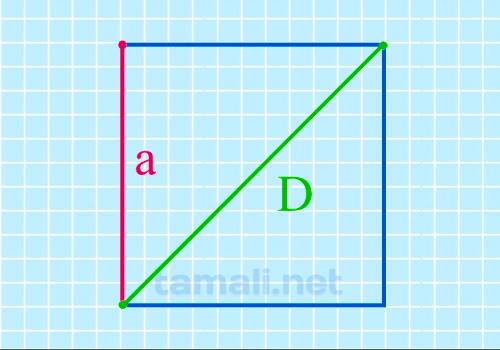
Если в задаче изначально известна длина диагонали, можно значительно сократить маршрут поиска нужной
величины. На основе этого правила сторона вычисляется по формуле:
a=d/√2
где d — диагональ.
Цифр после
запятой:
Результат в:
Через радиус описанной окружности
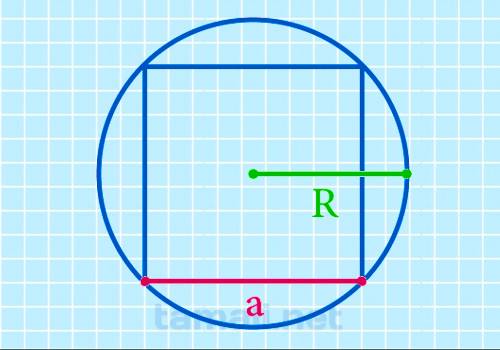
Известно, что диаметр описанной окружности равен диагонали, так как он совпадает с отрезком,
соединяющим вершины двух противоположных углов, а эти вершины являются точками окружности. Формула
для вычисления:
a = √2 * R
где R — радиус.
Цифр после
запятой:
Результат в:
Благодаря радиусу можно найти длину диагонали, которая делит фигуру на 2 прямоугольных равнобедренных
треугольника и при помощи теоремы Пифагора найти нужную величину.
Диагональ представляет собой линию, которая соединяет две вершины противоположных углов, тем самым
разделяя правильный четырёхугольник на два равнобедренных прямоугольных треугольника. Найти значение
таким способом не сложнее, чем через площадь. Главное, знать теорему Пифагора и уметь ею
пользоваться, это самый быстрый вариант. В задачах с прямоугольными фигурами теорема часто служит
выходом из сложной ситуации.
Все вычислительные способы связаны между собой. Запомнить нужные формулы несложно. Достаточно
применять их на практике каждый день, частое использование одних и тех же алгоритмов приведет к
автоматическому запоминаю правил. Не стоит заучивать формулы, необходимо больше рассуждать
логически. Такой подход позволит решать задачи более сложного уровня и легче воспринимать любую
информацию. Самым действенным методом для запоминания является практика. Отработка нескольких
идентичных задач на определенное правило поможет закрепить результат на долгий срок.
Где d — диагональ квадрата.
Где S — площадь квадрата
Где r — радиус вписанной окружности
Где R — радиус описанной окружности
Где P — периметр квадрата.
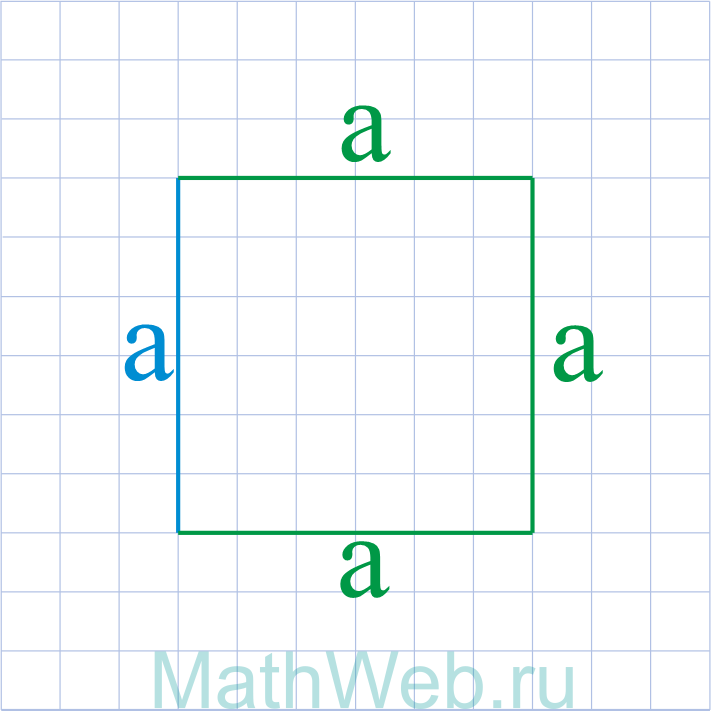
- Квадрат — это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные — перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
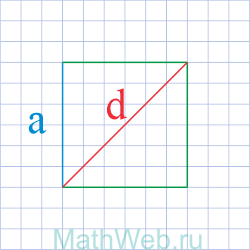 |
a = |
 |
a = √S |
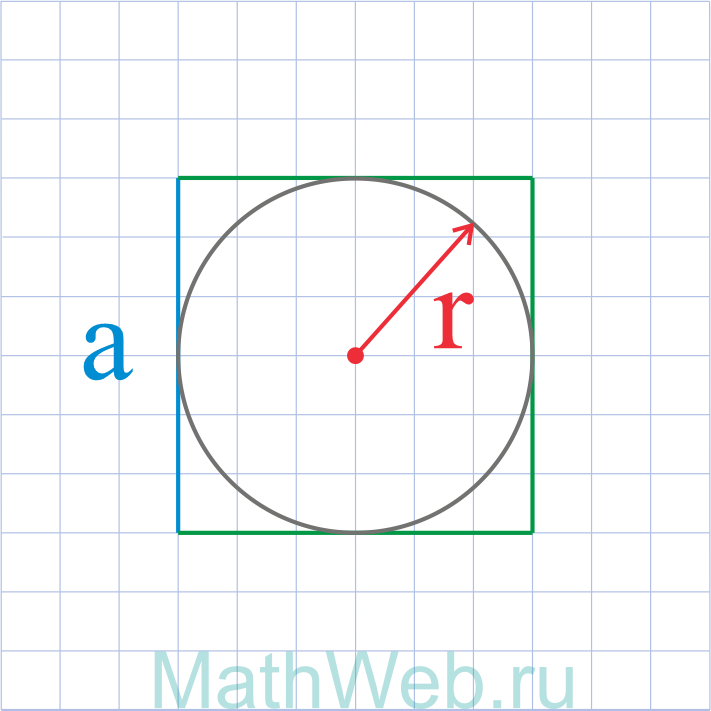 |
a = 2r |
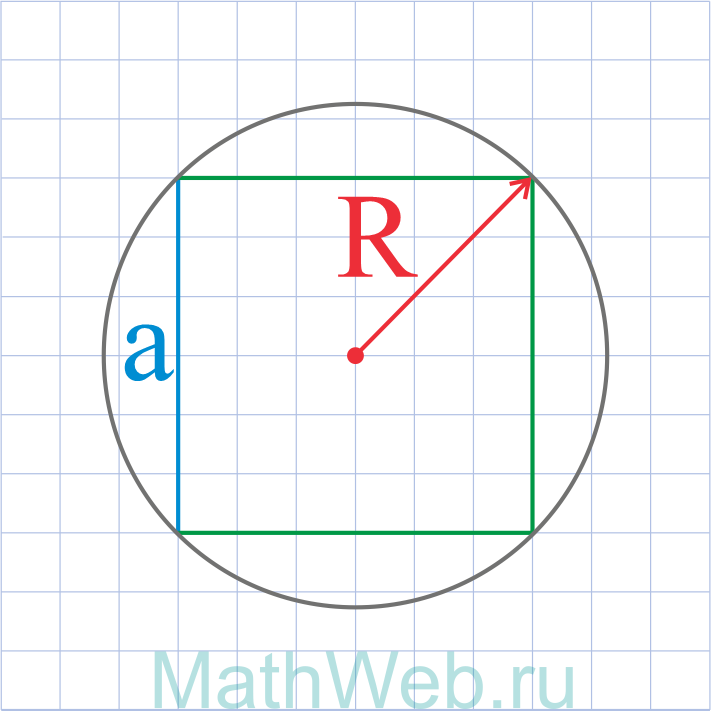 |
a = R√2 |
 |
a = |
Как найти сторону квадрата, если известна его площадь
При решении геометрических задач приходится находить одни величины, если известны другие. Так, например, если заданы три стороны треугольника, то по ним можно вычислить все его остальные характеристики. Однако, зная площадь треугольника, посчитать длину его сторон (в общем случае) невозможно. А вот если известна площадь квадрата, найти его сторону очень легко.
Вам понадобится
- калькулятор или компьютер
Инструкция
Чтобы найти сторону квадрата, если известна его площадь, извлеките из числового значения площади квадратный корень. То есть найдите такое число, квадрат (вторая степень) которого равняется площади квадрата. В виде формулы данное правило записывается следующим образом:а = √S, где:а – длина стороны квадрата,
S – площадь квадрата.Длина стороны квадрата будет измеряться в соответствующих линейных единицах. Так, например, если площадь квадрата равняется 16 квадратным сантиметрам (см²), то длина его стороны будет равняться 4 сантиметрам (см).
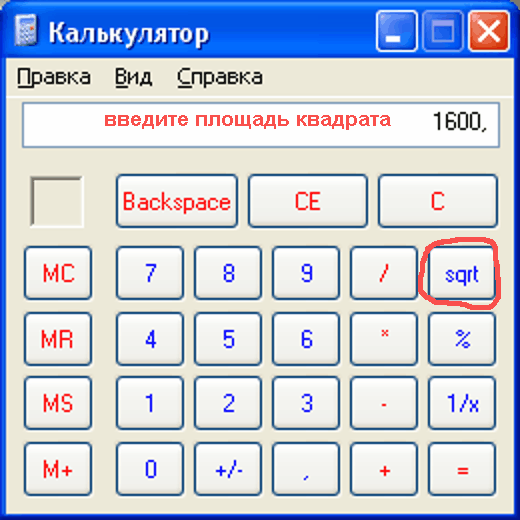
Для того чтобы посчитать корень квадратный из числа, возьмите инженерный калькулятор (такой, где имеются обозначения математических функций). Наберите на клавиатуре калькулятора числовое значение площади квадрата. Затем нажмите на кнопку, обозначенную как «√». Числовое значение длины стороны квадрата появится на индикаторе калькулятора.
Для расчета квадратного корня на компьютере запустите стандартный калькулятор Windows. Переключите его в «обычный» (не инженерный!) вид. Затем наберите значение площади. Нажмите на кнопку, обозначенную как «sqrt».
Чтобы найти сторону квадрата с заданной площадью можно воспользоваться программой MS Excel. Для этого запустите саму программу Excel, укажите курсором на произвольную клетку таблицы и нажмите кнопку «=». Затем нажмите на появившийся значок выбора функции (fx) Выберите из предложенного списка функцию «КОРЕНЬ». После чего введите в появившееся окошко числовое значение площади квадрата и нажмите кнопку «Ок» (или клавишу «Enter»). Значение корня квадратного, а соответственно и длины стороны квадрата тут же появится в данной клетке.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* — обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64