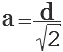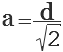/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
532 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
829 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1028 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Найти стороны квадрата через диагональ поможет теорема Пифагора.
Впрочем, если это квадрат, то нужно искать не стороны квадрата, а одну его сторону, поскольку все стороны равны.
Диагональ делит квадрат на два треугольника, для каждого треугольника (а они — прямоугольные), диагональ является гипотенузой, а стороны квадрата — катетами.
Чтобы не вводить лишние буквенные обозначения я так и обозначу: гипотенузу буквой «г», а сторону квадрата буквой «с».
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
г2 = с2 + с2 (с2 — это с в квадрате, не знаю как записать точнее )
г2 = 2 с2
с2 = г2/2 (г в квадрате, делённое на 2)
с = квадратному корню из г2/2
Г — диагональ квадрата, она известна; подставляем в формулу
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a2+a2=d2
2a2=d2
Сторона квадрата
Стороны фигур
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d2 = а2 + а2 = 2а2.
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Расчет стороны квадрата через диагональ
Расчет стороны квадрата через площадь
Доброй ночи!
Да, понять, как найти сторону квадрата если известна диагональ на первый взгляд может показаться сложным трудным. Но это вовсе не так.
Первым делом мы должны вспомнить, что диагональ квадрата – это такой отрезок, соединяющий противолежащие углы и проходит через центр. Исходя из того, что там известно, то подбирается и формула. Формула для нахождения стороны через диагональ квадрата будет таковой (изначально выводится из формулы нахождения диагонали через сторону квадрата):
где — диагональ квадрата, а
— сторона квадрата.
Используя условие задачи, мыс Вами знаем, что диагональ квадрата равняется 20 см.
Разобравшись с определёнными терминами и понятиями мы понимаем, что нам известно всё, что только нужно. И мы с лёгкостью можем подставить, уже имеющиеся значения в выведенную формулу:
Надеюсь, теперь Вам стало более понятно, как найти сторону квадрата если известна диагональ. Как Вы смогли убедиться, то в этом нет ничего сложного. Удачи Вам!
Ответ: см