Как найти сторону окружности формула - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Определение стороны окружности
Формулы стороны окружности
Ⅰ. Через диаметр и центральный угол
Ⅱ. Через площадь и центральный угол
Ⅲ. Через периметр и центральный угол
Пример решения задач по теме сторона окружности

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

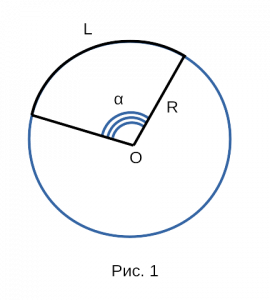
На рисунке 1, изображена окружность,
обладающая следующими величинами:

O — точка, являющаяся
центром окружности;
R — радиус
окружности;
α — центральный
угол окружности;
L — сторона
окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

[ L = frac{ pi R}{180} cdot alpha ]

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.

[ L = frac{ frac{D}{2} cdot pi}{180} cdot a ]

Ⅱ. Через площадь и центральный угол

[ L = frac{ sqrt{frac{S}{pi}} cdot pi}{180} cdot alpha ]

Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.

Ⅲ. Через периметр и центральный угол

[ L = frac{frac{P}{2pi}cdot pi}{180} cdot alpha ]

Самая краткая запись формулы
стороны окружности.

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac{frac{6}{180} cdot pi}{180} cdot 180 = frac{3 pi}{180} cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac{100}{180} cdot 60 = 0.55 cdot 60 = 33 )

Источник

Сторона окружности

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

На рисунке 1, изображена окружность,
обладающая следующими величинами:

O — точка, являющаяся
центром окружности;
R — радиус
окружности;
α — центральный
угол окружности;
L — сторона
окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Ⅱ. Через площадь и центральный угол

Ⅲ. Через периметр и центральный угол

Самая краткая запись формулы
стороны окружности.

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac<frac<6> <180>cdot pi> <180>cdot 180 = frac<3 pi> <180>cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac<100> <180>cdot 60 = 0.55 cdot 60 = 33 )

Как найти сторону окружности если известен радиус

Сторона окружности

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

На рисунке 1, изображена окружность,
обладающая следующими величинами:

O — точка, являющаяся
центром окружности;
R — радиус
окружности;
α — центральный
угол окружности;
L — сторона
окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Ⅱ. Через площадь и центральный угол

Ⅲ. Через периметр и центральный угол

Самая краткая запись формулы
стороны окружности.

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot pi> cdot 180 = frac cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot 60 = 0.55 cdot 60 = 33 )

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Треугольник. Соотношения между сторонами треугольника и радиусами вписанного и описанного кругов.

По двум сторонам a и b треугольника ABC и радиусу R описанного круга вычислить третью сторону x треугольника.

Применяя к этому четырехугольнику теорему Птоломея будем иметь:

откуда легко найдем x .

Задача будет иметь другое решение, если предположим, что стороны a и b лежат по одну сторону от центра. Применяя к этому случаю теорему Птоломея, мы получим следующее уравнение:

Теорема.

Произведение двух сторон треугольника равно:

1. произведению диаметра описанного круга на высоту, проведенную к третьей стороне.

2. квадрату биссектрисы угла, заключенного между этими сторонами, сложенному с произведением отрезков третьей стороны.

1.Обозначим стороны треугольника ABC через a, b и с, высоту, опущенную на сторону a через h_a , а радиус описанного круга через R.Проведем диаметр AD и соединим D с B.

Треугольники ABD и AEC подобны, потому что углы B и E прямые и D= С , как углы вписанные, опирающиеся на одну и ту же дугу.

Из этой формулы легко определить величину радиуса R описанного круга.

По первой теореме мы имеем: bс = 2Rh_a , где b и с есть две стороны треугольника, h_a — высота, опущенная на третью сторону треугольника, и R — радиус описанного круга.

Из этого равенства выводим:

Исключим из этой формулы высоту h_a: для этого умножим числитель и знаменатель дроби на a. Тогда, заменив произведение h_a a удвоенной площадью треугольника (которую обозначим S), получим:

Чтобы найти радиус r внутреннего вписанного круга рассмотрим треугольник АВС со вписанной в него окружностью. Отметим центр вписанной окружности и примем во внимание, что прямые OA, OB и OС разделяют данный треугольник на три других треугольника, у которых основаниями служат стороны данного треугольника, а высотой — радиус r.

Поэтому: S=1/2ar + 1/2br + 1/2cr = r ½ (a+b+c) = rp.

источники:

http://b4.cooksy.ru/articles/kak-nayti-storonu-okruzhnosti-esli-izvesten-radius

http://www.calc.ru/Treugolnik-Sootnosheniya-Mezhdu-Storonami-Treugolnika-I-Radi.html

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности.

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

M N – диаметр.

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

∪ A B = ∪ C D = α

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

l = 2 π R

Длина дуги окружности, на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.

Например, на рисунке 8.107 $LaTeX formula: angle A+angle C=angle B+angle D=180^{circ}$ .

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=frac{a}{sqrt{3}}$ , (8.34)

$LaTeX formula: r=frac{a}{2sqrt{3}}$ ; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: R=frac{abc}{4S}$ , (8.36)

$LaTeX formula: r=frac{2S}{a+b+c}$ ; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=frac{c}{2}$ , (8.38)

$LaTeX formula: r=frac{a+b-c}{2}$ ; (8.39)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=frac{d}{2}$ , (8.40)

$LaTeX formula: r=frac{a}{2}$ ; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=frac{d}{2}$ ; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=frac{h}{2}$ ; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=frac{h}{2}$ . (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле $LaTeX formula: R=frac{abc}{4S}$ найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

для правильного шестиугольника со стороной :

, (8.45)

$LaTeX formula: r=frac{asqrt{3}}{2}$ . (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32, а площадь квадрата со стороной находят по формуле $LaTeX formula: S=a^{2}$ , то согласно условию задачи запишем: $LaTeX formula: S_{square }-S_{bigcirc }=12$ , $LaTeX formula: pi r^{2}-a^{2}=2pi -8$ .

А так как $LaTeX formula: r=frac{a}{2}$ , то $LaTeX formula: frac{pi a^{2}}{4}-a^{2}=2pi -8$ , $LaTeX formula: pi a^{2}-4a^{2}=4(2pi -8)$ , $LaTeX formula: a^{2}(pi -4)=8(pi -4)$ , $LaTeX formula: a^{2}=8$ , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , $LaTeX formula: x^{2}+3x-4=0$ , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: $LaTeX formula: d^{2}=1+16=17$ , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

$LaTeX formula: a^{2}=left (frac{d_{1}}{2} right )^{2}+left ( frac{d_{2}}{2} right )^{2}$ , $LaTeX formula: a^{2}=3^{2}+4^{2}$ , .

По формуле 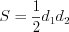$LaTeX formula: S=frac{1}{2}d_{1}d_{2}$ найдем площадь ромба: $LaTeX formula: S=frac{1}{2}cdot 6cdot 8=24$ .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной находят по формуле: $LaTeX formula: S=frac{sqrt{3}a^{2}}{4}$ .

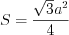
Зная площадь треугольника, найдем его сторону: $LaTeX formula: frac{sqrt{3}a^{2}}{4}=4sqrt{3}$ , $LaTeX formula: a^{2}=16$ , .

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: $LaTeX formula: r=frac{4}{2sqrt{3}}=frac{2}{sqrt{3}}$ .

По формуле 8.30 найдем длину окружности: $LaTeX formula: C=frac{4pi }{sqrt{3}}$ .

Ответ: $LaTeX formula: frac{4sqrt{3}pi }{3}$ .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38. Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора $LaTeX formula: c^{2}=2a^{2}$ , откуда $LaTeX formula: a=frac{C}{sqrt{2}}$ , $LaTeX formula: a=frac{4}{sqrt{2}}=2sqrt{2}$ .

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае $LaTeX formula: r=frac{2a-c}{2}$ , $LaTeX formula: r=frac{4sqrt{2}-4}{2}=2sqrt{2}-2$ .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора $LaTeX formula: BC^{2}=AC^{2}+AB^{2}$ или $LaTeX formula: 25+10x+x^{2}=64+9+6x+x^{2}$ , откуда , .

Найдем катет : .

Найдем площадь треугольника: $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot ACcdot AB$ , $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot 8cdot 15=60$ .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: $LaTeX formula: frac{6}{4}=frac{x}{8}$ , откуда .

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона найдем площадь треугольника. Так как , то .

Тогда $LaTeX formula: r=frac{18sqrt{15}}{30}=frac{3sqrt{15}}{5}=0,6sqrt{15}$ .

Ответ: .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 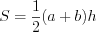$LaTeX formula: S=frac{1}{2}(a+b)h$ найдем площадь трапеции: $LaTeX formula: S=frac{1}{2}cdot 15cdot 6=45$ .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .

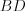
Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

$LaTeX formula: R=frac{ABcdot BDcdot AD}{4cdot S_{triangle ABD}}=frac{ABcdot BDcdot AD}{4cdot frac{1}{2}cdot ADcdot BN}$ , $LaTeX formula: R=frac{ABcdot BD}{2cdot BN}$ .

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то $LaTeX formula: frac{1}{2}(5k +12k)=17$ , откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда $LaTeX formula: AN=KD=frac{1}{2}(24-10)=7$ .

Согласно теореме Пифагора запишем:

$LaTeX formula: AB=sqrt{AN^{2}+BN^{2}}$ , $LaTeX formula: AB=sqrt{17^{2}+7^{2}}=sqrt{338}$ ;

$LaTeX formula: BD=sqrt{BN^{2}+ND^{2}}$ , $LaTeX formula: BD=sqrt{17^{2}+17^{2}}=17sqrt{2}$ .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=frac{sqrt{338}cdot 17sqrt{2}}{2cdot 17}=frac{2cdot 13}{2}=13$ .

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: .

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то $LaTeX formula: r=frac{3}{2}$ .

Площадь круга находят по формуле 8.32. Тогда $LaTeX formula: S_{1}=3pi$ , а $LaTeX formula: S_{2}=frac{9pi}{4}$ .

Найдем площадь кольца: $LaTeX formula: S_{K}=S_{1}-S_{2}$ , $LaTeX formula: S_{K}=3pi -frac{9pi }{4}=frac{3pi }{4}$ .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=pi R^{2}$ . (8.32)

Источник

Содержание

Основные определения и свойства
Чем круг отличается от окружности: объяснение
Круг и окружность: примеры, фото
Свойства окружности
Свойство 1
Свойство 2
Свойство 3
Формулы
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Формула длины окружности и площади круга: сравнение
Площадь круга
Длина окружности
Как найти длину окружности через диаметр
Как найти длину окружности через радиус
Как вычислить длину окружности через площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Длина дуги
Площадь сектора
Площадь сегмента
Уравнение окружности
Касательная окружности и ее свойства
Основные свойства касательных к окружности
Секущая окружности и ее свойства
Основные свойства секущих
Хорда окружности ее длина и свойства
Длина хорды
Основные свойства хорд
Центральный угол, вписанный угол и их свойства
Основные свойства углов
Вписанная окружность
Описанная окружность
Теорема Птолемея
Задачи для решения

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга		Часть окружности, расположенная между двумя точками окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Сектор		Часть круга, ограниченная двумя радиусами
Сегмент		Часть круга, ограниченная хордой
Правильный многоугольник		Выпуклый многоугольник, у которого все стороны равны и все углы равны
	Около любого правильного многоугольника можно описать окружность

Окружность

Длина окружности дуги площадь круга сектора сегмента число пи

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Чем круг отличается от окружности: объяснение

Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:

Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
Сходство между окружностью и кругом: радиус и диаметр;
У круга и окружности единый центр;
В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Круг и окружность: примеры, фото

Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.

Сравнение между кругом и окружностью

Свойства окружности

Свойство 1

Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.

Свойство 2

Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3

Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.

Формулы

Диаметр окружности (d):

Длина окружности (С):

Радиус окружности (R):

Формулы для площади круга и его частей

Числовая характеристика	Рисунок	Формула
Площадь круга		, где R – радиус круга, D – диаметр круга
Площадь сектора		, если величина угла α выражена в радианах
, если величина угла α выражена в градусах
Площадь сегмента		, если величина угла α выражена в радианах
, если величина угла α выражена в градусах

Площадь круга

где R – радиус круга, D – диаметр круга

Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

Числовая характеристика	Рисунок	Формула
Длина окружности		C = 2πR = π D, где R – радиус круга, D – диаметр круга
Длина дуги		L(α) = αR, если величина угла α выражена в радианах
, если величина угла α выражена в градусах

Длина окружности

C = 2πR = π D,

где R – радиус круга, D – диаметр круга

Длина дуги

L(α) = αR,

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Формула длины окружности и площади круга: сравнение

Формула длины окружности L=2 πR

Формула площади круга S= πR²

Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.

Площадь круга

Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан – угольникnправильный (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1

равнаR, – угольника, вписанного в окружность радиуса nПлощадь правильного

, равна1 – угольника, вписанного в окружность радиуса nПлощадь правильного

Следовательно,

Поскольку π, стремится к 1 – угольника, вписанного в окружность радиуса n площадь правильного nпри увеличении , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.

Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR2.

Длина окружности

Рассмотрим – угольникnправильный B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

Поскольку – угольникаnплощадь B1B2…Bn равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

Следствие. Длина окружности радиуса 1 равна 2π.

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, равное 3,14

r — радиус окружности

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

π — число пи, равное 3,14
S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

l=πd, где

π — число пи, равное 3,14
d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

l=πa, где

π — математическая константа, равная 3,14
a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:

где:

π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

Рис.4

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5

Уравнение окружности

Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r2 = x2 + y2

Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r2 = (x — a)2 + (y — b)2

Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
y = b + r sin t

Касательная окружности и ее свойства

Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ2

Хорда окружности ее длина и свойства

Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

Длина хорды через центральный угол и радиус:

AB = 2r sin α2

Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

Чем больше хорда тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Центральный угол окружности — угол, вершиной которого есть центр окружности.

Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

β = α2

Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.Определение.Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла,который ограничивает эту дугу своими сторонами.
Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение.Полуокружность — дуга в которой концы соединены диаметром окружности.Определение.Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.Определение.Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула.Формула площади сектор через центральный угол (в градусах)

S = πr2360°∙ α

Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Вписанная окружность

Окружность называетсявписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

S=pr
,

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен r=S/p

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен r=S/p
. Здесь

Описанная окружность

Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна $180^{circ}$
.

∠
+∠
=∠
+∠ $D=180^{circ}$

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

Где — длины сторон треугольника, — его площадь.

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

l=πd

Подставляем туда известные переменные и получается, что длина окружности равна

l=πd=3,14·5=15,7(см)

Ответ: 15,7 (см)

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен
Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Так и сделаем:

l=2πr=2·π·4≈2·3,14·4=25,12(дм)

Ответ: l=25,12(дм)

Источник