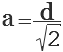Найти стороны квадрата через диагональ поможет теорема Пифагора.
Впрочем, если это квадрат, то нужно искать не стороны квадрата, а одну его сторону, поскольку все стороны равны.
Диагональ делит квадрат на два треугольника, для каждого треугольника (а они — прямоугольные), диагональ является гипотенузой, а стороны квадрата — катетами.
Чтобы не вводить лишние буквенные обозначения я так и обозначу: гипотенузу буквой «г», а сторону квадрата буквой «с».
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
г2 = с2 + с2 (с2 — это с в квадрате, не знаю как записать точнее )
г2 = 2 с2
с2 = г2/2 (г в квадрате, делённое на 2)
с = квадратному корню из г2/2
Г — диагональ квадрата, она известна; подставляем в формулу
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* — обязательно заполнить
Диагональ, диаметр описанной окружности (M) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{frac{M^{2}}{2}}) = (sqrt{frac{10^{2}}{2}}) = 7.07
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{7.07}{2}) = 3.54
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{10}{2}) = 5
Периметр (P) = (L*4) = (7.07*4) = 28.28
Площадь (S) = (L^{2}) = (7.07^{2}) = 49.98
Сторона квадрата
Стороны фигур
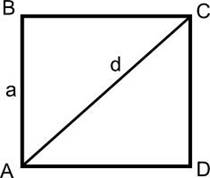
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d2 = а2 + а2 = 2а2.
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Расчет стороны квадрата через диагональ
Расчет стороны квадрата через площадь
Как найти сторону квадрата, зная его диагональ
Квадратом называют ромб с прямыми углами. Эта фигура одновременно является параллелограммом, прямоугольником и ромбом, обладая исключительными геометрическими свойствами. Найти сторону квадрата через его диагональ можно несколькими способами.
Поскольку удиагонали равны между собой (это свойство ему досталось «по наследству» от прямоугольника), то для того, чтобы найти сторону квадрата достаточно знать длину одной диагонали. Диагональ и две стороны квадрата, примыкающие к ней, представляют прямоугольный (поскольку все углы квадрата прямые) и равнобедренный (так как все стороны этой фигуры равны) треугольник. В этом треугольнике стороны квадрата являются катетами, а диагональ гипотенузой. Чтобы найти сторону квадрата, воспользуйтесь теоремой Пифагора.
Поскольку сумма квадратов катетов, которые равны a, равна квадрату гипотенузы, которую обозначьтеc (c²=a²+a²), то катет будет равен гипотенузе, поделенной на корень квадратный из числа 2, что проистекает и предыдущего выражения a=c/√2. Например, чтобы найти сторону квадрата с диагональю 12 см, это число поделите на корень квадратный из 2. Получите a=12/√2≈8,5 см. С учетом того, что корень квадратный из 2 нацело не извлекается, все ответы придется округлять с нужной точностью.
Сторону квадрата найдите, используя соотношение углов и сторон в прямоугольном треугольнике, который образуется диагональю и примыкающими к ней сторонами. Известно, что один из углов этого треугольника прямой (как угол между сторонами квадрата), а два других равны между собой и составляют 45º. Это свойство проистекает из равнобедренности этого треугольника, поскольку катеты его равны между собой.
Чтобы найти сторону квадрата, умножьте диагональ на синус или косинус угла 45º (они равны между собой, как прилежащий и противолежащий катеты sin(45º)=cos(45º)=√2/2) a=c∙√2/2. Например, дана диагональ квадрата, равная 20 см, нужно найти его сторону. Произведите расчет согласно указанной выше формуле, результатом будет сторона квадрата с нужной степенью точностиa=20∙√2/2≈14,142 см.
Как найти сторону квадрата если известна диагональ?
В прошлый раз мы вывели формулу, как найти диагональ в квадрате.
Теперь нам нужно лишь вывести нашу формулу в обратную сторону.
Я не буду здесь заново выводить формулу, по которой можно найти диагональ квадрата. Вот она:
d = √2a²
Где d — диагональ квадрата,
√ — корень,
a² — сторона в квадрате.
Теперь из формулы подсчета размера диагонали d = √2a² , нам нужно вывести значение «а» — стороны квадрата.
Возведем эту формулу в квадрат, у нас получится:
d² = 2a²
Далее разделим нашу формулу на 2, у нас получится вот так:
d²/2 = a²
Для удобства чтения поменяем местами значения.
a² = d²/2
Ну и далее извлечём из всего корень! И получим: что сторона квадрата равна корню из квадрата диагонали деленного на 2.
a = √d²/2
Написать что-нибудь…
найти сторону квадрата по диагонали
сторона квадрата через диагональ
сторона квадрата по диагонали
найти сторону квадрата по диагонали