Как найти сторону основания квадратной пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти сторону основания пирамиды

Задачи на вычисление стороны основания пирамиды составляют в задачнике по геометрии довольно большой раздел. Очень многое зависит от того, какая гемоетрическая фигура лежит в основании, а также от того, что дано в условиях задачи.

Вам понадобится

— чертежные принадлежности;
— тетрадь в клетку;
— теорема синусов;
— теорема Пифагора;
— калькулятор.

Инструкция

В школьном курсе геометрии рассматриваются главным образом пирамиды, в основании которых лежит правильный многоугольник, то есть такой, у которого все стороны равны. Проекция вершины пирамиды совпадает с центром ее основания. Начертите пирамиду, в основании которой лежит равносторонний треугольник. В условиях могут быть даны:
— длина бокового ребра пирамиды и угол его с ребром между боковой гранью и основанием;
— длина бокового ребра и высота боковой грани;
— длина бокового ребра и высота пирамиды.

Если известны боковое ребро и угол, задача решается несколько иначе. Вспомните, что собой представляет каждая боковая грань пирамиды, в основании которой лежит равносторонний многоугольник. Это равнобедренный треугольник. Проведите его высоту, которая одновременно является биссектрисой и медианой. То есть половина стороны основания a/2=L*cosA, где а – сторона основания пирамиды, L – длина ребра. Чтобы найти размер стороны основания, достаточно полученный результат умножить на 2.

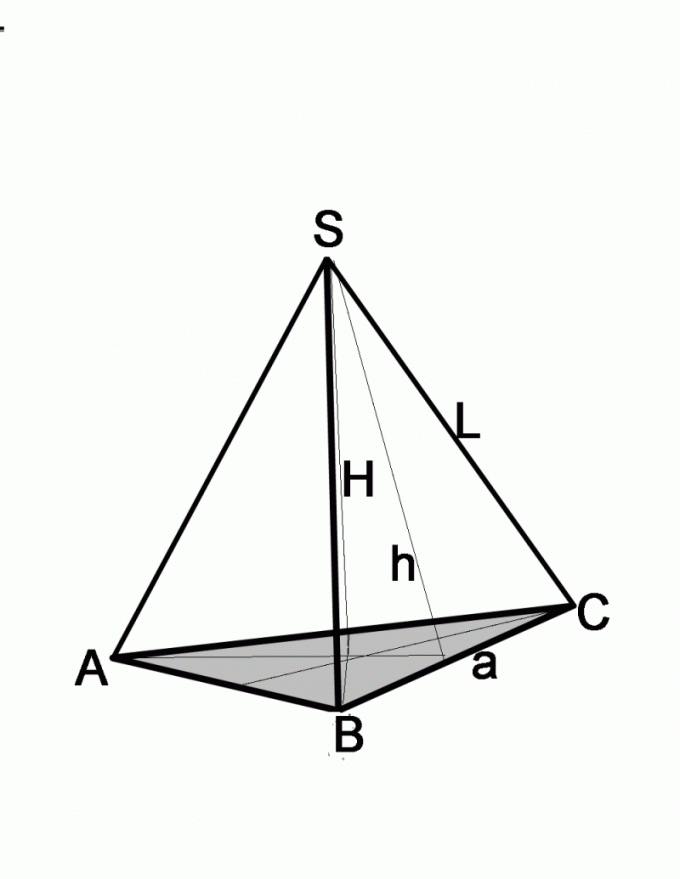
Если в задаче даны высота боковой грани и длина ребра, найдите сторону основания по теореме Пифагора. Боковая грань в данном случае будет гипотенузой, известная высота –з одним из катетов. Чтобы найти длину второго катета, нужно из квадрата гипотенузы вычесть квадрат второго катета, то есть (a/2)2=L2-h2, где а – сторона основания, L – длина боковой грани, h – высота боковой грани.

В этом случае нужно выполнить дополнительное построение, чтобы можно было оперировать тригонометрическими функциями. Вам даны боковое ребро L и высота пирамиды H, которая соединяет вершину пирамиды с центром основания. Из точки пересечения высоты с плоскостью основания проведите отрезок, соединив эту точку с одним из углов основания. У вас получился прямоугольный треугольник, гипотенузой которого является боковое ребро, одним из катетов – высота пирамиды. По этим данным легко найти второй катет треугольника, для этого достаточно из квадрата бокового ребра L вычесть квадрат высоты H. Дальнейшие действия зависят от того, какая именно фигура лежит в основании.

Вспомните свойства равностороннего треугольника. У него высоты одновременно являются биссектрисами и медианами. В точке пересечения они делятся пополам. То есть получается, что вы нашли половину высоты основания. Для удобства вычислений проведите все три высоты. Вы увидите, что отрезок, квадрат длины которого вы уже нашли, является гипотенузой прямоугольного треугольника. Извлеките квадратный корень. Вам известен и острый угол – 30°, так что найти половину стороны основания не составит особого труда, применив теорему косинусов.

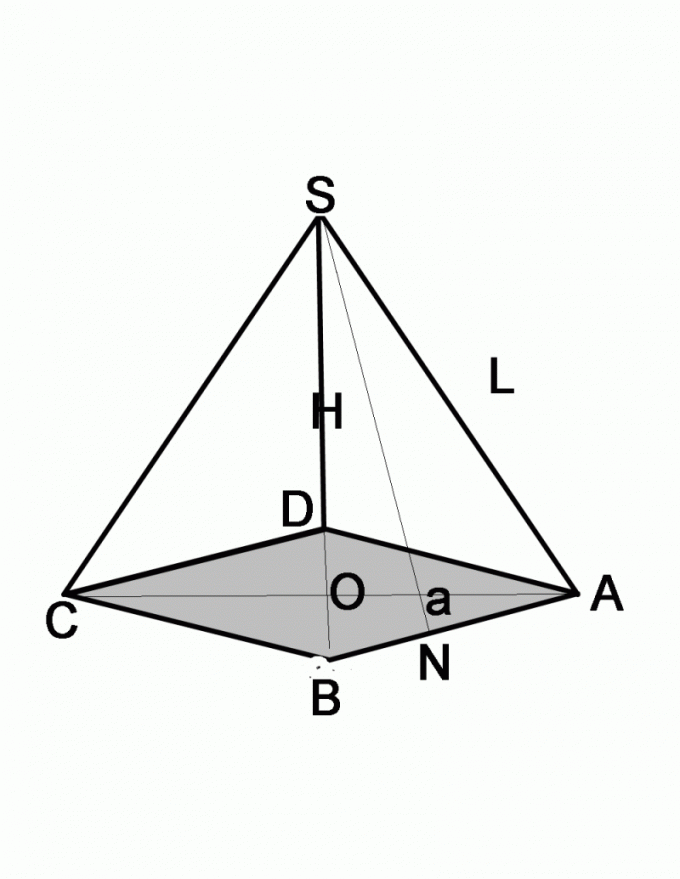
Для пирамиды, в основании которой лежит правильный четырехугольник, алгоритм будет тем же самым. Если вы вычтите из квадрата бокового ребра квадрат высоты пирамиды, получите возведенную в квадрат половину диагонали основания. Извлеките корень, найдите размер диагонали, которая одновременно является гипотенузой равнобедренного прямоугольного треугольника. Размер любого из катетов найдите по теореме Пифагора, синусов или косинусов.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan⁡〖(180°)/n〗 )

Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan⁡〖(180°)/n〗 )

Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin⁡〖(180°)/n〗 )

Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n

Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin⁡〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)

Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cos⁡α=R/b=a/(2b sin⁡〖(180°)/n〗 )
cos⁡β=r/l=a/(2 tan⁡〖(180°)/n〗 √(b^2-a^2/4))

Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan⁡〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan⁡〖(180°)/n〗 ))

Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin⁡〖(180°)/n〗 ))^2 ))/(12 tan⁡〖(180°)/n〗 )

Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin⁡〖(180°)/n〗 ))^2 ))/(tan⁡〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan⁡〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin⁡〖(180°)/n〗 ))^2 ))

Источник

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

похожие вопросы 5

Источник

Загрузить PDF

Квадратная пирамида – объемная фигура с основанием в виде квадрата и треугольными боковыми гранями. Вершина квадратной пирамиды проецируется в центр основания. Если «а» — сторона квадратного основания, «h» — высота пирамиды (перпендикуляр, опущенный из вершины пирамиды к центру ее основания), тогда объем квадратной пирамиды можно вычислить по формуле: a² × (1/3)h. Эта формула верна для квадратной пирамиды любых размеров (от сувенирных пирамид до египетских пирамид).

1
Найдите сторону основания. Так как в основании квадратной пирамиды лежит квадрат, то все стороны основания равны. Поэтому необходимо найти длину любой стороны основания.
- Например, дана пирамида, сторона основания которой равна 5 см.
- Если стороны основания не равны друг другу, то вам дана прямоугольная, а не квадратная пирамида. Тем не менее, формула для вычисления объема прямоугольной пирамиды похожа на формулу для вычисления объема квадратной пирамиды. Если «l» и «w» — две смежные (неравные) стороны прямоугольника в основании пирамиды, то объем пирамиды вычисляется по формуле: (l× w) × (1/3)h
2
Вычислите площадь квадратного основания, умножив его сторону саму на себя (или, другими словами, возведя сторону в квадрат).
- В нашем примере: 5 х 5 = 5² = 25 см².
- Не забудьте, что площадь измеряется в квадратных единицах — квадратных сантиметрах, квадратных метрах, квадратных километрах и так далее.
3
Умножьте площадь основания на высоту пирамиды. Высота — перпендикуляр, опущенный из вершины пирамиды на ее основание. Перемножив эти величины, вы получите объем куба с тем же основанием и высотой, как у пирамиды.
- В нашем примере высота равна 9 см: 25 см² × 9 см = 225 см³
- Не забывайте, что объем измеряется в кубических единицах, в данном случае в кубических сантиметрах.
4
Разделите полученный результат на 3 и вы найдете объем квадратной пирамиды.
- В нашем примере: 225 см³ / 3 = 75 см³.
- Объем измеряется в кубических единицах.
Реклама

1
Если вам дана либо площадь, либо высота пирамиды и ее апофема, вы можете найти объем пирамиды, используя теорему Пифагора. Апофема – это высота наклонной треугольной грани пирамиды, проведенная из вершины треугольника к его основанию. Для вычисления апофемы используйте сторону основания пирамиды и ее высоту.
- Апофема делит сторону основания пополам и пересекает ее под прямым углом.
2
Рассмотрите прямоугольный треугольник, образованный апофемой, высотой и отрезком, соединяющим центр основания и середину его стороны. В таком треугольнике апофема является гипотенузой, которую можно найти по теореме Пифагора. Отрезок, соединяющий центр основания и середину его стороны, равен половине стороны основания (этот отрезок является одним из катетов; вторым катетом является высота пирамиды).
- Напомним, что теорема Пифагора записывается так: a² + b² = c², где «a» и «b» — катеты, «c» — гипотенуза прямоугольного треугольника.
- Например, дана пирамида, у которой сторона основания равна 4 см, а апофема — 6 см. Чтобы найти высоту пирамиды, подставьте эти значения в теорему Пифагора.
  - a² + b² = c²
  - a² + (4/2)² = 6²
  - a² = 32
  - a = √32 = 5,66 см Вы нашли второй катет прямоугольного треугольника, который является высотой пирамиды (аналогично, если была бы дана апофема и высота пирамиды, вы бы могли найти половину стороны основания пирамиды).
3
Используйте найденное значение, чтобы найти объем пирамиды по формуле: a² × (1/3)h.
- В нашем примере вы вычислили, что высота пирамиды равна 5,66 см. Подставьте необходимые значения в формулу для вычисления объема пирамиды:
  - a² × (1/3)h
  - 4² × (1/3)(5,66)
  - 16 × 1,89 = 30,24 см³.
4
Если вам не дана апофема, используйте ребро пирамиды. Ребро – это отрезок, соединяющий вершину пирамиды с вершиной квадрата в основании пирамиды. В этом случае вы получите прямоугольный треугольник, катетами которого являются высота пирамиды и половина диагонали квадрата в основании пирамиды, а гипотенузой – ребро пирамиды. Так как диагональ квадрата равна √2 × сторону квадрата, то вы можете найти сторону квадрата (основания), разделив диагональ на √2. Затем вы сможете найти объем пирамиды по вышеописанной формуле.
- Например, дана квадратная пирамида с высотой 5 см и ребром 11 см. Вычислите половину диагонали следующим образом:
  - 5² + b² = 11²
  - b² = 96
  - b = 9,80 см.
  - Вы нашли половину диагонали, поэтому диагональ равна: 9,80 см × 2 = 19,60 см.
  - Сторона квадрата (основания) равна √2 × диагональ, поэтому 19,60 / √2 = 13,90 см. Теперь найдите объем пирамиды по формуле:a² × (1/3)h
  - 13,90² × (1/3)(5)
  - 193,23 × 5/3 = 322,05 см³
Реклама

Советы

В квадратной пирамиде ее высота, апофема и сторона основания связаны теоремой Пифагора: (сторона ÷ 2)² + (высота)² = (апофема)²
В любой правильной пирамиде апофема, сторона основания и ребро связаны теоремой Пифагора: (сторона ÷ 2)² + (апофема)² = (ребро)²

Об этой статье

Эту страницу просматривали 11 790 раз.

Была ли эта статья полезной?

Источник

In geometry, a pyramid is a three-dimensional shape with a polygonal base and three or more triangular faces that meet at a common point above the base, known as the apex or vertex. A pyramid is a polyhedron that is classified according to the shape of its polygonal base, such as

Triangular pyramid
Rectangular pyramid
Square pyramid
Pentagonal pyramid
Hexagonal pyramid

The apex is the meeting point of a pyramid’s lateral surfaces or side faces. The perpendicular distance from the center of the base to the apex is called the height of a pyramid, while the slant height of a pyramid is defined as the perpendicular distance between the apex and the base of a lateral surface.

Square Pyramid

A square pyramid is also known as a pentahedron as it has five faces, including a square base and four triangular faces that meet at a point at the top called the apex. The Great Pyramid of Giza is the best example of a square pyramid. A square pyramid is a pyramid that has a square base and four triangular faces (lateral faces). It has five (5) faces four (4) triangular faces, a square base, five (5) vertices, and eight (8) edges.
Square pyramids can be distinguished depending upon the lengths of their edges, the position of the apex, and so on. The different types of square pyramids are equilateral square pyramids, right square pyramids, and oblique square pyramids.

Equilateral square pyramid: An equilateral square pyramid is a square pyramid where all the triangular faces of a square pyramid have equal edges.
Right square pyramid: A right square pyramid is a square pyramid with the apex just above the center of the base, such that a straight line from the apex cuts the base perpendicularly.
Oblique square pyramid: An oblique square pyramid is a square pyramid where the apex is not aligned right above the center of the base.

Regular Square Pyramid Formulae

There are two types of surface areas, namely, the lateral surface area and the total surface area. A pyramid’s total surface area is calculated by adding the areas of its base, side faces, and lateral surfaces, while the lateral surface area of a pyramid is calculated by adding the sum of its lateral surfaces, or side faces.

Lateral surface area of the regular square pyramid (LSA)= 2al square units

Total surface area of a regular square pyramid (TSA) = 2al + a² square units

Where “a” is the base edge, and “l” is the slant height.

The slant height of the pyramid (l) = √[(a/2)² + h²]

Now,

Lateral surface area of the square pyramid (LSA)= 2a√(a²/4 + h²) square units

Total surface area of a regular square pyramid (TSA) = a² + 2a√(a²/4 + h²) square units

Volume of Regular Square Pyramid

The formula to determine the volume of a pyramid is given as,

The volume of a pyramid = 1/3×Ah cubic units

Where h is the height of the pyramid and A is the area of the base

Here, as the base of the pyramid is a square,

Base area = a²

Now,

Volume of the regular square pyramid (V)= (1/3)a²h cubic units

Where “a” is the base edge, and “h” is the height of the pyramid.

Practise Problems based on Regular Square Pyramid Formula

Problem 1: Calculate a square pyramid’s total surface area if the base’s side length is 20 inches and the pyramid’s slant height is 25 inches.

Solution:

Given,

The side of the square base (a) = 20 inches, and

Slant height, l = 25 inches

The perimeter of the square base (P) = 4a = 4(20) = 80 inches

The lateral surface area of a regular square pyramid = (½) Pl

LSA = (½ ) × (80) × 25 = 1000‬ sq. in

Now, the total surface area = Area of the base + LSA

= a² + LSA

= (20)² + 1000‬

= 400 + 1000 = 1400 sq. in

Hence, the total surface area of the given pyramid is 1400 sq. in.

Problem 2: Calculate the slant height of the regular square pyramid if its lateral surface area is 192 sq. cm and the side length of the base is 8 cm.

Solution:

Given data,

Length of the side of the base (a) = 8 cm

The lateral surface area of a regular square pyramid = 192 sq. cm

Slant height (l) = ?

We know that,

The lateral surface area of a regular square pyramid = (½) Pl

The perimeter of the square base (P) = 4a = 4(8) = 32 cm

⇒ 192 = ½ × 32 × l

⇒ l = 12 cm

Hence, the slant height of the square pyramid is 12 cm.

Problem 3: What is the volume of a regular square pyramid if the sides of a base are 10 cm each and the height of the pyramid is 15 cm?

Solution:

Given data,

Length of the side of the base (a)= 10 cm

Height of the pyramid (h) = 15 cm.

The volume of a regular square pyramid (V) = 1/3 × Area of square base × Height

Area of square base = a² = (10)² = 100 sq. cm

V = 1/3 × (100) ×15 = 500 cu. cm

Hence, the volume of the given square pyramid is 500 cu. cm.

Problem 4: Calculate the lateral surface area of a regular square pyramid if the side length of the base is 7 cm and the pyramid’s slant height is 12 cm.

Solution:

Given,

The side of the square base (a) = 7 cm

Slant height, l = 12 cm

The perimeter of the square base (P) = 4a = 4(7) = 28 cm

The lateral surface area of a regular square pyramid = (½) Pl

LSA = (½ ) × (28) × 12 = 168‬ sq. cm

Hence, the lateral surface area of the given pyramid is 168 sq. cm.

Problem 5: Calculate the height of the regular square pyramid if its volume is 720 cu. in. and the side length of the base is 12 inches.

Solution:

Given,

The side of the square base (a) = 12 cm

Volume = 720 cu. in

Height (H) =?

We know that,

The volume of a regular square pyramid (V) = 1/3 × Area of square base × Height

Area of square base = a² = (12)² = 144 sq. in

⇒ 720 = 1/3 × 144 × H

⇒ 48H = 720

⇒ H = 720/48 = 15 inches

Hence, the height of the square pyramid is 15 inches.

Problem 6: Calculate the volume of a regular square pyramid if the base’s side length is 8 inches and the pyramid’s height is 14 inches.

Solution:

Given data,

Length of the side of the base of a square pyramid = 8 inches

Height of the pyramid = 14 inches.

The volume of a regular square pyramid (V) = (1/3)a²h cubic units

V = (1/3) × (8)² ×14

= (1/3) × 64 × 14

= 298.67 cu. in

Hence, the volume of the given square pyramid is 298.67 cu. in.

Problem 7: Find the surface area of a regular square pyramid if the base’s side length is 15 units and the pyramid’s slant height is 22 units.

Solution:

Given,

The side of the square base (a) = 15 units, and

Slant height, l = 22 units.

We know that,

The total surface area of a regular square pyramid (TSA) = 2al + a² square units

= 2 × 15 × 22 + (15)²

= 660 + 225= 885 sq. units

Hence, the total surface area of the given pyramid is 885 sq. units.

Frequently Asked Questions on Square Pyramid

Question 1: What is a square pyramid?

Answer:

Square pyramid is a 3-D figure with a square base and four triangular faces joined at a vertex.

Question 2: Mention the few properties of a square pyramid?

Answer:

Few properties of square pyramid are:

Square Pyramid has the base of a square.

It has five vertices and four triangular faces.

Square Pyramid has 8 edges.

Question 3: What is the formula for the volume of a square pyramid?

Answer:

Formula for the volume of a square pyramid is

Volume = (⅓)×(Base area of a square)×(Height of the square pyramid) cubic units.

Источник