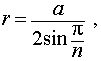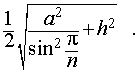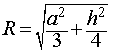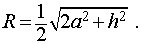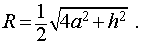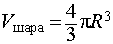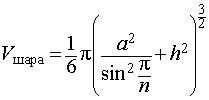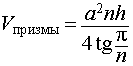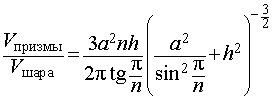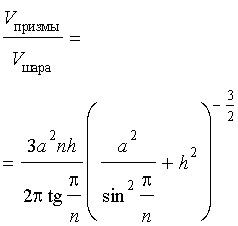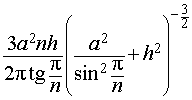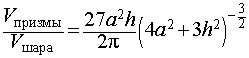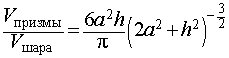Как найти сторону призмы через окружность - Исправление недочетов и поиск решений вместе с Examum.ru

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

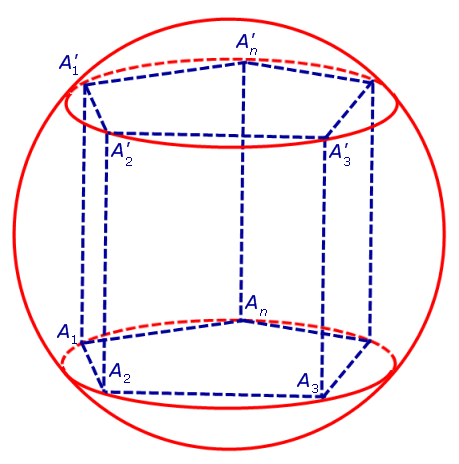
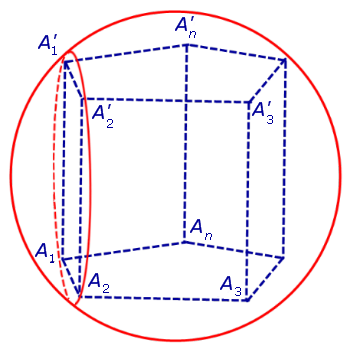
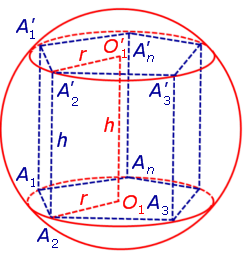
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

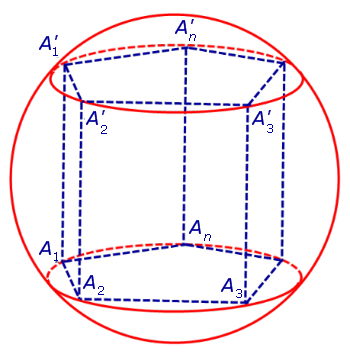
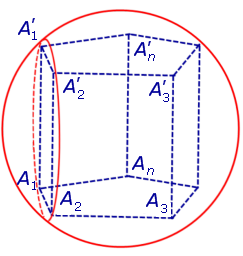
Каждая из боковых граней призмы также вписана в окружность (рис. 2).

Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

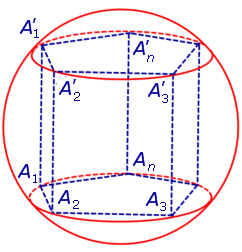
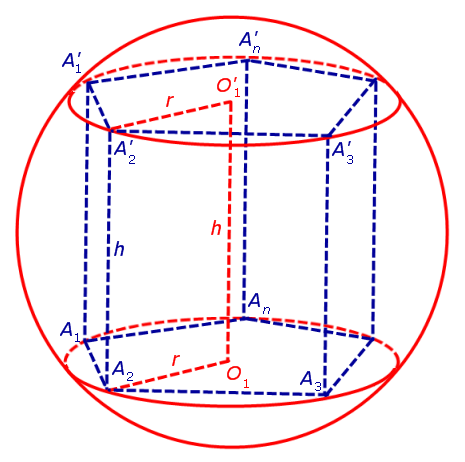
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

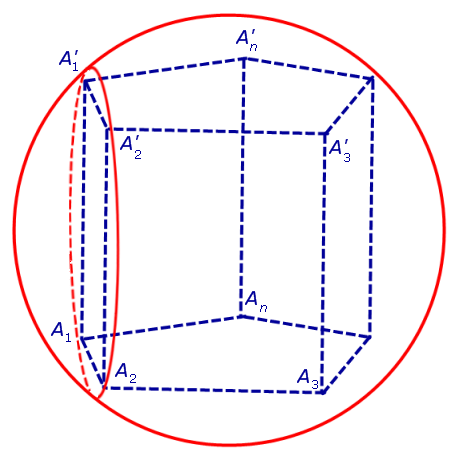
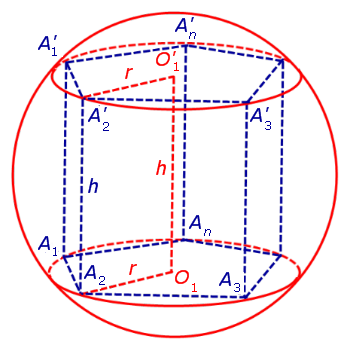
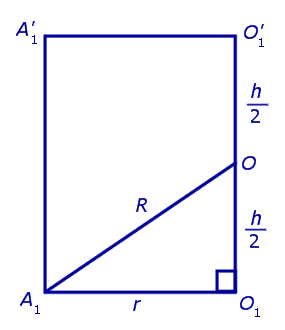
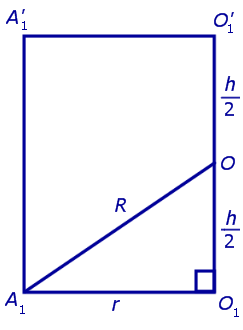
Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

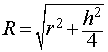(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Радиус сферы, описанной около правильной n — угольной призмы

то из формулы (1) получаем выражение для радиуса описанной сферы

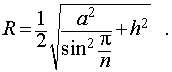(2)

Ответ.

Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

Ответ.

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

источники:

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

http://www.resolventa.ru/uslugi/priceegerus1.htm

Источник

Зная боковое ребро и высоту основания треугольной призмы можно рассчитать ее сторону основания, площадь основания, а также радиусы вписанной и описанной окружностей и периметр треугольной призмы.

Сторона основания через высоту основания треугольной призмы будет равна высоте, умноженной на корень из двух. Чтобы найти площадь основания, нужно это выражение возвести в квадрат и умножить на корень из трех, деленный на четыре. Радиусы вписанной и описанной окружности в основание, вычисляются по формулам для равностороннего треугольника, в которые нужно подставить выражение через высоту, а для того чтобы найти периметр призмы, необходимо сложить вместе три боковых ребра и шесть сторон основания.
a=h√2
S_(осн.)=(√3 h^2)/2
r= h/√6
R=(a√2)/√3
P=3(2a+b)

Зная площадь основания треугольной призмы через высоту, можно вычислить также площадь боковой поверхности, и, сложив их вместе, найти площадь полной поверхности треугольной призмы через боковое ребро и высоту основания. Объем треугольной призмы зависит той же площади основания и бокового ребра.
S_(б.п.)=3ab=3√2 hb
S_(п.п.)=3ab+(√3 a^2)/2=3√2 hb+√3 h^2
V=S_(осн.) b=(√3 a^2 b)/4=(√3 h^2 b)/2

Диагональ боковой грани треугольной призмы можно найти по теореме Пифагора из прямоугольного треугольника, в котором она является гипотенузой при катетах – боковом ребре и стороне основания.
d=√(a^2+b^2 )

В треугольную сферу можно вписать сферу, только если боковое ребро призмы совпадает с диаметром окружности, вписанной в основание, тогда радиус вписанной в треугольную призму сферы равен радиусу этой окружности. Радиус же описанной вокруг призмы сферы всегда равен корню из пяти шестых, умноженному на сторону основания призмы, поскольку описать такую сферу можно вокруг любой треугольной призмы.
r_1=r
R_1=√(5/6) a=√(5/3) h

Источник

Как найти сторону сечения прямой призмы

Прямая призма — многогранник с двумя параллельными основаниями-многоугольниками и боковыми гранями, лежащими в плоскостях, перпендикулярных основаниям.

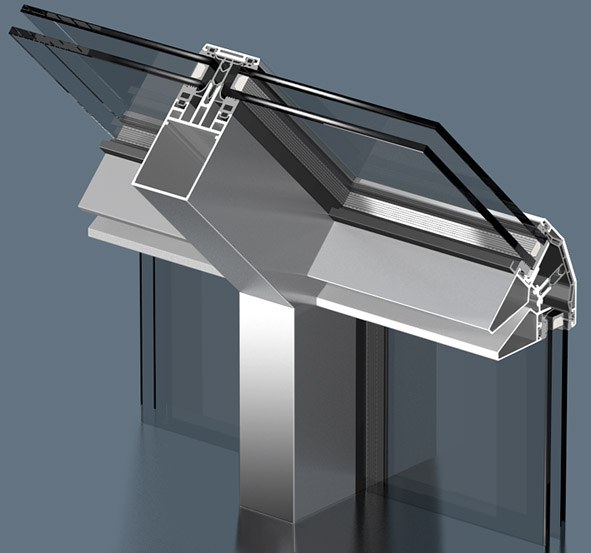
Инструкция

Основаниями прямой призмы являются равные друг другу многоугольники. Боковые ребра призмы соединяют вершины верхнего и нижнего многоугольника и перпендикулярны плоскостям оснований. Следовательно, боковые грани прямой призмы являются прямоугольниками. Эти прямоугольники образованы каждый двумя боковыми ребрами призмы и двумя сторонами фигуры основания (верхнего и нижнего).

Сечение призмы плоскостью, параллельной основаниям, образует фигуру, равную основанию. Все стороны такого сечения известны или определяются в процессе решения многоугольника.

Сечение призмы плоскостью, перпендикулярной основаниям, образует в пределах многогранника прямоугольник. Две стороны прямоугольника в этом сечении равны боковым ребрам призмы. Две другие стороны сечения лежат в плоскостях оснований и являются диагоналями многоугольников, если соединяют вершины фигуры оснований. Либо рассматриваемые стороны сечения могут соединять произвольные точки на сторонах многоугольника. Тогда для их нахождения необходимо провести в многоугольнике основания вспомогательные линии так, чтобы искомая сторона сечения стала стороной треугольника, в две другие стороны являются сторонами основания призмы. Нахождение неизвестной стороны сечения сводится к решению треугольника.

Сечение призмы плоскостью, расположенной под произвольным углом к основаниям и пересекающей плоскости оснований за пределами многогранника, является многоугольником с числом сторон, равным числу сторон основания. Каждую сторону образовавшейся в сечении фигуры нужно находить отдельно. Искомые стороны этого произвольного сечения делят каждую боковую грань прямой призмы на две прямоугольные трапеции. Отрезки боковых ребер призмы являются параллельными основаниями трапеций, сторона основания в трапеции является стороной и одновременно высотой. Искомая сторона сечения в каждой трапеции является четвертой стороной. Таким образом, задача нахождения сторон сечения прямой призмы произвольной наклонной плоскостью сводится к вычислению стороны прямоугольной трапеции.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Правильная четырехугольная призма

Определение.

Правильная четырехугольная призма — это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники

Боковое ребро — это общая сторона двух смежных боковых граней

Высота призмы — это отрезок, перпендикулярный основаниям призмы

Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани

Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра

Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник

Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам

Элементы правильной четырехугольной призмы

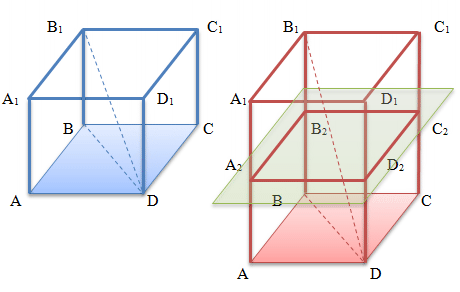
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:

Основания ABCD и A₁B₁C₁D₁ равны и параллельны друг другу
Боковые грани AA₁D₁D, AA₁B₁B, BB₁C₁C и CC₁D₁D, каждая из которых является прямоугольником
Боковая поверхность — сумма площадей всех боковых граней призмы
Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
Боковые ребра AA₁, BB₁, CC₁ и DD₁.
Диагональ B₁D
Диагональ основания BD
Диагональное сечение BB₁D₁D
Перпендикулярное сечение A₂B₂C₂D₂ .

Свойства правильной четырехугольной призмы

Основаниями являются два равных квадрата
Основания параллельны друг другу
Боковыми гранями являются прямоугольники
Боковые грани равны между собой
Боковые грани перпендикулярны основаниям
Боковые ребра параллельны между собой и равны
Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
Углы перпендикулярного сечения — прямые
Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное (ортогональное сечение) параллельно основаниям

Формулы для правильной четырехугольной призмы

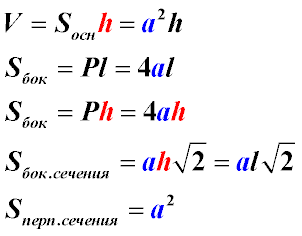
Указания к решению задач

При решении задач на тему «правильная четырехугольная призма» подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия — призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .

Задача.

В правильной четырёхугольной призме площадь основания 144 см², а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна

√144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 12² + 12² ) = √288 = 12√2

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )² + 14² ) = 22 см

Ответ: 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

a² + a² = 5²
2a² = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

h² + 12,5 = 4²
h² + 12,5 = 16
h² = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

S = 2a² + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см² .

Ответ: 25 + 10√7 ≈ 51,46 см² .

15306.1214

Прямая призма |

Описание курса

| Куб

Источник

Правильная шестиугольная призма

На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники .

Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.

Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.

Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) . Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.

Кратко: что представляет собой правильный шестиугольник?

Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .

*Противолежащие стороны параллельны.

Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?

У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.

То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.

Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.

*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.

272533. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 48. Найдите расстояние между точками A и E₁.

Рассмотрим прямоугольный треугольник AA ₁ E ₁ . По теореме Пифагора:

*Угол между сторонами правильного шестиугольника равен 120 градусам.

Отрезок АЕ ₁ является гипотенузой, АА ₁ и А ₁ Е ₁ катеты. Ребро АА ₁ нам известно. Катет А ₁ Е ₁ мы можем найти используя используя теорему косинусов.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

По теореме Пифагора:

*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 35. Найдите расстояние между точками B и E.

Рассмотрим правильный шестиугольник:

Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.

273353. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E₁.

Рассмотрим прямоугольный треугольник BB ₁ E ₁ . По теореме Пифагора:

Отрезок B ₁ E ₁ равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть

273683. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 45. Найдите тангенс угла AD₁D.

Рассмотрим прямоугольный треугольник ADD₁, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.

Рассмотрим правильный шестиугольник:

В нём углы между сторонами равны 120°. Значит,

Сама длина ребра не имеет значения, на величину угла она не влияет.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим прямоугольный треугольник AC₁C:

Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :

Значит, угол AC ₁ C равен 60 градусам.

274453. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим треугольник AС ₁ С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть

Катет С₁С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):

В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть

245364. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками А и Е₁.

245365. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками В и Е.

245366. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁все ребра равны корню из пяти. Найдите расстояние между точками В и Е₁.

245367. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите тангенс угла AD₁D.

245368. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.

245369. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите угол AC₁C. Ответ дайте в градусах.

На этом всё! Успеха Вам!

В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!

Правильная шестиугольная призма — свойства, признаки и формулы

Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
боковые рёбра — стороны, являющиеся общими для боковых граней;
вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.

Правильная шестиугольная призма — это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.

Основания призмы являются равными правильными шестиугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности шестиугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной шестиугольной призмы:

Правильная шестиугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной шестиугольной призмы:

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Источник