Где d — диагональ,b — сторона.
Где d — диагональ,α — угол между диагональю и искомой стороной.
Где d — диагональ,α — угол между диагональю и другой стороной.
Где S — площадь, b— известная сторона.
Где P — периметр, b — известная сторона.
Где d — диагональ, α — угол между диагоналями.
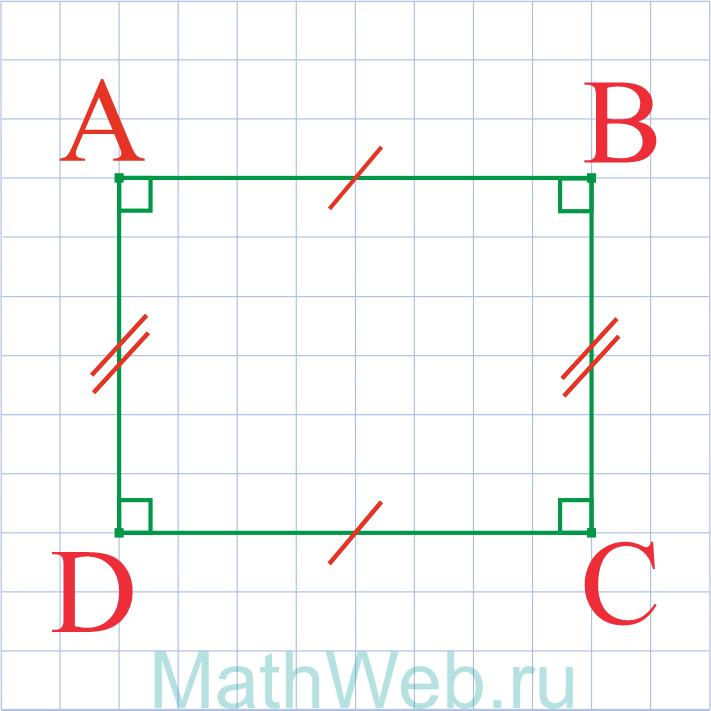
- Прямоугольник — это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
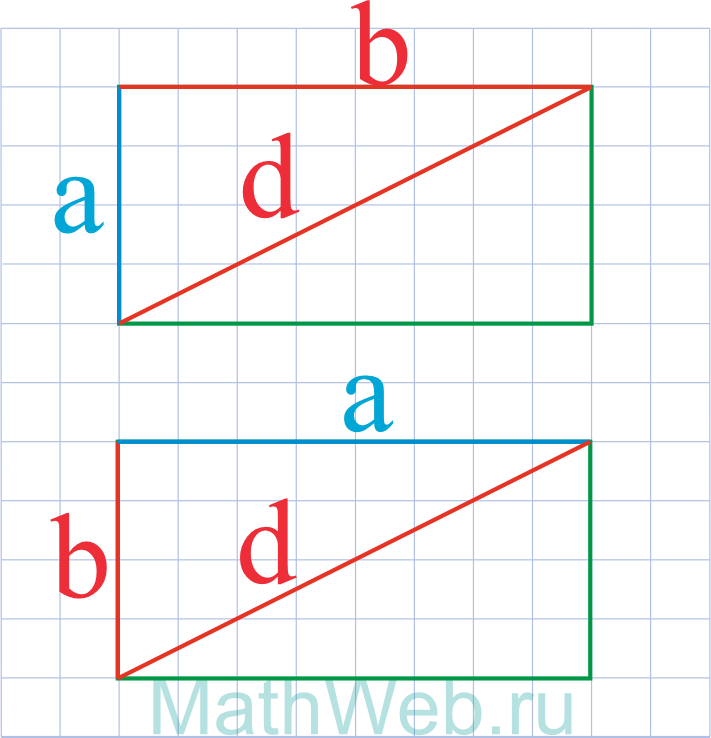 |
a = √d2 ― b2 |
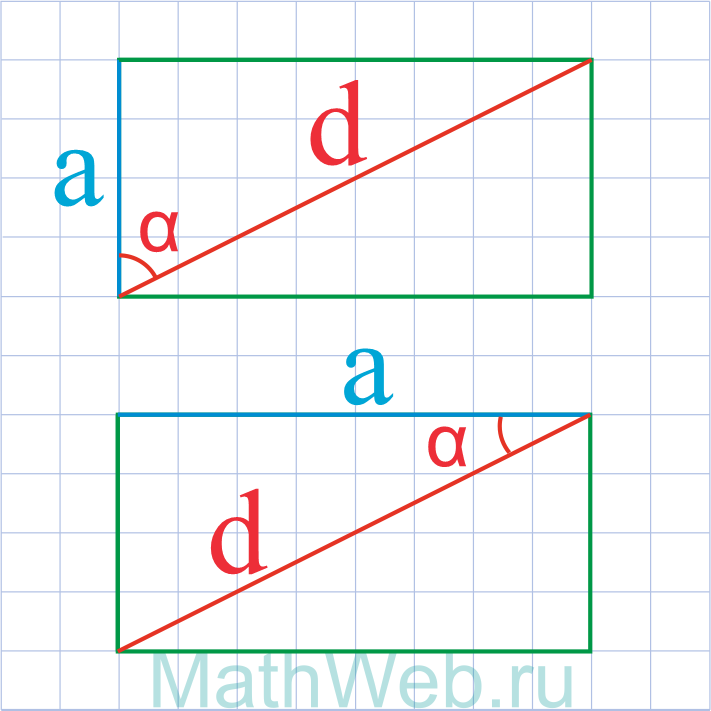 |
a = d·cos(α) |
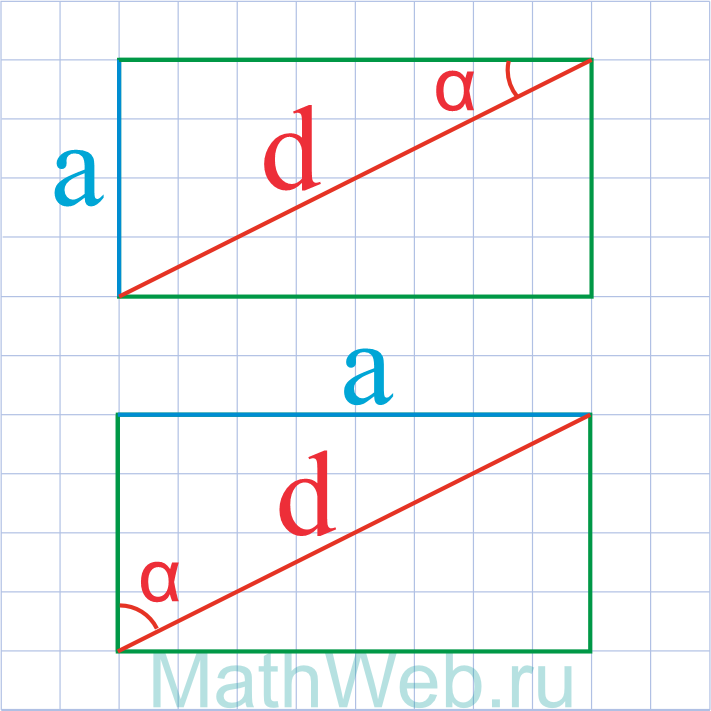 |
a = d·sin(α) |
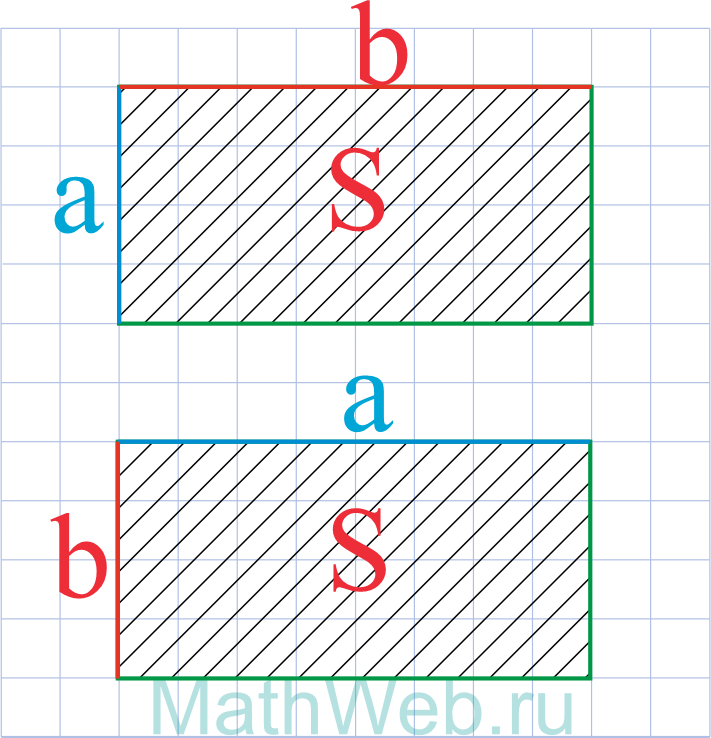 |
a = S b |
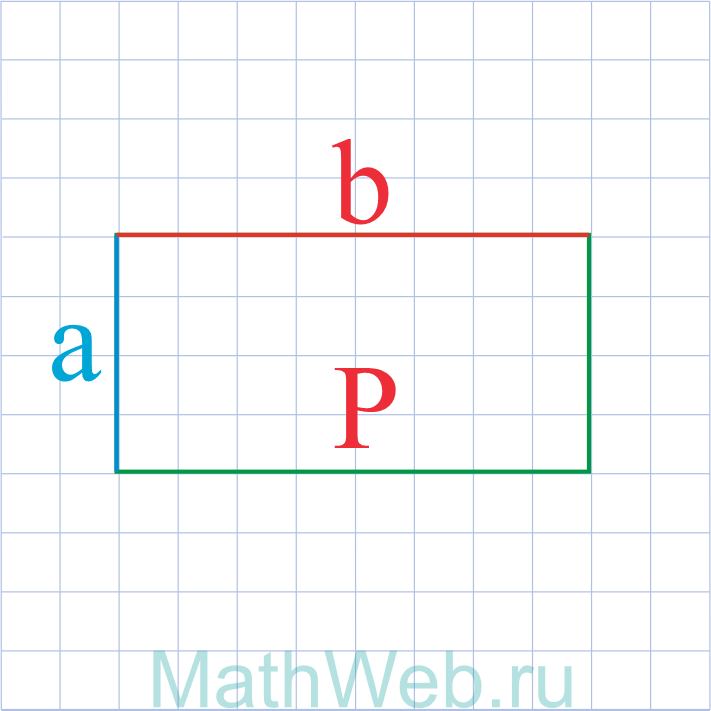 |
a = P — 2b 2 |
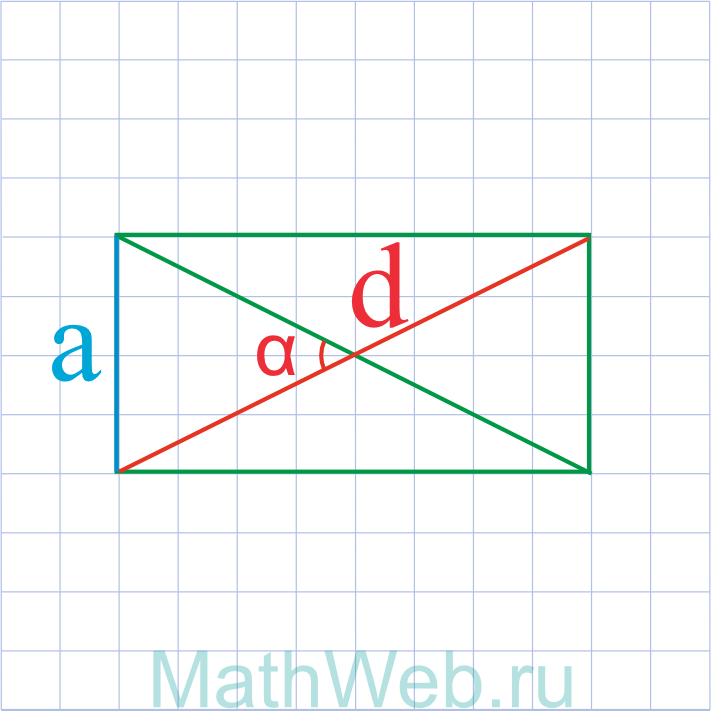 |
a = d·sin(0.5·α) |
Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.
- Сторона прямоугольника через диагональ и угол между
диагональю и стороной - Сторона прямоугольника через диагональ и известную
сторону - Сторона прямоугольника через площадь и другую известную
сторону - Сторона прямоугольника через периметр и другую известную
сторону - Сторона прямоугольника через диагональ и угол между
диагоналями
Через диагональ и угол между диагональю и стороной
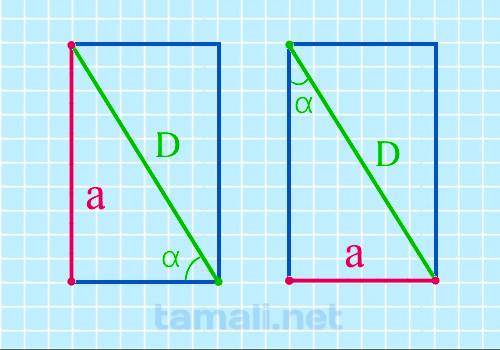
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:
a = d * sinα
где d — это диагональ, а, b — одна из сторон фигуры.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.
Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.
Через его площадь и известную сторону
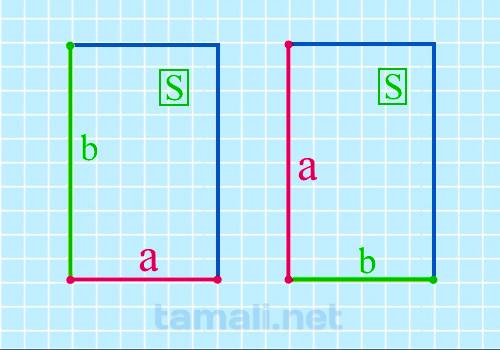
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно
a = S / b
где S — площадь прямоугольника, b — известная сторона.
Цифр после
запятой:
Результат в:
Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.
Через диагональ и известную сторону
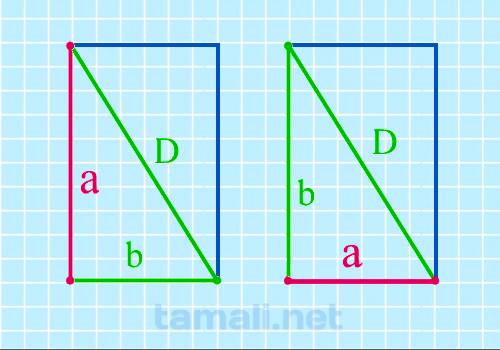
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :
a = √(d² — b²)
где d — диагональ, а, b — стороны.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.
Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
Через диагональ и угол между диагоналями
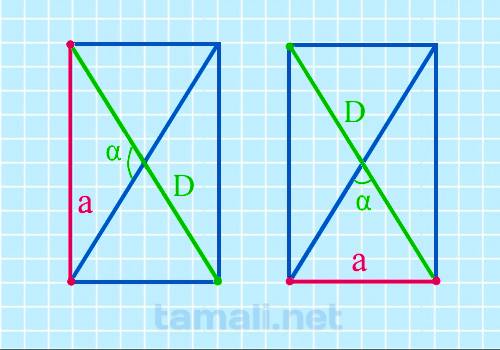
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:
a = D • sin(α/2)
где D — диагональ, α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.
Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.
Через периметр и другую известную сторону
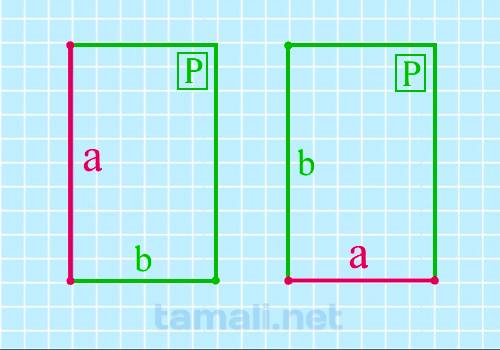
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).
a = (P — 2b) / 2
где P — периметр прямоугольника, b — другая известная сторона.
Цифр после
запятой:
Результат в:
Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.
Другие примеры по решению задач на прямоугольник с использованием длины и ширины
- Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов - Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см². - Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.
Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника являются равными и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма внутренних углов равна 360°.
- Диагонали пересекаются друг с другом.
- Длина диагоналей равна.
- Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2). - Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
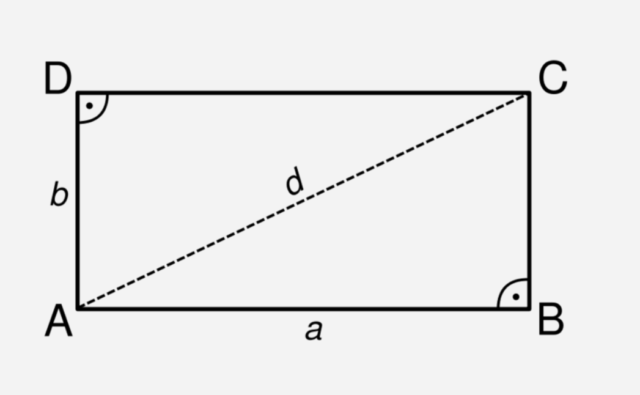
Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d2 = a2 + b2, а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:
2d2 = 2a2 + 2b2
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.

4.4
Средняя оценка: 4.4
Всего получено оценок: 200.
4.4
Средняя оценка: 4.4
Всего получено оценок: 200.
В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.
Длины прямоугольника
Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.
Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.
Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:
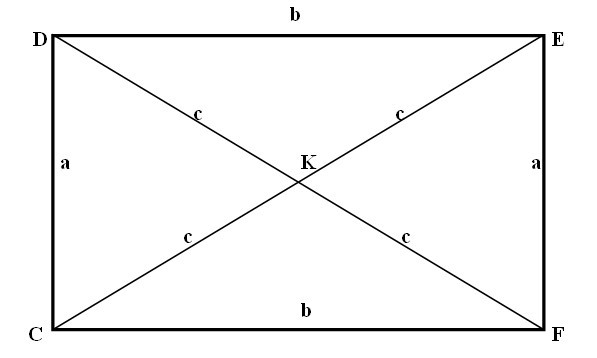
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
- Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.
Примеры решения задач
Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.
Задача 1
- Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.
Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:
$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)
$a*b=S$ (уравнение для нахождения площади)
При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.
Продолжим решение. Выразим значение a из первого выражения системы.
- $(а+b)*2=Р$
- $а+b={Рover{2}}$
- $а={Рover{2}}-b$
- Подставим значение периметра: $а={20over{2}}-b=10-b$
Подставим получившееся выражение в уравнение нахождения площади:
$a*b=S$
$(10-b)*b=21$
$b^2-10b-21=0$
Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.
$а=10-b$
Значит, при $b=3$, $а=10-3=7$
При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.
Задача 2
- Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.
Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).
Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.
$D^2=a^2+b^2$
$A^2=d^2-b^2$
$а^2=400-256=144$
Корень квадратный из 144 равен 12. Это и есть ответ к задаче.
Задача 3
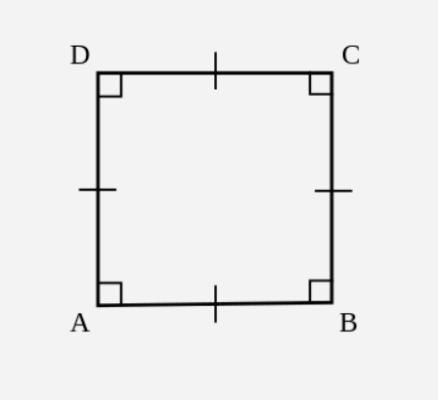
- Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.
У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.
Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.
$а^2=S$
$а^2=25$
$а=5$
Что мы узнали?
Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 200.
А какая ваша оценка?
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
Кроме этого:
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
или
Из равенства (1) найдем d:
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
Ответ:
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
Подставляя (3) в (2), получим:
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
Действительно.
Тогда
Имеем ( small sqrt{D} <2d ,) ( small P > 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

Подставляя значения 

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

Ответ: 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.