Как найти сторону равностороннего треугольника через медиану

Узнать ещё

Знание — сила. Познавательная информация

По сторонам и медиане найти сторону треугольника

Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.

По двум сторонам и медиане найти третью сторону треугольника — задача, обратная нахождению медианы треугольника по трем его сторонам .

Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.

Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.

На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.

Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.

Переходим к решению конкретной задачи.

По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.

Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.

Найти сторону треугольника через медиану и стороны

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

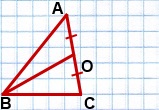
BO — медиана, BO=√46 см.

1) На луче BO отложим отрезок OD,

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

Определение и свойства медианы равностороннего треугольника

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S₁ = S₂.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

• BG = 8 см (самая большая сторона, является гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Равносторонний или, как ещё говорят, правильный треугольник — удивительная фигура. Ведь только в ней совпадают медиана, высота, биссектриса и серединный перпендикуляр. Знание этих и других свойств зачастую избавляет нас от использования сложных и порой очень громоздких вычислений.

Так, например, точка пересечения всех выше перечисленных отрезков делит их в соотношении 1/2 (DO/BO = EO/CO = FO/AO = 1/2). Как это можно использовать для решения нашей задачи? А вы посмотрите на треугольник ∆BOF — его гипотенуза составляет 2/3 от известного значения 9√3, а меньший катет — 1/3. Разобраться со вторым катетом не составит большого труда:

• BF = √(BO² — OF²) = √((9√3*2/3))² — (9√3*1/3))²) = √((6√3)² — (3√3)²) = 12 — 3 = 9

Но это лишь половинка стороны треугольника. Стало быть, потребуется её удвоить, чтобы получить целую:

• BC = 2 * BF = 2 * 9 = 18

Казалось бы, всё не так уж сложно. К тому же, существуют и иные способы вычисления. Но наше поколение, которое училось в школе и вузах в 70-80-х, по сей день больше полагается на шпаргалки. И у меня таких есть немножко. Одна из подходящих сразу выдаёт несколько разных формул, которые связывают между собой стороны и высоты, радиусы вписанных и описанных окружностей. Не поверите, но там есть и формула прямой зависимости высоты правильного треугольника от длины его стороны.

В таком случае мы можем записать:

• 9√3 = a√3/2 из чего следует, что
• a = 9√3 * 2 / √3 = 9 * 2 = 18

Тут, как говорится в известной поговорке, всё гениальное просто. Не я это придумал, но грех не воспользоваться при удобном случае такой формулой. И она лишний раз подтверждает, что правильный ответ:

• AB = BC = CA = 18

Всё! Удачи на дорогах!

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!