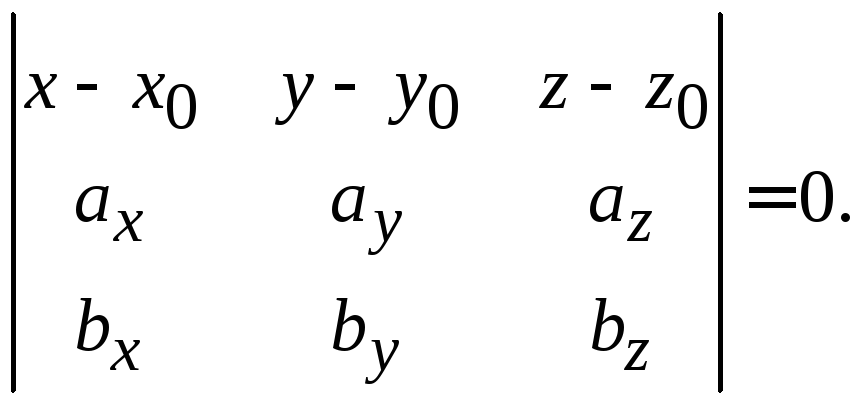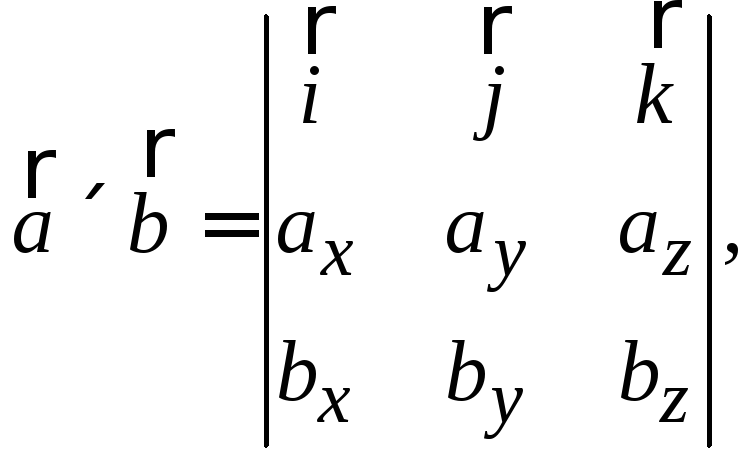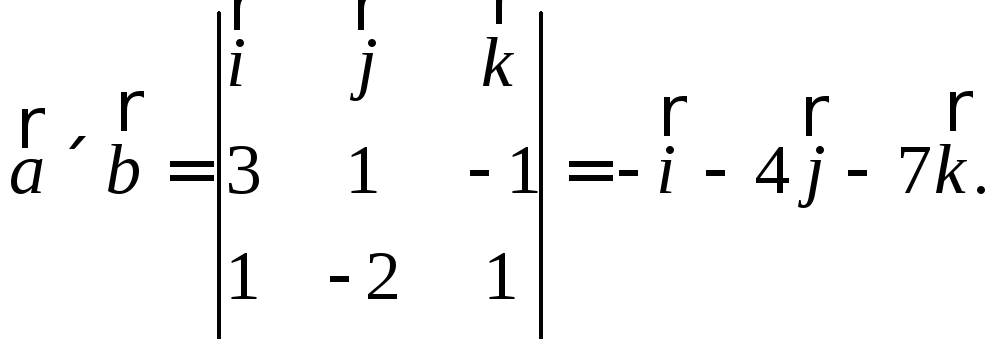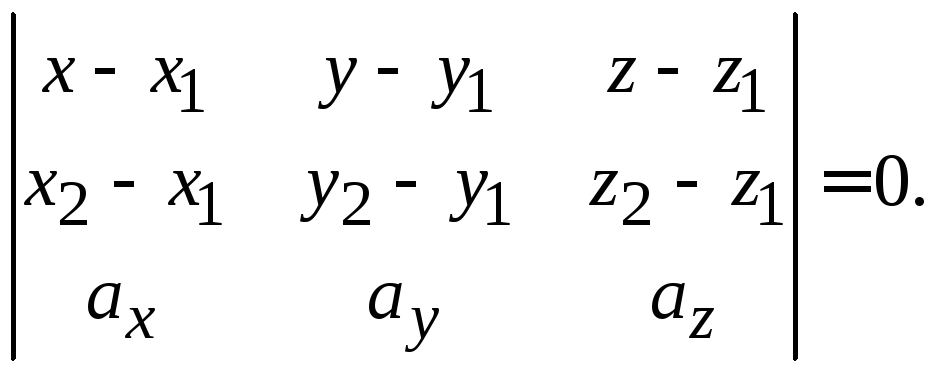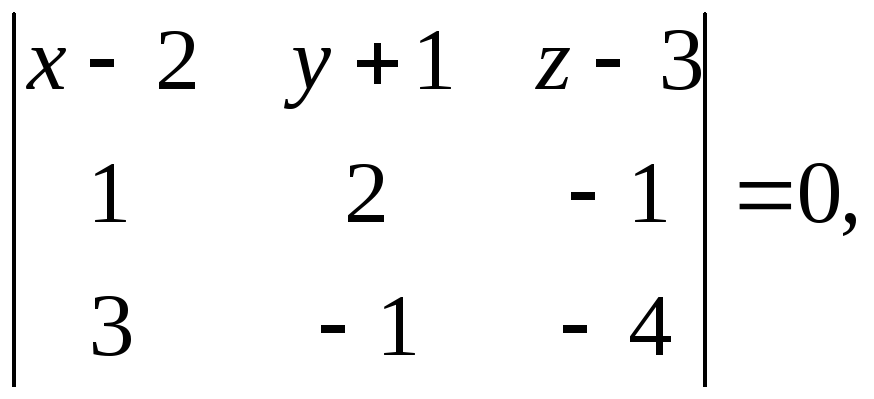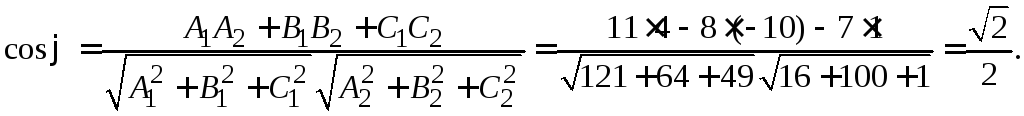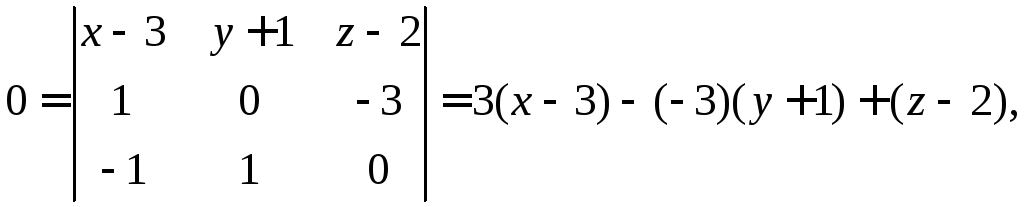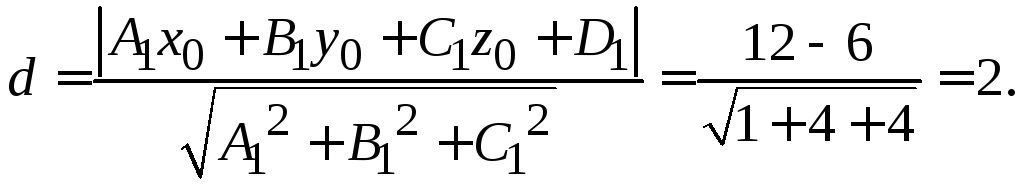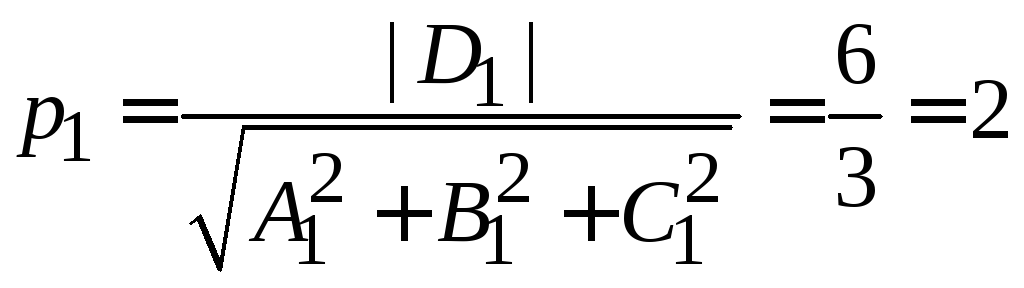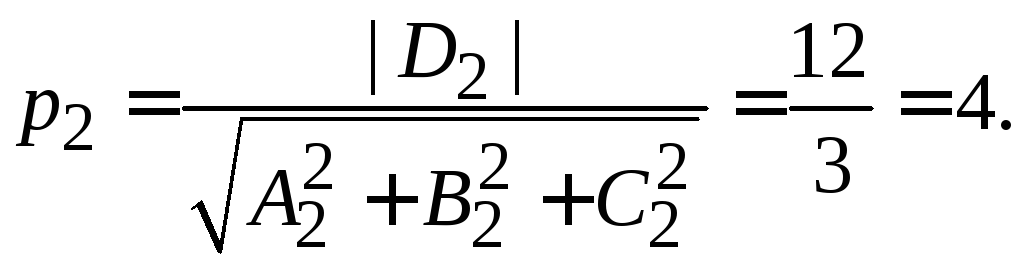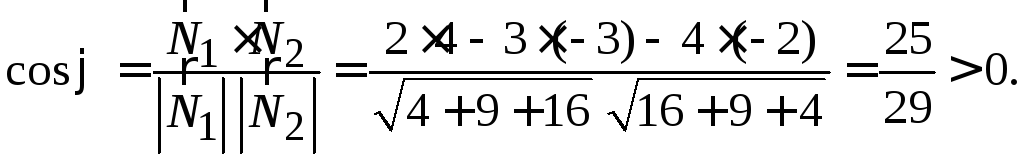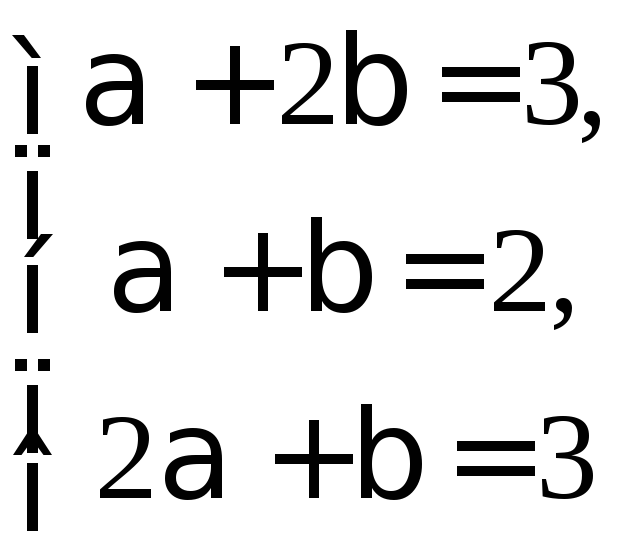Как найти сторону тетраэдра если даны вершины

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Написать уравнение стороны ас и высоты тетраэдра

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Как найти высоту тетраэдра формула Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра (h — высота тетраэдра, a — ребро тетраэдра)

Вывод формулы высоты тетраэдра

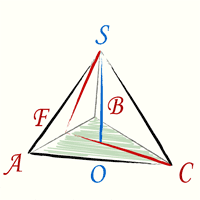
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

• S – площадь любой грани,
• H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

• Все грани равны.
• Все плоские углы правильного тетраэдра равны 60°
• Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
• Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Свойства

Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h

Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2

Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2

Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)

Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8

В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4

Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)

Краткая теория

---

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды 
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

 найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

Угол между ребрами

 и

 найдем как угол
между направляющими векторами

  и

:

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

 и гранью

.

Для этого вычислим
координаты нормального вектора плоскости

 –им будет
векторное произведение векторов 

 и

.

 

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

  

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

    и 

:

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

  и

:

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

.  Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

 

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

 -уравнение
грани

 

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

 из вершины

:

Нормальный вектор

 является
направляющим вектором высоты, кроме того, высота проходит через точку

 

Искомое уравнение
высоты:

Сделаем схематический чертеж:

1) Найдем длину стороны AC:
2) Найдем координаты векторов и :
Найдем модули векторов:
,
3) Найдем координаты середины стороны AC:
; ; .
Найдем длину медианы BM:
Найдем координаты середины стороны AD:
; ; .
Найдем длину медианы BN:
Найдем координаты середины стороны CD:
; ; .
Найдем длину медианы BO:
4) Найдем уравнение плоскости ACD:
Получаем уравнение плоскости: .
Уравнение перпендикуляра, к плоскости ACD, проходящего через точку B:
или
Найдем точку пересечения прямой и плоскости
. Для этого подставим координаты перпендикуляра в уравнение плоскости:
Откуда: , тогда точка пересечения: .
Найдем длина высоты из вершины B:
5) Найдем длины сторон тетраэдра:
Найдем косинусы углов:
Найдем косинусы половины углов:
Найдем длину биссектрисы к стороне AC:
Найдем длину биссектрисы к стороне AD:
Найдем длину биссектрисы к стороне CD:
6) Найдем уравнение медианы BM:
или
Найдем середину стороны BC:
; ; .
Найдем уравнение медианы AN:
или
Найдем точку пересечения медиан:
Откуда , тогда точка пересечения .
7) Найдем произведение векторов и :
Площадь треугольника ABC:
Объем тетраэдра ABCD:
Ответ: 1) ; 2) 165,6°; 3) медиана к стороне AC: , к стороне AD: 5, к стороне СD: ; 4) ; 5) длина биссектрисы к сторону AC: 4,498, к стороне AD: 4,983, к сторону CD: 3,513; 6) ; 7) ; .

1. Решение типовых задач

Задача 1.1. Составить
уравнение плоскости, проходящей через
точку

,если задан нормальный вектор.

Р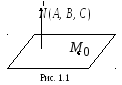ешение.Воспользуемся уравнением (1.2):

Подставляя координаты вектора
и точки,
получим

Ответ:

Задача 1.2. Составить уравнение
плоскости, проходящей через точкупараллельно векторами(их называют направляющими векторами
плоскости).

Решение.

П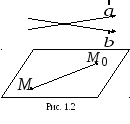ервый
способ.Пусть– ­произвольная точка на плоскости.Тогда векторы


и(рис. 1.2) должны быть компланарны, т. е.
их смешанное произведение должно быть
равно 0:.Запишем смешанное произведение через
координаты векторов. Получим

Подставим заданные координаты и вычислим
определитель разложением по элементам
первой строки:

,

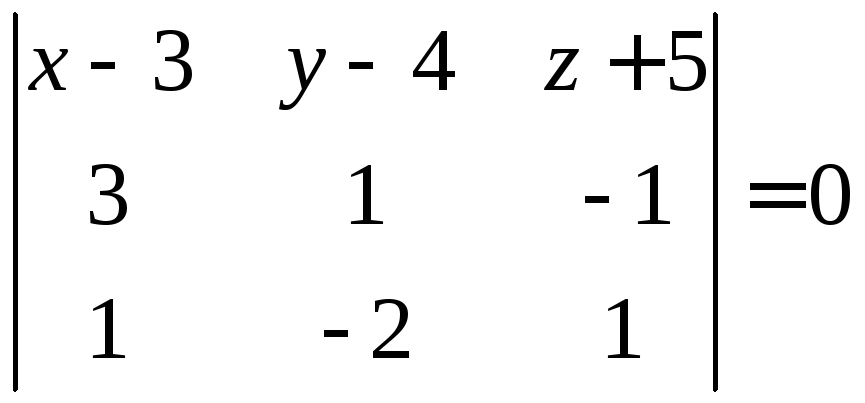
или

.

Окончательно:

Второй способ. Найдем сначала вектор(рис. 1.1). Очевидно, что вектор
нормали
к плоскости должен быть ортогонален
также векторами.
Поэтому его можно выбрать как
векторное произведение

Затем выпишем общее уравнение плоскости,
используя
,(см.
формулу (1.2)). Получим

Ответ:

Полезная
формула. Если
плоскость проходит через точку
,
и– ее направляющие векторы, то уравнение
плоскости имеет вид

(1.7)

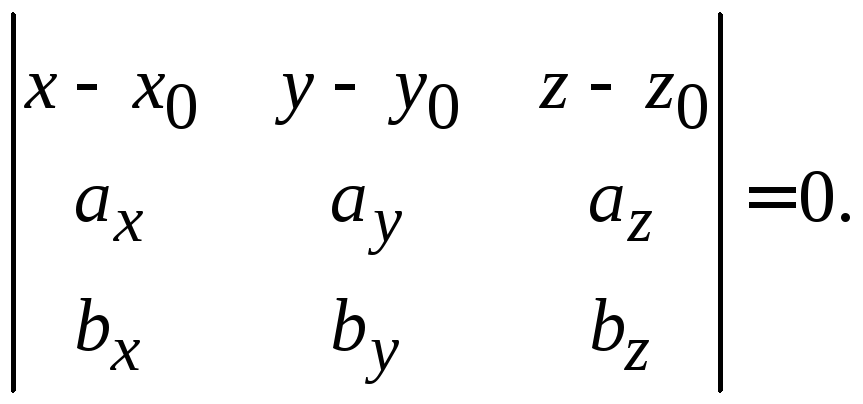
Замечание.Первый способ решения
задачи предпочтительнее. Второй способ
отличается лишь тем, что в нем смешанное
произведение трех векторов,,вычисляется последовательно. А именно:
сначала находим векторное произведениеи затем результат умножаем скалярно на
вектор.
В дальнейшем при решении задач будем
придерживаться первого способа.

Задача 1.3. Составить уравнение
плоскости, проходящей через точкиипараллельно вектору.

Р

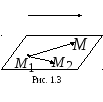
ешение.Пусть
произвольная точка на плоскости.
Тогда векторы,икомпланарны (рис. 1.3). Запишем условие
компланарности векторов через их
координаты:

Подставляя заданные координаты, получим

или

Окончательно:

Ответ:

Полезная
формула.Если плоскость проходит
через две заданные точкиипараллельно вектору,
то ее уравнение имеет вид

(1.8)

Задача 1.4. Составить уравнение
плоскости, проходящей через точкупараллельно плоскости

Решение. В качестве вектораискомой плоскости можно выбрать
нормальный вектор заданной плоскости,
так как эти плоскости параллельны. Таким
образом, имееми.
Подставляя координатыив уравнение (1.2), получим

Окончательно:

Ответ:

Задача 1.5. Найти величину острого
угла между плоскостямии

Решение. Угол между плоскостями
равен углу между нормальными векторамии(см. формулу 1.4)).

Отсюда

Ответ:

Задача 1.6. Чему равен угол между
плоскостямии?

Решение. Найдем скалярное произведение
нормальных векторов
и

Следовательно, эти плоскости
перпендикулярны:

Ответ:

Задача 1.7. Составить уравнение
плоскостей, которые проходят через
точкуи отсекают на координатных осях отличные
от нуля отрезки одинаковой длины.

Р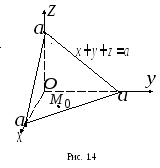ешение.Воспользуемся уравнением плоскости
в отрезках на осях (1.3). Рассмотрим сначала
случай 1:(рис. 1.4). Тогда
получим

Подставляя в уравнение координаты точки
,
найдем

Уравнение плоскости:

Затем следует
аналогично рассмотреть случаи 2:
3:
4:
Получим четыре различные плоскости.

Ответ:

Задача 1.8. Построить
плоскости, заданные уравнениями: 1);2)
;
3)
;
4) плоскость,
проходящую через точкупараллельно плоскости;
5) плоскость,
проходящую через точкуи ось.

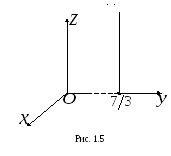
Решение.1. Плоскостьпараллельна плоскостии отсекает на осиотрезок,
равный
(рис. 1.5).

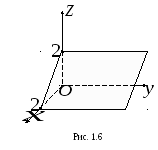
2. Плоскость
параллельна оси,
пересекает плоскость
по прямой

,
отсекая на осяхиотрезки, равные 2 (рис. 1.6).

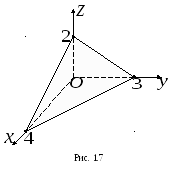
3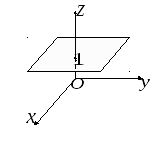. Уравнение
плоскости запишем в отрезках на осях
(1.3):.
Плоскость отсекает на осях,,отрезки, длины которых равны соответственно
4, 3, 2 (рис. 1.7).

Рис. 1.8

4. Так как плоскость
параллельна плоскости,
то ее нормальный вектор можно выбрать
в виде.
Тогда согласно формуле (1.2) уравнение
плоскостибудет,
гдепо условию задачи. Таким образом, получаем(рис. 1.8).

5.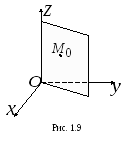
Плоскостьпроходит через ось.
Поэтому ее нормальный вектор имеет вид.
Так как плоскость проходит через начало
координат,
то коэффициент
в уравнении
плоскости (1.1) равен 0. Подставляя
координаты точки
в уравнение,
получаем(рис. 1.9).

Задача 1.9. Составить уравнение
плоскости, проходящей через три заданные
точки

Р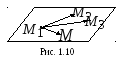ешение.Пусть
произвольная
точка на плоскости. Тогда векторы,,компланарны (рис. 1.10). Запишем условие
компланарности этих векторов через их
координаты:

Подставим
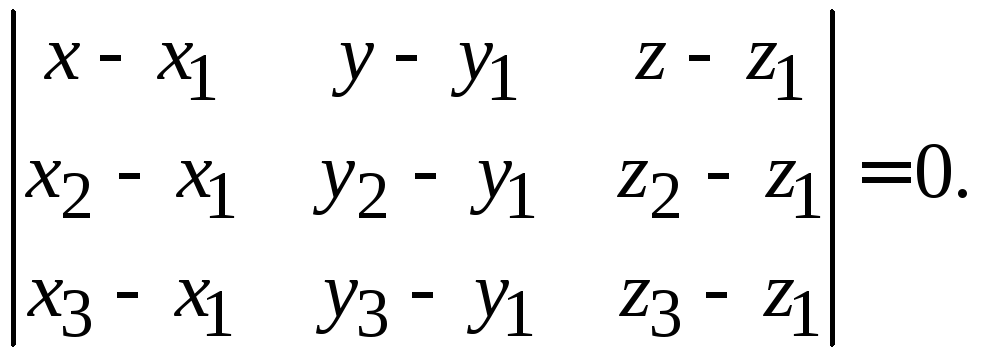
значения координат и найдем уравнение
плоскости:

или

Ответ:

Полезная
формула. Если плоскость проходит
через три заданные точкине лежащие на одной прямой, то ее уравнение
имеет вид

(1.9)

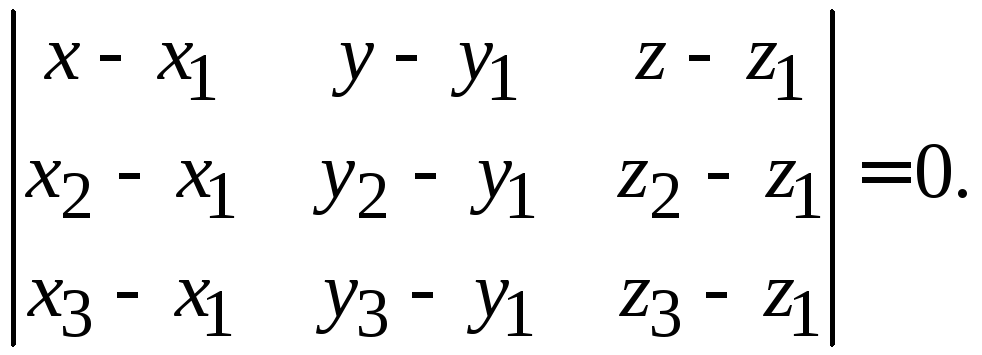
Задача 1.10. Даны
координаты вершин тетраэдра:
,,,(рис. 1.11). Составить уравнения его граней.

Р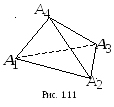ешение.Найдем уравнение грани.
Для этого подставим в формулу (1.9)
координаты вершин:

,

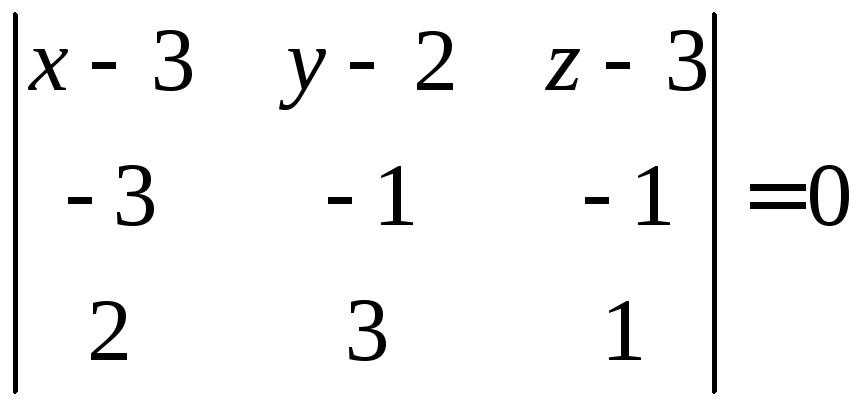
или

.

Уравнение искомой грани имеет вид

Уравнения
граней
,,найдите самостоятельно.

Ответ:

.

Задача 1.11. Найти расстояние от точкидо плоскости

Решение. Используем формулу (1.5):.

Ответ:

Задача 1.12. Найти расстояние между
параллельными плоскостями

.

Решение.

Первый способ.
Выберем
произвольно точку

на плоскости
.
Пусть, например,ТогдаСледовательно,Найдем расстояниеот
точкидо плоскости,
по формуле (1.5):

Второй
способ.Очевидно, что плоскостиилежат по одну сторону относительно
начала координат

Обозначим через
расстояние от начала координат
до плоскости,
через– до плоскости(рис. 1.12).

,

Расстояние между плоскостями равно
.
Отсюда находим

Ответ:

Замечание. Если бы плоскости
находились по разные стороны от начала
координат (рис. 1.13), то расстояние между
ними было бы равно

Задача 1.13. Составить уравнение
плоскости, проходящей через заданную
прямуюи точкуне лежащую на этой прямой.

Решение. Уравнение произвольной
плоскости,
проходящей через заданную прямую, имеет
вид (см. формулу (1.6))

Отсюда

:

Подставляя в это уравнение координаты
точки
,
получим

,

Положим, например,
ТогдаОстается подставить эти коэффициенты
в уравнение плоскости. Получим

Ответ:

Задача 1.14. Написать уравнение
биссектрисыострого двугранного угла между плоскостямии

Решение. Нормальные
векторы первой и второй плоскостей
соответственно равны
иОни образуют острый угол,
так как

Очевидно, что
(Нормальные векторыивсегда можно взять равными по длине,
например, единичными.) Так как,
то параллелограмм, построенный на
векторахикак на сторонах, является ромбом, а
диагональбиссектрисой его угла. Следовательно,
векторможет быть выбран в качестве нормального
вектора искомой биссектрисыДалее следуем рассуждениям задачи 1.13.
Уравнение биссектрисыищем в виде

Отсюда

Учитывая, что
получаем систему уравнений

Подставляя эти значения в уравнение
биссектрисы
,
имеем

Окончательно:

Чертеж к этой задаче предлагаем сделать
самостоятельно.

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #