Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
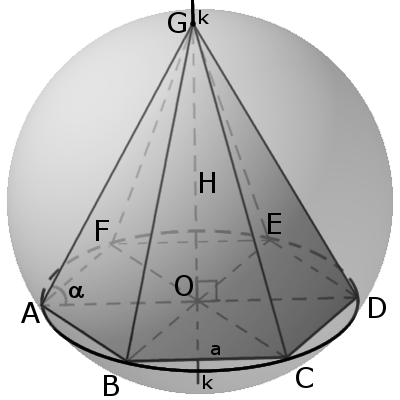
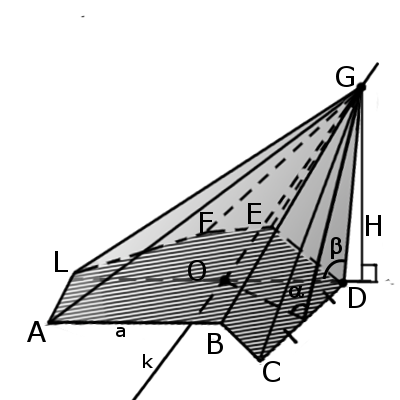
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
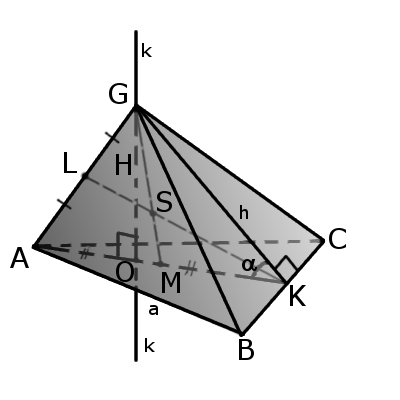
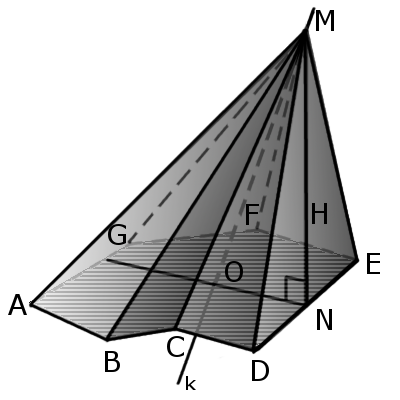
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
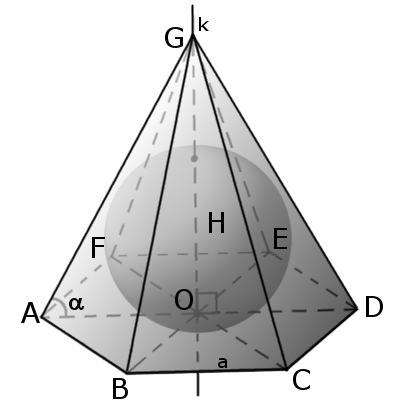
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))
Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса — треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
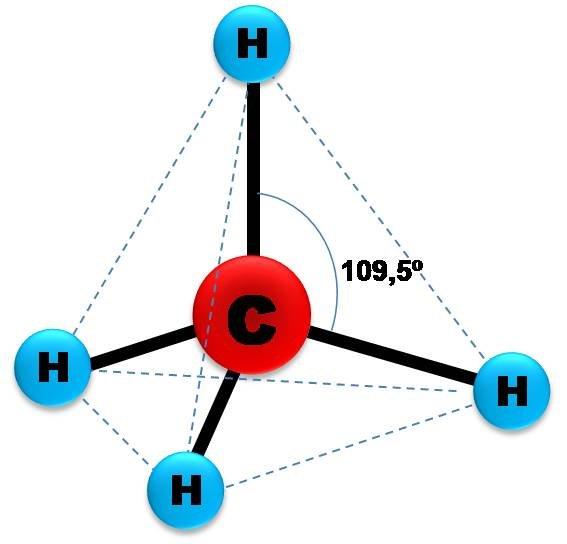
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней — это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
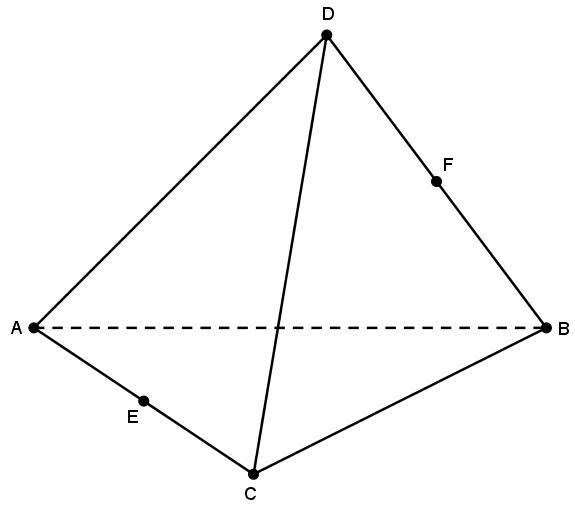
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
h = √(b2 — a2/3)
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
ab = √(b2 — a2/4)
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
V = 1/3*So*h
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
V3 = √3/12*a2*h
Где высота правильной треугольной пирамиды равна h, а ее сторона основания — a.
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
V = √2/12*a3
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
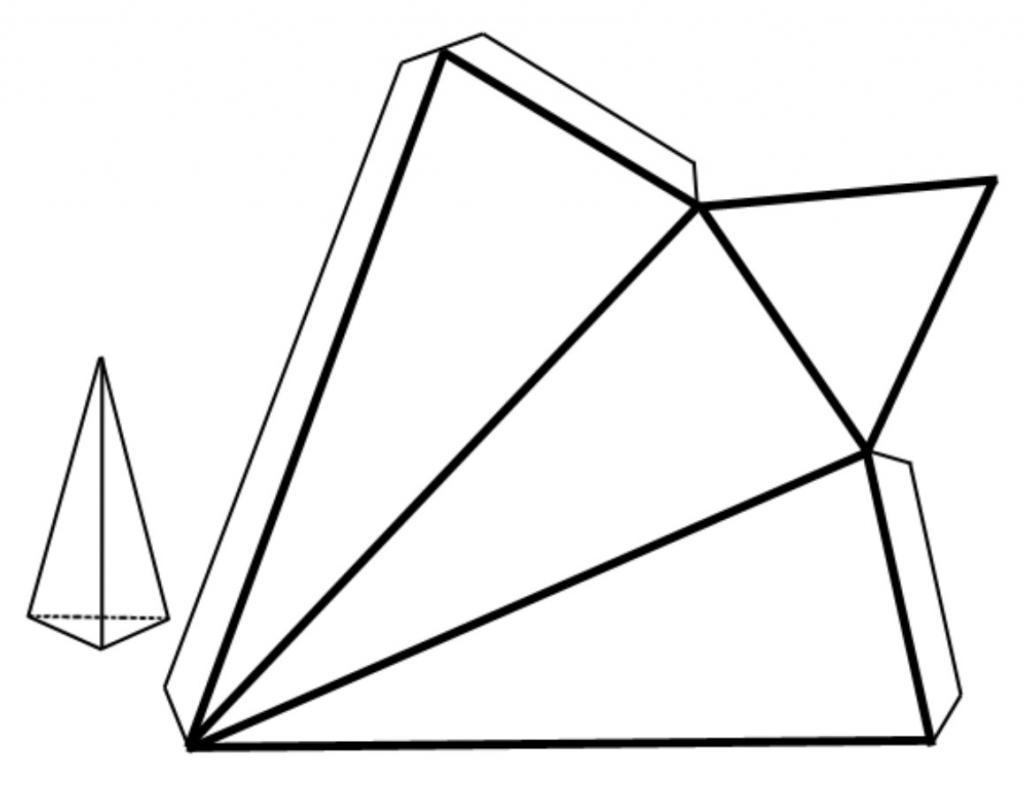
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
So = √3/4*a2
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Sb = 3/2*√(a2/12+h2)*a
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
S = √3*a2
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
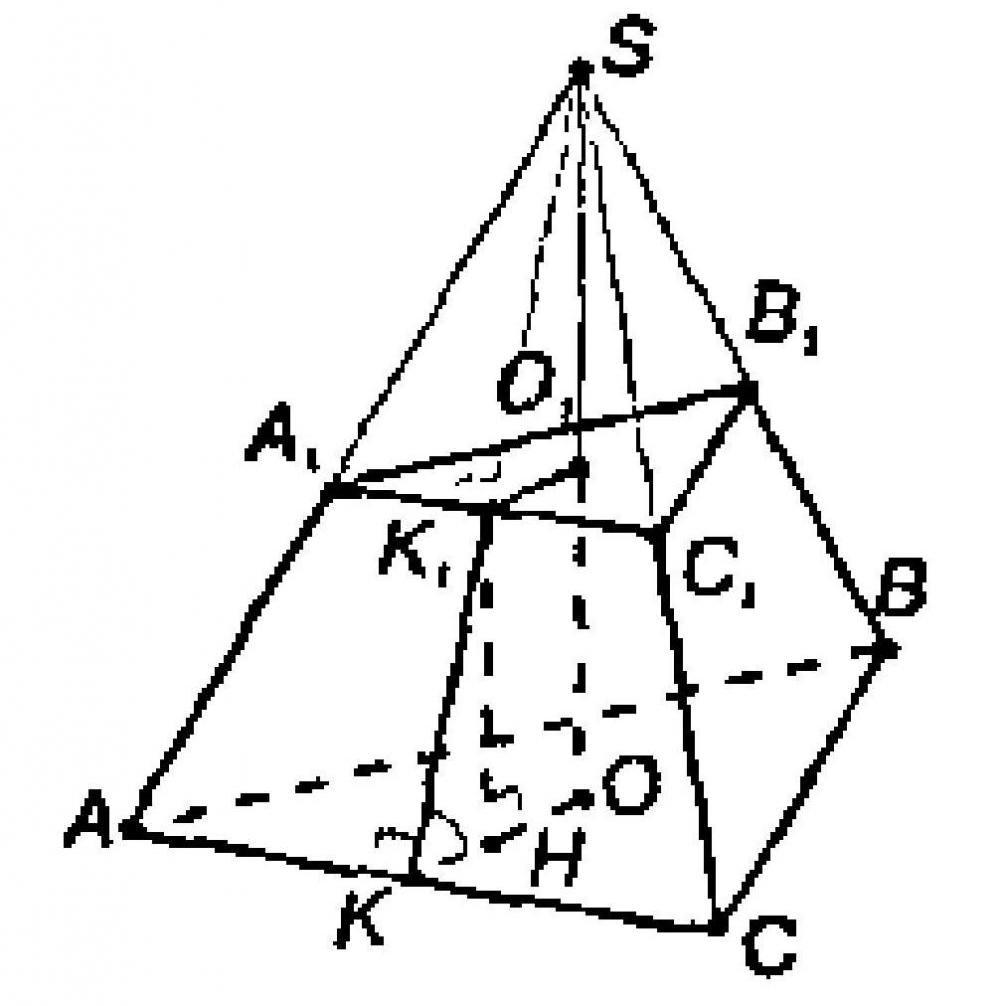
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Здесь первое слагаемое — это площадь боковой поверхности, второе слагаемое — площадь треугольных оснований.
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Пирамида – это объемная многогранная геометрическая фигура, состоящая из основания и треугольных
граней, собирающихся в одной точке. У нее есть: вершина, ребра (боковые и основные), боковые грани,
основание, высота и апофема – прямая, соединяющая вершину с границей вписанной в основание
окружности. Правильная пирамида –та, у которой все боковые ребра равны и находятся под одним углом к
основанию, а вершина проецируется на центр окружности, описанной вокруг основания. Тетраэдр –
частный случай правильной пирамиды, в которой боковые ребра равны основным и между собой.
Боковые ребра правильной пирамиды – выходящие из ее вершины, общие для боковых граней стороны. Длина
бокового ребра обозначается латинской буквой «b». Это одно из базовых значений, через которое можно
найти остальные элементы пирамиды. Во многих математических задачах требуется вычислить его или
подставить в формулы.
- Боковое ребро правильной треугольной пирамиды через высоту
и ребро основания - Боковое ребро правильной треугольной пирамиды через высоту
и радиус описанной окружности вокруг правильной треугольной пирамиды - Ребро основания правильной треугольной пирамиды через обьём
и высоту
Ребро основания правильной треугольной пирамиды через объём и высоту
Та часть пространства, которую занимает правильная треугольная пирамида называется ее объемом.
Является физической величиной. Его можно найти через, например, через высоту и сторону основания.
Если нам известен объем и высота правильной треугольной пирамиды, то не составит особого труда найти
ребро основания. Для этого используется формула:
a = √((V * 4 * √3) / H)
где V — объём, H — высота.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретную задачу. Необходимо найти ребро основания, зная что
высота H равна 56 см, a объем 268 см³, подставив все в формулу получим следующий результат: a = √((V * 4 * √3) / H) = √((268 * 4 * √3) / 56) = 5,76 см. Боковое
ребро (b) = 5,76 см.
Боковое ребро правильной треугольной пирамиды через высоту и ребро основания
Боковое ребро правильной пирамиды можно найти по теореме Пифагора, поскольку высота, опущенная в
основание пирамиды, опускается в центр вписанной и описанной окружности для данного многоугольника.
Таким образом формула для нахождения бокового ребра правильной треугольной пирамиды через высоту и
ребро основания будет следующей:
b = √(H² + (a / 2 sin (60º)²))
где H — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 44 мм, a ребро основания
a равно 63 мм, подставив все в формулу получим следующий результат: b = √(H² + (a / 2 sin (60º)²)) = √(44² + (63 / 2 sin (60º)²)) = 57,09 мм.
Боковое ребро (b) = 57.08765 мм.
Боковое ребро правильной треугольной пирамиды через высоту и радиус описанной окружности вокруг
правильной треугольной пирамиды
Если пирамида вписана в окружность, то ее называют описанной вокруг пирамиды. Около пирамиды можно
описать сферу тогда и только тогда, когда около основания пирамиды можно описать
окружность. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее
основания, является центром описанной около основания окружности. Если нам известна высота и радиус
этой описанной окружности, то мы сможем найти боковое ребро. Формула подходит только для правильной
треугольной пирамиды:
b = √(H² + R²)
где H — высота правильной треугольной пирамиды, R — радиус описанной вокруг
окружности.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 73 мм, a радиус описанной
вокруг окружности 114 мм, подставив все в формулу получим следующий результат: b = √(H² + R²) = √(73² + 114²) = 135 мм. Боковое
ребро (b) = 135 мм.
Почти все формулы пирамиды основываются на теореме Пифагора. Таким образом, можно вывести боковое
ребро правильной треугольной пирамиды через высоту и радиус описанной окружности, опираясь на
прямоугольный треугольник, гипотенуза которого является искомой величиной. По одному из основных
свойств правильной пирамиды, ее высота соединяет вершину с центрами окружностей, вписанных и
описанных вокруг пирамиды. Так внутри формируются 2 треугольника с углом 90°. Один состоит из
высоты, бокового ребра и соединяет их с радиусом описанной окружности, другой составляет высота и
апофема, соединённые с радиусом вписанной окружности.
Пирамида. Формулы и свойства пирамиды
Определение.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
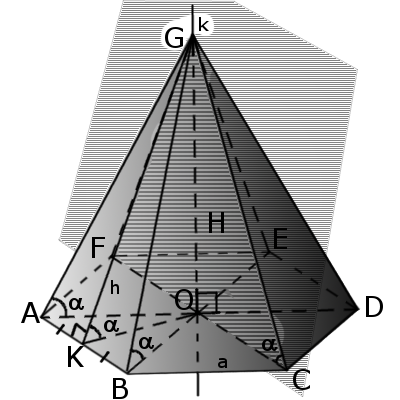 |
| Рис.1 |
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
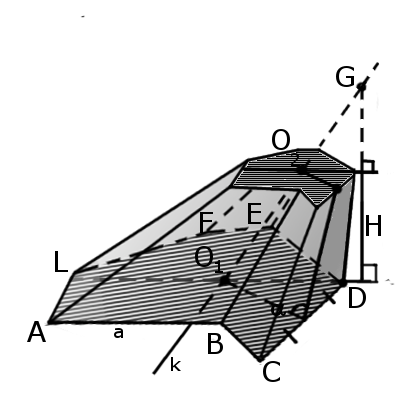
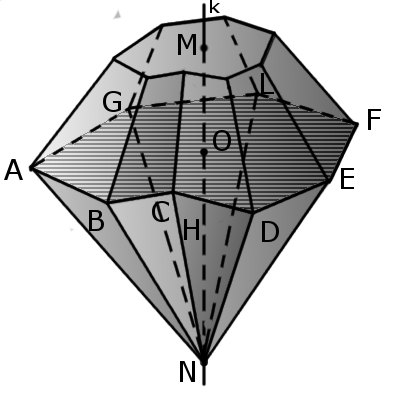
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
Как найти сторону основания пирамиды
Задачи на вычисление стороны основания пирамиды составляют в задачнике по геометрии довольно большой раздел. Очень многое зависит от того, какая гемоетрическая фигура лежит в основании, а также от того, что дано в условиях задачи.

Вам понадобится
- — чертежные принадлежности;
- — тетрадь в клетку;
- — теорема синусов;
- — теорема Пифагора;
- — калькулятор.
Инструкция
В школьном курсе геометрии рассматриваются главным образом пирамиды, в основании которых лежит правильный многоугольник, то есть такой, у которого все стороны равны. Проекция вершины пирамиды совпадает с центром ее основания. Начертите пирамиду, в основании которой лежит равносторонний треугольник. В условиях могут быть даны:
— длина бокового ребра пирамиды и угол его с ребром между боковой гранью и основанием;
— длина бокового ребра и высота боковой грани;
— длина бокового ребра и высота пирамиды.
Если известны боковое ребро и угол, задача решается несколько иначе. Вспомните, что собой представляет каждая боковая грань пирамиды, в основании которой лежит равносторонний многоугольник. Это равнобедренный треугольник. Проведите его высоту, которая одновременно является биссектрисой и медианой. То есть половина стороны основания a/2=L*cosA, где а – сторона основания пирамиды, L – длина ребра. Чтобы найти размер стороны основания, достаточно полученный результат умножить на 2.
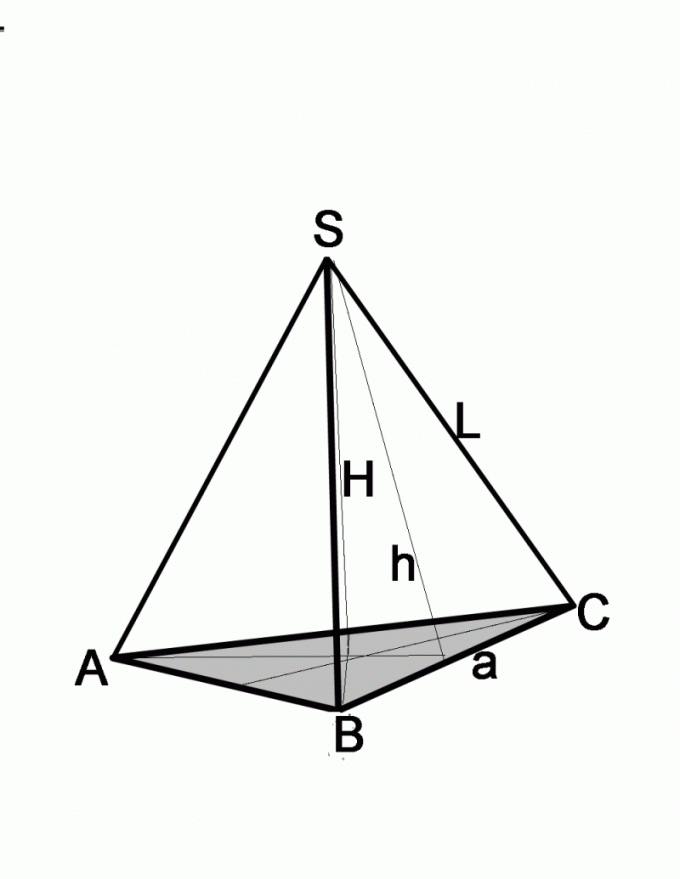
Если в задаче даны высота боковой грани и длина ребра, найдите сторону основания по теореме Пифагора. Боковая грань в данном случае будет гипотенузой, известная высота –з одним из катетов. Чтобы найти длину второго катета, нужно из квадрата гипотенузы вычесть квадрат второго катета, то есть (a/2)2=L2-h2, где а – сторона основания, L – длина боковой грани, h – высота боковой грани.
В этом случае нужно выполнить дополнительное построение, чтобы можно было оперировать тригонометрическими функциями. Вам даны боковое ребро L и высота пирамиды H, которая соединяет вершину пирамиды с центром основания. Из точки пересечения высоты с плоскостью основания проведите отрезок, соединив эту точку с одним из углов основания. У вас получился прямоугольный треугольник, гипотенузой которого является боковое ребро, одним из катетов – высота пирамиды. По этим данным легко найти второй катет треугольника, для этого достаточно из квадрата бокового ребра L вычесть квадрат высоты H. Дальнейшие действия зависят от того, какая именно фигура лежит в основании.
Вспомните свойства равностороннего треугольника. У него высоты одновременно являются биссектрисами и медианами. В точке пересечения они делятся пополам. То есть получается, что вы нашли половину высоты основания. Для удобства вычислений проведите все три высоты. Вы увидите, что отрезок, квадрат длины которого вы уже нашли, является гипотенузой прямоугольного треугольника. Извлеките квадратный корень. Вам известен и острый угол – 30°, так что найти половину стороны основания не составит особого труда, применив теорему косинусов.
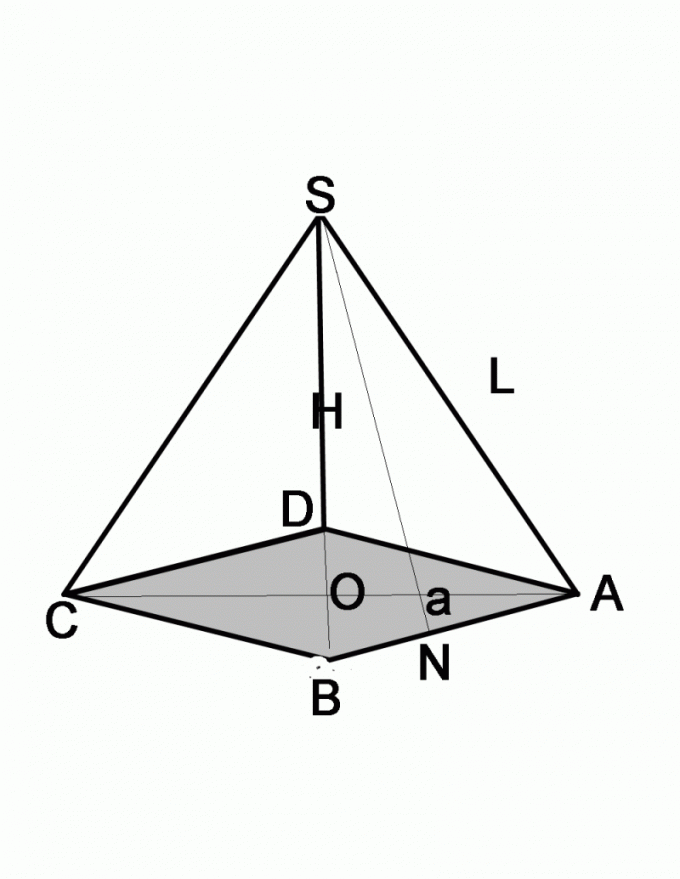
Для пирамиды, в основании которой лежит правильный четырехугольник, алгоритм будет тем же самым. Если вы вычтите из квадрата бокового ребра квадрат высоты пирамиды, получите возведенную в квадрат половину диагонали основания. Извлеките корень, найдите размер диагонали, которая одновременно является гипотенузой равнобедренного прямоугольного треугольника. Размер любого из катетов найдите по теореме Пифагора, синусов или косинусов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.