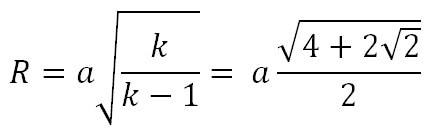Как найти сторону восьмиугольника описанного около окружности

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

• Расчет длины стороны
  • Через радиус вписанной окружности

  • Через радиус описанной окружности

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Через радиус вписанной окружности

Формула расчета

Через радиус описанной окружности

Формула расчета

Длина стороны правильного многоугольника

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Восьмиугольник описанный около окружности свойства

Правильный восьмиугольник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2021; проверки требует 1 правка.

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли [1] и может быть построен также как квазиправильный усечённый квадрат, t , в котором перемежаются два типа граней. Усечённый восьмиугольник (t ) является шестнадцатиугольником (t ).

Свойства[править | править код]

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет

Формулы расчёта параметров правильного восьмиугольника[править | править код]

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная ≈ 2.414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

• Радиус описанной окружности правильного восьмиугольника:

• Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Площадь через квадрат[править | править код]

Площадь можно также вычислить как усечение квадрата

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A (ширину восьмиугольника)

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Два катета углового треугольника можно получить по формуле

Симметрия[править | править код]

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih8 порядка 16. Имеется 3 диэдральные подгруппы — Dih4, Dih2 и Dih2, а также 4 циклические подгруппы — Z8, Z4, Z2 и Z1. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта [3].

Применение восьмиугольников[править | править код]

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

Зонты часто имеют восьмиугольную форму

Знаменитая восьмиугольная чашка с острова Белитунг

Производные фигуры[править | править код]

Связанные многогранники[править | править код]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

См. также[править | править код]

• Восьмерик
• Восьмиугольное число
• Октаграмма
• Площадь Октогон в Будапеште, Венгрия
• Сглаженный восьмиугольник

Примечания[править | править код]

Литература[править | править код]

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.

Восьмиугольник, виды, свойства и формулы

Восьмиугольник, виды, свойства и формулы.

Восьмиугольник — это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник, выпуклый и невыпуклый восьмиугольник

Правильный восьмиугольник (понятие и определение)

Свойства правильного восьмиугольника

Формулы правильного восьмиугольника

Правильный восьмиугольник в природе, технике и культуре

Восьмиугольник, выпуклый и невыпуклый восьмиугольник:

Восьмиугольник — это многоугольник с восемью углами.

Восьмиугольник — это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый восьмиугольник — это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник

Рис. 2. Невыпуклый восьмиугольник

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) — это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник — это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Свойства правильного восьмиугольника:

1. Все стороны правильного восьмиугольника равны между собой.

a1 = a2 = a3 = a4= a5 = a6 = a7 = a8.

2. Все углы равны между собой и составляют 135°.

α1 = α2 = α3 = α4 = α5 = α6 = α7 = α8 = 135°.

Рис. 4. Правильный восьмиугольник

3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник

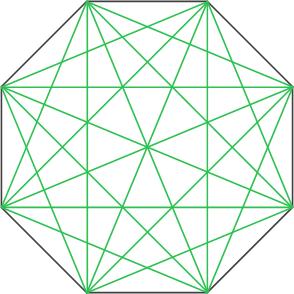
5. Количество диагоналей правильного восьмиугольника равно 20.

Рис. 6. Правильный восьмиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный восьмиугольник

Формулы правильного восьмиугольника:

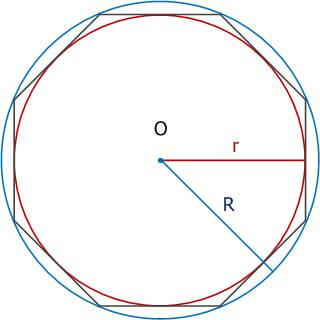
Пусть a — сторона восьмиугольника, r — радиус окружности, вписанной в восьмиугольник, R — радиус описанной окружности восьмиугольника, k — константа восьмиугольника, P — периметр восьмиугольника, S — площадь восьмиугольника.

Формула константы правильного восьмиугольника:

Формула периметра правильного восьмиугольника:

Формулы площади правильного восьмиугольника:

Формулы радиуса окружности, вписанной в правильный восьмиугольник:

Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:

Формулы стороны правильного восьмиугольника:

Правильный восьмиугольник в природе, технике и культуре:

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.

Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности 3 396

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли [1] и может быть построен также как квазиправильный усечённый квадрат, t , в котором перемежаются два типа граней. Усечённый восьмиугольник (t ) является шестнадцатиугольником (t ).

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет

Формулы расчёта параметров правильного восьмиугольника

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

• Радиус описанной окружности правильного восьмиугольника:

• Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Площадь через квадрат

Площадь можно также вычислить как усечение квадрата

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A (ширину восьмиугольника)

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Два катета углового треугольника можно получить по формуле

Симметрия

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih8 порядка 16. Имеется 3 диэдральные подгруппы — Dih4, Dih2 и Dih2, а также 4 циклические подгруппы — Z8, Z4, Z2 и Z1. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный?! восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта [3].

Применение восьмиугольников

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования

Зонты часто имеют восьмиугольную форму

Знаменитая восьмиугольная чашка с острова Белитунг

Производные фигуры

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

См. также

• Восьмерик
• Восьмиугольное число?!
• Октаграмма
• Площадь Октогон в Будапеште, Венгрия
• Сглаженный восьмиугольник?!

Примечания

Литература

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.

Многоугольники	[en] [de]
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники

Восьмиугольник — Octagon

В геометрии , восьмиугольник (от греческого ὀκτάγωνον oktágōnon , «восемь углов») представляет собой восьмигранный многоугольник или 8-угольник.

Регулярный восьмиугольник имеет символ шлефли , а также может быть выполнен в виде квазирегулярная усеченный квадрат , т , который чередуется два типа ребер. Усеченный восьмиугольник t представляет собой шестиугольник . Трехмерным аналогом восьмиугольника может быть ромбокубооктаэдр с треугольными гранями на нем, подобными замененным ребрам, если рассматривать восьмиугольник как усеченный квадрат.

Свойства общего восьмиугольника

Диагонали зеленого четырехугольника равны по длине и расположены под прямым углом друг к другу.

Сумма всех внутренних углов любого восьмиугольника составляет 1080 °. Как и у всех многоугольников, внешние углы составляют 360 °.

Если все квадраты построены изнутри или снаружи на сторонах восьмиугольника, то середины сегментов, соединяющих центры противоположных квадратов, образуют четырехугольник, который является как равдиагональным, так и ортодиагональным (то есть, диагонали которого равны по длине и расположены справа). углы друг к другу).

Середина восьмиугольник ссылочного восьмиугольника имеет свои восемь вершин на серединах сторон опорного восьмиугольника. Если все квадраты построены внутри или снаружи на сторонах восьмиугольника средней точки, то средние точки сегментов, соединяющих центры противоположных квадратов, сами образуют вершины квадрата.

Регулярный восьмиугольник закрытая фигура со сторонами одинаковой длины и внутренних углов одного и того же размера. Он имеет восемь линий отражательной симметрии и вращательной симметрии 8-го порядка. Правильный восьмиугольник представлен символом Шлефли . Внутренний угол в каждой вершине правильного восьмиугольника составляет 135 ° ( радиан ). Центральный угол равен 45 ° ( в радианах).

Область

Площадь правильного восьмиугольника со стороной а определяется выражением

С точки зрения радиуса описанной окружности R , площадь равна

В терминах апофемы r (см. Также вписанный рисунок ) площадь равна

Эти последние два коэффициента заключают в скобки значение пи , площадь единичного круга .

Площадь также можно выразить как

где S — размах восьмиугольника или второй по длине диагонали; и длина одной из сторон, или оснований. Это легко проверить, если взять восьмиугольник, нарисовать квадрат снаружи (убедившись, что четыре из восьми сторон перекрываются с четырьмя сторонами квадрата), а затем взять угловые треугольники (это 45-45-90 треугольников ). и размещает их так, чтобы прямые углы были направлены внутрь, образуя квадрат. Края этого квадрата равны длине основания.

Учитывая длину стороны a , промежуток S равен

Таким образом, пролет равен соотношению серебра, умноженному на сторону a.

Тогда область будет такой, как указано выше:

Выраженная в размахе, площадь равна

Еще одна простая формула для площади:

Чаще известен пролет S , а длина сторон a должна быть определена, как при разрезании квадратного куска материала на правильный восьмиугольник. Из вышеизложенного

Две конечные длины e с каждой стороны (длины сторон треугольников (зеленые на изображении), усеченные из квадрата), а также be могут быть рассчитаны как

Циркумрадиус и внутренний радиус

Описанной окружности регулярного восьмиугольника с точки зрения длиной стороны а является

и inradius является

(это половина отношения серебра, умноженная на сторону, a , или половину размаха, S )

Диагонали

С точки зрения длины стороны a правильный восьмиугольник имеет три различных типа диагоналей :

• Короткая диагональ;
• Средняя диагональ (также называемая размахом или высотой), которая в два раза превышает длину внутреннего радиуса;
• Длинная диагональ, которая в два раза превышает длину описанной окружности.

Формула для каждого из них следует из основных принципов геометрии. Вот формулы для их длины:

Конструкция и элементарные свойства

построить правильный восьмиугольник, сложив лист бумаги

Правильный восьмиугольник в данной описанной окружности может быть построен следующим образом:

1. Нарисуйте круг и диаметр AOE, где O — центр, а A, E — точки на описанной окружности.
2. Нарисуйте ГОК другого диаметра, перпендикулярно AOE.
3. (Попутно заметим, что A, C, E, G — вершины квадрата).
4. Нарисуйте биссектрисы прямых углов GOA и EOG, образуя еще два диаметра HOD и FOB.
5. A, B, C, D, E, F, G, H — вершины восьмиугольника.

Октагон в данном описанном круге

Правильный восьмиугольник можно построить с помощью линейки и циркуля , так как 8 = 2 3 , степень двойки :

Конструкция восьмиугольника Meccano.

Правильный восьмиугольник можно сконструировать из металлических брусьев. Требуется двенадцать стержней размера 4, три стержня размера 5 и два стержня размера 6.

Каждая сторона правильного восьмиугольника образует половину прямого угла в центре круга, соединяющего его вершины. Таким образом, его площадь можно вычислить как сумму 8 равнобедренных треугольников, что приведет к результату:

для восьмиугольника стороны а .

Стандартные координаты

Координаты вершин правильного восьмиугольника с центром в начале координат и длиной стороны 2:

Расслоение

Кокстеровские гласит , что каждый зоногон (2 м -угольник которого противоположные стороны параллельны и равны по длине) можно разрезать на м ( м -1) / 2 параллелограммов. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильного восьмиугольника , м = 4, и она может быть разделена на 6 ромбов, с одним примером , показанным ниже. Это разложение можно увидеть как 6 из 24 граней в плоскости проекции многоугольника Петри тессеракта . Список (последовательность A006245 в OEIS ) определяет количество решений как 8 по 8 ориентациям этого одного разреза. Эти квадраты и ромбы используются в мозаиках Амманна — Бенкера .

Наклонный восьмиугольник

Правильный скошенный восьмиугольник, видимый как края квадратной антипризмы , симметрия D 4d , [2 + , 8], (2 * 4), порядок 16.

Перекос восьмиугольника является перекос многоугольник с 8 вершинами и ребрами , но не существующие на одной и той же плоскости. Внутренний вид такого восьмиугольника обычно не определяется. У косого зигзагообразного восьмиугольника вершины чередуются между двумя параллельными плоскостями.

Регулярная перекос восьмиугольника является вершиной-симметрический с равными длинами ребер. В 3-х измерениях это будет зигзагообразный скошенный восьмиугольник, который можно увидеть в вершинах и боковых гранях квадратной антипризмы с той же симметрией D 4d , [2 + , 8], порядка 16.

Полигоны Петри

Правильный косой восьмиугольник — это многоугольник Петри для этих многомерных регулярных и однородных многогранников , показанных в этих косых ортогональных проекциях на плоскости Кокстера A 7 , B 4 и D 5 .

Симметрия восьмиугольника

Многоугольники	[en] [en] [en] [de] [de]
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники

11 симметрий правильного восьмиугольника. Линии отражений синие по вершинам, пурпурные по краям, а порядок вращения указан в центре. Вершины окрашены в соответствии с их положением симметрии.

Правильный восьмиугольник имеет DIH 8 симметрии, порядка 16. Есть 3 двугранные подгруппы: DIH 4 , DIH 2 и DIH 1 , и 4 — циклические подгруппы : Z 8 , Z 4 , Z 2 и Z 1 , последние не подразумевает никакой симметрии .

На правильном восьмиугольнике есть 11 различных симметрий. Джон Конвей обозначает полную симметрию как r16 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g для их центральных порядков вращения. Полная симметрия регулярной формы равна r16, а симметрия не помечена как a1 .

Наиболее распространенными восьмиугольниками с высокой симметрией являются p8 , изогональный восьмиугольник, построенный из четырех зеркал, может чередоваться длинные и короткие края, и d8 , изотоксальный восьмиугольник, построенный с равной длиной ребер, но вершинами, чередующимися с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного восьмиугольника.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но ее можно рассматривать как направленные грани .

Использование восьмиугольников

План восьмиугольного этажа Купола Скалы.

Восьмиугольная форма используется как элемент дизайна в архитектуре. Купол Скалы имеет характерный восьмиугольный план. Башня ветров в Афинах является еще одним примером восьмиугольной структуры. Восьмиугольный план также использовался в церковной архитектуре, такой как собор Святого Георгия, Аддис-Абеба , базилика Сан-Витале (в Равенне, Италия), Кастель-дель-Монте (Апулия, Италия), баптистерий Флоренции , церковь Цум-Фридефюрстен (Германия) и количество восьмиугольных церквей в Норвегии . Центральное пространство Ахенского собора , Палатинская капелла Каролингов , имеет правильную восьмиугольную планировку. Использование восьмиугольника в церквах также включает в себя меньшие элементы дизайна, такие как восьмигранная апсида из Nidaros собора .

Такие архитекторы, как Джон Эндрюс , использовали восьмиугольную планировку этажей в зданиях для функционального отделения офисных помещений от строительных услуг, в частности, штаб-квартиру Intelsat в Вашингтоне, округ Колумбия, офисы Callam в Канберре и офисы Octagon в Парраматте , Австралия.

Другое использование

Зонты часто имеют восьмиугольный контур.

В знаменитом ковре «Бухара » использован мотив восьмиугольной «слоновьей ноги».

Улица и блок макет Барселона «s Эшампль района базируются на нерегулярных восьмиугольниках

Чанги использует восьмиугольные фигуры.

Японские лотереи часто имеют восьмиугольную форму.

Значок знака остановки с рукой посередине.

Занятия в Shimer College традиционно проходят за восьмиугольными столами.

Производные цифры

Восьмиугольника , как усеченная площадь , является первым в последовательности усеченных гиперкуб :

Изображение	…
Имя	Восьмиугольник	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Усеченный 7-куб	Усеченный 8-куб
Диаграмма Кокстера
Фигура вершины	() v ()	() v	() v	() v

Как расширенный квадрат, он также является первым в последовательности расширенных гиперкубов:

Правильный многоугольник

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Восьмиугольник, виды, свойства и формулы

Формулы расчёта параметров правильного восьмиугольника

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная (1+2) >)> ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

Радиус описанной окружности правильного восьмиугольника:

Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Литература

• Pierre Wantzel. Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas // Journal de Mathématiques. — 1837. — С. 366–372.
• W. W. Rose Ball, H. S. M.Coxeter. Mathematical recreations and Essays. — Thirteenth edition. — New York: The MacMillan company, 1947. — С. 141.

Перевод: Математические эссе и развлечения / перевод Н.И. Плужниковой, А.С.Попова, Г.М. Цукерман, под редакцией И.М.Яглома. — Москва: «Мир», 1986. — С. 156.

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Chaim Goodman-Strauss, 2008. — С. 275—278. — ISBN 978-1-56881-220-5.

Branko Grünbaum. Metamorphoses of polygons // The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History. — 1994.

Jay Bonner. Islamic geometric pattens. — Springer, 2017. — ISBN 978-1-4419-0216-0.

Nielsen D. Design & Nature V: Comparing Design in Nature with Science and Engineering // Fifth international conference on comapring design in nature with science engineering / Angelo Carpi, C. A. Brebbia. — WIT Press, 2010. — ISBN 978-1-84564-454-3.

Вёрман К. История искусств всех времен и народов. — Москва, Берлин: Директ-медиа, 2015. — Т. 3 Книга2-3. — ISBN 978-5-4475-3827-9.

Применение восьмиугольников

Дорожный знак «Движение без остановки запрещено»

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и . Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Построение

Точное построение

Проводим большую окружность k₁ (будущую описанную окружность семнадцатиугольника) с центром O.
Проводим её диаметр AB.
Строим к нему перпендикуляр m, пересекающий k₁ в точках C и D.
Отмечаем точку E — середину DO.
Посередине EO отмечаем точку F и проводим отрезок FA.
Строим биссектрису w₁ угла ∠OFA.
Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
Проводим s — перпендикуляр к w₂ из точки F.
Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
Строим окружность Фалеса (k₂) на диаметре HA. Она пересекается с CD в точках J и K.
Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N

Здесь важно не перепутать N с M, они расположены очень близко.
Строим касательную к k₃ через N.

Точки пересечения этой касательной с исходной окружностью k₁ — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.

Примерное построение

Следующее построение хоть и приблизительно, но гораздо более удобно.

1. Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
2. Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
3. Делим пополам отрезок EB (точка F).
4. строим перпендикуляр к AB в точке F.

Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.

Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P₃ и P₁₄.

При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.
Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.
Углы равны по 108 градусов.
Центры вписанной и описанной окружностей совпадают.
Сумма внутренних углов равна 180 * (5 – 2) = 540 (градусов), а внешних – 360.
Количество диагоналей соответствует 5.
Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
Биссектрисы, проведенные через центр, равны.
Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Другие восемнадцатиугольники фигуры

Звёздчатые 18 -угольники имеют символы >. Существует два правильных звёздчатых многоугольника: 185 > и >. Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: > эквивалентен 2 > (двум девятиугольникам), > эквивалентен 3 > (трём шестиугольникам), > и > эквивалентны 2 > и 2 > (двум эннеаграммам), > эквивалентен 6 > (6 равносторонним треугольникам), и, наконец, > эквивалентен 9 > (девять двуугольников).

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?

Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла. Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.

Правильный многоугольник

• формулы, признаки и свойства правильного многоугольника
• формулы правильного n-угольника
• правильный треугольник
• правильный четырехугольник
• правильный шестиугольник
• правильный восьмиугольник