Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.
- Сторона треугольника равностороннего через радиус описанной
окружности - Сторона треугольника равностороннего через радиус вписанной
окружности - Сторона треугольника равностороннего через высоту
- Сторона треугольника равностороннего через площадь
треугольника - Основание равнобедренного треугольника через боковые
стороны и угол между ними - Основание равнобедренного треугольника через боковые
стороны и угол при основании - Боковая сторона равнобедренного треугольника через
основание и угол между боковыми сторонами - Боковая сторона равнобедренного треугольника через
основание и угол при основании - Катет прямоугольного треугольника через гипотенузу и острый
угол - Катет прямоугольного треугольника через гипотенузу и другой
известный катет - Гипотенуза прямоугольного треугольника через катет и острый
угол - Гипотенуза прямоугольного треугольника через катеты
- Сторона треугольника через две известные стороны и угол
между ними - Сторона треугольника через известную сторону и два угла
Сторона равностороннего треугольника через радиус описанной окружности
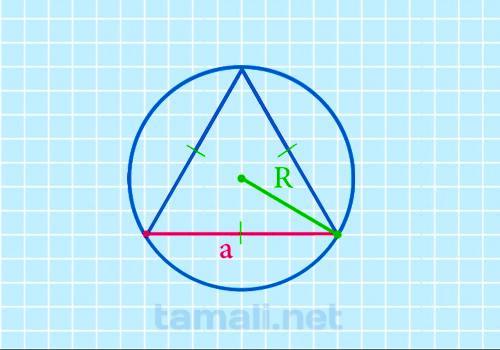
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:
a = R * √3
где а — сторона треугольника, R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.
Сторона равностороннего треугольника через радиус вписанной окружности
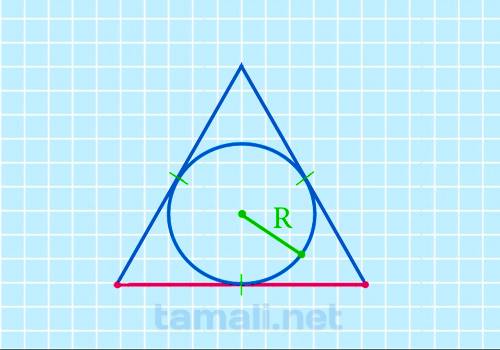
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):
a = 2r * √3
где а — сторона треугольника, R — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.
Сторона равностороннего треугольника через высоту
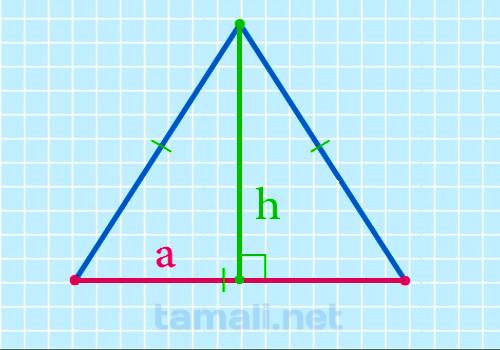
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:
a = 2h / √3
где а — сторона, h — высота равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.
Сторона равностороннего треугольника через площадь
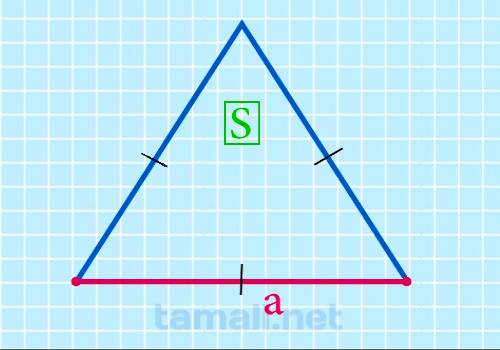
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу
a = √(4S / √3)
где а — сторона, S — площадь равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.
Основание равнобедренного треугольника через боковые стороны и угол между ними
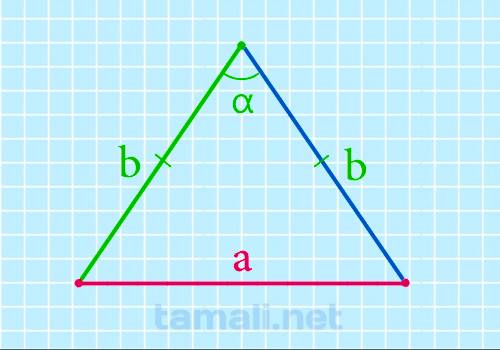
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:
a = 2b * sin (α/2)
где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.
Основание равнобедренного треугольника через боковые стороны и угол при основании
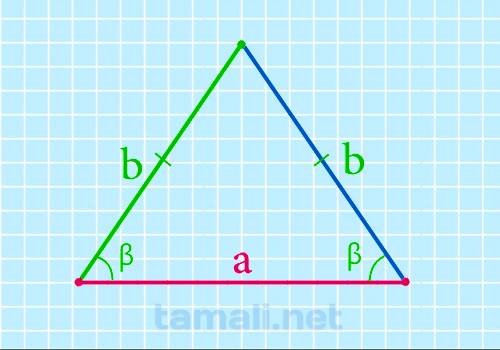
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:
a = 2b + cos β
где b — боковая сторона, β — угол при основании.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.
Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
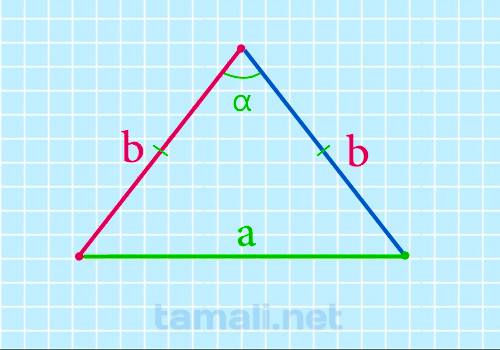
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным. Это значит, что α = β.
Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:
b = a / (2 * sin(α/2))
где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.
Боковая сторона равнобедренного треугольника через основание и угол при основании
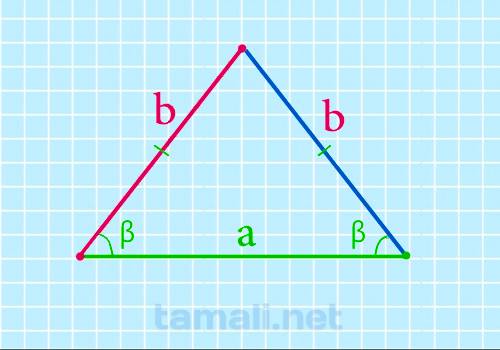
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:
b = a / 2 * cos β
где a — это основание, β — угол при основании равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.
Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.
Катет прямоугольного треугольника через гипотенузу и острый угол
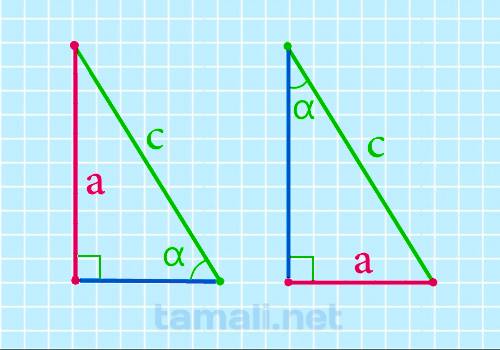
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:
a = c * sin α
где c — гипотенуза, α — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее: a = 77 * 0,98 = 75,8см.
Катет прямоугольного треугольника через гипотенузу и другой известный катет
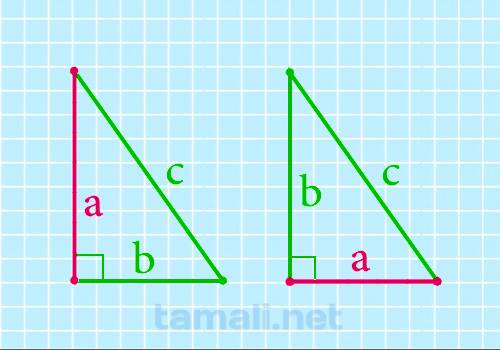
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:
a = √(c² — b²)
где c — гипотенуза, b — катет который известен прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см
Гипотенуза прямоугольного треугольника через катет и острый угол
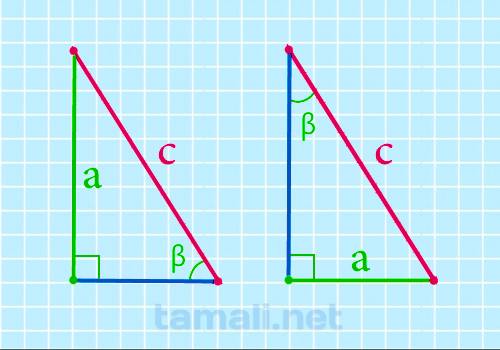
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:
c = a / sin(β)
где a — катет, β — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.
Гипотенуза прямоугольного треугольника через катеты
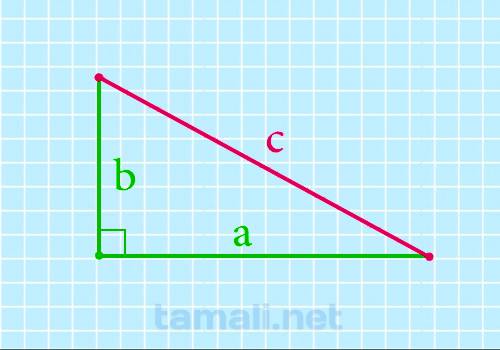
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:
c = √(a² + b²)
где c — гипотенуза, a и b — катеты.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см
Сторона треугольника через две известные стороны и угол между ними
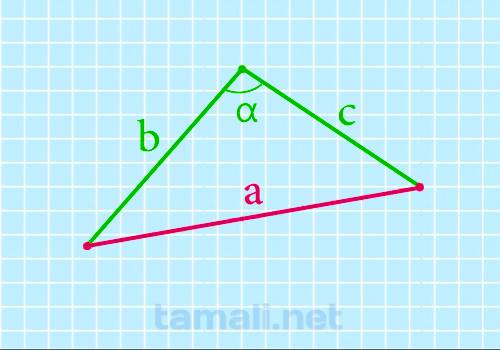
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:
a = b² + c² — 2bc * cos α
где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.
Цифр после
запятой:
Результат в:
Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.
Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.
Сторона треугольника через известную сторону и два угла
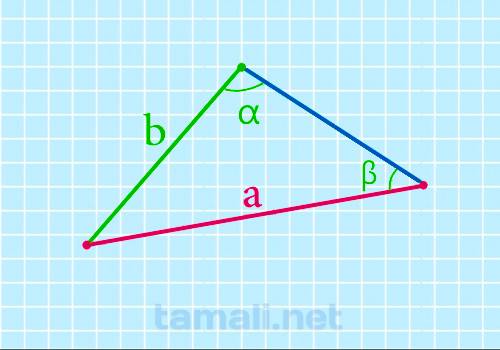
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:
a = (b * sin α) / sin β
где b — сторона треугольника; β, α — углы треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть сторона треугольника b равна 10, угол β = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30 = 8.71723 мм.
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b — катеты, с — гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b — катеты, с — гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a — искомая сторона, S — площадь треугольника.
2) Найти сторону через высоту
где a — искомая сторона,h — высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a — искомая сторона,r — радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a — искомая сторона,R — радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a — искомая сторона, b — известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
как найти стороны треугольника если дан радиус описанной окружности
Отношение сторон треугольника к синусам противолежащих углов равны и равны диаметру описанной окружности. Отсюда любая сторона треугольника равна удвоенному радиусу описанной окружности, умноженному на синус противолежащего угла. Третий угол треугольника найти элементарно, зная два других, из теоремы о сумме углов треугольника.
P.S.
Блин, обязательно кто-нибудь опередит.. .
Теорему синусов в школе проходят, но о последнем равенстве в большинстве случаев почему-то умалчивается.
Есть такая теорема, которая называется теорема синусов.
Али в школе не проходили?
И теорему о сумме углов в треугольнике тоже не проходили, походу?
Радиус описанной окружности равностороннего треугольника
Зная радиус описанной окружности, можно найти сразу не только сторону равностороннего треугольника, но и радиус вписанной в него окружности, так как они напрямую связаны друг с другом. Сторона треугольника будет равна произведению радиуса описанной окружности на корень из трех, а радиус вписанной окружности – его половине. (рис.100) a=√3 R r=R/2
Чтобы вычислить периметр и площадь равностороннего треугольника через радиус описанной вокруг него окружности, необходимо подставить полученное выражение для стороны в соответствующие формулы. P=3a=3√3 R S=(√3 a^2)/4=(3√3 R^2)/4
Высоты, медианы и биссектрисы являются одними и теми же отрезками в равностороннем треугольнике, и вычислить их можно по единой формуле, где искомая величина равна корню из трех, умноженному на сторону и деленному на два. Подставив вместо стороны произведение радиуса и корня из трех, получаем, что высота равна трем радиусам, деленным на два. (рис.99) h=m=l=(√3 a)/2=(√3 √3 R)/2=3R/2
Чтобы найти среднюю линию равностороннего треугольника через радиус описанной вокруг него окружности, необходимо разделить произведение радиуса и корня из трех на два. (рис.97.3) M=(√3 R)/2
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
- Расчет длины стороны
- Через радиус вписанной окружности
- Через радиус описанной окружности
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
-
Расчет длины стороны
- Через радиус вписанной окружности
- Через радиус описанной окружности
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Через радиус вписанной окружности
Формула расчета
Через радиус описанной окружности
Формула расчета
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
[ r = frac{S}{(a+b+c)/2} ]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
[ r = frac{S}{frac{1}{2}P} ]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
[ r = sqrt{frac{(p-a)(p-b)(p-c)}{p}} ]
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
[ R = frac{AC}{2 sin angle B} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
[ R = frac{abc}{4S} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:[ R = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}} ]
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:[ S = pr ]
- Площадь треугольника вписанного в окружность,
если известен полупериметр:[ S = sqrt{p(p-a)(p-b)(p-c)} ]
- Площадь треугольника вписанного в окружность,
если известен высота и основание:[ S = frac{1}2 ah ]
- Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:[ S = frac{a^2}{2cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} ]
- Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:[ S = frac{1}{2}ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
[ P = a + b + c ]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
[ P = frac{2S}{r} ]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:[ P = sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) ]
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:[ a = sqrt{b^2+c^2 -2bc cdot cos alpha} ]
- Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
[ a = frac{b · sin alpha }{sin β} ]
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
[ l = frac{AB}{2} ]
- Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:
[ l = frac{sqrt{b^2+c^2-2bc cdot cos alpha}}{2} ]
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:[ h = frac{2S}{a} ]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:[ h = b cdot sin alpha ]
- Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:[ h = frac{bc}{2R} ]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
Дано: окружность и треугольник,
которые изображены на рисунке 2.
Доказать: окружность описана
около треугольника.
Доказательство:
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
Следовательно: окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.



























