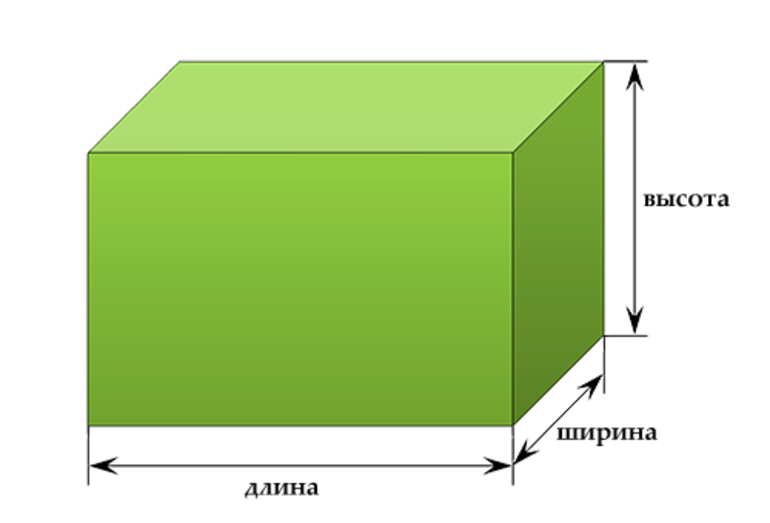
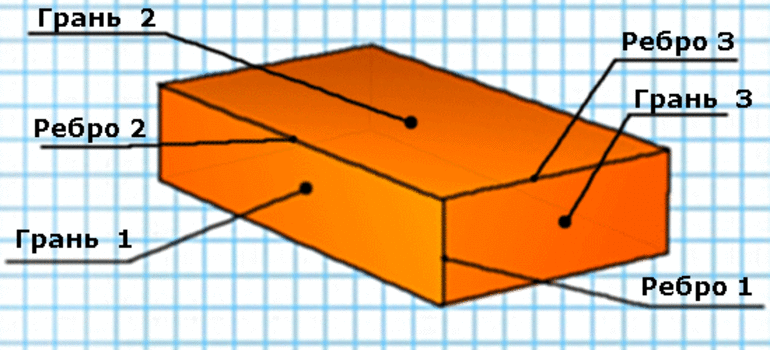
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
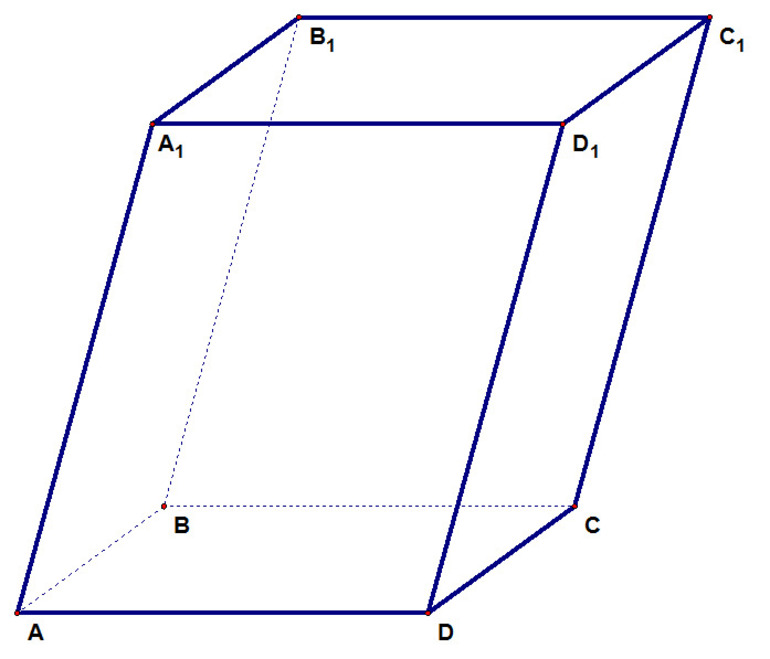
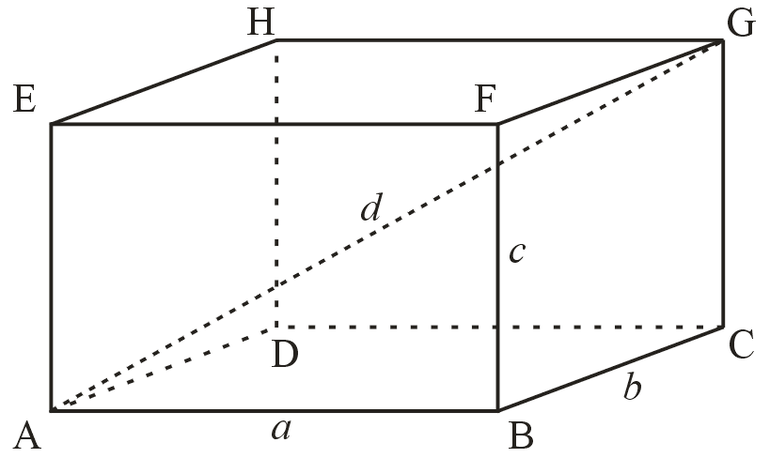
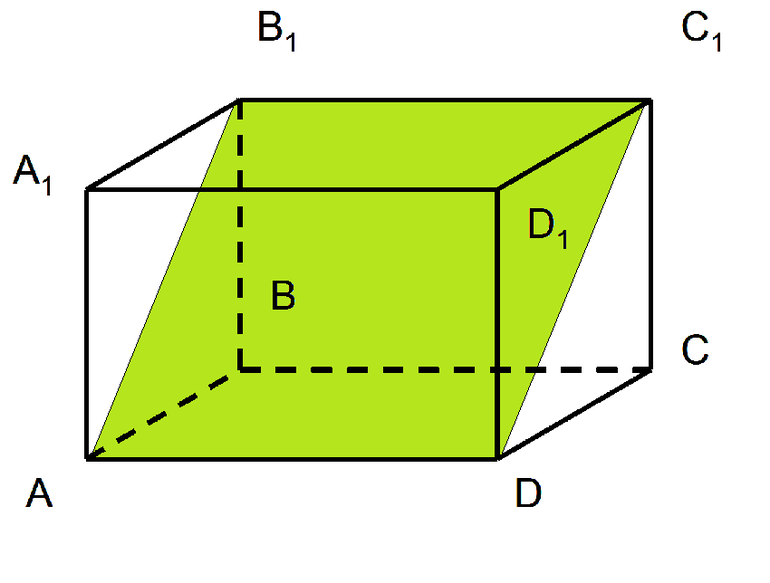
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса — бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
|
Как найти длину диагонали прямоугольного параллелепипеда ? По какой формуле найти диагональ параллелепипеда ?Диагональ прямоугольного параллелепипеда — это отрезок, соединяющий его противоположные вершины . Итак, у нас есть прямоугольный параллелепипед с диагональю d и со сторонами a, b, c . Одно из свойств параллелепипеда гласит, что квадрат длины диагонали d равен сумме квадратов трёх его измерений a, b, c. Отсюда вывод, что длина диагонали может быть легко рассчитана по следующей формуле : Также :Как найти высоту параллелепипеда?модератор выбрал этот ответ лучшим Nonsense 7 лет назад Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле: где
Можно дать и другое определение, рассматривая декартову прямоугольную систему координат: Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси. Проекции совпадают с вершинами данного параллелепипеда. Zolotynka 8 лет назад Если у прямоугольного параллелепипеда известны длина, высота и ширина (a,b,c) то формула для расчета диагонали будет выглядеть таким образом: Обычно учителя не предлагают своим ученикам «голую» формулу, а прилагают усилия, чтобы те могли самостоятельно ее вывести, задавая наводящие вопросы:
Обычно после ответа на поставленные вопросы, ученики без труда самостоятельно выводят данную формулу. Лолочка611 8 лет назад Прямоугольный параллелепипед это один из так званных многогранников, который состоит из 6 граней, каждая из которых является прямоугольником. А диагональ — это отрезок, который соединяет противоположные вершины параллелограмма. Если длину, ширину и высоту прямоугольного параллелепипеда принять за a, b, c соответственно, то формула его диагонали ( D ) будет выглядеть следующим образом: D^2=a^2+b^2+c^2. дольфаника 8 лет назад Нашлась в интернете неплохая схема-таблица с полным перечислением всего, что есть в параллепипеде. Есть формула, чтобы найти диагональ, которая обозначается d. Есть изображение грани, вершины и других важных для параллепипеде вещей. Багира999 8 лет назад Прямоугольный параллелепипед — это разновидность многогранника, состоящая из 6 граней, в основании которого — прямоугольник. Диагональ — это отрезок, который соединяет противоположные вершины параллелограмма. Формула нахождения длины диагонали — квадрат диагонали равен сумме квадратов трех измерений параллелограмма. Koluchiy 8 лет назад Диагонали прямоугольного параллелепипеда равны. Также как и диагонали его противоположных граней. Длину диагонали можно вычислить, зная длину рёбер параллелограмма, исходящих из одной вершины. Эта длина равна корню квадратному из суммы квадратов длин его рёбер. ДРЕССИРОВЩИК 9 лет назад Квадрат диагонали, квадратного параллилепипеда (смотрите свойства квадратного параллепипеда) равна сумме квадратов трёх его разных сторон (ширине, высоте, толщине), а соответственно диагонали квадратного параллепипеда равна корню из этой суммы. haleron 8 лет назад Насколько мне известно еще со школьной программы, класс 9 если не ошибаюсь, и если не изменяет память , то диагональ прямоугольного параллелепипеда ровна корню квадратному суммы квадратов его всех трех сторон. [пользователь заблокирован] 8 лет назад квадрат диагонали равен, сумме квадратов ширины , высоты и длинны , исходя с этой формулы получаем ответ , диагональ равно корню квадратному с суммы его трех разных измерений , буквами они позначаюnсz abc Космос111 7 лет назад Вспоминаю школьную программу по геометрии, можно сказать так: диагональ параллелепипеда равняется корню квадратному полученному из суммы его всех трех сторон (обозначаются они маленькими буквами a, b, c). Николай Л 10 лет назад Длина диагонали прямоугольного параллепипеда равна корню квадратному из суммы квадратов его сторон. Знаете ответ? |
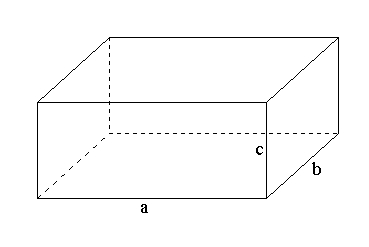
Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.
Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в формулах параллелепипеда при вычислении объема и площади.
Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.
Формула диагонали параллелепипеда
Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:
d2 = a2 + b2 + c2
Формула площади параллелепипеда
Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:
S = 2(ab + ac + bc)
Формула объема параллелепипеда
Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:
V = abc
Общая характеристика
В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.
Основные понятия и классификация
Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:
- Прямой. Четыре боковые грани имеют углы по 90 градусов.
- Прямоугольный. Каждая сторона фигуры является прямоугольной.
- Наклонный.
- Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
- Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
- Ромбоэдр. Стороны являются одинаковыми ромбами.
- Куб. Параллелепипед с равными (квадратными) сторонами.
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.
Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.
При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:
- любые стороны являются параллелограммами (с симметрией);
- стороны, расположенные друг против друга, будут параллельными и равными.
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.
Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2
Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.
Формулы и анализ
Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:
- V=a*b*c.
- S б =2*c*(a+b).
- S п =2*(a*b+b*c+a*c).
Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.
Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.
Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.
Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.
∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.
∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.
Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.
S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:
- Sбок — площадь параллелепипеда;
- Р — периметр;
- h — высота, перпендикулярная основанию.
Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.
Практическое применение
Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.
Доказательство теорем
Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).
Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.
Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.
Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.
Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.
Решение задач
Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.
Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.
Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.
Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).
Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.
Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.
Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:
- 78 = корень из суммы 5508+с2
- 782 = 5508 + с2
- с2 = 6084 — 5508.
- С2 = 576.
Ответ: объем составляет 576.
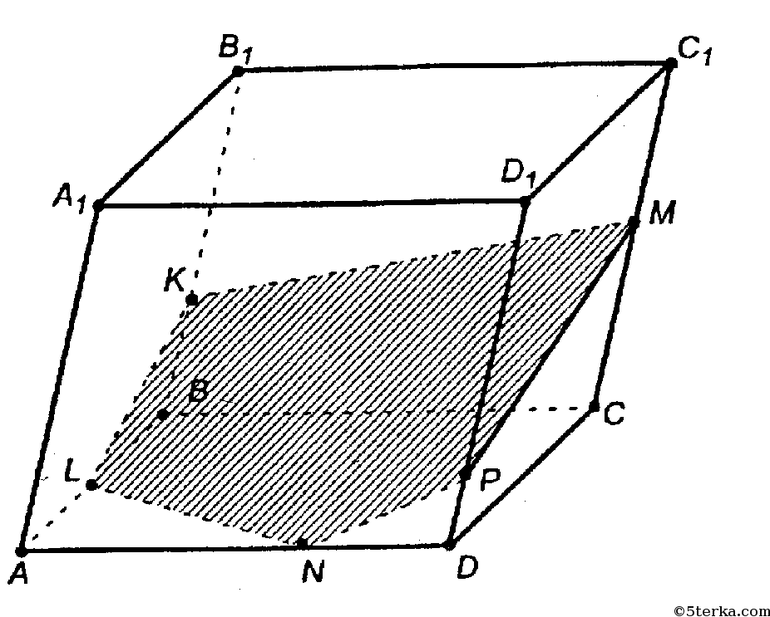
Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.
KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².
Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.
В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.
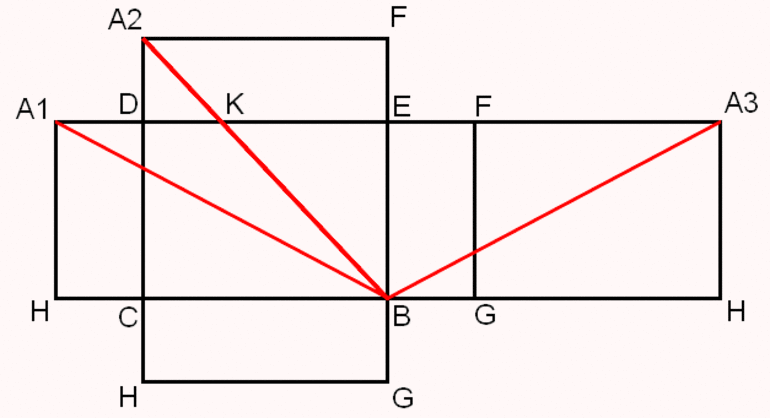
Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.
Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.
В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.
Высота треугольника делит его основание пополам. По теореме Пифагора она равна:
- FK2 + (AC/2)2 = FC2;
- FK2 + 16 = 25;
- FK2 =25−16 = 9;
- FK = 3 см.
Высота фигуры составляет 3 см.
Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.
Геометрия,
вопрос задал lanayoshida46,
4 года назад
lanayoshida46:
А если известно, что диагональ параллелепипеда наклонена к плоскости основания под углом 60°?
zmeura1204:
Вот так можно.
zmeura1204:
А какие именно вам даны величины. Это важно. Высота, или в основании?
lanayoshida46:
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
8 см и 10 см. Диагональ параллелепипеда наклонена к плоскости основания под углом 600
.
Найдите объем параллелепипеда.
zmeura1204:
Например если это основание. Тогда по Теореме Пифагора найти диагональ прямоугольника √(10²+8²)=√164=2√41.
zmeura1204:
А теперь tg60=h/2√41
zmeura1204:
Условие у вас не очень правильное, таким методом можно иметь три решения.
lanayoshida46:
мне хотя бы одно решение, вообще геометрию не понимаю
lanayoshida46:
помогите пожалуйста
Ответы на вопрос
Ответил ranohonhasimova
0
Ответ:
(8+10)×2 так найти параллелепипеда
Решение:
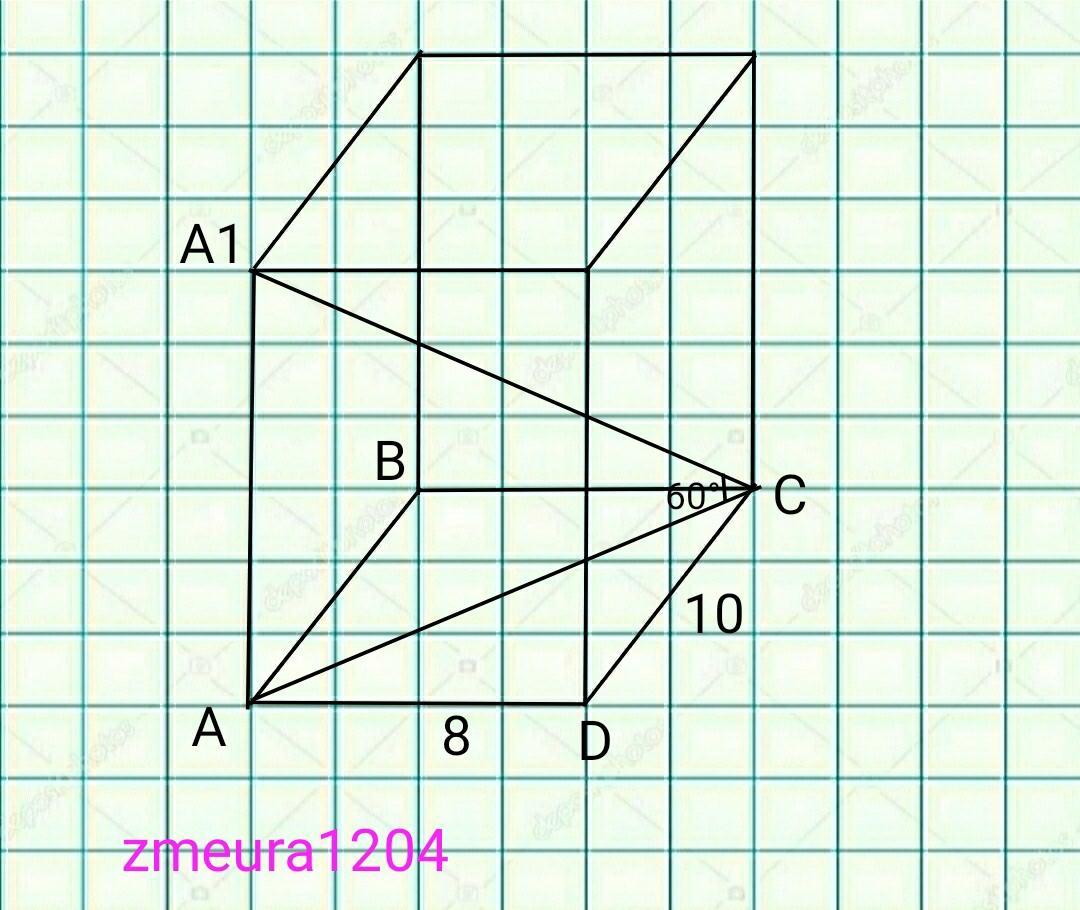
∆АDC- прямоугольный треугольник
По теореме Пифагора
АС=√(АD²+DC²)=√(8²+10²)=
=√(64+100)=√164=2√41 см
tg∠A1CA=AA1/AC
tg60°=√3
√3=AA1/2√41
AA1=2√41*√3=2√123
V=AD*AB*AA1=8*10*2√123=160√123 см³.
Ответ: 160√123см³.
Приложения:
lanayoshida46:
спасибо :3
lanayoshida46:
можете посмотреть другие мои вопросы по геометрии? Если вам не сложно конечно
lanayoshida46:
можете помочь пожалуйста?
lanayoshida46:
если вам не сложно конечно
lanayoshida46:
я болела и не понимаю как их делать, даже видео уроки не помогают 
lanayoshida46:
я болела и не понимаю как их делать, даже видео уроки не помогают 
lanayoshida46:
я болела и не понимаю как их делать, даже видео уроки не помогают 
Новые вопросы