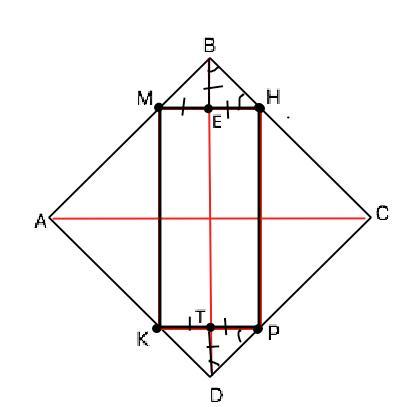
№ 45. В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12 м.
(диагонали квадрата пересекаются под прямым углом).
(как соответственные углы для параллельных прямых
и секущей АС). АС — биссектриса, поэтому
Значит,
равнобедренный; так как
является высотой, биссектрисой, а значит и медианой. Значит
равнобедренный, значит,
Так что,
Пусть отрезок
м, тогда
м и
Далее,
12;
Тогда
Ответ:
�������
� ������� ������ ������������� ���, ��� �� ������ �������
�������� ��������� ���� ������� �������������� � �������
�������������� ����������� ���������� ��������. ������� �������
����� ��������������, ����, ��� ���� �� ��� ����� ������ ������ �
��� ��������� �������� ����� 12.
���������
��������, ��� ��������� �������� ����� ������������� ��������������.
�������
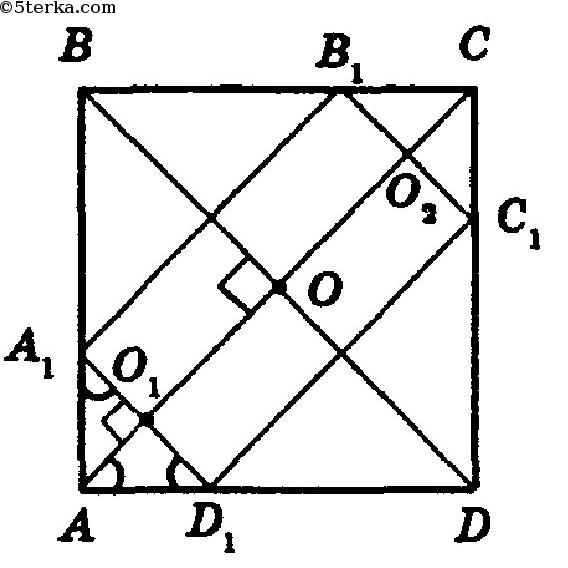
����� ������� M, N, K, L �������������� MNKL �����������
�������������� �� �������� AB, BC, CD, AD �������� ABCD;
MN = 2KL; ������� MN ����������� ��������� AC ��������; P �
Q — ����� ����������� AC � ���������������� ��������� ML � NK
�������������� MNKL. ���������
ML = NK = 2x,
MN = KL = 4x. �����
MP = NQ = x.
��������� APM � CQN — �������������� �������������
������������, ��
AP = MP = x �
CQ = NQ = x. �������
PM + MN + NQ = AP + PQ + QC = 12, ��� x + 4x + x = 12.
������ �������, ��� x = 2. �������������,
MN = 4x = 8, KN = 2x = 4.
�����
4 � 8.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 1284 |
В квадрат вписан прямоугольник так, что на каждой стороне квадрата лежит вершина прямоугольника, а его стороны параллельны диагоналям квадрата. Найти стороны прямоугольника, если одна из них на 6 см больше другой, а диагональ квадрата равна 30 см
Сделаем рисунок.
Треугольники ВМК, АКТ, МСН и НDT — равнобедренные прямоугольные.
ОА=АС:2=15 см
Пусть ВК=х
Тогда АК=АВ-х
По известному свойству гипотенузы равнобедренного прямоугольного треугольника
АВ=15√2
АК=15√2 -х
КМ=х√2
КТ=(15√2 -х )*√2=30-х√2
По условию КТ-КМ=6 см
30-х√2 -х√2=6
24=2х√2
х=24:2√2=12:√2
Умножим числитель и знаменатель на √2, чтобы избавиться от дроби:
х=12:√2=(12*√2):√2*√2х=6√2
КМ=6√2*√2=12 см
КТ=30-х√2=30-12=
18 см
КТ-КМ=18-12=6 см
[16.12.2013 19:29]
Решение 2327:
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника паралл
…
Подробнее смотрите ниже
Номер задачи на нашем сайте: 2327
ГДЗ из решебника:
Тема:
6. Четырехугольники
Нашли ошибку? Сообщите в комментариях (внизу страницы)
|
Раздел: Геометрия Полное условие: В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12 м.Решение, ответ задачи 2327 из ГДЗ и решебников: Этот учебный материал представлен 1 способом:
|
||
| Счетчики: 5520 | Добавил: Admin |
| Добавить комментарий
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
Ответ: 21 (ед. длины)
Объяснение: Поскольку стороны вписанного прямоугольника параллельны диагоналям квадрата, диагональ ВD квадрата делит периметр прямоугольника на две равные половины ТКМЕ и ТРНЕ. Как известно, диагонали квадрата делят его углы пополам. При этом угловые треугольники МВН и КDР – равные прямоугольные равнобедренные, в которых ВЕ=ЕМ=ЕН и TD=ТК=РТ. Заметим, что МК+МЕ+ТК=DВ=10,5 — это длина половины периметра прямоугольника. Полный периметр прямоугольника КМНР=2•10,5=21 ( ед. длины)
Приложения:













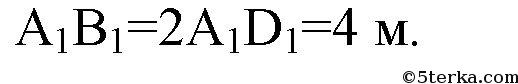







 Для просмотра в натуральную величину нажмите на картинку
Для просмотра в натуральную величину нажмите на картинку