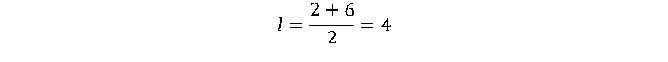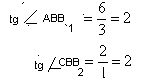Как найти стороны треугольника на клетчатой бумаге - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

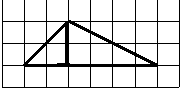
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Площадь прямоугольного треугольника будем искать с помощью формулы

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

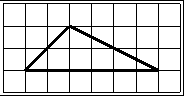
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

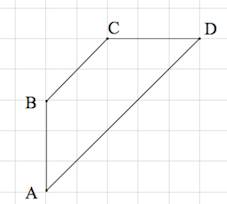
Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

Площади прямоугольных треугольников найдём по формуле

Как считать треугольник по клеткам

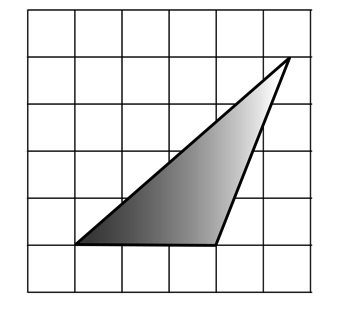
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому

см 2 .

Приведём другое решение:

Воспользуемся формулой для нахождения площади треугольника

Одна из сторон данного треугольника является диагональю квадрата со стороной 6, а высота, проведённая к этой стороне, является диагональю квадрата со стороной 2. Тогда

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

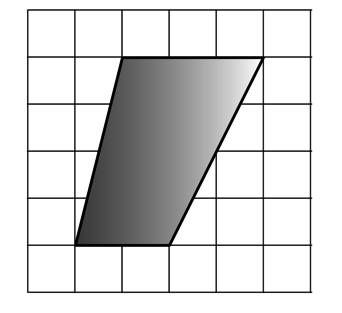
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

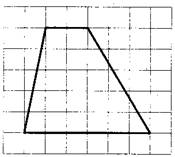
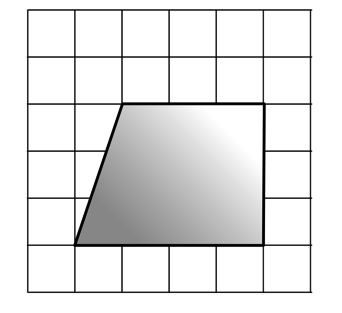
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

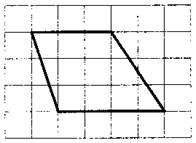
14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

источники:

http://ege.sdamgia.ru/search?search=%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D0%BF%D0%BB%D0%BE%D1%89%D0%B0%D0%B4%D1%8C%20%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BA%D0%BB%D0%B5%D1%82%D1%87%D0%B0%D1%82%D0%BE%D0%B9

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

Источник

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Ответ: 18.

Нахождение площадей многоугольников сложной формы

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Ответ: 10,5 .

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Квадратная решетка и координатная плоскость

В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

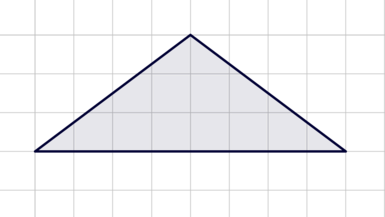
На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.

[/su_note]

Алгоритм решения:

Подсчитываем длину основания и высоты.
Записываем формулу вычисления площади.
Вычисляем площадь.
Записываем ответ.

Решение:

1. Подсчитываем длины основания и высоты:

основание = 6,

высота = 2.

2. Записываем формулу площади треугольника: S= ah|2.

3. Вычисляем площадь: S= 6∙2/2=6

Ответ: 6.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 3,5.

Ответ: 3,5.

Третий вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 4.

Ответ: 4.

Четвертый вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

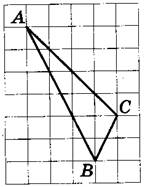
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

[/su_note]

Алгоритм решения:

Проведем перпендикуряры из вершин Аи С.
Построим биссектрису угла В.
Покажем, что биссектриса параллельна высотам.
Измерим длину биссектрисы.
Запишем ответ.

Решение:

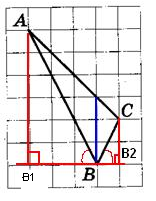
1. Проведем из вершин А и С отрезки АВ₁иСВ₂, перпендикулярные прямой, содержащей вершину В на рисунке.

2. Построим биссектрису угла B.

3. Рассмотрим треугольники АВВ₁ иВВ₂С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках

Это означает, что углы АВB₁ и СВB₂ равны, так как равны тангенсы этих углов.

Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.

Ответ: 3.

Пятый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

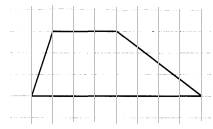
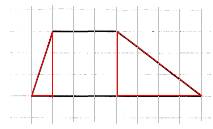
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

[/su_note]

Алгоритм решения:

Рассмотрим рисунок и измерим основания.
Проведем высоту.
Запишем формулу площади трапеции.
Вычислим площадь по формуле.

Решение:

1. На рисунке основания равны 3 и 8.

2. Опустим высоту. Она рана 3.

3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.

4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5

Следовательно, площадь данной трапеции равна 16,5.

Ответ: 16,5.

Даниил Романович | Просмотров: 12.3k

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на клетчатой бумаге

(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.

(blacktriangleright) В равных прямоугольниках равны диагонали.

(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).

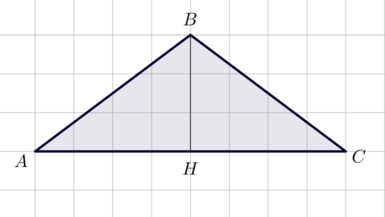
(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).

Задание
1

#3089

Уровень задания: Равен ЕГЭ

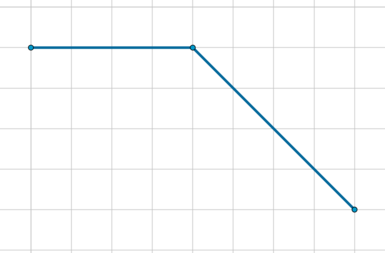
На клетчатой бумаге изображен угол. Найдите его градусную величину.

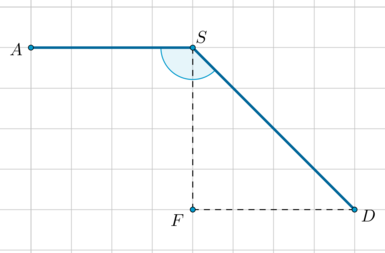
Обозначим этот угол (ASD). Отметим точку (F) так, чтобы получился прямоугольный (triangle SDF):

Тогда (angle ASD=angle ASF+angle FSD). Заметим, что (angle
ASF=90^circ). Заметим также, что (FS=FD), следовательно, (triangle
SDF) прямоугольный и равнобедренный, значит, его острые углы равны по (45^circ).
Следовательно, [angle ASD=90^circ+45^circ=135^circ.]

Ответ: 135

Задание
2

#3088

Уровень задания: Равен ЕГЭ

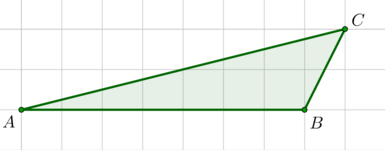
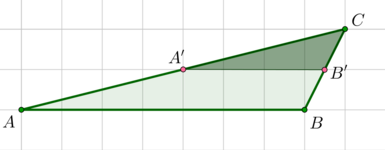
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите площадь треугольника (A’B’C), где (A’B’) – средняя линия, параллельная стороне (AB).

Пусть (A’in AC, B’in BC).

По свойству средней линии (triangle ABCsim triangle A’B’C) с коэффициентом подобия, равным (2). Следовательно, их площади относятся как коэффициент подобия в квадрате, то есть [dfrac{S_{ABC}}{S_{A’B’C}}=4] Высота (triangle ABC), опущенная из (C), равна (2), (AB=7). Следовательно, (S_{ABC}=frac12cdot 2cdot 7=7). Тогда [S_{A’B’C}=dfrac74=1,75.]

Ответ: 1,75

Задание
3

#3087

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите длину средней линии, параллельной стороне (AB).

Длина средней линии треугольника, параллельной стороне (AB), равна (frac12AB). Так как (AB=7), то средняя линия равна (3,5).

Ответ: 3,5

Задание
4

#3086

Уровень задания: Равен ЕГЭ

На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна (3).

Будем искать радиус вписанной окружности по формуле (S=pcdot r), где (S) – площадь, (p) – полупериметр.
Заметим, что треугольник равнобедренный: (AB=BC.)

Так как длина стороны клетки равна (3), то (AH=12, BH=9), следовательно, (AB=sqrt{AH^2+BH^2}=15.) Тогда [dfrac12cdot BHcdot AC=dfrac{AB+BC+AC}2cdot r quadRightarrowquad
r=4.]

Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна (1), а затем умножать полученный ответ на (3). Если бы длина одной клетки была равна (1), то (AH=4, BH=3), (AB=5) и (r=frac43). Тогда после умножения на (3) также получили бы (r=4). При решении задачи таким способом вычисления будут легче.

Ответ: 4

Задание
5

#297

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных миллиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть (0,5cdot (3 text{мм} + 4 text{мм})cdot 3 text{мм} = 10,5)мм(^2).

Ответ: 10,5

Задание
6

#298

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован треугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, тогда площадь нарисованного треугольника есть (0,5cdot 3)мм (cdot 4)мм (= 6)мм(^2).

Ответ: 6

Задание
7

#299

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.

У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна (0,5(2 text{мм} + 3 text{мм})cdot 4 text{мм} = 10) мм(^2).

Ответ: 10

Если выпускник готовится к сдаче ЕГЭ по математике и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит освоить принцип решения задач на клетчатой бумаге. Подобные планиметрические задания каждый год включаются в программу аттестационного испытания. Таким образом, справляться с задачами ЕГЭ на клетчатой бумаге должны все учащиеся, независимо от уровня их подготовки.

Полезная информация

Задания ЕГЭ на клетчатой бумаге часто решаются гораздо проще, чем задачи, для выполнения которых требуется применение аналитических методов. Чаще всего в подобных упражнениях необходимо найти площадь фигуры. Решить такие задачи можно, вспомнив основные теоремы и свойства трапеции, треугольника, шестиугольника и т. д.

Как подготовиться к экзамену?

Если задания ЕГЭ на клетчатой бумаге вызывают у вас трудности, обратитесь к образовательному порталу «Школково». С нами вы сможете повторить материал по темам, которые являются для вас сложными, например, векторы на координатной плоскости и таким образом восполнить пробелы в знаниях. В разделе «Теоретическая справка» представлена вся базовая информация. Ее наши специалисты подготовили и изложили в максимально доступной форме на основе богатого практического опыта.

Освоить принцип решения задач на клетчатой бумаге помогут упражнения, представленные в разделе «Каталог». Мы подготовили простые и более сложные задания. Тренироваться в их выполнении учащиеся из Москвы и других российских городов могут в онлайн-режиме.

Справившись с заданием, выпускники имеют возможность сохранить его в разделе «Избранное». Это позволит в дальнейшем вернуться к нему и, к примеру, обсудить алгоритм его решения со школьным преподавателем. База заданий на сайте «Школково» регулярно обновляется.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

27
Май 2013

Категория: 01 ГеометрияПланиметрия

01. Многоугольники. Вычисление длин и углов

2013-05-27
2022-09-11

Задача 1. На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.

Решение: + показать

Задача 2. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на

Решение: + показать

Задача 3. На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла.

Решение: + показать

Задача 4. На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.

Решение: + показать

Задача 5. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на

Решение: + показать

Задача 6. На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины B.

Решение: + показать

Задача 7. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его медианы, проведённой из вершины C.

Решение: + показать

Задача 8. Найдите высоту треугольника ABC, опущенную на сторону BC, если стороны квадратных клеток равны

Решение: + показать

Задача 9. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

Решение: + показать

Задача 10. Найдите периметр четырехугольника , если стороны квадратных клеток равны .

Решение: + показать

Задача 11. Найдите диагональ параллелограмма , если стороны квадратных клеток равны 1.

Решение: + показать

Задача 12. Найдите среднюю линию трапеции , если стороны квадратных клеток равны .

Решение: + показать

Задача 13. Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.

Решение: + показать

Задача 14. Найдите радиус окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите

Решение: + показать

Задача 15. На клетчатой бумаге с размером клетки 1×1 отмечены точки , и . Найдите расстояние от точки до прямой .

Решение: + показать

Задача 16. На клетчатой бумаге с размером клетки 1 x 1 отмечены две точки A и B. Найдите длину отрезка AB.

Решение: + показать

Задача 17. На клетчатой бумаге с размером клетки 1 см x 1 см изображен треугольник . Найдите длину его средней линии, параллельной стороне (в сантиметрах).

Решение: + показать

Задача 18. На клетчатой бумаге с размером клетки x изображён треугольник. Найдите радиус его описанной окружности.

Решение: + показать

Задача 19. Найдите радиус окружности, вписанной в изображенный на рисунке треугольник ABC,считая стороны квадратных клеток равными 1.

Решение: + показать

Вы можете пройти тест «Задачи №3. Многоугольник, вычисление длин и углов»

Автор: egeMax |

комментариев 10

Печать страницы

Источник