Как найти стороны вписанного прямоугольного треугольника

Треугольник вписанный в окружность

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac<1><2>ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

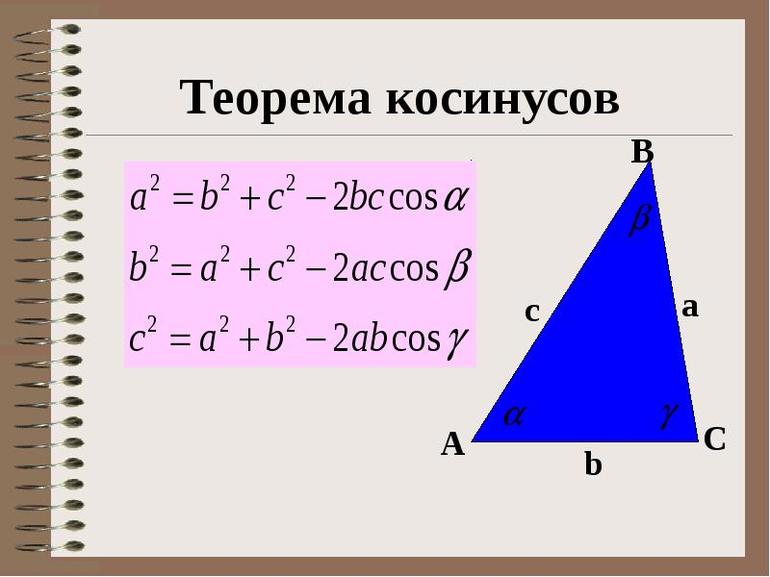
Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

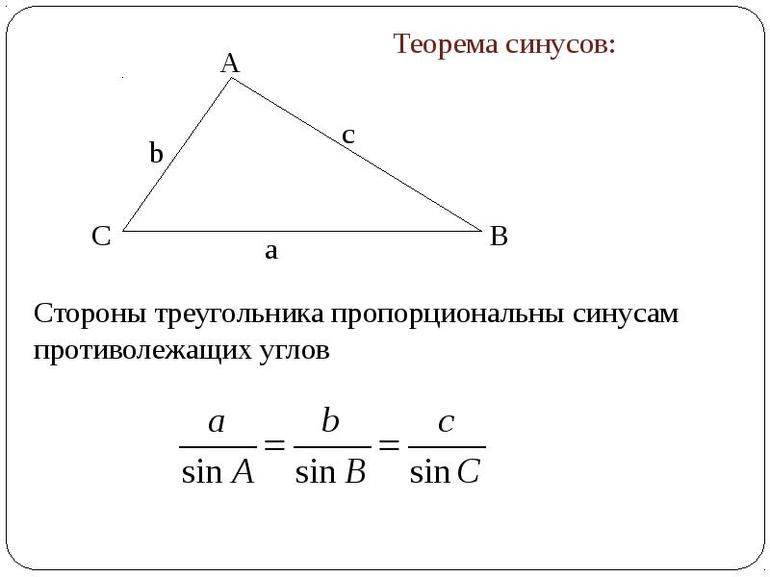
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — не диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:
   

   [ r = frac{S}{(a+b+c)/2} ]

2. Радиус вписанной окружности в треугольник,
   если известны площадь и периметр:
   

   [ r = frac{S}{frac{1}{2}P} ]

3. Радиус вписанной окружности в треугольник,
   если известны полупериметр и все стороны:
   

   [ r = sqrt{frac{(p-a)(p-b)(p-c)}{p}} ]

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:
   

   [ R = frac{AC}{2 sin angle B} ]

2. Радиус описанной окружности около треугольника,
   если известны все стороны и площадь:
   

   [ R = frac{abc}{4S} ]

3. Радиус описанной окружности около треугольника,
   если известны все стороны и полупериметр:

   [ R = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}} ]

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

   [ S = pr ]

2. Площадь треугольника вписанного в окружность,
   если известен полупериметр:

   [ S = sqrt{p(p-a)(p-b)(p-c)} ]

3. Площадь треугольника вписанного в окружность,
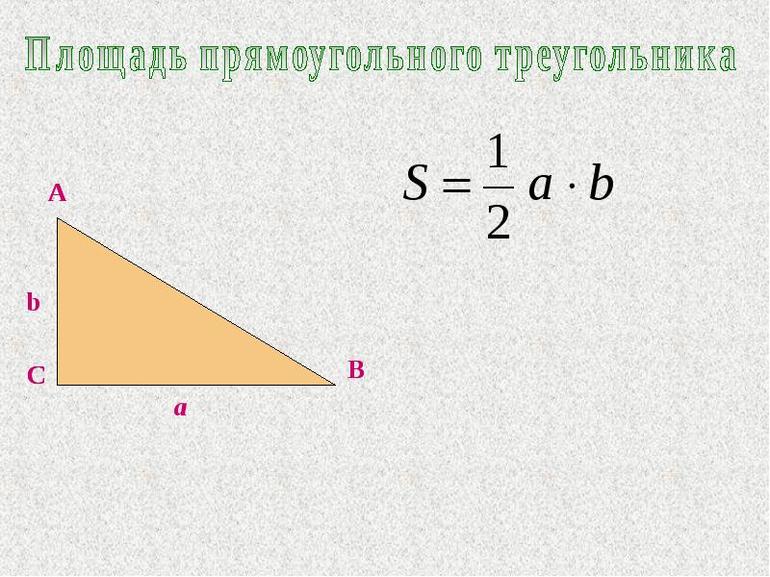
   если известен высота и основание:

   [ S = frac{1}2 ah ]

4. Площадь треугольника вписанного в окружность,
   если известна сторона и два прилежащих к ней угла:

   [ S = frac{a^2}{2cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} ]

5. Площадь треугольника вписанного в окружность,
   если известны две стороны и синус угла между ними:

   [ S = frac{1}{2}ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1.  Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

   [ P = a + b + c ]

2. Периметр треугольника вписанного в окружность,
   если известна площадь и радиус вписанной окружности:
   

   [ P = frac{2S}{r} ]

3. Периметр треугольника вписанного в окружность,
   если известны две стороны и угол между ними:

   [ P = sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) ]

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

   [ a = sqrt{b^2+c^2 -2bc cdot cos alpha} ]

2. Сторона треугольника вписанного в
   окружность, если известна сторона и два угла:
   

   [ a = frac{b · sin alpha }{sin β} ]

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

   [ l = frac{AB}{2} ]

2. Средняя линия треугольника вписанного в окружность,
   если известны две стороны, ни одна из них не является
   основанием, и косинус угла между ними:
   

   [ l = frac{sqrt{b^2+c^2-2bc cdot cos alpha}}{2} ]

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

   [ h = frac{2S}{a} ]

2. Высота треугольника вписанного в окружность,
   если известен сторона и синус угла прилежащего
   к этой стороне, и находящегося напротив высоты:

   [ h = b cdot sin alpha ]

3. Высота треугольника вписанного в окружность,
   если известен радиус описанной окружности и
   две стороны, ни одна из которых не является основанием:

   [ h = frac{bc}{2R} ]

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

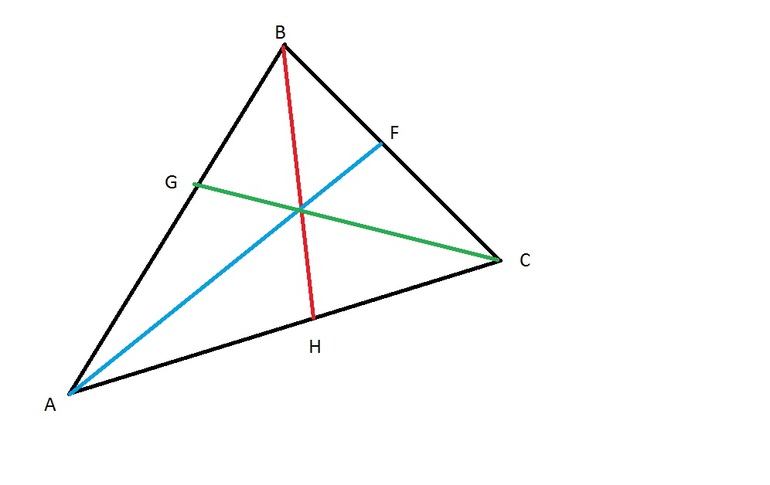
Дано: окружность и треугольник,
которые изображены на рисунке 2.

Доказать: окружность описана
около треугольника.

Доказательство:

1.  Проведем серединные
   перпендикуляры — HO, FO, EO.
2.  O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

Следовательно: окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Произвольный треугольник

Фигура с тремя углами является самым простым замкнутым объектом в геометрии. В общеобразовательных школах ее изучению уделяют наибольшее время, поскольку многие основные геометрические свойства заложены именно в ней. Построить ее несложно, для этого необходимо взять три точки на плоскости так, чтобы они не располагались на одной прямой. После этого следует попарно соединить их прямыми отрезками.

Треугольник произвольного типа состоит из следующих элементов:

• три вершины;
• три стороны, которые в общем случае имеют различную длину;
• одна вершина в совокупности с парой прилегающих к ней сторон образует угол, их в треугольнике три.

Помимо основных элементов, для этой фигуры существует множество дополнительных отрезков, которые имеют специальное название, например, медианы, биссектрисы, высоты.

Для рассматриваемой фигуры всегда справедливы три важных математических соотношения между ее длинами сторон и углами. Эти соотношения часто используют для решения разнообразных задач. К ним относятся следующие:

1. О сумме углов. Треугольник характеризуется тремя углами, сумма которых всегда составляет 180 градусов или пи радиан. Это свойство следует из характеристики евклидовой геометрии на плоскости. Его записывают так: ∠ A + ∠ B + ∠ C = 180 °, где символом ∠ обозначен угол при соответствующей вершине.
2. Теорема синусов. Словесная ее формулировка следующая: отношение длины стороны треугольника к синусу лежащего напротив нее угла является величиной постоянной для данной фигуры. Математически это утверждение записывается так: a/sinA = b/sinB = c/sinC, где буквами a, b и c обозначены длины сторон треугольника. Это выражение удобно использовать, когда по условию задачи известна одна сторона и два угла, и необходимо найти оставшиеся элементы фигуры.
3. Косинусов теорема. Она звучит так: квадрат стороны треугольника равен сумме квадратов двух оставшихся сторон за вычетом их удвоенного произведения, которое помножено на косинус угла между ними. Несмотря на несколько громоздкую формулировку, теорема имеет лаконичную математическую формулу: c ² = a ² + b ² — 2*a*b*cosC. Это выражение удобно применять, когда известны две стороны и угол в треугольнике.

Прямоугольная фигура

С незапамятных времен человечество интересовалось свойствами геометрических объектов. Одним из них был прямоугольный треугольник, который еще в Древнем Египте считался священным, поскольку обладал характерными для него особенностями (речь идет о фигуре, соотношение сторон которой находится в отношении 3:4:5). Большие достижения в области изучения геометрических свойств рассматриваемой фигуры имели философы античной Греции, среди которых выделяется имя Пифагора.

Составляющие элементы и теорема Пифагора

Поскольку речь идет о треугольнике, то для него также характерно наличие трех сторон и трех внутренних углов. Однако, в отличие от остальных фигур данного вида, прямоугольный треугольник имеет один угол равный 90 °. Остальные два угла всегда являются острыми, что следует из фиксированной суммы их значений (180 °).

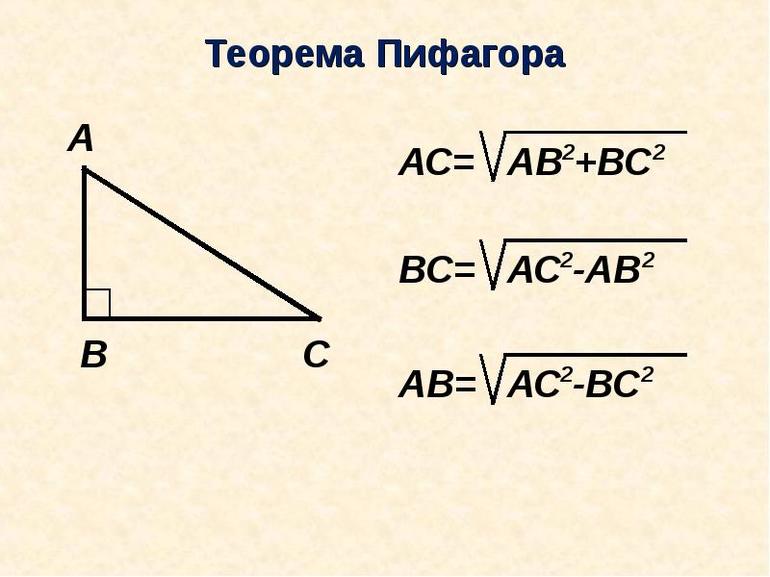
Чтобы узнать, как называются стороны прямоугольного треугольника, следует рассмотреть его рисунок.

Стороны a и b образуют прямой угол. Они называются катетами. Сторона c, которая лежит против угла 90 °, ограничена двумя острыми углами. Она носит название гипотенузы. Эти названия стоит запомнить, поскольку на них основаны все свойства и теоремы для этого типа треугольника.

Существует два вида рассматриваемой фигуры:

• равнобедренный;
• разносторонний.

В случае разностороннего прямоугольного треугольника стороны равны произвольным отрезкам, которые, однако, связывает теорема Пифагора. Катеты в этой фигуре отличаются друг от друга.

Касательно равнобедренного прямоугольного геометрического объекта можно сказать, что его катеты друг другу равны, но они никогда не равны гипотенузе. Острые углы в таком треугольнике составляют по 45 °, что легко доказать, применяя теорему синусов, и учитывая, что сумма трех углов соответствует 180 °.

Теорема косинусов для рассматриваемого треугольника произвольной формы вырождается в простое равенство:

c ² = a ² + b ² — 2*a*b*cosC ==>

c ² = a ² + b ² .

Оно получается потому, что косинус прямого угла равен нулю согласно свойству этой тригонометрической функции. Формулировка «квадрат гипотенузы в точности соответствует сумме квадратов катетов данного треугольника» носит название известной теоремы Пифагора. Чтобы ее доказать, не прибегая к теореме косинусов, следует провести некоторые геометрические построения.

Основные свойства

Несмотря на общие свойства, которыми обладает прямоугольный треугольник, и которые характерны для любой фигуры с тремя вершинами и тремя сторонами, для него существуют также присущие только ему особенности. Основными из них являются следующие:

1. Наличие двух острых углов, что видно из рисунка треугольника прямоугольного.
2. Длина гипотенузы всегда больше длины любого из катетов, при этом сумма длин последних всегда будет больше, чем одна гипотенуза.
3. Справедливость теоремы Пифагора.
4. Если один из острых углов равен 30 °, то противолежащий к нему катет ровно в два раза меньше длины гипотенузы.
5. Сумма длины гипотенузы и диаметра окружности, вписанной в треугольник, равна сумме длин катетов. Математически получается следующая запись: c + 2*r = a + b, здесь r — радиус вписанной в треугольник окружности. Получить это выражение можно легко, если применить теорему о вписанной в произвольный треугольник окружности, которая устанавливает связь между r, p и S: S = p*r, где S — площадь фигуры, p — ее полупериметр.
6. Чтобы понять, как найти основание прямоугольного треугольника, следует рассмотреть его катеты. Поскольку они перпендикулярны друг другу, то один из них может служить высотой, а другой основанием. Тогда площадь вычислится, как полупроизведение этих сторон: S = ½*a*b.
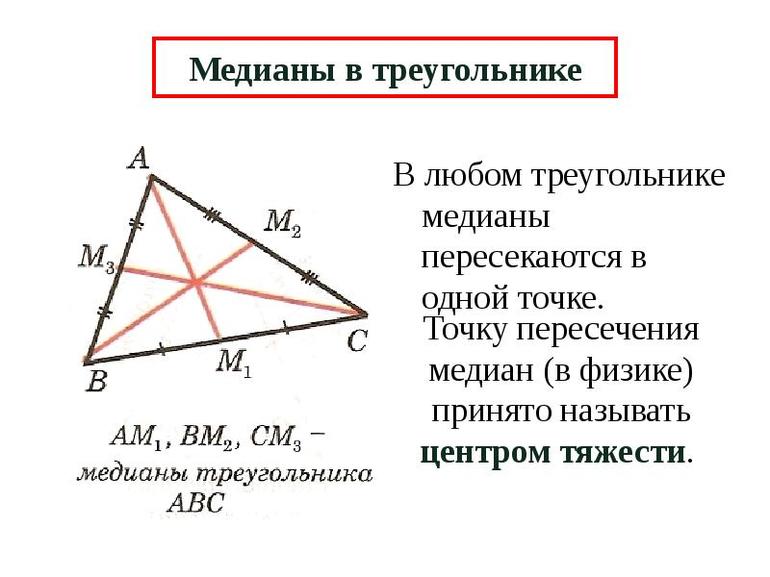
7. Медиана M делит прямой угол равнобедренного треугольника на две равные части, то есть является биссектрисой. Одновременно она является высотой, длина которой равна половине гипотенузы: M = ½*c. Это свойство справедливо для любого треугольника с прямым углом, а не только для равнобедренного.
8. Длину высоты h, которая проведена из вершины с прямым углом на основание-гипотенузу, можно найти по следующей формуле через катеты: h = a*b/(a² + b²)^0,5. Это равенство следует из формулы для площади фигуры.

Кроме названных свойств, следует отметить, что рассматриваемый геометрический объект является источником определения тригонометрических выражений (синуса, косинуса, котангенса и тангенса). Так, синусом угла ∠ A будет отношения противолежащего ему катета a к гипотенузе c, то есть sinA = a/c. Косинусом этого угла будет отношения ближайшего или прилежащего к нему катета к стороне c: cosA = b/c. Составлены целые таблицы этих функций, которые активно используются при решении геометрических проблем.

Способы нахождения длины стороны

Рассматриваемая фигура обладает достаточно большим количеством геометрических свойств, которые имеют математическое выражение в виде формул. Также для нее применимы особенности тригонометрических функций и общие формулы для треугольников общего типа. Весь этот набор равенств можно использовать для нахождения любой неизвестной стороны прямоугольной фигуры. Чаще всего встречаются задачи следующего типа:

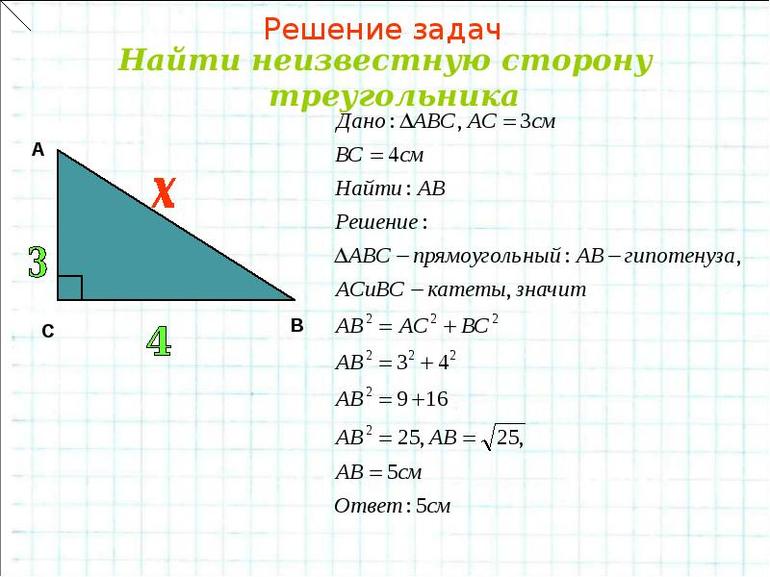
1. Известны две любые стороны. Независимо от того, неизвестен один из катетов или гипотенуза, найти эту сторону легко с использованием теоремы Пифагора. Пример для катета a выглядит так: a = (c ² — b ² )^0,5.
2. По известному острому углу и произвольной стороне. В этом случае любую из двух оставшихся неизвестных сторон треугольника легко вычислить с помощью соответствующей тригонометрической функции. Например, известен угол ∠ B и катет a, тогда: b = a*tgB, с = a/cosB.
3. По катету и высоте, проведенной из прямого угла. Для решения этой задачи сначала необходимо найти острый угол исходного треугольника, который определяется с помощью тригонометрической функции синуса. Как только он станет известен, задача сводится к типу 2.
4. По периметру и стороне. Эта задача имеет более сложный характер, чем описанные ранее. Решается она с помощью той же теорема Пифагора, но с применением теории квадратных уравнений.
5. Наконец, самый сложный вариант задачи на нахождение произвольного катета по известным площади фигуры и высоте, которая опущена из прямого угла. Здесь также необходимо использовать теорию решения квадратных уравнений, но в дополнение к этому следует использовать замену переменных.

Пусть площадь треугольника составляет 60 см ² , а опущенная высота из острого угла равна 8 см. Необходимо посчитать, какие длины имеют катеты и гипотенуза.

Если внимательно прочитать условие задачи, то можно увидеть, что сама высота является одним из катетов, поскольку опущена она на основание не из прямого, а из острого угла. Пусть катет a = 8 см. Сторона b вычисляется по формуле для площади:

S = ½*a*b ==>

b = 2*S/a = 2*60/8 = 15 см.

Определить гипотенузу легко по формуле Пифагора:

c = (a ² + b²)^0,5 = (8² + 15²)^0,5 = 17 см.

Прямоугольный треугольник обладает набором свойств, которые позволяют применить к нему знания тригонометрии, чтобы вычислить длину неизвестного катета или гипотенузы. При этом часто используемой формулой для решения геометрических задач является теорема Пифагора.

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b — катеты, с — гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b — катеты, с — гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a — искомая сторона, S — площадь треугольника.

2) Найти сторону через высоту

где a — искомая сторона,h — высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a — искомая сторона,r — радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a — искомая сторона,R — радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a — искомая сторона, b — известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Рассмотрим важные теоремы, которые помогут нам при решении задач.

Теорема 1. Вокруг любого треугольника можно описать окружность, причем только одну. Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.

Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.

Доказательство этой теоремы здесь: Свойство серединных перпендикуляров.

Теорема 2. В любой треугольник можно вписать окружность, причем только одну. Ее центром является точка пересечения биссектрис треугольника.

Доказательство теоремы здесь: Свойства биссектрис треугольника.

Теорема 3. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.

Доказательство:

Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Его доказательство можно найти здесь: Свойство медианы прямоугольного треугольника.

Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.

Теорема 4.

Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.

Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.

Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.

Теорема 5. Радиус окружности , вписанной в прямоугольный треугольник с катетами и и гипотенузой , вычисляется по формуле:

Доказательство теоремы здесь: Радиус окружности, вписанной в прямоугольный треугольник.

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Напомним определение правильного многоугольника:

Правильным называется многоугольник, все стороны и все углы которого равны. Центры вписанной и описанной окружностей правильного многоугольника находятся в одной точке.

Из этого определения, понятно, что правильный треугольник – равносторонний. Для решения такого треугольника полезно уметь выводить формулы радиусов вписанной и описанной окружностей.

Теорема 6.

Для правильного треугольника со стороной а радиус описанной окружности равен

А радиус окружности, вписанной в правильный треугольник, равен

Докажем эту теорему.

У равностороннего треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.

Пусть в правильном треугольнике стороны , точка О – центр вписанной и описанной окружностей, — медианы и высоты. По свойству медиан треугольника, отрезки в точке О делятся в отношении 2 : 1, считая от вершин. Тогда

Получаем, что

Из треугольника АВН получаем, что длина стороны

Тогда

Значит, формула радиуса окружности, описанной около правильного треугольника —

Формула радиуса окружности, вписанной в правильный треугольник

Как видим, часто геометрическая задача решается с помощью несложных формул, и помогает в этом алгебра.

Разберем задачи ОГЭ и ЕГЭ по теме: Вписанные и описанные треугольники.

Задача 1, тренировочная. Периметр правильного треугольника АВС равен 15. Найдите радиус вписанной и описанной окружностей.

Решение:

Длина стороны равностороннего треугольника  равна

Радиусы – вписанной и – описанной окружностей можно найти по формулам:

где — сторона треугольника.

Значит,

Ответ:

Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.

Вот две полезные формулы для площади треугольника.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

,

где — полупериметр,

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Теорема синусов:

R — радиус описанной окружности

Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.

Решение:

Выразим площадь треугольника двумя разными способами:

где – полупериметр треугольника, a – его стороны.

Тогда , а диаметр окружности равен

Ответ: 8.

Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Решение:

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что .

Тогда .

В ответ запишем .

Ответ: 4.

Задача 4, ЕГЭ. В треугольнике сторона равна  , а угол равен . Найдите радиус описанной около этого треугольника окружности.

Решение:

По теореме синусов

Тогда

Ответ: 7.

Задача 5, ЕГЭ. В треугольнике угол А равен , а угол В – . Найдите радиус окружности, описанной около треугольника , если сторона равна 10.

Решение:

Зная, что сумма углов треугольника равна , найдем угол С.

По теореме синусов

Значит,

Ответ: 10.

Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

Ответ: 150.

Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем .

Тогда .

Ответ: 25.

Задача 8, ОГЭ. В равнобедренном треугольнике основание равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.

Решение:

Высота , проведенная к основанию , является медианой. Значит, .

находится по теореме Пифагора из треугольника :

Периметр треугольника – это сумма длин сторон, т.е.

Площадь треугольника

Радиус вписанной окружности r найдем по формуле

Ответ:

Задача 9, ОГЭ. Стороны и треугольника равны 6 и соответственно, угол . Найдите диаметр окружности, описанной около треугольника .

Решение:

Найдем длину стороны по теореме косинусов, используя длины сторон , и косинус угла В, противолежащего стороне :

Теперь воспользуемся теоремой синусов:

Значит, диаметр окружности, описанной около треугольника , равен 6.

Ответ: 6.

Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.

Решение:

Пусть длина радиуса описанной окружности , а длина радиуса вписанной окружности

Мы знаем, что , где – полупериметр,  – стороны треугольника.

Значит,

Отсюда

Тогда

Ответ: 11.

Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.

Решение:

Пусть радиус вписанной окружности , а гипотенуза

Мы знаем, что в прямоугольном треугольнике

Значит, отсюда

Площадь находится по формуле где – полупериметр,  – стороны треугольника.

Ответ: 24.

Рассмотрим также задачу из 2 части ЕГЭ по математике.

Задача 12. Точка О – центр вписанной в треугольник окружности. Прямая вторично пересекает описанную около треугольника окружность в точке Р.

а) Докажите, что

б) Найдите площадь треугольника , если радиус окружности, описанной около треугольника равен 10,

Решение:

а) Пусть О – центр вписанной окружности, значит, и – биссектрисы углов и соответственно, и

как вписанные углы, опирающиеся на одну и ту же дугу
Тогда

– внешний угол треугольника , поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.

Значит, Что и требовалось доказать.

б)  , следовательно, треугольник – равнобедренный, – основание,

Угол равен , значит,

По теореме синусов для треугольника :

Тогда отрезок равен отрезку , т.е. .

Найдем угол С из треугольника :

как вписанные углы, опирающиеся на дугу .

Площадь треугольника находится по формуле:

Ответ:

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн