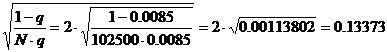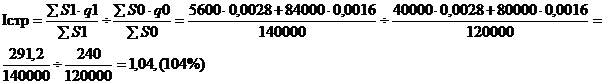Как найти страховую сумму пострадавших объектов

Имущественное страхование – это совокупность видов страхования, в которую входят обязанности страховщика выплачивать страховое возмещение страхователю в полном или частичном размере при наступлении неблагоприятного события, связанного с владением, пользованием или распоряжением объектами имущества.

На сегодняшний день, имущественное страхование в России – это отрасль страхования, в которой объектом страховых отношений выступают имущественные интересы и имущество в различных видах (например, здания, сооружения, оборудование и так далее). Рынок имущественного страхования в нашей стране развивается достаточно быстрыми темпами, и если в дальнейшем, в обществе не будет крупных переломных событий, то через некоторое время страхование может стать одним из основных факторов защиты интересов граждан и юридических лиц, которые обладают каким-либо имуществом.

Стихийные бедствия, их последствия и несчастные случаи нельзя предусмотреть в буквальном смысле. Закономерность этих событий можно проследить только в результате изучения массовой статистической информации, применяя соответствующие методы, основанные на теории вероятностей.

Для того чтобы рассчитать относительные и средние показатели имущественного страхования, необходимо определить основные нормативные значения и их содержание. Рассмотрим элементы абсолютных показателей [1, с.198].

Одним из основных показателей является страховое поле, то есть максимальное число объектов, которое может находиться в страховании. Показатель исчисляется в штуках и обозначается как N_max.

Если необходимо определить число застрахованных объектов или количество заключенных договоров страхования за период, чаще периодом страхования является год, то данный показатель именуется страховым портфелем, измеряется в штуках и обозначается как N.

Показатель S определяет страховую сумму застрахованных объектов и измеряется в денежных единицах, чаще всего в тысячах рублей.

Сумма поступившего страхового платежа или страховой взнос измеряется в денежных единицах  и обозначается как V.

Показатель, который определяет число страховых случаев, обозначается как n_c и показывает, сколько раз наступал страховой случай за некоторый период времени.

Число пострадавших объектов является немаловажным показателем в страховании, его значение определяет, сколько объектов пострадало за определенный период времени, измеряется в штуках и обозначается как n_п.

Общая страховая сумма пострадавших объектов обозначается как S_п и показывает итоговую сумму пострадавших объектов, в результате наступления неблагоприятного события.

Одним из центральных показателей является сумма выплаченного страхового возмещения, обозначается как W, то есть денежное вознаграждение страхователю при нанесении ущерба объекту страхования, измеряется в денежных единицах, чаще всего в тысячах рублей [2].

Рассмотрев основные абсолютные показатели, выделим относительные коэффициенты в имущественном страховании с их значениями [3, с.68-71].

Степень охвата страхового поля определяет долю объектов, которые застрахованы, от максимально возможного числа объектов и показывает на каком уровне развито добровольное страхование, коэффициент определяется по формуле (1):

d = N / N_max ,                                                                  (1)

где d – степень охвата страхового поля, %;

      N – число заключенных договоров, шт.;

      N_max – страховое поле, шт.

Следующий коэффициент обозначается как доля пострадавших объектов, который показывает отношение к общему числу застрахованных объектов, расчет величины представлен в формуле (2):

d_n = n_п / N ,                                                                  (2)

где d_n – доля пострадавших объектов, %;

      n_п – число пострадавших объектов, шт.

Рассмотрим относительный коэффициент, который показывает страховой платеж на 1 рубль страховой суммы, показатель определяет тарифную ставку страхования имущества и рассчитывается по формуле (3):

U = V/ S ,                                                                    (3)

где U – коэффициент страхового платежа на 1 рубль, %;

      V – страховой взнос, тыс.руб.;

      S – страховая сумма застрахованных объектов, тыс.руб.

Частота страховых случаев определяет количество страховых случаев, которое приходится в 100 или 1000 единиц застрахованных объектов. Другими словами, это вероятность гибели или повреждения имущества, которое застраховано, данный коэффициент всегда больше единицы, представлен в формуле (4):

d_c = n_с / N ,                                                                   (4)

где d_c – частота страховых случаев, %;

      n_c – число страховых случаев, раз.

Коэффициент, который показывает уровень опустошительности страхового случая, по-другому называется коэффициент кумуляции риска. Показатель определяет количество объектов, которое пострадало в одном случае страхования, рассчитывается по формуле (5):

k_p = n_п / n_c ,                                                                   (5)

где k_p – коэффициент кумуляции риска, %.

Коэффициент выплат страхового возмещения или норма убыточности определяет, сколько копеек может быть выплачено страхователю в качестве страхового возмещения с каждого внесенного рубля. Если данный показатель больше единицы, то страхование имущества не принесет дохода и будет убыточным. Рассматривая коэффициент в динамике, должна наблюдаться тенденция к уменьшению, расчет показателя представлен в формуле (6):

k_в = W / V,                                                                   (6)

где k_в – норма убыточности, %;

      W – сумма выплаченного страхового возмещения, тыс.руб.

Коэффициент ущербности или полнота уничтожения пострадавших объектов показывает удельный вес суммы, которая подлежит возмещению к общей страховой сумме пострадавших объектов при наступлении неблагоприятного события. Если коэффициент меньше единицы, то ущерб будет возмещен частично, если равен единице, то ущерб равен первоначальной стоимости застрахованного имущества, то есть полное возмещение ущерба. Показатель рассчитывается по формуле (7):

k_y = W / S_n,                                                                  (7)

где k_y – коэффициент ущербности, %;

      S_п – страховая сумма пострадавших объектов, тыс.руб.

Коэффициент уровня убыточности страховых сумм определяет количество рублей, которое возмещается на каждый рубль страховой суммы, рассчитывается по формуле (8):

q = (W / S) х 100 ,                                                             (8)

где q – коэффициент уровня убыточности страховых сумм, %.

Абсолютная сумма дохода страховой компании характеризует значение суммы дохода страховой организации в абсолютном отношении и рассчитывается по формуле (9):

∆ =V – W,                                                                                 (9)                                      

где ∆ – абсолютная доходность страховой компании, руб.

Относительную доходность, то есть процент дохода страховой компании можно рассчитать по формуле (10). Коэффициент показывает доходность страховой организации в относительной величине и определяется как:

k_д = (V – W) / V,                                                             (10)

где k_д – относительная доходность организации, %.

Рассмотрев основные относительные коэффициенты, необходимо ознакомиться со средними коэффициентами в имущественном страховании, которые представлены ниже [3, с.72-73].

Одним из средних коэффициентов является средняя страховая сумма имущества, которое застраховано от неблагоприятных событий, величина показателя определяет отношение страховой суммы застрахованных объектов к общей сумме страхового портфеля, рассчитывается по формуле (11):

S_ср  = (∑S) / (∑N),                                           (11)

где  S_ср   — коэффициент средней страховой суммы имущества, %.

Средний размер страхового взноса рассчитывается как отношение суммы поступившего страхового взноса (платежа) к сумме страхового портфеля, формула (12) представлена ниже:

V_ср  = (∑V) / (∑N),                                                                     (12)

где V_ср  — коэффициент среднего размера страхового взноса, %.

Коэффициент среднего страхового возмещения (средней страховой суммы выплат) представлен в формуле (13). Показатель определяет соотношение суммы выплаченного страхового возмещения к общему числу пострадавших объектов, рассчитывается следующим образом:

W_ср  = (∑W) / ∑(n_п),                                                                    (13)

где W_ср — коэффициент среднего страхового возмещения, %.

Средний уровень убыточности страховых сумм показывает отношение суммы выплаченного страхового возмещения к числу пострадавших объектов. Данный показатель должен быть меньше единицы, так как значение больше единицы означало бы недострахование, коэффициент рассчитывается по формуле (14):

q_ср  = (∑W ) / (∑S ,                                                          (14)

где  q_ср– коэффициент среднего уровня убыточности страховых сумм, %.

Коэффициент тяжести страховых событий определяет отношение средней суммы страховых выплат к величине средней суммы застрахованного имущества, характеризует ту часть страховой суммы, которая уничтожена, рассчитывается по формуле (15):

К_m= W_ср / S_ср ,                                                                (15)

где К_m – коэффициент тяжести страховых событий, %.

Средняя страховая сумма пострадавших объектов определяется в отношении средней страховой суммы пострадавших объектов к среднему числу пострадавших объектов и рассчитывается по формуле (16):

S_{п ср}= (∑S_п )/ (∑n_п ),                                                        (16)

где S_{п ср} — средняя страховая сумма пострадавших объектов, руб.

Средний показатель полноты уничтожения объектов или коэффициент ущербности в среднем соотношении рассчитывается как отношение средней суммы выплаченного страхового возмещения к средней страховой сумме пострадавших объектов, если коэффициент равен единице, то объекты уничтожены в полном объеме, показатель представлен в формуле (17):

k_{y ср}=  (∑W)/(∑S_п),                                                         (17)

где k_{y ср}  — коэффициент ущербности, %.

Таким образом, мы рассмотрели расчет абсолютных, относительных и средних показателей, которые применяются в качестве анализа имущественного страхования.

Библиографический список

1. Сплетухов, Ю.А. Страхование / Ю.А. Сплетухов. – М.: Инфра-М, 2013. – 312 с.
2. Дианов, Д.В. Статистика финансов и кредита (для бакалавров). [Электронный ресурс] / Д.В. Дианов, Е.А. Радугина, Е.Н. Степанян. — Электрон. дан. — М. : КноРус, 2012. — 328 с. — Режим доступа: http://e.lanbook.com/book/53546  (дата обращения: 14.12.2016 года)
3. Грибанова, Н.А. Совершенствование методики определения эффективности имущественного страхования / Н.А. Грибанова // Финансы и кредит. – 2015. – № 47. – С. 67-73

---

Количество просмотров публикации: Please wait

Все статьи автора «Быкова Наталья Николаевна»

---

Подборка по базе: Петроченко БИН-20-02 задачи по гражд. праву.docx, Кравцова Обработка аудиофайлов для решения профессиональных зада, Кравцова Обработка аудиофайлов для решения профессиональных зад, контрольные вопросы задачи по Политология.docx, 2 задача курсовой по сопромату.doc, Решение кейсовой задачи по теме.docx, Задачи оптимизации (поиск решения) в ред эле табл.pdf, Еще задачи ВПТ.pdf, бх задачи.docx, управленческие решения.docx

---

Задачи для самостоятельного решения
Задача 1. Проведите анализ состояния и уровня страхования в региональном аспекте и выберите наименее убыточный регион по следующим показателям: коэффициенту ущерба, тяжести риска и убыточности страховой суммы. Исходные данные приведены в таблице 1.

Таблица 1

Исходные данные по регионам

Показатели	Регион А	Регион Б
Число застрахованных объектов, ед.	2235	1256
Страховая сумма застрахованных объектов, руб.	421056	441256
Число пострадавших объектов, ед.	754	359
Страховая сумма по всем поврежденным объектам, руб.	72127	93174
Страховое возмещение, руб.	34587	38124
Число страховых событий, ед.	427	271
коэффициент ущерба	47,95	40,91
коэффициент тяжести риска	50,78	73,87
коэффициент убыточности страховой суммы	8,21	8,64

Решение:

Определим коэф. ущерба для каждого региона по формуле

Ку=В/См, где В-сумма страхового возмещения , См – страховая сумма по всем поврежденным объекта.

Регион А: Ку=34587/72127=0,4795 или 47,95%

Регион Б:Ку=38124/93174=0,4091 или 40,91%

Определим коэффициенты тяжести риска:

Тр=Со/Сс, Со- средняя страховая сумма на один пострадавший объект, Сс- средняя страховая сумма на один застрахованный объект.

Регион А:Тр= 72127:754/421056:2235=95,66/188,39= 0,5078 или 50,78%

Регион Б: Тр=93174:359/441256:1256=259,54/351,32= 0,7387 или 73,87%

Определим коэффициенты убыточности страховой суммы:

Ус=В/С, где С- страховая сумма всех объектов страхования

Регион А:Ус=34587/421056*100=8,21 руб. на 100 руб. страховой суммы

Регион Б:Ус= 38124/441256*100=8,64руб. на 100руб. страховой суммы . Представим полученные коэффициенты в таблице и сравним их. Наименее убыточным является регион Б.

Задача 2. Определение расчетных показателей страховой статистики и их оценка.

Таблица 2

Расчет статистических показателей по имущественному страхованию

№ п/п	Показатели	Условное обозначение	Величина показателя
1	Число объектов страхования, ед.	N	28 505
2	Частота страховых событий, ед.	e	12 548
3	Число пострадавших объектов в результате страховых событий, ед.	m	12 566
4	Сумма собранных страховых премий, тыс. руб.	p	865 122
5	Сумма выплаченных страховых возмещений, тыс. руб.	Q	421 031
6	Страховая сумма всех застрахованных объектов, тыс. руб.	Sn	6 014 728
7	Страховая сумма пострадавших объектов данной страховой совокупности, тыс. руб.	Sm	2 631 771
8	Частота страховых событий, ед. Чс = е/n; Чс < 1	Чс	0,44
9	Опустошительность страхового события (коэффициент кумуляции), ед. Кк =m/e; Кк > 1	Кк	1,001
10	Коэффициент убыточности (ущербности), ед. Ку = ∑ Q / ∑ Sm; Ку ≤ 1	Ку	0,16
11	Средняя страховая сумма на один объект (договор) страхования, тыс. руб. Сос = ∑Sn / n	Сос	211,006
12	Средняя страховая сумма на один пострадавший объект, тыс. руб. Спо = ∑Sm / n	Sп.o.	92,33
13	Тяжесть риска, тыс. руб. Tp = Спо / Сос	Tp	0,44
14	Убыточность страховой суммы (вероятность ущерба) Уs = ∑Q / ∑ Sn ; Уs < 1	Уs	0,07
15	Норма убыточности, % Ну = (∑Q / ∑р) × 100%; 0 < Ну < 1	Ну	0,49
16	Частота ущерба Чу = m / n; Чу < 1	Чущ	0,44
17	Тяжесть ущерба g = (∑Q / m) / (∑Sn / n)	Тущ	0,16

Требуется:

Рассчитать статистические показатели по имущественному страхованию.

Сделать анализ рассчитанных показателей.
Задача 3. Рассчитать относительные показатели по страховой компании, исходя из следующих абсолютных показателей:

Число застрахованных объектов – 2100.

Число страховых событий – 86.

Число пострадавших объектов – 104

Страховая сумма всех застрахованных объектов – 3150 млн. руб.

Страховая сумма пострадавших объектов – 124,8 млн. руб.

Страховое возмещение – 42,64 млн. руб.

Страховая премия – 47,25 млн. руб.

Решение.

Определение показателей по страховой компании «А».

1. Коэффициент ущербности

2. Коэффициент кумуляции риска

3. Вероятность наступления страхового случая

4. Коэффициент тяжести ущерба, вызванного страховым случаем

5. Убыточность страховой суммы

Задача 4. Рассчитайте показатели страхования по двум регионам:

Частота страховых событий на 100 единиц объектов.

Убыточность страховой суммы на 100 руб. страховой суммы.

Тяжесть ущерба.

Выберите наименее убыточный регион.

Таблица 1

Показатели по страхованию объектов

Показатели	Регион 1	Регион 2
Число застрахованных объектов, ед.	32000	4000
Страховая сумма застрахованных объектов, тыс. руб.	110000	30300
Число пострадавших объектов, ед.	9850	2100
Число страховых событий, ед.	8800	1950
Страховое возмещение, тыс. руб.	2050	3100
Страховая сумма по всем поврежденным объектам, руб.	10235	28950

Решение:

Определение показателей по страховой региона 1.

1. Коэффициент ущербности

2. Коэффициент кумуляции риска

3. Вероятность наступления страхового случая

4. Коэффициент тяжести ущерба, вызванного страховым случаем

5. Убыточность страховой суммы

Определение показателей по страховой региона 2.

1. Коэффициент ущербности

2. Коэффициент кумуляции риска

3. Вероятность наступления страхового случая

4. Коэффициент тяжести ущерба, вызванного страховым случаем

5. Убыточность страховой суммы

Задача 5. Рассчитайте относительные показатели по страховой компании ООО «Омега», исходя из следующих абсолютных показателей:

-число объектов страхования – 2100;

-число страховых событий — 86;

-число пострадавших объектов в результате страховых событий — 110;

-сумма собранных страховых платежей – 3150 млн. руб.;

-сумма выплаченного страхового возмещения -43 млн. руб.;

-страховая сумма для любого объекта страхования – 47 млн. руб.;

-страховая сумма, приходящаяся на поврежденный объект наблюдаемой совокупности – 125 млн. руб.

Решение:

1. Коэффициент убыточности: Ку= страховое возмещение / страховая премия =47/125=0,376

2. Коэффициент кумуляции: Кк=110/86=1,28 объекта на одно страховое событие

3. Вероятность наступления страхового случая: Р=110/2100=0,05

4. Коэффициент тяжести риска, вызванного страховым случаем: Ктр=(47/110) /(3150/2100)=0,28

5. Убыточность страховой суммы: У= 47/3150*100=1,49%
Задача 6. Рассчитать частоту страховых событий, если число объектов страхования равно 36, число страховых событий – 12, число пострадавших объектов в результате страховых событий – 2.

Решение:

Частота страховых событий, ед. Чс = е/n= 36/12=3
Задача 7. Рассчитать опустошительность страхового события, или коэффициент кумуляции риска, если известно, что число страховых событий равно пяти, а число пострадавших объектов в результате страховых событий равно 8, при этом известно и число объектов страхования равно 4.

Кк=m/e

Кк= 8/4=2

Ответ: 2
Задача 8. Рассчитать коэффициент убыточности, если сумма выплаченного страхового возмещения составила 500000 руб., страховая

сумма для любого объекта страхования — 600000, а страховая сумма, приходящаяся на поврежденный объект равна 1000000 руб.

Ку= страховое возмещение / страховая премия.

Ку= 500 000/400 000=1,25

Ответ: 1,25
Задача 9. Рассчитать среднюю страховую сумму на один пострадавший объект, если число пострадавших объектов в результате страховых событий равно 10, страховая сумма, приходящаяся на поврежденные объекты составила 360000 руб., при этом число объектов страхования равно 40.

= ΣSm/m

= 360 000/40=9000

Ответ: 9000
Задача 10. Рассчитать убыточность страховой суммы, если сумма выплаченного страхового возмещения равна 660000 руб., а страховая сумма объектов страхования составила 1000000 руб., при этом сумма собранных страховых платежей 3300000 руб.

q= ΣQ/ ΣSn

q= 660 000/1000 000= 0,66

Ответ: 0,66
Задача 11. Рассчитать норму убыточности, если сумма выплаченного страхового возмещения равна 1200000 руб., при этом сумма собранных страховых платежей 2000000 руб.

Hy= ΣQ/ Σp*100

Hy= 1 200 000/ 2 000 000 * 100= 60%

Ответ: 60%.
Задача 12. Рассчитать тяжесть ущерба по следующим данным:

— сумма выплаченного страхового возмещения составила 2200000 руб.;

— страховая сумма объектов страхования составила 2420000 руб.;

— число объектов страхования равно 44;

— число пострадавших объектов в результате страховых событий -4.

Тяжесть ущерба g = (∑Q / m) / (∑Sn / n)

g =(2200000/4)/(2420000/44)=10
Задача 13. Рассчитать частоту ущерба, если наступило 6 страховых событий, при этом число пострадавших объектов в результате страховых событий равно 7, а число объектов страхования – 8.

Частота ущерба Чу = m / n; Чу < 1

Чу =7/8=0.875
Задача 14. Рассчитать относительные показатели по страховой компании К, исходя из следующих абсолютных показателей:

Число застрахованных объектов – 2100.

Число страховых событий – 86.

Число пострадавших объектов – 104

Страховая сумма всех застрахованных объектов – 3150 млн. руб.

Страховая сумма пострадавших объектов – 124,8 млн. руб.

Страховое возмещение – 42,64 млн. руб.

Страховая премия – 47,25 млн. руб.

Решение.

Определение показателей по страховой компании «А».

1. Коэффициент ущербности (см. формулу (4.6))

K_u=42.76/124.8=0.342

2. Коэффициент кумуляции риска (см. формулу (4.7))

K_k=104/84=1.2

3. Вероятность наступления страхового случая (см. формулу (4.8))

P=104/2100=0.05

4. Коэффициент тяжести ущерба, вызванного страховым случаем (см. формулу (4.9))

K_tu=(42.64/104)/(3150/2100)=0.273

5. Убыточность страховой суммы (см. формулу (4.10))

Q=42.64/3150*100=35%
Задача 15. По имущественному страхованию страховой организацией выплачено всего за год 46480 млн. руб., застраховано имущества на 24150620 млн. руб., получено премий — 46480 млн. руб., уплачено 21223 млн. руб. Определить горимость, горимость премии.

Решение

1. Определяем горимость руб.: Груб. = 46480/24150620 = 0,0019

Определяем горимость премии: Г прем. = 21223/46480= 0,457

Задача 16. Определить показатели страховой статистики при страховании от огня по следующей информации: застраховано рисков — 2111, число пожаров — 18, число горевших строений — 19, страховая сумма — 53 млн. руб., уплачено возмещений по всем пожарам — 29 млн. руб.; средний горевший риск — 8 млн. руб., средний застрахованный риск — 322 млн. руб.

Решение

1. Частота пожаров: Чпож = 18/2111 = 0,0085

2. Опустошительность пожаров: Опож = 19/18 = 1,056

3. Истребительность пожаров (полнота сгорания): Псгор= 29/53= 0,547

4. Отношение рисков: Ориск = 8/322 = 0,025

5. Горимость руб.: Где. = 0,0085х 1,056 х 0,547х 0,025= 0,00012 или при расчете на 1000 руб. — 0,12.

В
практике актуарных расчетов широко
используется страховая статистика.

Она
представляет собой систематизированное
изучение и обобщение наиболее массовых
и типичных страховых операций на основе
выработанных статистической наукой
методов обработки обобщенных итоговых
натуральных и стоимостных показателей,
характеризующих страховое дело.

Все
показатели, подлежащие статистическому
изучению, делятся на две группы:

• первая
  отражает процесс формирования страхового
  фонда,

• вторая
  — его использование.

Статистика
с помощью массового наблюдения, которое
велось за фактами и обстоятельствами
наступления тех или иных страховых
случаев в прошлом, получает данные для
установления статистической (априорной)
вероятности существования риска.

Анализ
полученного массива информации показывает
закономерность наступления страхового
случая и служит целям научного предвидения
будущего размера ущерба. Чем больше
число объектов наблюдения, тем более
достоверную основу для оценки будущего
развития событий представляет
установленная вероятность, так как
только в большой страховой совокупности
закон больших чисел может наиболее
точно проявить свое действие.

В
наиболее обобщенном виде страховую
статистику можно свести к анализу
следующих показателей:

• число
  объектов страхования — n,

• число
  страховых событий — e,

• число
  пострадавших объектов в результате
  страховых событий — m,

• сумма
  собранных страховых платежей — ∑p,

• сумма
  выплаченного страхового возмещения —
  ∑Q,

• страховая
  сумма для любого объекта страхования
  — ∑Sn,

• страховая
  сумма, приходящаяся на поврежденный
  объект наблюдаемой совокупности —
  ∑Sm.

Рассмотрим
расчетные показатели страховой
статистики.

Частота
страховых событий.

Она
равна соотношению между числом страховых
событий и числом застрахованных объектов
е/n, т. е. частота страховых событий
показывает, сколько страховых случаев
приходится на один объект страхования.

Указанное
соотношение может быть представлено и
количественно как величина меньше 1.
Это означает, что одно страховое событие
может повлечь за собой несколько
страховых случаев. Отсюда следует
терминологическое различие между
понятиями «страховой случай» и
«страховое событие». Страховым
событием может быть град, эпизоотия и
т.п., охватившие своим вредоносным
воздействием многочисленные объекты
страхования (случаи).

Опустошительность
страхового события (коэффициент кумуляции
риска)

представляет
собой отношение числа пострадавших
объектов страхования к числу страховых
событий, m/е; коэффициент кумуляции риска
показывает, сколько застрахованных
застигает то или иное событие, иначе
говоря, сколько страховых случаев
произойдет (наступит).

Минимальный
коэффициент кумуляции риска равен 1.
Если опустошительность больше 1, то
больше кумуляция риска и тем больше
цифровое различие между числом страховых
событий и числом страховых случаев. По
этой причине на практике страховые
компании при заключении договоров
имущественного страхования стремятся
избежать сделок, где есть большой
коэффициент кумуляции.

Коэффициент
(степень) убыточности (ущербности)

выражает
соотношение между суммой выплаченного
страхового возмещения и страховой
суммой всех пострадавших объектов
страхования, т. е. ∑Q/∑Sm. Данный показатель
меньше или равен 1. Превысить 1 он не
может, так как это означало бы уничтожение
всех застрахованных объектов более чем
один раз.

Средняя
страховая сумма на один объект (договор)
страхования
—

отношение
общей страховой суммы всех объектов
страхования к числу всех объектов
страхования, т.е. (∑Sn)/n. Объекты
имущественного страхования обладают
различными страховыми суммами. Поэтому
в актуарных расчетах применяются
различные методы подсчета средних
величин.

Средняя
страховая сумма на один пострадавший
объект

равна
страховой сумме всех пострадавших
объектов, разделенной на число этих
объектов, т.е. (∑Sm)/m. Каждый из пострадавших
объектов страховой совокупности имеет
свою индивидуальную страховую сумму,
которая отклоняется от средней величины.

Расчет
этих средних величин имеет большое
практическое значение. Отношение средних
страховых сумм называется в практике
страхования тяжестью риска и выражается
как [(∑Sm)/m]/[(∑Sn)/n]. С помощью этого
отношения производятся оценка и
переоценка частоты проявления страхового
события.

Убыточность
страховой суммы (вероятность ущерба)

равна
сумме выплаченного страхового возмещения,
разделенной на страховую сумму всех
объектов страхования, т. e.(∑Q/∑Sn).

Показателем
величины риска является число меньше
1. Обратное соотношение недопустимо,
так как это означало бы недострахование.
Убыточность страховой суммы можно также
рас сматривать как меру величины рисковой
премии.

Норма
убыточности
—

это
соотношение суммы выплаченного страхового
возмещения, выраженной в процентах, к
сумме собранных страховых платежей, т.
е. ∑Q/∑P 100. Для практических целей
исчисляют нетто-норму убыточности и
брутто-норму убыточности. Полученный
показатель может быть меньше, больше
или равен 1. Величина нормы убыточности
свидетельствует о финансовой стабильности
данного вида страхования.

Частота
ущерба

исчисляется
как произведение частоты страховых
случаев и опустошительности.

Данный
показатель выражает частоту наступления
страхового случая. Частота ущерба всегда
меньше единицы. При показателе частоты,
равном 1, налицо достоверность наступления
данного события для всех объектов.
Частота ущерба обычно выражается в
процентах или промилле к числу объектов
страхования.

Страховая
статистика требует установления
факторов, оказавших влияние на частоту
ущерба. Влияние отдельных факторов
является предпосылкой образования
рисковых групп.

Тяжесть
ущерба.

При
проведении некоторых видов страхования
возможно наступление страхового случая,
который причиняет ущерб, равный
действительной стоимости застрахованного
имущества. Такой ущерб принято называть
полным ущербом.

Однако
в большинстве видов имущественного
страхования ущерб может быть меньше
действительной стоимости имущества,
которое в результате страхового случая
не уничтожено, а только повреждено.
Такой ущерб принято называть частичным
ущербом.

Понятие
тяжести ущерба можно выразить математически
как произведение коэффициента ущербности.

(∑Q/∑Sm)
и отношения средних страховых сумм:
[(∑Sm)/m]/[(∑Sn)/n],

или
[(∑Q)/m]/[(∑Sn)/n] = g, где g — тяжесть ущерба,
делимое — вероятность ущерба (убыточность
страховой суммы), делитель —частота
ущерба.

Тяжесть
ущерба, связанная с наступлением
страхового случая, в любом виде страхования
обусловлена качествами, присущими
объекту страхования. Поскольку частота
ущерба показывает объекты страховой
совокупности, которые повреждены в
результате проявления риска, то тяжесть
ущерба показывает среднюю арифметическую
ущерба (среднего обеспечения) по
поврежденным объектам страхования по
отношению к средней страховой сумме
всех объектов.

Тяжесть
ущерба, которую также принято называть
степенью, объемом или размером ущерба,
вероятностью распространения ущерба,
показывает в любом случае, какая часть
страховой суммы уничтожена.

Тяжесть
ущерба снижается с увеличением страховой
суммы Это необходимо учитывать по каждой
рисковой группе, поскольку при страховании
по системе первого риска и наличии
франшизы недостаточно знать только
тяжесть ущерба для всей совокупности,
а нужно знать, кроме того, и распределение
ущерба по величинам, т. е. сколько ущерба
в количественном выражении, например,
меньше 10% страховой суммы и т.д.

С
помощью страховой статистики изучаются
частота ущерба и убыточность страховой
суммы по всем видам имущественного
страхования, по каждой рисковой группе.
Статистическими методами учитываются
причины ущерба, и их распределение во
времени и пространстве.

Статистическое
наблюдение в страховом деле ведется по
следующим основным признакам:

• время
  и место наступления ущерба,

• причина,

• страховое
  обеспечение,

• расходы
  на ликвидацию ущерба,

• страховая
  сумма и страховая стоимость,

• рисковая
  группа объекта страхования,

• распространяемость
  ущерба на другие объекты,

• результаты
  проведения предупредительных мероприятий.

На
основании этих данных могут быть
вычислены относительные цифры каждого
признака, составлены специальные
таблицы.

Обработка
статистических данных ведется с помощью
ЭВМ.

Обычно
имеется несколько признаков, которые
оказывают влияние на тяжесть ущерба.
Анализ этих факторов проводится с учетом
определенных закономерностей. Как
правило, на практике страховой взнос
относительно больше страховой суммы.
Страховая сумма является величиной,
которую страхователь устанавливает
более или менее произвольно. Если
предвидеть высокий субъективный риск
при крупной страховой сумме, то можно
полагать, что страховая сумма повлияет
на размер тяжести ущерба.

В
качестве измерителя она, безусловно,
оказывает влияние на величину страховой
премии, которая исчисляется в процентах
от страховой суммы. Доказано, что
необходимая премия зависит от
страховой суммы,
но только при условии, что чем больше
действительная стоимость, тем больше
и страховая сумма.

Возможно,
что величина тяжести ущерба находится
в равной зависимости от
действительной стоимости застрахованного
имущества.
Поскольку при страховании с учетом
действительной стоимости премия
увеличивается пропорционально увеличению
стоимости объекта, то предыдущее
утверждение будет справедливо, когда
объект страхования один и тот же.
Различные объекты страхования, наделенные
различными рисками, не будут иметь
равные страховые платежи, хотя
гипотетически их страховые суммы могут
быть одинаковы.

В
большинстве случаев размер тяжести
ущерба зависит от величины
объекта страхования.
Если провести исследование убыточности
при страховании средств транспорта,
можно установить, что величина полного
и частичного ущерба до известной степени
зависит от тоннажа судна. Платежи по
страхованию морских судов каско берутся
с учетом не только стоимости судов, но
и их тоннажа (дедвейта). Величина
застрахованного имущества также
оказывает влияние на размер тяжести
ущерба.

Возможно,
что некоторые признаки оказывают влияние
как на частоту,
так и на тяжесть ущерба.
В этом случае страховой платеж находится
в двойной зависимости.

При
калькулировании тарифной ставки
анализируются многочисленные факторы.

Любой
признак, который оказывает незначительное
влияние на осуществление риска, может
быть отброшен. Кроме того, некоторые
признаки могут быть образованы только
в малых группах, например, признак «пол»
имеет только две группы. В конце концов,
множество теоретически допустимых
комбинаций в группе признаков не
встречается на практике.

Если
есть единственная причина наступления
ущерба, то общие признаки необходимо
выразить в тарифе; последний должен
быть показателем общих, а не единичных
признаков, При страховании строений
таким общим признаком является величина
объекта как по частоте его, так и по
тяжести ущерба, При большом числе общих
признаков тарифная калькуляция становится
слишком объемной.

Если
есть несколько причин наступления
ущерба, абсолютные единичные надбавки
возможны, только когда они являются
следствием дополнительных причин и
независимы от всех признаков,
предусмотренных в базисном тарифе.

Процентные
надбавки

могут
применяться по любой отдельной причине,
но только относительно специальных
признаков. Не которые процентные надбавки
не могут быть каким-либо образом
компенсированы. Страховая премия может
быть разложена по нескольким надбавкам.

По
некоторым видам страхования величина
ущерба зависит от временной продолжительности
данного состояния, которое создается
страховым событием и называется
продолжительностью времени ущерба.

Продолжительность
времени ущерба
— один из факторов, от которых зависит
тяжесть ущерба. При страховании от
несчастных случаев тяжесть ущерба
зависит, кроме того, от степени утраты
трудоспособности. Этот второй
количественный признак называется
охватом ущерба.

При
наличии наблюдения за частотой ущерба
можно выяснить, какая часть страховой
премии определена неверно.

Если
имеется погрешность исчисления величины
ущерба, коррективы следует сделать
только в соответствующих группах.
Наличие систематических отклонений от
убыточности страховой суммы в течение
длительного времени свидетельствует,
что тариф не согласовывается с
действительным развитием ущерба.
Делается анализ эффективности
предупредительных мероприятий. При
случайных отклонениях следует проверить,
насколько они находятся в границах,
установленных с помощью теории
вероятностей.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Страховая статистика находит широкое применение в актуарных расчетах. Она фиксирует, систематизирует и изу­чает показатели наиболее типичных, массовых явлений в страховании и их изменение во времени (так называемые, динамические ряды показателей).

Статистика с помощью наблюдения фактов и обстоя­тельств наступления тех или иных страховых случаев в про­шлом получает данные для прогнозирования статистичес­кой вероятности страхового риска. Анализ полученной информации служит целям предвидения будущего размера ущерба. Чем больше число объектов наблюдения, тем дос­товернее основа для оценки будущего развития событий.

Для определения расчетных показателей страховой ста­тистики используют следующие исходные данные (в скобках даны иные обозначения, иногда приводимые в некоторых учебно-методических разработках):

1) число объектов страхования – n (N, a);   

2) страховая сумма для любого объекта страхования – SSn (S, b);

3) число страховых событий – е (L, c);

4) число пострадавших объектов в результате страховых со­бытий – т (M, d);

5) сумма выплаченного страхового возмещения – SQ (f);

6) сумма собранных страховых платежей – Sp;

7) страховая сумма, приходящаяся на поврежденный объект наблюдаемой совокупности – SSm.

Дадим краткую характеристику расчетным показателям страховой статистики.

Частота страховых событий:

          Чс < 1.

Частота страховых событий показывает, сколько стра­ховых случаев приходится на один объект страхования. Дан­ное соотношение может быть представлено количественно как величина меньше единицы. Это означает, что одно страховое событие может повлечь за собой несколько стра­ховых случаев. Отсюда следует различать понятия « страховой случай» и «страховое событие». Страховым событием могут быть град, эпидемия и т.п., влияющие своим воздействием на многие объекты страхования (страховые случаи).

Опустошительность страхового события, коэффици­ент кумуляции риска:

            

Коэффициент кумуляции риска показывает, сколько застрахованных объектов застигает то или иное событие, иначе говоря, сколько страховых случаев может состояться. Минимальный коэффициент кумуляции риска равен еди­нице. Если опустошительность больше единицы, то будет больше кумуляция риска и больше численное различие между числом страховых событий и числом страховых слу­чаев. Страховые компании при заключении договоров иму­щественного страхования стремятся избежать сделок, где есть большой коэффициент кумуляции.

Коэффициент убыточности, «степень убыточности», «степень ущербности»:

           

Данный показатель меньше или равен единице. Превы­сить единицу он не может, так как это означало бы унич­тожение всех застрахованных объектов более чем в один раз.

Средняя страховая сумма на один объект (договор) стра­хования :

.

Объекты имущественного страхования обладают различ­ными страховыми суммами. Поэтому в актуарных расчетах применяются различные методы подсчета средних величин.

Средняя страховая сумма на один пострадавший объект (Спо):

.

Каждый из пострадавших объектов страховой совокуп­ности имеет свою индивидуальную страховую сумму, ко­торая отклоняется от средней величины. Расчет этих сред­них величин имеет большое практическое значение.

Отношение средних страховых сумм называется в практике страхования тяжестью риска:

Тр = .

С помощью этого отношения производятся оценка и переоценка частоты проявления страхового события.

Убыточность страховой суммы, вероятность ущерба:

;          

Иное соотношение (Ус > 1) недопустимо, так как это означало бы недострахование. Убыточность страховой сум­мы можно также рассматривать как меру величины риско­вой премии.

Норма убыточности в процентах:

;          0 < Ну  < 1.

Для практических целей исчисляют нетто-норму убы­точности и брутто-норму убыточности. Величина нормы убыточности свидетельствует о финансовой стабильности данного вида страхования.

Частота ущерба:

;          Чу < 1.

Показатель выражает частоту наступления страхового случая. Частота ущерба всегда меньше единицы. При пока­зателе частоты, равном единице, налицо достоверность на­ступления данного события для всех объектов. Частота ущер­ба обычно выражается в процентах к числу объектов страхования. Страховая статистика требует установления фак­торов, оказавших влияние на частоту ущерба. Влияние отдельных факторов является предпосылкой образования рис­ковых групп.

Тяжесть ущерба (g). Различают полный и частичный ущербы.

Полный ущерб – когда при наступлении страхо­вого случая причиняется ущерб, равный действительной стоимости застрахованного имущества.

Частичный – когда имущество не уничтожено, а только повреждено. Обычно имеется несколько признаков, которые оказывают влияние на тяжесть ущерба: страховая сумма, величина объекта страхования (например, тоннаж судна), величина застрахованного имущества, продолжительность времени ущерба и некоторые другие.

Тяжесть ущерба, которую также называют степенью или размером ущерба, вероятностью распространения ущерба, показывает, какая часть страховой суммы уничтожена. Тяжесть ущерба можно выразить математически как про­изведение коэффициента ущербности (Ку = S Q / S Sm)  и отношения средних страховых сумм (S Sm/m : S.Sn/n) (тяжесть риска Тp):

g = Ку * Тp.

Тяжесть ущерба, связанная с наступлением страхового случая, в любом виде страхования обусловлена качества­ми, присущими объекту страхования. Если частота ущерба показывает объекты страховой совокупности, поврежден­ные в результате проявления риска, то тяжесть ущерба показывает среднюю арифметическую ущерба (среднего обеспечения) по поврежденным объектам страхования по отношению к средней страховой сумме всех объектов:

.

Тяжесть ущерба снижается с увеличением страховой суммы – это необходимо учитывать по каждой рисковой группе.

С помощью страховой статистики изучаются частота ущерба и убыточность страховой суммы по всем видам имущественного страхования, по каждой рисковой группе. Статистическими методами учитываются причины ущерба и их распределение во времени и пространстве.

Анализируя ежегодные статистические данные, страхов­щик имеет возможность выявлять положительные и нега­тивные факторы, оказывающие влияние на работу страхо­вой организации и принимать необходимые меры по обеспечению рентабельности страховых операций.

Страховой рынок подразделяется на отрасли имущественного, личного страхования, страхования ответственности и социального страхования.

Объектами имущественного страхования являются основные и оборотные фонды предприятий, организаций, домашнее имущество граждан.

К основным абсолютным показателям этой отрасли относятся:

страховое поле (N_max),

число застрахованных объектов (заключенных договоров) (N),

число страховых случаев (n_c),

число пострадавших объектов (n_П), страховая сумма застрахованного имущества (S), страховая сумма пострадавших объектов (Sп), сумма поступивших платежей (V, ), сумма выплат страхового возмещения (Q). На основе абсолютных показателей определяются различные относительные и средние показатели: частота страховых случаев, доля пострадавших объектов, опустошительность страховых случаев, полнота уничтожения, коэффициент выплат, убыточность страховой суммы, средние страховые суммы пострадавших и застрахованных объектов, средняя сумма страхового возмещения, средний коэффициент тяжести страховых событий и т.д.

Особое внимание уделяется расчеты страховых тарифов: нетто-ставки и брутто-ставки, динамике показателей работы страховых организаций.

Пример 1.

Имеются данные страховых организаций района о добровольном страховании имущества граждан:

Страховое поле (N_max)………………………………………………………………………256250

Число заключенных договоров (число застрахованных объектов) (N)……………… 102500

Сумма застрахованного имущества (S), тыс. руб……………………………………………..198350

Поступило страховых взносов (V, ), тыс. руб……………………………………….2800

Страховые выплаты (Q) тыс. руб…………………………………………………………..1680

Число пострадавших объектов (М)…………………………………………………………2050

Определить показатели, характеризующие деятельность страховых организаций.

Решение.

1.Степень охвата страхового поля:

d = N/ N_max = 102500 / 256250 = 0,4 или 40%.

2. Частота страховых случаев:

Чс = М / N = 2050 /102500 = 0,02 = 2%.

3. Средняя страховая сумма:

 = S / N = 198350 / 102500 = 1,9351 тыс. руб

4. Средняя сумма страхового взноса:

 = V / N = 2800 / 102500 = 27, 317 руб

5. Средняя сумма страховых выплат:

 = Q / n_П = 1680 / 2050 = 819,512 руб.

6. Коэффициент выплат:

К_В = Q / V = 1680 / 2800 = 0,60 = 60%.  Н_у=Q/ (норма убыточности).

7. Убыточность страховой суммы:

q = Q/S = 1680/198350 = 0,0085

8. Коэффициент тяжести страховых событий:

К_Т =  / = 819,512/1935,1 = 0,4235 = 42,35%.

9. Коэффициент финансовой устойчивости (с доверительной вероятностью 0,954, при которой t=2):

К_Ф = t *

Чем меньше данный коэффициент, тем устойчивее финансовое состояние.

10. Коэффициент финансовой устойчивости страхового фонда

К_Ф.У.= /Q = .2800/1680 = 1,66 = 166%

Пример 2.

Результаты работы страховых организаций в I полугодии характеризуется следующими данными:

Организация	Страховой взнос, V тыс. руб.	Коэффициент выплат, КВ	Выплаты W= КВ/V
1 2 3	400 500 700	0,5 0,6 0,2	200 300 140
Итого	1600	—	640

Определить:

1) средний коэффициент выплат;

2) абсолютную сумму дохода страховых операций;

3) относительную доходность.

Решение.

1. Коэффициент выплат рассчитывается по формуле:

К_В=Q/V.

    Средний коэффициент выплат составит:

= 40 %.

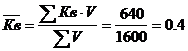
2. Абсолютная сумма дохода определяется разностью взносов и выплат:

 тыс. руб.

3. Относительная доходность (процент доходности) равна:

К_Д= 60%.

Пример 3.

Имеются данные страховых компаний о добровольном страховании имущества, тыс.руб.:

Район	Базисный период	Отчетный период
Страховая сумма, SО	Страховые выплаты, Q	Коэффициент убыточности, qО	Страховая сумма, S1	Страховые выплаты, Q1	Коэффициент убыточности, q1
1 2	40000 80000	112 128	0,0028 0,0016	56000 84000	140 168	0,0025 0,0020
Итого	120000	240	—	140000	380	—

Определить:

1) индивидуальные индексы убыточности по каждому району;

2) по двум районам индексы средней убыточности:

а) переменного состава,

б) постоянного состава,

в) структурных сдвигов.

Решение.

1. Темп изменения убыточности i_q=q₁/q_0.

По району 1: i_q1 = 0,8929 или 89,3%, т.е. убыточность снижается на 10,7%

По району 2: i_q2 = 1,25 – убыточность возросла на 25%.

2. а) индексы средней убыточности переменного состава равен:

I=,

т.е. средняя убыточность возросла на 10 % за счет влияния двух факторов: изменения коэффициента убыточности и размера страховых сумм.

Этот индекс можно представить иначе, заменив сумму выплат произведением страховой суммы на коэффициент выплат: W=Sq

Тогда индекс средний убыточности переменного состава примет вид:

I=,

б) индекс средней убыточности постоянного состава равен:

I_q== 105,8%

Т.е. средняя убыточность возросла на 5,81% за счет увеличения страховых выплат (убыточности).

в) влияние размера страховых сумм на динамик средней убыточности изучается с помощью индекса структурных сдвигов:

Средняя убыточность дополнительно повысилась на 4% за счет роста страховой суммы в первом районе.

Индекс структурных сдвигов можно определить, используя взаимосвязь индексов:

I_стр  = I/I_q = 1,1 / 1,058 = 1,04

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.