Как найти стрелу прогиба - Исправление недочетов и поиск решений вместе с Examum.ru

6.1. Понятие об упругой
линии. Прогиб и угол поворота.
Дифференциальное уравнение упругой
линии. Условие жесткости при изгибе

Чтобы судить о работе изгибаемых балок,
недостаточно знать только напряжения,
которые возникают в сечениях балки от
заданной нагрузки. Вычисленные напряжения
позволяют проверить прочность системы.
Однако весьма прочные балки могут
оказаться непригодными к эксплуатации
из-за недостаточной жесткости. Если
балка при нагружении сильно прогибается,
то при эксплуатации сооружения, имеющего
гибкие балки, появятся затруднения и,
кроме того, могут возникнуть колебания
балки с большими амплитудами, а вместе
с тем и значительные дополнительные
напряжения.

Под жесткостью
следует понимать способность
элеменов конструкций и деталей машин
сопротивляться внешним нагрузкам без
видимых деформаций.
Расчет на жесткость заключается в оценке
упругой податливости балки под действием
приложенных нагрузок и подбор таких
размеров поперечного сечения, при
которых перемещения не будут превышать
установленных нормами пределов. Для
выполнения такого расчета необходимо
научиться вычислять перемещения сечений
балки под действием любой внешней
нагрузки.

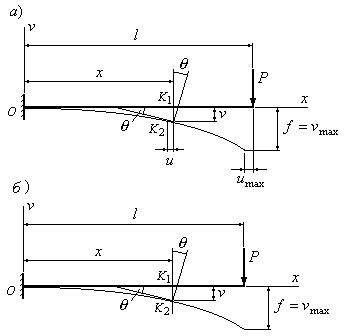
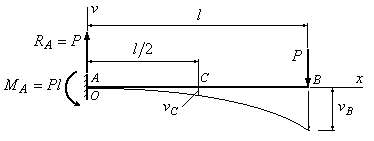
Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.

Точка
,
лежащая на оси в сечении, отстоящем не
расстоянииот начала координат, переместится в
точку.
Обозначим перемещение произвольной
точки оси бруса в направлении осичерез,
а перемещение вдоль оси бруса – через.
Если в точкепровести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол.
Одновременно на тот же угол повернется
сечение в точке.
Таким образом, три величины
,иявляются компонентами перемещения
произвольного поперечного сечения
балки. Перемещениецентра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
.

Угол
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью.

Рис.6.1

Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб
не должен превышать определенной доли
пролета:

Число
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величинапринимается равной 1000.

Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:

.
(6.1)

Во-вторых, горизонтальными
перемещениями
можно пренебречь, так как они существенно
меньше().
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.

Для определения полной картины деформаций
необходимо получить уравнение упругой
линии

Исходя из физической природы изогнутой
оси бруса, можем утверждать, что упругая
линия должна быть непрерывной и гладкой
кривой, следовательно, на протяжении
всей оси бруса должны быть непрерывны
функция и ее первая производная. Прогибы
и углы поворота и являются перемещениями
сечений балок при изгибе. Деформация
того или иного участка балки определяется
его кривизной.

При выводе формулы для нормальных
напряжений при изгибе нами была получена
связь между кривизной и изгибающим
моментом:

.
(6.2)

Из курса высшей математики известно
следующее уравнение кривизны плоской
кривой:

.
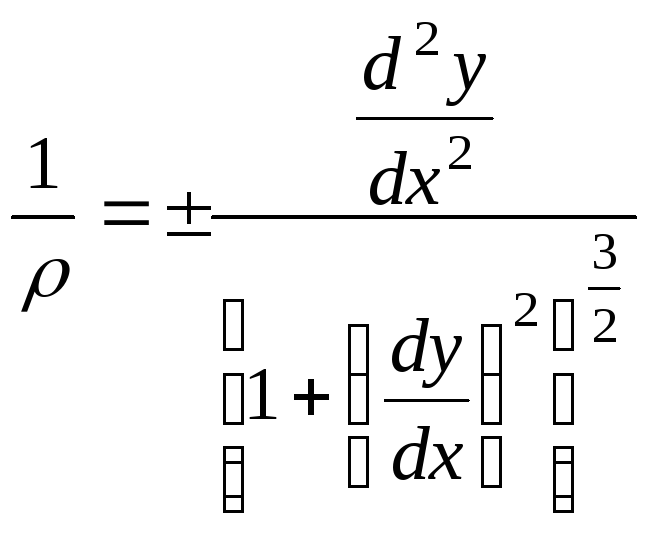
(6.3)

Подставляя значение
кривизны в равенство (6.2) и заменяя
координату
прогибом,
получим точное дифференциальное
уравнение упругой линии балки:

.
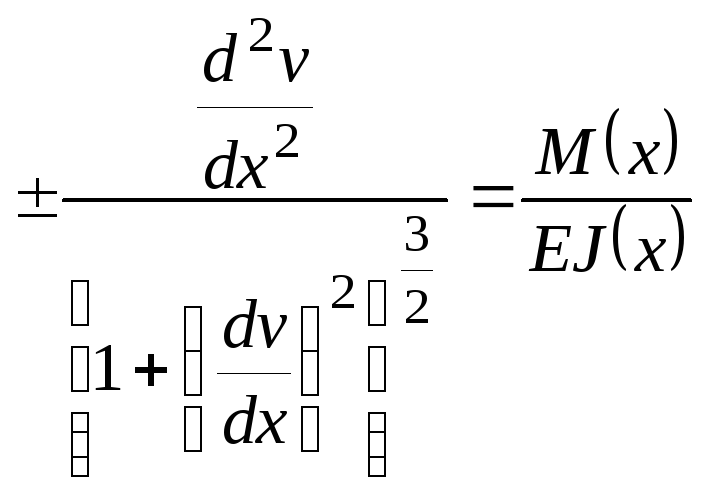
(6.4)

Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона
касательной к оси будут малы, квадратом
первой производнойпо
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение

(6.5)

Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны
может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
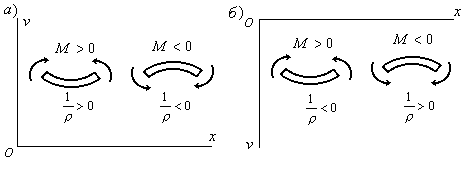
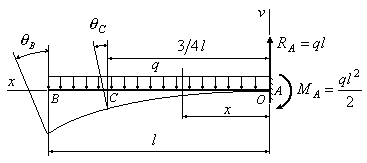
растянутые волокна. Так, например, для
случая, когда осьнаправлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.

Рис
6.2

Таким
образом, в случае, когда ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.

6.2. Метод непосредственного
интегрирования приближенного (основного)
дифференциального уравнения упругой
линии

Решая
задачу аналитическим методом, углы
поворота
и прогибывычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота:

,
(6.6)

где

постоянная интегрирования.

Интегрируя
второй раз, получим выражение для прогиба
:

,
(6.7)

где
и
постоянные интегрирования.

Для
вычисления интегралов, входящих в (6.6)
и (6.7), необходимо сначала написать
аналитические выражения для изгибающего
момента и жесткости. Постоянные
интегрирования находятся
из граничных условий,
которые зависят от условий перемещения
границ участков балки.

Рассмотрим несколько
примеров применения метода непосредственного
интегрирования приближенного уравнения
упругой линии балки.

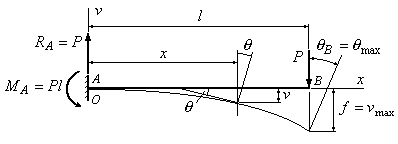
Пример
6.1. Определить
стрелу прогиба и угол поворота сечения
В балки, изображенной на рис.6.3.

Рис.6.3

Решение:

1. Из условий
равновесия определяем опорные реакции:

;
.

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получаем:

.
(а)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(б)

Так как в заделке прогиб и угол поворота
равны нулю, то для определения постоянных
интегрирования граничные условия имеют
вид:

при
;
при.

Из
уравнения (а) видно, что постоянная
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а),
находим.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
,
получаем.

Таким образом,
получаем следующие выражения для прогиба
и угла поворота:

Подставляя
в первое уравнение
,
найдем стрелу прогиба:

Подставляя
во второе уравнение
,
найдем максимальный угол поворота

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.

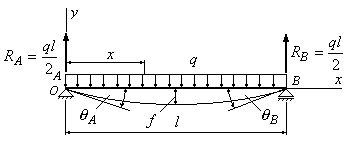
Пример
6.2. Определить
стрелу прогиба двухопорной балки и углы
поворота опорных сечений А и В (рис.6.4).

Рис.6.4

Решение:

1. Из условий
равновесия определяем опорные реакции:

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получим:

.
(в)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(г)

Постоянные
интегрирования найдем из граничных
условий:

при
;
при.

Подставляя
в уравнение (г)
и приравнивая прогиб нулю, получим;
подставляя в это же уравнение,
находим постоянную интегрирования:

Найденные значения
постоянных интегрирования подставим
в уравнения (в) и (г) и получим уравнения
углов поворота и прогибов:

;

Подставляя
ив первое уравнение, получим углы поворота
соответственно сечений А и В:

;

В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение
,
получим:

Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение В повернулось
против часовой стрелки.

Пример
6.3. В сколько
раз прогиб в сечении В на конце изображенной
на рис.6.5 балки, больше, чем прогиб в
сечении С
посредине
балки?

Рис.6.5

Решение:

Воспользуемся
результатами, полученными в примере
6.1. Запишем окончательное выражение для
прогиба:

и подставим в это
уравнение координаты точек С и В. Получим:

при
;

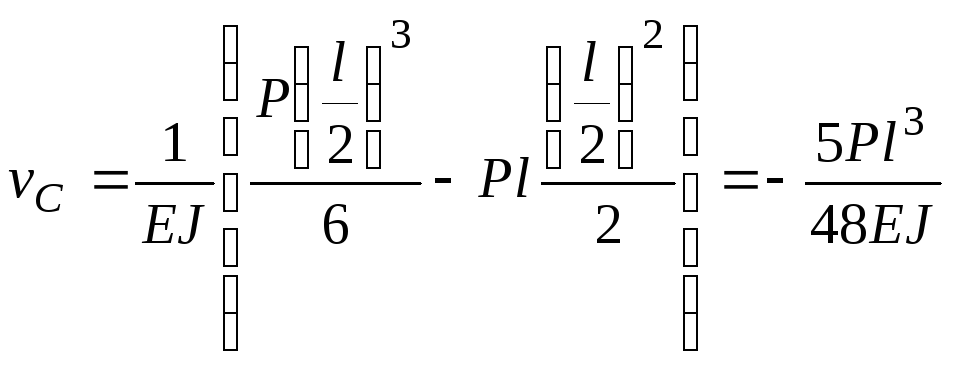
при
.

Сравнивая полученные
величины прогибов, приходим к выводу,
что прогиб в сечении В больше, чем прогиб
в сечении С в 3,2 раза:

Пример
6.4. В сколько
раз угол
поворота сечения
А
на конце изображенной на рис.6.6 балки
больше, чем угол поворота сечения В на
расстоянии четверти пролета от левого
конца балки?

Решение:

1.
Находим реакции: ;.

2.
Выбираем начало координат
на правом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
влево.

Рис.6.6

3.
Записываем выражение для изгибающего
момента в сечении
:

4. Составляем приближенное дифференциальное
уравнение упругой линии балки:

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Принимаем жесткость балки постоянной.
Интегрируем дифференциальное уравнение.
Получаем:

.(д)

Постоянную интегрирования
в уравнении (д) найдем из условия, что
приугол поворота в сечении А равен нулю.
Подставим в уравнение (д)и приравняем нулю угол поворота сечения
А. Получим.
Тогда окончательно уравнение для угла
поворота принимает вид:

.(е)

6.
Подставляем в уравнение (е) координату
,
получим угол поворота в сечении С:

7.
Подставляем в уравнение (е) координату
.
Получим угол поворота в сечении В:

8. Сравнивая углы
поворота в сечениях В и С, получим:

Таким образом,
угол поворота в сечении В в 1,016 раза
больше, чем угол поворота в сечении С.

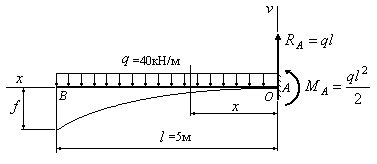
Пример
6.5.
Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна
кНм².

Рис.6.7

Решение:

Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении
:

.
(ж)

Постоянные
интегрирования в уравнении (ж) получим,
воспользовавшись граничными усорвиями
закрепления балки, в соответствии с
которыми прогиб и угол поворота в жесткой
заделке равны нулю:

при
и.

Подставляя
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:;.
Тогда выражение для прогиба принимает
вид:

Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба (),
находим:

ммм.

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.

Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.

Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.

Виды балок

При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.

Виды балок:

Деревянные
— их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
Металлические
— такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.

Определение — стрела — прогиб

Определение стрелы прогиба и предела прочности при сжатии-факультативно, если оно не оговорено ТУ заказа.

Кроме определения стрелы прогиба и напряжений смятия иногда определяют суммарные напряжения сг2, возникающие в распределительном вале от совместного действия изгибающего и скручивающего моментов.

Кроме определения стрелы прогиба и напряжений смятия иногда определяют суммарные напряжения as, возникающие в распределительном вале от совместного действия изгибающего и скручивающего моментов.

Для определения стрелы прогиба лист материала кладут Йогнутой стороной вверх на горизонтальную плоскость. Параллельно краю листа прикладывают линейку с предпочтительной длиной 1000 мм. Масса линейки не должна оказывать влияния на результат измерения. Измеряют максимальное расстояние ( просвет) между линейкой и поверхностью листа.

Для определения стрелы прогиба ремня необходимо приложить к ремню линейку и нажимать большим пальцем на ремень в его средней части с усилием: для двигателей автомобилей ГАЗ и ЗИЛ-3-4, для ЯМЗ — около 10 кгс, установив, таким образом, на сколько миллиметров прогнулся ремень.

Читать также: Простой регулятор тока своими руками

Для определения стрелы прогиба ремня необходимо приложить к ремню линейку и нажать большим пальцем на ремень в его средней части с усилием: для двигателей автомобилей ГАЗ и ЗИЛ — 3 — 4, для ЯМЗ — около 10 кгс, при этом прогиб ремня у двигателей ГАЗ должен быть 12 — 20, у ЗИЛ-120, 121 и ГАЗ-21 — 10 — 15, у ЯМЗ — 13 — 19, у автомобилей ЗИЛ-158, Урал-15 — 20 мм.

При определении стрелы прогиба ступенчатых валов в расчет принимают некоторый усредненный диаметр.

Формула (16.31) для определения стрелы прогиба в середине стержня при внецентренном приложении нагрузки является приближенной, так как изогнутая ось стержня принята в виде полуволны синусоиды.

Контроль изогнутости требует определения стрелы прогиба в продольном сечении изделия при прокручивании его на ножах.

Особенностью расчета этих шеверов является определение стрелы прогиба боковой поверхности зубьев и изменения толщины зуба по длине шевера.

Прочность и жесткость балки

При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.

На эти параметры влияют следующие факторы:

величина наружных нагрузок, их положение;
параметры, характер, нахождение поперечного сечения;
продольные величины;
материал;
число опор, метод их закрепления.

Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.

Расчет на жесткость

Алгоритм исчисления:

В формуле обозначены:

M – max момент, возникающий в брусе;
Wn,min – момент сопротивления сечения (табличный показатель);
Ry – сопротивление на изгиб (расчётный показатель);
γc – показатель условий труда (табличный показатель).

Такой расчет не трудоемок, но для более верного значения требуется следующее:

рабочий план объекта;
определение характеристик балки, характер сечения;
определение max нагрузки, воздействующей на брус;
оценка точки max прогиба;
проверка прочности max изгибающего момента.

Минимальная высота сварных балок по условиям предельных прогибов.

Наименьшаявысота балокhмин определяется жесткостью балки — ее предельным прогибом. Минимальная высота балки находится из формулы прогиба. Для равномерно распределенной по длине балки нагрузки

f = 5/384 (pн + gн)l4/EJб,

где рн и gн являются — временной (с учетом в необходимых случаях динамического коэффициента) и постоянной нормативными нагрузками на 1 м длины балки (без коэффициента перегрузки); l — пролетом балки; EJб — жесткостью балки на изгиб.

Вопрос 40.

Определение толщины стального настила балок по формуле Телояна и по графикам зависимости от погонной нагрузки и предельного прогиба.

Вопрос 41.

Порядок подбора сечений составных балок.

В следующем порядке:

1. Задавшись ориентировочно , находим по табл. 8.1, , определяем , и . Если расчет ведется по прочности. Находим и принимаем, ориентируясь на , стандартный размер из сортамента металла для стенки

2. Если

Расчет на прогиб и его особенности

Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.

При применении соответствующих коэффициентов, придерживаются следующего:

балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
нагрузка консольного типа;
воздействие комплексной нагрузки.

Проверка прогибов стальной балки

Теги: #ЛИРА-САПР #СТК #прогибы

При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:

Информация из справки LIRA SAPR (СправкаПояснения СтальПроверки прогибов):

Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.

В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.

Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.

Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).

В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.

Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).

На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.

Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.

Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.

Пример расчета однопролетной балки

Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.

Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.

Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»

Предельно допустимый L/200=6000/200=30мм

Без задания раскреплений (по абсолютному перемещению узлов балки): ((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%

С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов): ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Ручной ввод расчётной длины балки для расчёта прогибов

В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.

Информация из справки ЛИРА САПР: Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.

Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.

Результаты расчётов прогибов балок

Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм

Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм

Проценты использования по предельному прогибу

Длина балки 6 м: ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Длина балки 4 м: ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%

Расчёт прогибов стрельчатой арки

Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.

При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):

Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)

Результаты определения прогибов в СТК-САПР:

Предельно допустимый L/200=17664/200=88.32 мм

Без задания раскреплений (по абсолютному значению на эпюре прогибов fz): 96.7/17644=1/182 — совпадает с результатом расчёта элемента №2

С заданием раскреплений (по относительному значению на эпюре прогибов fz): (96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4

Без задания раскреплений (по абсолютному значению перемещений узлов): 99.8/17644=1/177 — не совпадает ни с чем

Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.

Расчёт прогибов цилиндрической арки

Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.

Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:

Загружение 1 — постоянное, коэффициент надёжности 1.1; Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;

Вычислим коэффициенты для перехода к нормативным значениям

Загружение 1 Kn=1/1.1=0.91; Загружение 2 Kn=1/1.2*0.35=0.292

Мозаика перемещений узлов цилиндрической арки от РСН2

Предельно допустимый прогиб L/200=18000/200=90 мм

Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.

Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.

Мозаика перемещений узлов в глобальной СК относительно реперного узла

Источник

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
Форма поперечного сечения и другие геометрические характеристики.
Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

электросварка;
заклепки;
болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Определение — стрела — прогиб

Определение стрелы прогиба и предела прочности при сжатии-факультативно, если оно не оговорено ТУ заказа.

Читать также: Сопротивление первичной обмотки трансформатора 220

При определении стрелы прогиба ступенчатых валов в расчет принимают некоторый усредненный диаметр.

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

Простой. При использовании данного метода применяется увеличительный коэффициент.
Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γc представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

Составление расчетной схемы объекта.
Расчет размеров балки и ее сечения.
Вычисление максимальной нагрузки, которая воздействует на балку.
Определение точки приложения максимальной нагрузки.
Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

размеры балки, длину консолей и пролет между ними;
размер и форму поперечного сечения;
особенности нагрузки на конструкцию и точно ее приложения;
материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Из-за чего прогибаются балки

Причины прогибания балок могут быть первичными и вторичными.

Первичные причины

К первичным факторам, из-за которых опорные элементы перекрытий начинают нуждаться в укреплении, относят неправильный расчет их несущей способности. То есть, когда проектировщик не учел длину пролета и расстояние между балками, не соизмерил эти величины с их сечением и предполагаемой нагрузкой. Иными словами, если изначально для устройства перекрытий был использован брус недостаточной высоты и толщины.

Ещё одна причина – использование некачественного материала: с сучками, трещинами, следами гнили. И невыполнение требований по его предварительной обработке антисептиками.

На заметку! Очень часто такие промахи совершают строители, поэтому так важно постоянно следить за выполнением работ, особенно скрытых. В случае с балками и лагами необходимо убедиться в их соответствии проектным требованиям до того, как будет произведено утепление, так как утеплить перекрытие между этажами в частном доме, значит скрыть несущие элементы от визуального осмотра.

Длина пролета, м	Шаг между балками, м
0,6	1
2	100х70	120х80
3	140х90	160х110
4	160х120	200х120
5	160х120	220х160
6	220х140	250х180

Эти значения определены для нагрузки 400 кг/м2 перекрываемой площади, их можно менять только в большую сторону. В идеале для каждого дома все эти параметры определяются индивидуальными расчетами. Например, если проектом предусмотрен утеплитель для межэтажных перекрытий, какой выбрать шаг между лагами, зависит от его ширины.

Вторичные причины

Даже изначально качественные и достаточно мощные балки со временем могут ослабнуть по следующим причинам:

повреждение древесины вследствие старения, воздействия высокой влажности, порчи насекомыми;
увеличение нагрузки на перекрытия, например, при установке тяжелой мебели, оборудования;
превращение нежилого помещения над перекрытиями в жилое: их утепление, звукоизоляция и монтаж напольного покрытия также создают дополнительную нагрузку.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
Варианты нагружения консольного стержня, который закреплен жестко.
Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Читать также: Приспособление для перекопки земли

Источник