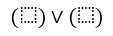Как найти строки в таблице истинности

  1. Определить количество строк и столбцов в таблице истинности.

Т.к. каждое из простых
высказываний может принимать всего два
значения (0 или 1), то количество разных
комбинаций значений n
высказываний – 2 n
 .

Количество строк
в таблице = 2 n
 + строка на
заголовок.

Количество столбцов
в таблице равно сумме количества простых
высказываний (n)
и количества разных логических операций,
входящих в сложное высказывание.

В нашем примере: количество
строк — 22 +
1 = 5 ,

столбцов – 2 + 4 = 6

  1. Начертить таблицу и заполнить заголовок

Первая строка – номера столбцов.

Вторая строка промежуточные формулы и
соответствующие им условные записи
операций над значениями .

  1. Заполнить первые n столбцов.

В нашем примере сначала заполняем 1-й и
2-й столбцы.

  1. Заполнить остальные столбцы.

В соответствии с таблицами истинности
соответствующих логических операций,
причем при заполнении каждого столбца
операции выполняются над значениями
одного или двух столбцов, расположенных
левее заполняемого.

Итак, вычисляем значения 3-го столбца
по значениям 2-го, потом значения 4-го –
по значениям 1-го и 2-го…

К

С

 С

К  C

( К  C
) &  С

( К  C
) &  С 
К

1

1

0

1

0

1

0

1

0

1

0

1

1

0

1

1

1

1

0

0

1

0

0

1

Вывод: получили в последнем столбце все
единицы. Значит, значение сложного
высказывания истинно при любых значениях
простых высказываний К и С. Следовательно,
учитель рассуждал логически правильно.

СДНФ
(Совершенная Дизъюнктивная Нормальная
Форма) —
это такая ДНФ,
которая удовлетворяет трём условиям:

  • в
    ней нет одинаковых элементарных
    конъюнкций

  • в
    каждой конъюнкции нет одинаковых
    пропозициональных букв

  • каждая
    элементарная конъюнкция содержит
    каждую пропозициональную букву из
    входящих в данную ДНФ пропозициональных
    букв, причем в одинаковом порядке.

Для
любой функции алгебры логики существует
своя СДНФ, причем единственная.

СКНФ
(Совершенная Конъюнктивная Нормальная
Форма) —
это такая КНФ,
которая удовлетворяет трём условиям:

  • в
    ней нет одинаковых элементарных
    дизъюнкций

  • в
    каждой дизъюнкции нет одинаковых
    пропозициональных переменных

  • каждая
    элементарная дизъюнкция содержит
    каждую пропозициональную букву из
    входящих в данную КНФ пропозициональных
    букв.

Совершенная
конъюнктивная нормальная форма
(СКНФ):

1) нет двух элементарных дизъюнкций;

2) ни одна элементарная дизъюнкция не
содержит двух одинаковых переменных;

3) ни одна элементарная дизъюнкция не
содержит переменную вместе с ее
инверсией;

4) все дизъюнкции имеют один и тот же
ранг.

Совершенная
дизъюнктивная нормальная форма
(СДНФ)

Алгоритм
образования СКНФ и СДНФ по
таблице истинности

1.
Выделить в таблице истинности все
строки, в которых функция принимает
значения 0.

1.
Выделить в таблице истинности все
строки, в которых функция принимает
значения 1.

2. Для каждого выбранного набора
записать элементарные дизъюнкции,
содержащие переменные:

а) если значение переменной равно 0,
то записывается сама переменная,

б) если
значение переменной равно 1, то
записывается инверсия этой переменной.

2. Для каждого выбранного набора
записать элементарные конъюнкции,
содержащие переменные:

а) если значение переменной равно 0,
то записывается инверсия этой
переменной,

б) если
значение переменной равно 1, то
записывается сама переменная.

3.
Соединить элементарные дизъюнкции
знаком конъюнкции.

3.
Соединить элементарные конъюнкции
знаком дизъюнкции.

Полином
Жегалкина —
многочлен над кольцом ,
то есть полином с
коэффициентами вида 0 и 1, где в качестве
произведения берётся конъюнкция,
а в качестве сложения —исключающее
или.
Полином был предложен
в 1927 году Иваном Жегалкиным в
качестве удобного средства для
представления функций
булевой логики.
В зарубежной литературе представление
в виде полинома Жегалкина обычно
называется алгебраической нормальной
формой (АНФ).

Теорема
Жегалкина —
утверждение о существовании и
единственности представления всякой
булевой функции в виде полинома Жегалкина.

Полином
Жегалкина представляет собой сумму по
модулю два произведений неинвертированных
переменных, а также (если необходимо)
константы 1. Формально полином Жегалкина
можно представить в виде

или
в более формализованном виде как:

Примеры
полиномов Жегалкина:

5.

Аксиомы исчисления
высказываний

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

Правил вывода
в ИВ имеется два. Первое из них, называемое
правилом заключения или modus
ponens
(сокращенно mod
pon)
дает по паре формул Ф и Ф 
Ψ формулу Ψ, или, в функциональных
обозначениях,

R1
(Ф, Ф 
Ψ) = Ψ.

Таким образом, mod
pon
– это функция двух переменных, причем
определенная не всюду, а только для пар
формул, очевидным образом согласованных
друг с другом.

Второе из правил
вывода – это правило подстановки.
Операция подстановки Ψ естественно
определяется для произвольных слов.
Итак, пусть Ф и Ψ – слова в некотором
алфавите А, а x
– буква того же алфавита. Результатом
подстановки слова Ψ вместо буквы х в
слово Ф, обозначаемым Sх
Ψ Ф,
называют слово, получающееся из Ф в
результате замены каждого вхождения в
него буквы х на слово Ψ. Например,

Sлжирофл
леля =
жирофлежирофля.

(Отметим на
всякий случай, что все вхождения символа
х в Ф заменяются на Ψ, так сказать,
“одновременно”: дело в том, что в слове
Ψ тоже могут содержаться вхождения
буквы х, но эти новые вхождения на Ψ уже
не заменяются!)

Пусть теперь Ф и
Ψ – формулы ИВ, а А – некоторая его
переменная. Тогда правило подстановки
r2
 формулируется
так:

r2
(Ф) = SА
Ф.

Очевидно, что это
– “параметрическое” правило; иными
словами, имеется целое семейство правил
подстановки, зависящее от двух параметров,
переменной А и формулы Ψ. Применять
можно любое из них.

Пример формального
вывода в ИВ

Мы построим т.н.
комментированный вывод, указывая справа
в скобках основания, по которым та или
иная формула занимает в нашем выводе
соответствующее место.

Ф1: А 
(В 
А) (акс. А1)

Ф2: (А 
(В 
С)) 
((А 
В) 
(А 
С))) (акс. А2)

Ф3: (А 
(В 
А)) 
((А 
В) 
(А 
А))) (SСА
Ф2)

Ф4: (А 
В) 
(А А)
(r1
(Ф1,
Ф3))

Ф5: (А 
(В 
А)) 
(А
А) (SВВА
Ф4)

Ф6: А 
А (r1
(Ф1,
Ф5))

Согласно
данным определениям, наш вывод является
выводом формулы А А.
Построив этот вывод, мы доказали, что

 ИВ
(А 
А).

Отсюда немедленно
следует, что, какова бы ни была формула

в ИВ,

 ИВ
(Ψ 
Ψ)

(достаточно только
что построенный вывод дополнить еще
одним применением правила подстановки).

Отметим некоторые
свойства выводов (их доказательства
представляются очевидными). Хотя мы
формулируем их в разделе, посвященном
ИВ, они справедливы для любого формального
исчисления.

  1. Всякий вывод
    открывается одной из аксиом.

  2. Начальный отрезок
    всякого вывода является выводом. т.е.,
    если

Ф1,
Ф2,
…, Фк,
…, Фn
 –

вывод, то и

Ф1,
Ф2,
…, Фк
–

тоже вывод.

3. Если

Ф1,
Ф2,
…, Фn,
и Ψ1,
Ψ2,
…, Ψ m
 –

выводы, то и
последовательность

Ф1,
Ф2,
…, Фn,
Ψ1,
Ψ2,
…, Ψm
–

тоже вывод.

4. Свойство 3 говорит,
что, приписав один вывод за другим, мы
получим снова вывод. Это утверждение
можно обобщить: пусть Ф1,
…, Фn
и
1,
…, m
–
выводы;
тогда всякая последовательность

X1,
X2,
…, Xm+n,

для которой из
того, что

Xi
= Фi´,
Xj´
= Фj´,
i
< j,
или

Xi
= Ψi´,
Xj
= Ψj´,
i < j,

следует, что i´
< j´,
сама является выводом.

Формула A называется выводимой из
множества формул Г(следствием
множества формул Г) в данной теории,
если существует последовательность A1,…An формул
такая, что An есть A и
для любого i формула Ai есть
либо аксиома, либо одна из формул
множества Г, либо непосредственное
следствие предыдущих формул
последовательности по одному из правил
вывода. В этом случае последовательность
формул A1,…An называется выводомформулы A из
Г. Формулы множества Г
называются гипотезами (допущениями,
посылками) вывода.

Для
сокращения записи утверждения «A есть
следствие множества формул Г»
употребляется обозначение  .
Если множество Г конечно, Г={B1,…Bn},
то вместо {B1,…Bn}  пишут B1,…Bn.
Если Г- пустое множество (вывод является
доказательством), то пишут ,
что равнозначно утверждению «A есть
теорема».

Правила
вывода можно подразделить на общие
(работающие в любых аксиоматических
теориях) и частные (работающие в теориях
определенного типа). Приведем несколько
общих правил, применяемых для построения
доказательств и выводов в любых теориях.

  1. Правило
    повторения посылки:
    .

  2. Правило
    введения посылки: 
    если ,
    то .

  3. Правило
    удаления посылки:
    если  и ,
    то .

  4. Правило
    силлогизма:
    если  то .

Соседние файлы в предмете Математическая логика и теория алгоритмов

  • #

    07.06.2018375.81 Кб101.doc

  • #
  • #
  • #

    07.06.2018442.68 Кб75.docx

  • #
Источник


Видеоурок: Построение таблиц истинности для логических выражений.

При построении таблиц истинности есть определенная последовательность действий.  

1. Определить количество строк в таблице:

· количество строк
= 2n+1, где n – количество логических переменных.

2. Определить количество столбцов в таблице:

· количество
столбцов = количеству логических переменных + количество логических операций.

3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и
приоритетов (¬, &, V);

·  приоритеты:
( ), ¬, &, V.

4. Заполнить столбцы входных переменных наборами значений.

5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий.

Возьмем для примера логическое выражение: ¬(A&B)

и построим таблицу истинности для этого составного высказывания.

Количество строк: 22+1=5, количество столбцов: 2+2=4.

Далее заполняем варианты исходных высказываний А и В. Теперь заполняем другие столбцы по порядку логических операций. 

А

В

A&B

¬( A&B)

0

0

0

1

0

1

0

0

1

0

0

0

1

1

1

0


Закрепление изученного материала

Разберем следующие выражения.

1)     
В&(АVВ) 

Количество логических переменных: 2. Логических операций: 2.     

Значит, строк в таблице 22+1=5, столбцов 2+2=4. 

A

B

AVB

В&(АVВ) 

0

0

0

0

0

1

1

1

1

0

1

0

1

1

1

1

2) А&(A˅B˅C)                     

Количество логических переменных: 3. Логических операций: 3    

Значит, строк в таблице 23+1=9, столбцов 3+3=6.

А

В

С

A˅B

(A˅B)˅C

А&((A˅B)˅C)

0

0

0

0

0

0

0

0

1

0

1

0

0

1

0

1

1

1

0

1

1

1

1

1

1

0

0

1

1

0

1

0

1

1

1

0

1

1

0

1

1

1

1

1

1

1

1

1

Источник

Построение таблиц истинности

Автор статьи

Екатерина Андреевна Гапонько

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Определение 1

Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.

Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.

Определение 2

Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.

Определение 3

Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

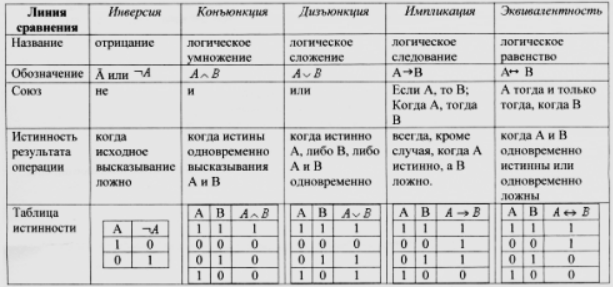
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:

Рисунок 1.

Приоритетом в выполнении порядка выполнения операций пользуются скобки.

Алгоритм построения таблицы истинности логической функции

  1. Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.

  2. Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.

  3. Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.

«Построение таблиц истинности» 👇

Рисунок 2.

Пример 1

Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.

Решение:

  1. Определим количество строк:

    Количество простых выражений – $n=3$, значит

    кол-во строк = $2^3 + 1=9$.

  2. Определим количество столбцов:

    Количество переменных – $3$.

    Количество логических операций и их последовательность:

    1. инверсия ($bar{A}$);
    2. дизъюнкция, т.к. она находится в скобках ($B vee C$);

    3. дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.

      Кол-во столбцов = $3 + 3=6$.

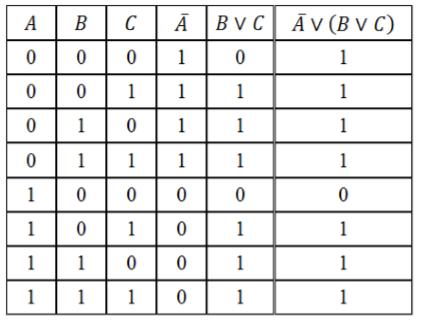
  3. Заполним таблицу, учитывая таблицы истинности логических операций.

Рисунок 3.

Пример 2

По данному логическому выражению построить таблицу истинности:

[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]

Решение:

  1. Определим количество строк:

    Количество простых выражений – $n=3$, значит

    кол-во строк = $2^3 + 1=9$.

  2. Определим количество столбцов:

    Количество переменных – $3$.

    Количество логических операций и их последовательность:

    1. отрицание ($bar{C}$);
    2. дизъюнкция, т.к. она находится в скобках ($A vee B$);
    3. конъюнкция ($(Avee B)bigwedge overline{C}$);
    4. отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
    5. дизъюнкция ($A vee C$);
    6. конъюнкция ($(Avee C)bigwedge B$);
    7. отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);

    8. дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).

      Кол-во столбцов = $3 + 8 = 11$.

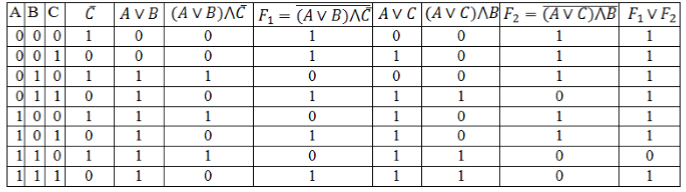
  3. Заполним таблицу, учитывая таблицу истинности логических операций.

Рисунок 4.

Алгоритм построения логической функции по ее таблице истинности

  1. Выделяют в таблице истинности строки со значением функции, равным $1$.
  2. Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
  3. Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
  4. В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.

Пример 3

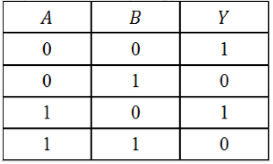
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.

Рисунок 5.

Решение:

  1. Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
  2. Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:

    Рисунок 6.

  3. Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
  4. В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата написания статьи: 12.04.2016

Источник

to continue to Google Sites

Not your computer? Use Guest mode to sign in privately. Learn more

Источник

Построение
таблиц истинности для логических выражений.

ЦЕЛЬ УРОКА:  Формирование у обучающихся навыков
применения технологии построения таблиц истинности для составных логических
выражений.

Задачи урока:

Обучающие:

1.Научить составлять
логические выражения из высказываний

2.Научить находить
значение логических выражений посредством построения таблиц истинности

Развивающие:

1.Продолжить развитие
умения анализировать

2.Формировать умения
работы с таблицами

Воспитательные: 

1.Совершенствовать навыки
общения

2.Вовлечь в активную
деятельность

План урока: 

1.Организационный момент
(1 мин).

2.Повторение материала
предыдущего урока + проверка домашнего задания (устный опрос) (5 мин).

3.Объяснение нового
материала (10 мин).

4.Физкультминутка (1
мин).

5.
Разбор примера для закрепления (3 мин);

6.Задания для самостоятельной работы (10 мин).

7. Домашнее задание (3 мин).

Сегодня мы узнаем, как можно построить таблицу
истинности, которая определяет истинность или ложность логического высказывания
при всех возможных комбинациях исходных значений простых высказываний
(логических переменных).

СЛАЙД
 Правило: При выполнении
логических операций определен следующий порядок:

1.       Инверсия

2.       Конъюнкция

3.       Дизъюнкция

4.       Импликация

5.       Эквивалентность

 Для
изменения указанного порядка выполнения операций используются скобки.

Объяснение нового материала

И
так рассмотрим таблицу истинности на примере и построим ее, по ходу урока будем
записывать правило.

Слайд Для построения таблицы используется
Алгоритм построения таблицы истинности.

Он
состоит из пунктов, но мы их сейчас рассмотрим в процессе составления таблицы
истинности.

1.      Подсчитать
количество переменных n в
логическом выражении;

2.      Определить
количество строк в таблице истинности;

•        
количество
строк  m
=
2n

3.      Подсчитать
количество логических операций в логическом   выражении;

4.      Определить
количество столбцов в таблице, которое равно  количеству логических переменных
плюс количество логических       операций;

5.      Ввести
названия столбцов таблицы в соответствии с последовательностью выполнения
логических операций с учетом скобок и приоритетов;

6.      Заполнить
столбцы входных переменных наборами значений;

7.      Провести
заполнение таблицы истинности по столбцам, выполняя логические операции в
соответствии с установленной последовательностью.

Слайд
( Шаг 1)  определим количество строк в таблице.

Количество
строк высчитывается по формуле:  2n + 1

Где
n – это
количество логических переменных в выражении

+1
– одна строка для шапки таблицы

Далее
посчитаем количество логических переменных,  1 – A, 2 – B, 3 – C.

Итого
3 переменные (A, B, C)

Поэтому
количество строк будет равно 23 + 1 = 9 строк.

Слайд
  (Шаг 2)  Определим количество столбцов в таблице.

Количество
столбцов вычисляется по формуле, количество переменных + количество операций.

Так
как у нас количество переменных 3 (A, B, C)

Посчитаем
количество операций:

Два
отрицания, два умножения (конъюнкция), и одно сложение (дизъюнкция)

Итого
в сумме мы имеем 5 логических операций.

3
логические переменные, + 5 логические операции, = 8 столбцов в нашей таблице.

Построим
таблицу, подпишем столбцы и заполним ее значениями.

Мы
помним, что в таблице будет 9 строк, и 8 столбцов

Подпишем
столбцы, столбцы записываются по следующему правилу:

Сначала
перечисляются все логические переменные, а дальше наши логические переменные, в
последовательности их выполнения.

Надо
запомнить, что сначала выполняется отрицание, далее логическое умножение, потом
логическое сложение.

Если
имеется выражение в скобках, то действие выполняется в скобках, а потом уже
последовательно.

Для
начала расставим последовательность действий

1) ¬B ;                    2) 
¬C;                  3) ¬B /¬C;          4)B / ¬B /¬C;                  5)
А / (B / ¬B /¬C).

Слайд 
(Шаг 3)  Заполним значениями исходных переменных,
есть такое правило:

«
Начиная с последнего записываем 010101»

«Для
второй переменной записываем 00110011»

«Для
третье переменной 0000111100001111»

После
того, как начертили таблицу, заполнили ее значениями исходных переменных,
приступаем к вычислению.

Получили
такую таблицу:

И
дальше смотрим значения таблицы конъюнкции и дизъюнкции и заполняем таблицу по
очереди.

Слайд
 (Шаг 4)  

Закрепление изученного материала

Слайд
9.         Построим таблицу истинности 

Ответ: 

Z =(A / E) / (¬A  / ¬
E)

ДОМАШНЕЕ ЗАДАНИЕ Страница 39  Задание 8

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти устройство по блютуз адресу
  • Как найти кассовый чек по инн организации
  • Как найти объем пирамиды хеопса
  • Как найти фото людей по фотографии
  • Как мне найти телефон дома