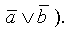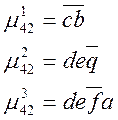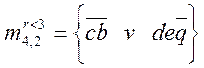Как найти структурную матрицу

1. Структурные матрицы и операции с ними

Для
структурного анализа сетей (нахождения
путей, сечений и их характеристик)
целесообразно использовать структурные
матрицы и некоторые операции, основанные
на применении математического аппарата
булевой алгебры. Каждый путь μ^h_st
(сечение
σ^l_st)
будем
представлять произведением (конъюнкцией)
символов ребер, образующих этот путь
(сечение), а множество путей (сечений) —
дизъюнкцией (логической суммой) этих
произведений.

Так,
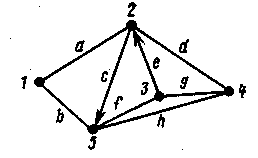
для сети, изображенной на рис. 2, запишем:

;
.

Структурной
матрицей
В
сети G
с N
узлами
будем называть квадратурную матрицу
порядка N,
в
которой каждому узлу а_i,
соответствуют i-я
строка
и i-й
столбец:

.

Здесь
i,
j
= 1, N.
Вхождения
β_ij
определяются по следующему правилу:

Если
все ребра не направлены, то матрица
будет симметричной по отношению к
главной диагонали, а если есть направленные
ребра, то несимметричной. Для сети,
изображенной на рис. 6 структурная
матрица будет иметь вид:

.

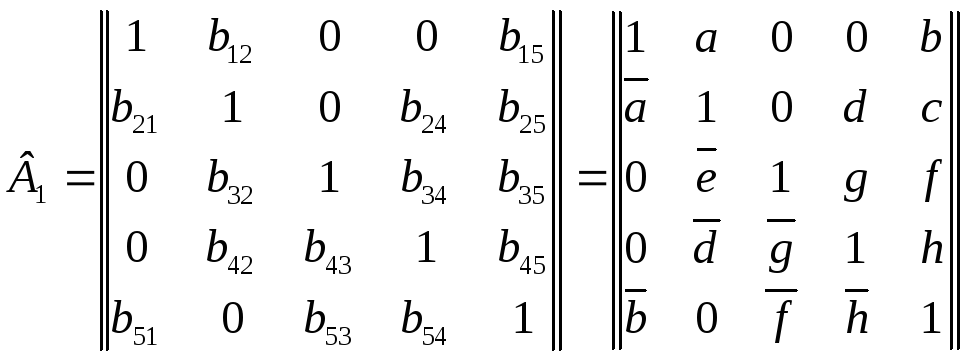
Структурную
матрицу можно рассматривать как булеву
матрицу и применять к ней аппарат булевой
алгебры (алгебры логики); в частности,
может быть применен аппарат преобразования
булевых матриц и булевых определителей.
Не останавливаясь подробно на этом
аппарате, отметим только некоторые
особенности, связанные с интерпретацией
сети булевыми матрицами

Рис.
6.
Пример
сети

В
булевой алгебре, в которой переменные
и функции могут принимать только два
значения (0 и 1), используются три операции:
логическое произведение (конъюнкция,
обычно обозначаемая точкой, которая
может опускаться, а иногда знаком
),
логическое сложение (дизъюнкция, для
которой будем применять символ V,
хотя иногда используется знак +) и
инверсия (черта над переменной или
функцией).

В
отличие от «обычной» алгебры, в булевой
алгебре 1V1
= 1, а отсюда вытекают и некоторые особые
преобразования:

Aa = a; aVa = a; 1a = a;
1Va = 1; a(aVb) = a; aVab = a;

a
= 0; aV
= 1.

Произведение
двух булевых квадратных матриц

и

порядка N
приводит
к квадратной матрице С
= АВ =

того же порядка, вхождения которой γ_ij
равны
сумме (дизъюнкции) почленных произведений
i-й
строки матрицы А
и i-го
столбца матрицы В:

.

При
возведении структурной матрицы в квадрат
получим новую структурную матрицу С
= В²
с единицами по главной диагонали, а ее
вхождения γ²_ij
будут включать в виде суммы как не
посредственное ребро b_ij
(если
оно было в сети), так и все пути ранга 2
(проходящие через один узел) от узла а_i
к
узлу
a_j
вида
b_ilb_lj
(если
они есть в сети).

Так,
при возведении в квадрат матрицы В₁
соответствующей
сети рис. 6, для вхождения γ²₁₅
получим (выписываем первую строку и
пятый столбец и производим перемножение)

1

a

0

0

b

γ215

=

b

c

f

h

1

b

V

ac

V

0

V

0

V

b

=

b

V

ac,

т.е.
от узла 1
к узлу 5
имеются прямое ребро b
и путь ас
ранга 2 (через узел 2). Проведя расчет,
получим следующую матрицу В²₁
путей ранга r
≤ 2:

.

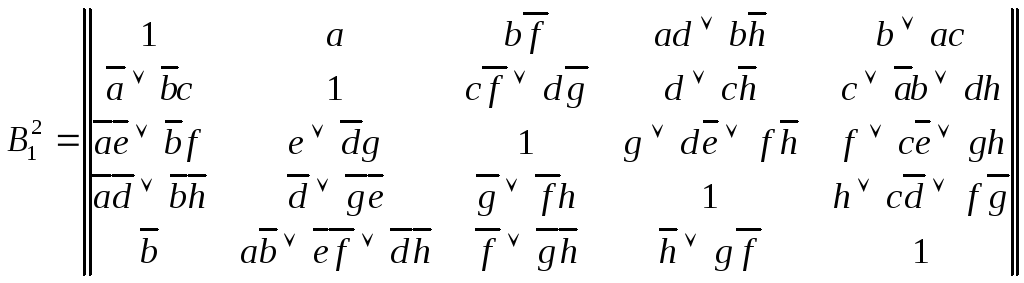
Для
возведения в третью степень перемножаются
матрицы В²
и В.
Так, для определения вхождения γ³₁₄
перемножаем первую строку матрицы В²
и четвертый столбец матрицы В:

Возведение
структурной матрицы в q-ю
степень
приводит к тому, что каждое вхождение
новой матрицы будет содержать все пути
от узла a_i
к
узлу а_j,
ранга
не более q,
т.
е.
.
Имеется некоторое q_max,
такое,
что дальнейшее возведение матрицы в
степень не меняет ее вхождений, т. е.

.

Матрица
М_хар
=

называется характеристической или
матрицей всех путей, содержит все
возможные в сети пути между узлами.
Поскольку максимальный ранг пути не
может превышать N-1,
то q_max
≤ N-1.
Аналогично могут быть составлены матрицы
М*
путей,
обладающих свойством *, для которых
вхождениями будут множества т*_ij.

Остановимся
на некоторых правилах вычисления
определителей (детерминантов) булевых
матриц. Вычисление (раскрытие) таких
определителей производится по методам,
аналогичным методам вычисления
определителей в обычной алгебре, с той
разницей, что все члены, появляющиеся
в процессе вычисления, берутся только
со знаком V
и производятся преобразования, вытекающие
из законов булевой алгебры. Отметим
некоторые особенности булевых
определителей: а) если в определителе
в каждой строке и столбце имеется хотя
бы одна единица, то определитель
тождественно равен 1; б) если в определителе
какой-либо ряд (строка или столбец)
состоит из одних нулей, то определитель
тождественно равен нулю; в) если перед
определителем имеется множитель х,
то
во всех вхождениях определителя х
может
быть заменен единицей, а

—
нулем.

Вычисление
определителей производится разложением
определителя по вхождениям какого-либо
ряда (строки или столбца), что дает
возможность при каждой операции снизить
порядок определителя на единицу. При
этом для уменьшения операций по
«поглощению» лишних слагаемых
рекомендуется раскладывать по ряду, в
котором нет единиц.

Разложение
определителя матрицы А
ранга N
с
вхождениями a_ij
по i-й
строке будет иметь вид:

,

где
|A_jj|-определитель
матрицы дополнения, полученной из
матрицы А
вычеркиванием i-й
строки и j-го
столбца.

Для
определителей третьего и второго порядка
можно применить обычную процедуру
раскрытия по диагонали, считая b_ijb_ji
= 0
или
a
= 0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

24.2 Матрицы и графы. Нахождение путей и сечений
с помощью структурной матрицы

Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.

1. Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности a_ij равен 1, если эти вершины связаны s ребрами, то а_ij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.

Легко видеть, что матрица В =А² = АА составлена из целых чисел b_ij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А³ составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину j и т. д.

1. Матрица инциденций – это матрица размера n´ m, где n – число вершин, а m – число ребер графа, при этом ее элементы k_ij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
2. Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. a_ii = 1, остальные элементы  – это символьные обозначения ребер (если вершины i и j не соединены ребром, то a_ii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент s_ij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aÚ b, а при i>j этот элемент равен

Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.

Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.

Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.

Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ú a = 1, (это свойство нужно, для того чтобы не проходить по одному ребру дважды в противоположных направлениях), а также используется правило простого поглощения (хÚ ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.

Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.

2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).

Сечением (разрезом) между вершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.

Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.

Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить.

Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.

1. Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности a_ij равен 1, если эти вершины связаны s ребрами, то а_ij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.

   Легко видеть, что матрица В =А² = АА составлена из целых чисел b_ij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А³ составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину jи т. д.

2. Матрица инциденций – это матрица размера nґ m, где n – число вершин, а m – число ребер графа, при этом ее элементы k_ij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
3. Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. a_ii = 1, остальные элементы  – это символьные обозначения ребер (если вершины i и j не соединены ребром, то a_ii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент s_ij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aЪ b, а при i>j этот элемент равен 

Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.

Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.

Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.

Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ъ a = 1, 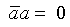(это свойство нужно, для того чтобы не проходить по одному ребру дважды в противоположных направлениях), а также используется правило простого поглощения (хЪ ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.

Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.

2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).

Сечением (разрезом) между вершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.

Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.

Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то всесечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить. Пример на эту тему приведен в разд. 15 (примеры решения типовых задач).

Министерство связи РФ

Сибирский Государственный университет

телекоммуникаций и информатики

 Контрольная работа по курсу:

Сети связи

студента группы ЗТ-03

                                                                                 заочного
факультета АЭС

                                                                                 А.
С. Сидоров

Новосибирск – 2002 г.

Вариант №36

                 Задача  1:             Провести 
анализ  сети,  схема  которой  дана  на  рис. 1:

1.  Найти 
структурную  матрицу  сети

2.  Найти 
все  возможные  пути  от  узла  коммутации  УК_i 
до  УК_j . Номера  узлов  i
– 4,  j – 2,  в  соответствии  с  номером  варианта  0.

3.  Определить 
пути  ранга  r  не  более  трех  для  заданной  в  п.
2  пары  УК_i — УК_j.

4.  По 
заданной  матрице  построить  дерево  путей  ранга  r 
на  более  3  между  УК_i  и  всеми  другими 
узлами  сети.  Выделить  в  дереве  путей  пути  с  r < 3 
для  связи  с  углом  j  и  сравнить  полученный 
результат  с  результатом  п.  1  задания.

5.  Найти 
квазисечения  между  УК_i  и  УК_j  для  множества  путей  r < 3.

6.  Определить  
вероятность  связности  узлов  коммутации  сети  связи  УК_i  и  УК_j
 — ,  если  определено  множество 
путей,  которые  могут  быть  использованы  для  связи  между  указанными  УК. 
Ограничить  ранг  путей  r < 3.  Решение  провести 
для  данных,  указанных  в  п.  2,  используя  результат  решения  п.  3. 
Определить  численное  значение  ,  при  условии,  что 
вероятности  безотказной  работы  ребер  сети  одинаковы  и  равны  0.9.

                 Решение:   Граф 
на  рис. 1  содержит  6  вершин  (УК)  и  9  ребер  (пучков  каналов), 
обозначенных  для  кратности  буквами.  Ранг  вершины  (число  ребер, 
опирающихся  на  данную  вершину)  в  нашем  случае  не  превышает  4  (4,  2). 
Запишем  пути  от  узла  4  к  УК 2:

Совокупность  путей  от  УК4  к 
УК₂  можно  записать:

Из  m_4,2 
можно  выделить  множество  путей,   ранг  которых  будет  не  более  r < 3:

Для  анализа  сети,  т.е. 
нахождения  путей  и  сечений,  используют  структурную  матрицу  В.  В –
квадратная  матрица,  строки  и  столбцы  которой  сопоставлены  с  узлами 
сети.  Связь  внутри  узла  отображается  единицей,  если   связи  между 
узлами  нет,  то  элемент  равен  0.

Определим  из  из  матрицы  В  m₄₂  и  проведем  разложение  по  ненулевым 
членам  четвертой  строки  и  далее:

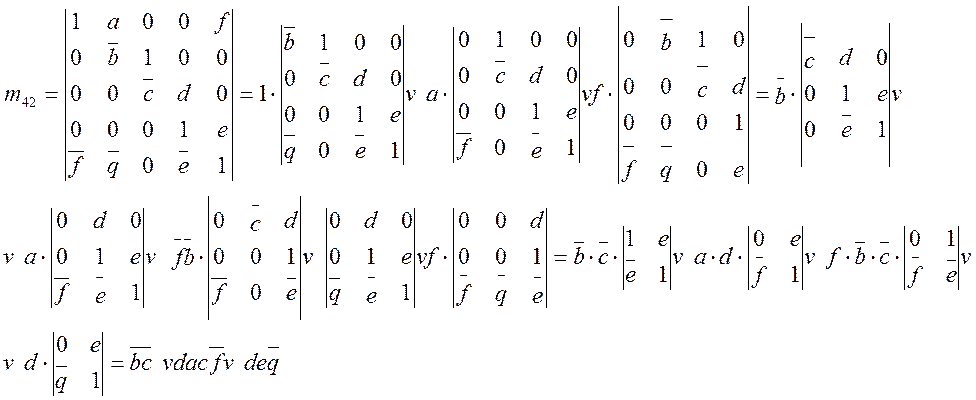
 Графический  эквивалент 
перечня  путей – дерево  путей – можно  построить  непосредственно  по  матрице 
В.  Для  построения  дерева  путей  из  УК4  берем  4  строку  матрицы  В  и 
помечаем  на  графе  вершины  путей  с  r = 1, 
имеющие  b_ij ¹ 0.  После  того,  как  процесс  для 
строки  закончен  и  отмечены  номера  узлов  (по  номеру  столбца),    переходим 
к  строке  одного  из  тех  узлов,     который  расположен  на  линии  r = 1,  и  продолжаем  процесс  аналогичным  образом.  При 
этом  следует  учитывать,  что  узлы  в  одном  пути  не  должны  повторятся.  
Дерево  путей  для  УК₄  (r
< 3)  показано  на  рис.  2.