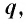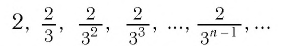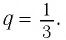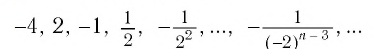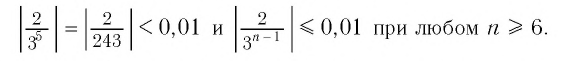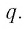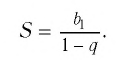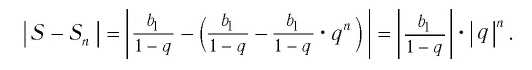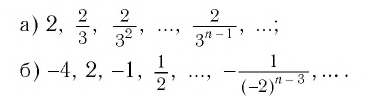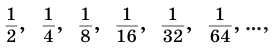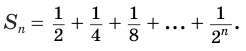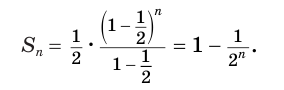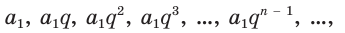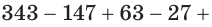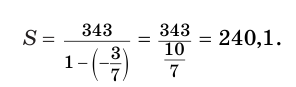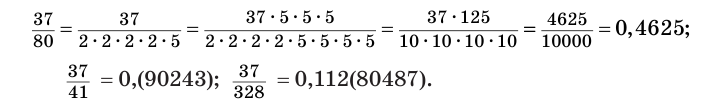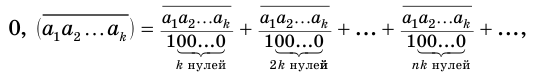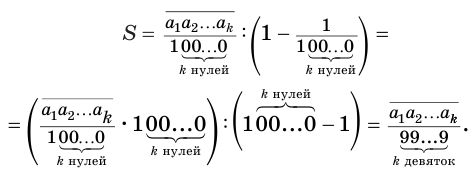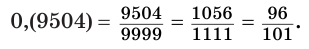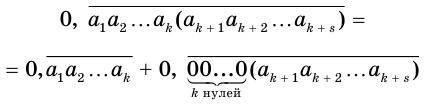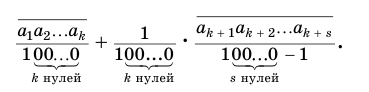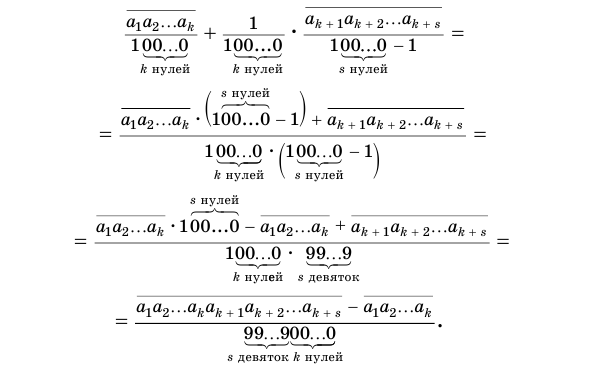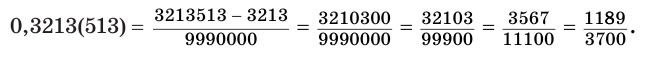Формулы для нахождения суммы бесконечной геометрической прогрессии
Содержание:
- Что такое геометрическая прогрессия
- Бесконечная убывающая геометрическая прогрессия — что из себя представляет
- Сумма первых n членов геометрической прогрессии
- Как найти q в геометрической прогрессии
- Примеры решения задач
Что такое геометрическая прогрессия
Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число (Xn), то говорят, что представлена числовая последовательность. Она имеет вид: (X_1, X_2)
,…,(X_n), или ({[X_n]}). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности (f(n)=X_n.)
Геометрическая прогрессия — последовательность с заданным первым членом (b_1), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число (q).
Числа ( b_1) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:
(b_n=b_{n-1}cdot q,)
Где (b_n) — (n-й) член прогрессии, (q) — знаменатель прогрессии.
Геометрическая прогрессия может быть задана рекуррентным соотношением:
(b_1=b,) (b_{n+1}=b_ncdot q,) (nin N,) (bneq0), (qneq0.)
Примечание
Рекуррентное соотношение задается формулой, выражающей (Xn) через предшествующие ему члены последовательности.
Примеры геометрических прогрессий:
- 1, 2, 4, 8, 16, 32 …; (b_1 = 1), (q = 2;)
- 1, 3, 9, 27, 81…; (b_1 = 1), (q = 3;)
- 2, -8, 32, -128, 512…:(b_1 = 2), (q = -4.)
Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:
(left|b_nright|=sqrt{b_{n-1}cdot b_{n+1}},) (ngeq2, )
или
(b_n^2=b_{n-1}cdot b_{n+1}.)
Если (b_1 > 0) и (q > 1) или (b_1 < 0) и (0 < q < 1), то для геометрической последовательности характерно возрастание.
Если (b_1 > 0) и 0 < (q < 1) или (b_1 < 0) и (q > 1), то для нее характерно убывание.
Примеры геометрических прогрессий в жизни:
- Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
- Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
- Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
- Начисление процентов по вкладу в банках может осуществляться по простой или сложной схеме: соответственно, проценты начисляются либо по арифметической, либо по геометрической прогрессиям.
Бесконечная убывающая геометрическая прогрессия — что из себя представляет
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы (|q| <1.)
Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:
(S=frac{b_1}{1-q}.)
Доказательством этой формулы является то, что величина (q^n) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.
Пример такой прогрессии:
1, (frac12,) (frac14,) (frac18), (frac1{16},…)
Если (q=1), то для вычисления суммы (S_n) первых n членов геометрической прогрессии применяют следующую формулу:
(S_n=b_1+…+b_n=frac{b_1-b_nq}{1-q}=frac{b_1left(1-q^nright)}{1-q}.)
Если (q≠1), то формула видоизменяется в:
(S_n=b_1n.)
Также для объяснения формулы, введем другое обозначение суммы первых членов прогрессии:
(S_n=b_1+b_2+…+b_n.)
Тогда можно видоизменить формулу нахождения суммы (S_n) первых n членов геометрической прогрессии:
(S_n=b_1frac{q^n-1}{q-1}.)
Как найти q в геометрической прогрессии
Вычисление знаменателя прогрессии (q) осуществляют через выведение из формулы на нахождение общего члена геометрической прогрессии:
(b_n=b_1q^{n-1} )
Отсюда:
(q=frac{b_{n+1}}{b_n}.)
Примеры решения задач
Задача № 1
Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.
Найти знаменатель и первый член геометрической прогрессии.
Решение:
По условиям задачи:
(b_1+b_1q^2=35.,)
(b_1left(1+q+q^2+q^3+q^4right)=49left(frac1{b_1}+frac1{b_1q}+frac1{b_1q^2}+frac1{b_1q^3}+frac1{b_1q^4}right).) (2)
Так как (1+q+q^2+q^3+q^4neq0) (иначе задача теряет смысл), то равенство (2) можно записать в виде:
(b_1^2q^4=49. ) (3)
Из (3) следует, что либо (b_1q^2=7,) либо (b_1q^2=-7.)
Если равно 7, то из (1) находим (b_1=28,) (q^2={textstylefrac14}), откуда (q=pmfrac12 )
Если равно -7, (b_1=42,) (\q^2=-{textstylefrac16}). В этом случае второе условие задачи теряет смысл.
Конечный результат:
(b_1=28,) (q=pmfrac12. )
Задача № 2
(S_n) — сумма первых n членов геометрической прогрессии.
Доказать, что: (S_nleft(S_{3n}-S_{2n}right)=left(S_{2n}-S_nright)^2). (1)
Доказательство:
Пусть (b_k — k-й) член, (q)— знаменатель геометрической прогрессии. Тогда:
(S_{m+k}=S_m+b_1q^m+b_1q^{m+1}+…+b_1q^{m+k-1},)
откуда:
(S_{m+k}-S_m=q^mleft(b_1+b_1q+…+b_1q^{k-1}right))
или
(S_{m+k}-S_m=q^mS_k) (2).
Полагая в (2) сначала (m = 2_n,) (k = n), а затем (m = n), (k = n), получаем
(S_{3n}-S_{2n}=q^{2n}cdot S_n), (S_{2n}-S_n=q^ncdot S_n.) (3)
А из равенств (3) следует равенство (1).
Задача № 3
Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.
Найти первый член и знаменатель этой прогрессии.
Решение:
Обозначим: (b_1) — первый член, (S) — сумма прогрессии, (q) — знаменатель, (S_1) — сумма возведенных в третью степень ее членов.
Тогда
(S=frac{b_1}{1-q}),( S_1=frac{b_1^3}{1-q^3}.)
Далее получаем
(frac{S^3}{S_1}-frac{1-q^3}{{(1-q)}^3}=frac{4^3}{192}=frac13 )
(3(1+q+q^2)=1-2q+q^2,;qneq1..)
Полученное уравнение, записанное в виде
(2q^2+5q+2=0)
имеет корни (q_1 = −2,) (q_2 = − ½.)
Так как (|q| < 1), отбрасываем первый корень.
Следовательно:
(q=-frac12,;b_1=4(1-q)=6.)
Задача № 4
(S_n)первых трех членов геометрической прогрессии равна 351. (S_n) следующих трех членов равна 13.
Найти первый член и знаменатель прогрессии.
Решение:
Запишем условия задачи в виде системы уравнений:
(left{begin{array}{l}b_1+b_2+b_3=351,\b_4+b_5+b_6=13end{array}right.Leftrightarrow left{begin{array}{l}b_1+b_1q+b_1q^2=351,\b_1q^3+b_1q^4+b_1q^5=13end{array}right.Leftrightarrow left{begin{array}{l}b_1(1+frac13+frac19)=351,\q=frac13end{array}right.Leftrightarrowleft{begin{array}{l}frac{13}9b_1=351,\q=frac13end{array}Leftrightarrowleft{begin{array}{l}b_1=frac{351cdot9}{13}=243,\q=frac13.end{array}right.right..)
Ответ: (b_1=243,;q=frac13.)
Задача № 5
Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.
Найти знаменатель прогрессии?
Решение:
Определим, что в прогрессии 2n членов и (S_{2n}) — сумма всех членов, а (S_n^ast) — сумма членов, стоящих на нечетных местах.
Тогда (S_{2n}=frac{b_1(1-q^{2n})}{1-q}.)
И
(S_n^ast=b_1+b_3+…+b_{2n-1}=b_1+b_1q^2+…+b_1q^{2n-2}=frac{b_1(1-q^{2n)}}{1-q^2}.)
Где (b_1) — первый член прогрессии, а (q ≠ 1) — знаменатель прогрессии.
По условию задачи:
(S_{2n}=3S_n^astRightarrowfrac{b_1(1-q^{2n)}}{`1-q}=3frac{b_1(1-q^{2n)}}{1-q^2}Rightarrow1+q=3Rightarrow q=2.)
Ответ: (q=2. )
Содержание:
Определение:
Геометрическая прогрессия со знаменателем
Примеры бесконечно убывающих геометрических прогрессий
Приведем примеры бесконечно убывающих геометрических прогрессий.
Пример №1
Последовательность
является бесконечно убывающей геометрической прогрессией с
первым членом 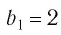
Пример №2
Последовательность
является бесконечно убывающей геометрической прогрессией с первым членом 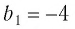
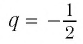
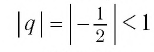
Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением 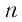
Например, если мы зададим число 0,01, то
Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).
И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.
Например, если мы зададим число 0,001, то 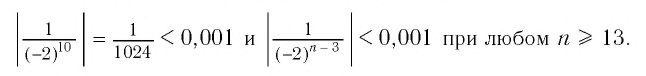
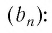
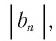
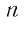
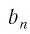
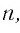
Заметим, что если 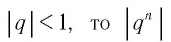
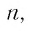
Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членом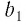
Запишем формулу суммы первых 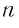
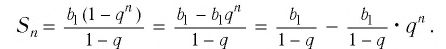
Тогда получим
Так как 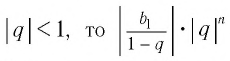
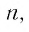
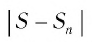
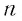
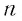
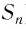
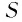
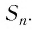
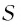
Пример №3
Найти сумму бесконечно убывающей геометрической прогрессии:
Решение:
Ответ:
- Заказать решение задач по высшей математике
Всё о бесконечно убывающей геометрической прогрессии
Пример:
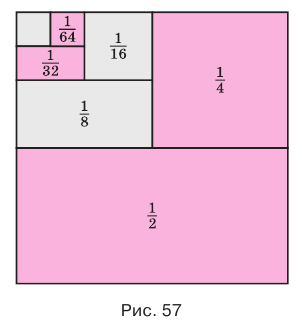
Рассмотрим квадрат со стороной 1 (рис. 57). Если середины его противоположных сторон соединить отрезком, то возникнут два прямоугольника с площадью 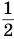
Если теперь середины одного из полученных прямоугольников соединить отрезком, то получится два прямоугольника с площадью 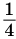
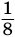
у которой каждый следующий член получается из предыдущего умножением на 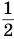
Естественно считать, что сумма 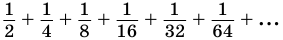
Записанная сумма содержит бесконечно много слагаемых. Рассмотрим ее часть 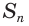
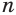
Ее компоненты образуют геометрическую прогрессию со знаменателем 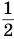
С возрастанием значения переменной 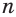
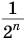
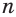
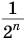
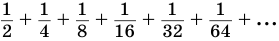
Рассмотрим теперь бесконечную геометрическую прогрессию
где 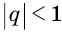
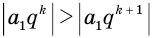
Сумма бесконечно убывающей геометрической прогрессии
Суммой членов бесконечно убывающей геометрической прогрессии 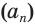
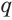
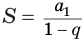
Это определение объясняется тем, что с увеличением 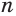
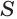
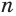
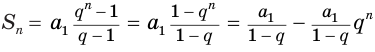
Поскольку 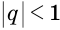
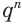
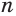
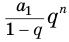
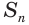
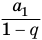
Пример №4
Найдем значение суммы
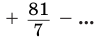
Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой 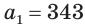
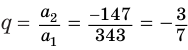
Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:
Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.
Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.
В дальнейшем мы будем пользоваться записью вида 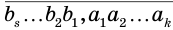
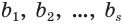
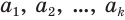
Теорема 7.
Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.
Доказательство:
Пусть 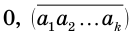
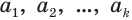
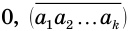
в которой каждое слагаемое получается из предыдущего умножением на 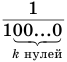
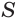
членом 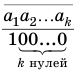
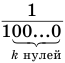
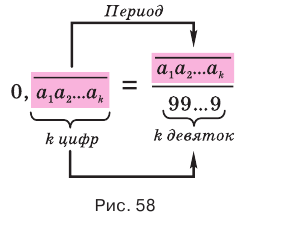
Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.
Пример №5
Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:
Теорема 8.
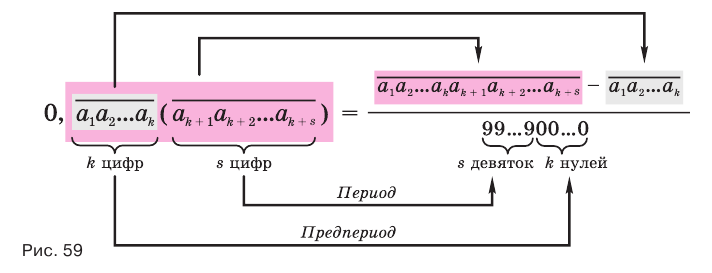
Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.
Доказательство:
Пусть 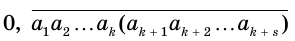
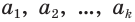
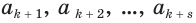
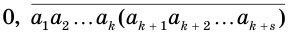
или, с учетом теоремы 7, суммой
Преобразуем полученное выражение:
Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом, который отражен на схеме, представленной на рисунке 59.
Пример №5
Представим обыкновенной дробью десятичную дробь 0,3213(513). Имеем:
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем
- Логарифм — формулы, свойства и примеры
- Корень n-й степени
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
Теория вопроса
Геометрическая прогрессия – это бесконечная последовательность чисел, записанная в виде: b1, b2, …, bn, …, где b1 — первый член, b2 — второй член, bn — «энный» член прогрессии.
Каждый член этой прогрессии, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число «q» ,
Число «q» называется знаменателем прогрессии.
Любой член геометрической прогрессии вычисляется по формуле:
bn = b1 q n — 1 .
Сумма «n» первых членов геометрической прогрессии вычисляется как:
Интерес также представляет «Бесконечно убывающая геометрическая прогрессия». Это геометрическая прогрессия, у которой | q | < 1 . Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии, а именно: это число «к», которому неограниченно приближается сумма «n» первых членов рассматриваемой прогрессии при неограниченном возрастании числа «n».
Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:
Приведем примеры задач, где необходимо использовать эти формулы.
Пример 1
Найти девятый член (b(9)) заданной последовательности чисел: 1, 3, 9, 27, …
Решение
Данная последовательность чисел является геометрической, так как при делении каждого её члена на предыдущий получается одно и то же число «3»:
3 : 1 = 3
9 : 3 = 3
27 : 9 = 3
Следовательно, знаменателем рассматриваемой последовательности является число q = 3.
Применим формулу для нахождения суммы «n» первых членов геометрической прогрессии и найдем b(9):
bn = b1 q n — 1
b9 = 1 х 3 9 — 1 = 1 х 3 8 = 1 х 6561 = 6561
Пример 2
Найти сумму членов бесконечно убывающей геометрической прогрессии:
Решение
Применим формулу для вычисления суммы бесконечно убывающей геометрической прогрессии. В нашем примере b1 = 1, q = 1/2.
Тогда:
Как видите, без знания формул найти требуемые элементы геометрической последовательности не представляется возможным.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Сумма бесконечно убывающей прогрессии, формула.
Сумма бесконечно убывающей прогрессии это число, к которому
неограниченно приближается сумма первых n членов убывающей прогрессии при неограниченном возрастании числа n.
Сумма бесконечно убывающей прогрессии выражается формулой:
[s = frac{a_1}{1 — q}]
(a1 — первый член прогрессии; q — знаменатель прогрессии;)
Вычислить, найти сумму бесконечно убывающей прогрессии по формуле (1).
| a1 | q |
Вычислить
нажмите кнопку для расчета
Сумма бесконечно убывающей прогрессии |
стр. 84 |
|---|
Сходящиеся последовательности. Бесконечно убывающая геометрическая прогрессия
- Предел последовательности
- Свойства сходящихся последовательностей
- Сумма бесконечно убывающей геометрической прогрессии
- Примеры
п.1. Предел последовательности
Рассмотрим последовательность с $a_n$ = $frac{3n + 1}{n + 1}$ Выделим целую часть у дроби: $$ mathrm{ a_n=frac{(3n+3)-2}{n+1}=frac{3(n+1)}{n+1}-frac{2}{n+1}=3-frac{2}{n+1} } $$ Заполним таблицу:
$$ mathrm{ a_n } $$
$$ mathrm{ 3-frac{2}{2}=2 } $$
begin{gather*} mathrm{ 3-frac{2}{11}=}\ mathrm{=2frac{9}{11} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{101}=}\ mathrm{=2frac{99}{101} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{1001}=}\ mathrm{=2frac{999}{1001} } end{gather*}
begin{gather*} mathrm{ 3-frac{2}{10001}=}\ mathrm{=2frac{9999}{10001} } end{gather*}
Чем больше n, тем ближе an к 3.
Этот факт записывают следующим образом: $$ mathrm{ lim_{{n}rightarrowinfty}a_n=lim_{{n}rightarrowinfty}frac{3n+1}{n+1}=3 } $$ и говорят, что число 3 является пределом последовательности {an}.
Число (mathrm{binmathbb{R}}) называют пределом последовательности {an}, если последовательность {an – b} является бесконечно малой, т.е. все её элементы, начиная с некоторого, меньше по модулю любого заранее взятого положительного числа: $$ mathrm{ lim_{{n}rightarrowinfty}a_n=bLeftrightarrow forallvarepsilon gt 0 exists N_{varepsilon}inmathbb{N}: ngeq NRightarrow |a_n-b|lt varepsilon } $$
Раскроем модуль из определения: $$ mathrm{ |a_n-b|lt varepsilon Rightarrow -varepsilon lt a_n-bltvarepsilon Rightarrow b-varepsilonlt a_nlt b-varepsilon } $$ Т.е., начиная с некоторого индекса n, все члены последовательности an (бесконечное множество) попадают в интервал (b – ε; b + ε) – этот промежуток называют ε–окрестностью точки b. Вне этого промежутка находится только первые {a1, a2, …, aN} членов последовательности.
Последовательность, имеющая предел, называется сходящейся.
Последовательность, не имеющая предела, называется расходящейся.
Если предел последовательности (mathrm{ lim_{{n}rightarrowinfty}a_n=0}) последовательность называется бесконечно малой.
Например:
1. Последовательность {an} c (mathrm{ a_n=frac{4n}{n+2}=frac{4(n+2)-8}{n+2}=4-frac{8}{n+2}}) имеет предел (mathrm{ lim_{{n}rightarrowinfty}a_n=4}), значит, является сходящейся.
2. Последовательность {an} c (mathrm{ a_n=4n+2}) при (mathrm{ nrightarrow infty}) также стремится к бесконечности. Предела нет, последовательность расходящаяся.
3. Последовательность {an} c (mathrm{ a_n=frac{1}{n}}) имеет предел (mathrm{ lim_{{n}rightarrowinfty}frac{1}{n}=0}), т.е. является бесконечно малой.
п.2. Свойства сходящихся последовательностей
Свойство 1. Если последовательность имеет предел, то он – единственный.
Свойство 2. Если последовательность имеет предел, то она – ограничена.
Свойство 3. Если все члены последовательности равны a_n=b, то её предел равен b.
Свойство 4. Предел суммы двух последовательностей равен сумме пределов: $$ mathrm{ lim_{{n}rightarrowinfty}(a_n+b_n)=lim_{{n}rightarrowinfty}a_n+lim_{{n}rightarrowinfty}b_n } $$ Свойство 5. Предел произведения двух последовательностей равен произведению пределов: $$ mathrm{ lim_{{n}rightarrowinfty}(a_ncdot b_n)=lim_{{n}rightarrowinfty}a_ncdot lim_{{n}rightarrowinfty}b_n } $$ Свойство 6. Предел частного двух последовательностей равен частному пределов: $$ mathrm{ lim_{{n}rightarrowinfty}left(frac{a_n}{b_n}right)=frac{lim_{{n}rightarrowinfty}a_n}{lim_{{n}rightarrowinfty}b_n} } $$
п.3. Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию с (mathrm{b_1=1, q=frac12}).
Сумма её первых n членов (см.§27 данного справочника) равна: $$ mathrm{ S_n=b_1frac{1-q^n}{1-q}=1cdotfrac{1-frac{1}{2^n}}{1-frac12}=2left(1-frac{1}{2^n}right)=2-frac{1}{2^{n-1}} } $$ Чем больше будет n, тем меньше будет второе слагаемое (mathrm{frac{1}{2^n-1}}). В пределе (mathrm{ lim_{{n}rightarrowinfty}frac{1}{2^{n-1}}=0, lim_{{n}rightarrowinfty}S_n=2}). Удивительно, но мы нашли сумму бесконечного количества слагаемых; и эта сумма конечна.
Обобщим результат для любого |q| < 1: $$ mathrm{ S=lim_{{n}rightarrowinfty}S_n=lim_{{n}rightarrowinfty}left(b_1frac{1-q^n}{1-q}right)=frac{b_1}{1-q}cdot lim_{{n}rightarrowinfty}left(1-underbrace{q^n}_{rightarrow 0}right)=frac{b_1}{1-q} } $$
Бесконечную геометрическую прогрессию со знаменателем |q| < 1 называют бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогрессии конечна и равна: $$ mathrm{ S=frac{b_1}{1-q} } $$
Например:
Представим периодическую десятичную дробь 0,(16) в виде обыкновенной.
Данную дробь можно записать в виде суммы
0,16161616… = 0,16 + 0,0016 + 0,000016 + …=
= 0,16 + 0,16 · 0,01 + 16 · 0,012+…
Это – сумма бесконечно убывающей геометрической прогрессии с b1 = 0,16, q = 0,01, она равна: (mathrm{S=frac{0,16}{1-0,01}=frac{0,16}{0,99}=frac{16}{99}}), т.е.
(mathrm{0,(16)=frac{16}{99}})
п.4. Примеры
Пример 1. Запишите число в виде обыкновенной дроби:
а) 2,(3) begin{gather*} mathrm{ 2,(3)=2+(0,3+0,03+0,003+…)=2+(0,3+0,3cdot 0,1+0,3cdot 0,1^2+…) }\ mathrm{ b_1=0,3, q=0,1 }\ mathrm{ S=frac{b_1}{1-q}=frac{0,3}{1-0,1}=frac{0,3}{0,9}=frac13, 2,(3)=2+frac13=2frac13 } end{gather*}
б) 5,(17) begin{gather*} mathrm{ 5,(17)=5+(0,17+0,0017+0,000017+…)= }\ mathrm{ =5+(0,17+0,17cdot 0,01+0,17cdot 0,01^2+…) }\ mathrm{ b_1=0,17, q=0,01 }\ mathrm{ S=frac{b_1}{1-q}=frac{0,17}{1-0,01}=frac{0,17}{0,99}=frac{17}{99}, 5,(17)=5+frac{17}{99}=5frac{17}{99} } end{gather*}
Пример 2. Найдите сумму бесконечно убывающей геометрической прогрессии:
a) (mathrm{1, frac{1}{sqrt{2}}, frac12,…})
(mathrm{b_1=1, q=frac{1}{sqrt{2}}}) begin{gather*}mathrm{ S=frac{b_1}{1-q}=frac{1}{frac{1}{sqrt{2}}}=frac{sqrt{2}}{sqrt{2}-1}=frac{sqrt{2}(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)}=frac{2+sqrt{2}}{2-1}=2+sqrt{2} } end{gather*}
б) 1, π – 3, (π – 3)2, …
b1 = 1, q = π – 3 begin{gather*} mathrm{ S=frac{b_1}{1-q}=frac{1}{1-(pi-3)}=frac{1}{4-pi} } end{gather*}
Пример 3. Решите уравнение begin{gather*} mathrm{ 1+2x+x^2-x^3+x^4-x^5+…=frac{13}{6}, text{если} |x|lt 1 } end{gather*} Выделим геометрическую прогрессию: begin{gather*} mathrm{ 3x+(1-x+x^2-x^3+x^4-x^5+…)=frac{13}{6} }\ mathrm{ b_1=1, q=-x, S=frac{b_1}{1-q}=frac{1}{1+x} } end{gather*} Получаем: begin{gather*} mathrm{ 3x+frac{1}{1+x}=frac{13}{6}Rightarrow frac{3x(1+x)+1}{1+x}=frac{13}{6}Rightarrow 6(3x^2+3x+1)=13(1+x)Rightarrow }\ mathrm{ Rightarrow 18x^2+5x-7=0 }\ mathrm{ D=5^2-4cdot 18cdot (-7)=25+504=529=23^2, x=frac{-5pm 23}{36}= left[ begin{array}{ l } mathrm{x_1=-frac79} & \ mathrm{x_2=frac12} & end{array}right. } end{gather*} Оба ответа удовлетворяют ограничению |x| < 1.
Ответ: (mathrm{x_1=-frac79; x_2=frac12})
Пример 4. В квадрат со стороной a вписан второй квадрат так, что его вершины являются серединами сторон первого квадрата. А во второй квадрат точно так же вписан третий квадрат, и т.д. Найдите 1) сумму периметров всех квадратов; 2) сумму площадей всех квадратов.
Сторона первого квадрата b1 = a. Сторона второго квадрата равна половине диагонали первого квадрата (mathrm{b_2=frac{1sqrt{2}}{2}=frac{a}{sqrt{2}}}). Сторона третьего квадрата равна половине стороны первого квадрата (mathrm{b_3=frac{a}{2}}), и т.д.
Получаем геометрическую прогрессию со знаменателем (mathrm{q=frac{1}{sqrt{2}}}).
Периметры квадратов линейно зависят от длин сторон: $$ mathrm{ p_1=4a, p_2=4cdotfrac{a}{sqrt{2}}=2sqrt{2}a, p_3=4cdotfrac{a}{2}=2a,… } $$ Для геометрической прогрессии периметров знаменатель будет тем же: (mathrm{q=frac{1}{sqrt{2}}}).
$$ mathrm{ S_p=frac{p_1}{1-q}=frac{4a}{1-frac{1}{sqrt{2}}}=frac{4sqrt{2}a}{sqrt{2}-1}=frac{4sqrt{2}a(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)}=frac{4a(2+sqrt{2})}{2-1}=4a(2+sqrt{2}) } $$ Площади квадратов имеют квадратичную зависимость от длин сторон: $$ mathrm{ s_1=a^2, s_2=left(frac{a}{sqrt{2}}right)^2=frac{a^2}{2}, s_3=left(frac{a}{2}right)^2=frac{a^2}{4},… } $$ Для геометрической прогрессии площадей знаменатель будет равен квадрату знаменателя для прогрессии сторон: (mathrm{q_s=q^2=left(frac{1}{sqrt{2}}right)^2=frac12}).
Сумма всех площадей: begin{gather*} mathrm{ S_s=frac{s_1}{1-q_s}=frac{a^2}{1-frac12}=2a^2} end{gather*} Интересно, что сумма площадей всех(!) квадратов внутри самого большого равна площади этого самого большого квадрата.
Ответ: (mathrm{S_p=4a(2+sqrt{2}), S_s=2a^2})
Пример 5*. В окружность радиуса r вписан правильный треугольник, в треугольник вписана другая окружность, в которую снова вписан правильный треугольник, и т.д. Найдите сумму периметров всех треугольников и сумму длин всех окружностей. 
Сторона правильного треугольника, вписанного в первую окружность: (mathrm{a_1=2rcdot sin 60^{circ}=sqrt{3}r}).
Радиус второй окружности, вписанной в первый треугольник: (mathrm{r_2=frac{a_1}{2}tg30^{circ}=frac{a_1}{2sqrt{3}}=frac{sqrt{3}r}{2sqrt{3}}=frac{r}{2}})
Сторона правильного треугольника, вписанного во вторую окружность: (mathrm{a_2=sqrt{3}r_2=frac{sqrt{3}r}{2}}).
Радиус третьей окружности, вписанной во второй треугольник: (mathrm{r_3=frac{r_2}{2}=frac{r}{4}}).
Получаем геометрическую прогрессию для сторон треугольников: $$ mathrm{ a_1=sqrt{3}r, a_2=frac{sqrt{3}r}{2}, a_3=frac{sqrt{3}r}{4}=,…, q=frac12 } $$ и геометрическую прогрессию для радиусов окружностей: $$ mathrm{ r_1=r, r_2=frac{r}{2}, r_3=frac{r}{4},…, q=frac12 } $$ Геометрическая прогрессия для периметров треугольников: $$ mathrm{ p_1=3a_1=3sqrt{3}r, p_2=frac{3sqrt{3}r}{2}, p_3=frac{3sqrt{3}r}{4},…, q=frac12 } $$ Сумма всех периметров: begin{gather*} mathrm{ S_p=frac{p_1}{1-q}=2p_1=6sqrt{3}r} end{gather*} Геометрическая прогрессия для длин всех окружностей: $$ mathrm{ L_1=2pi r_2=2pi r, L_2=pi r, L_3=frac{pi r}{2},…, frac12 } $$ Сумма всех длин окружностей: $$ mathrm{ S_L=frac{L_1}{1-q}=2L_1=4pi r } $$ Ответ: (mathrm{S_p=6sqrt{3}r, S_L=4pi r})