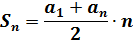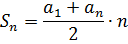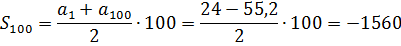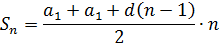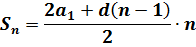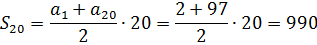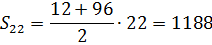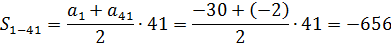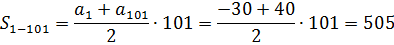Сумма n первых членов арифметической прогрессии — штука довольно простая и понятная. Как по смыслу, так и по формуле. Но задания на эту тему встречаются самые разные. От примитивных до вполне себе серьёзных. Имеет смысл разобраться, правда?)
Очень часто во всевозможных задачках на арифметическую прогрессию требуется найти сумму некоторого количества её членов. Если этих самых членов мало, то складывать, конечно, и безо всяких формул можно. А вот если много, то сложение «вручную» уже напрягает, да… В этих случаях и выручает формула.)
Итак, вот она, формула суммы n первых членов арифметической прогрессии:
Для начала, как водится, разберёмся с названием и со смыслом формулы суммы. А потом и задачки порешаем. В своё удовольствие.)
Ключевыми словами в названии формулы являются слова «n первых членов». Эти слова всего лишь означают, что берётся последовательность
(an): a1, a2, a3, a4, a5, …, an
и аккуратно суммируются (т.е. складываются) все её члены. С первого члена (a1) по последний (an). Причём складываются именно все члены подряд, без пропусков! Это важно.
Смысл формулы суммы прост до неприличия. Эта формула позволяет легко и быстро находить сумму любого количества членов любой арифметической прогрессии с первого по n-й. Не складывая все числа по порядочку.)
А теперь, традиционно, разбираемся со всеми буковками и символами, сидящими в формуле. Это очень многое прояснит.
Sn — та самая сумма n первых членов, которую мы ищем. Результат сложения всех членов арифметической прогрессии с первого по последний. Ещё раз напоминаю, что сумма считается именно (и только) с первого члена. Дело всё в том, что частенько встречаются задачки типа: «найти сумму пятого и восьмого членов». Или: «найти сумму всех членов с десятого по тридцатый». В таких задачках прямое применение формулы суммы не катит, да…)
a1 — первый член прогрессии. Здесь, думаю, комментарии излишни.)
an — последний член прогрессии. Под номером n. Да, не очень привычное название, но для работы с суммой — очень удобное.) Что это такое — об этом ниже.
n — номер последнего члена.
Вот и всё. Все обозначения расшифрованы. Осталось лишь разобраться, что же такое последний член.
Для начала задам такой хитрый вопрос: как вы думаете, какой член будет последним, если нам дана бесконечная арифметическая прогрессия? Ответ очевиден: никакой.) Какой бы член an и с каким бы номером n мы ни взяли, для него всегда найдётся следующий, (n+1)-й член.
Поэтому говорить о конкретной конечной сумме для бесконечной арифметической прогрессии (с бесконечным числом членов) попросту нету никакого смысла. Не существует такой суммы. Бесконечная она… Кстати, в отличие от геометрической прогрессии, сумму бесконечного числа членов которой, в некоторых случаях, найти… можно.) Но о геометрической прогрессии и о такой интересной бесконечной сумме — в соответствующих уроках.)
Короче говоря, когда мы имеем дело с суммой арифметической прогрессии, то нам всегда требуется некоторый конечный член. Тот член, на котором следует остановиться. Которым следует ограничиться. Чтобы не складывать все члены до бесконечности.) Вот именно этот граничный член an — и есть последний член прогрессии. И все дела.)
Номер этого самого последнего члена (т.е. n) определяется исключительно заданием. Либо он указан в условии прямым текстом, либо же косвенно, в зашифрованном виде.) А составители заданий, порой, шифруют эту ценную информацию (последний член и номер последнего члена) с безграничной фантазией, да…) Для грамотной расшифровки надо, во-первых, понимать смысл арифметической прогрессии, во-вторых, не бояться и думать головой и… внимательно читать задание.) Иначе — никак. Чуть ниже, в конкретных задачках мы все эти секреты пораскрываем.
Как выводится формула суммы?
Вывод формулы суммы n первых членов арифметической прогрессии хоть и прост, но весьма оригинален по сравнению с выводом формулы n-го члена.) Для этого придётся нам запустить машину времени и плавно переместиться… нет, не в будущее.) Мы переместимся в Германию конца XVIII века. Жил-был в то время великий немецкий математик Карл Фридрих Гаусс. Король математики! Одарённость его просто не знала границ!
Так вот, согласно легенде, когда Гаусс был ещё школьником, учитель дал детям задание. Скучно им, видите ли, было на уроке… А именно — посчитать сумму всех натуральных чисел от 1 до 100. Для всего класса это задание и впрямь оказалось работёнкой не из лёгких. На целый урок.) Но… только не для юного вундеркинда Гаусса с его нестандартным мышлением.) Как он выкрутился? Он заметил, что попарные суммы чисел с противоположных концов всегда одинаковы: 1+100=101, 2+99=101, 3+98=101 и так далее.) Всего таких попарных сумм, очевидно, будет 50. Рассуждая таким образом, Гаусс, к удивлению учителя, дал верный ответ за полминуты:
1+2+3+…+100 = 50·101 = 5050
И всё! Здорово, правда?)
Для вывода нашей формулы, мы поступим так же мудро, как и Гаусс. По такому же принципу. Смотрите, сейчас интересно будет! Запишем сначала нашу прогрессию (an) в виде прямой последовательности:
a1, a2, a3, …, an-2, an-1, an.
А теперь запишем эту же прогрессию, но в виде обратной последовательности. Член an будет на первом месте, а a1 — на последнем.
Вот так:
an, an-1, an-2, …, a3, a2, a1.
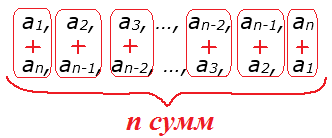
А теперь (внимание!) берём и попарно складываем между собой члены обеих последовательностей — прямой и обратной.
Вот так:
Получаем ровно «n» попарных сумм. Как вы думаете, что в итоге мы получим, если сложим между собой все эти n сумм? Очевидно, нужную нам сумму n первых членов арифметической прогрессии Sn, но… удвоенную. Что правда то правда: сначала мы складываем все члены с 1-го по n-й, а затем — наоборот. И, если сложить оба результата, то получим, как раз, удвоенную сумму членов с 1-го по n-й. То есть, 2Sn.
Можно смело записать:
2Sn = (а1+an)+(a2+an-1)+(a3+an-2)+…+(an-2+a3)+(an-1+a2)+(an+a1)
А теперь разберёмся со всеми «лишними» скобочками и буковками. Сейчас будет ещё интереснее!
Как вы уже, возможно, заметили, скобки, стоящие в сумме на одинаковых местах с начала и с конца, совершенно одинаковые! Только слагаемые переставлены местами.) Первые и последние скобки мы трогать не будем. Посмотрим, что получается во вторых и предпоследних скобках. Для этого представим a2 как a1+d, а an-1 представим как an—d. Прямо по смыслу арифметической прогрессии:
a2 = a1 + d
an-1 = an — d
Подставим это добро во вторую (и предпоследнюю) скобки. Что получим:
(a2+an-1) = (an-1+a2) = a1 + d + an — d = a1 + an
Рассуждая аналогичным образом, для третьих скобок с начала и с конца мы получим:
(a3+an-2) = (an-2+a3) = a1 + 2d + an — 2d = a1 + an
Ну как? Улавливаете идею? Да! Каждая из попарных сумм членов, стоящих на одинаковых местах с начала и с конца в нашей общей сумме 2Sn, всегда будет одна и та же. И равна a1 + an. То есть, сумме первого и последнего членов. А всего таких попарных сумм у нас сколько? Правильно, «n» штук! Столько же, сколько и членов в прогрессии, да…) Не зря же я картинки рисую иногда.
Вот и пишем:
2Sn = (а1+an)·n
Выражая из этого равенства Sn, получаем требуемую формулу:
Вот и всё.)
Ну что, со смыслом формулы разобрались. С выводом — тоже. Я вижу, вам уже не терпится начать решать задачки. Что ж, поехали!
Решение задач на сумму арифметической прогрессии.
Начнём с несложной задачки. Безо всяких фокусов.)
1. Дана арифметическая прогрессия:
24; 23,2; 22,4; 21,6; …
Найти сумму первых ста её членов.
Прогрессия нам задана в виде последовательности. Можно, конечно, уловить закономерность, продлить эту последовательность, выписать первые сто её членов, сложить их да посчитать, но… как-то тупо и долго получается, не находите? Но мы же с вами народ учёный. Формулу суммы знаем.) Вот и запустим её в дело.
Сразу пишем формулу суммы:
А теперь смотрим на формулу и соображаем, какие элементы формулы нам даны, а чего не хватает.
Первый член a1 известен? Да! Это 24. А последний член an? Пока нет… Но… зато нам известен его номер n! Это 100 (n = 100). В задании прямым текстом сказано: найти сумму первых ста членов. Стало быть, последним членом прогрессии будет сотый член a100. И как его отыскать? Считать и выписывать сто членов? Зачем!?) Ведь мы же не слепые, глазками последовательность видим, а смысл арифметической прогрессии — понимаем.
Стало быть, можем посчитать разность прогрессии и затем найти интересующий нас сотый член по формуле n-го члена:
an = a1 + (n-1)·d
Вот и трудимся. Для разности d берём любой член последовательности (кроме первого) и отнимаем предыдущий.
ЕЩЁ РАЗ ВНИМАНИЕ!!! Не просто считаем разницу между большим и меньшим соседними членами (типа 23,2-22,4), а именно от выбранного члена (23,2) отнимаем предыдущий (24)!
Почему ругаюсь? Потому что это весьма и весьма распространённые грабли, на которые наступает значительная часть учеников, теряя драгоценные баллы на контрольных и экзаменах и получая заслуженные минусы. Особенно часто этот косяк встречается в убывающих прогрессиях и в прогрессиях с отрицательными членами.
Вот и считаем правильно. Например, так:
d = 23,2 — 24 = -0,8
Вот так. Разность — отрицательна. Прогрессия — убывает. Как и в задании.)
Считаем сотый член по формуле n-го члена:
a100 = a1 + (-0,8)·(100-1) = 24-0,8·99 = -55,2
Есть. Мы выяснили все интересующие нас параметры в формуле суммы. Осталось подставить их да посчитать:
Ответ: -1560
Кстати сказать, если подставить в формулу суммы вместо an его выражение через формулу n-го члена, то получим:
Или, если привести подобные в числителе:
Эта формула — тоже формула суммы n первых членов арифметической прогрессии. Только записанная в другом виде — через первый член и разность прогрессии. В некоторых задачках эта модифицированная формула здорово выручает, да.) Имеет смысл запомнить. Или, в случае чего, уметь вывести, как здесь. Ведь формулу n-го члена в любом случае надо помнить.)
Следующая задачка. На основе реального варианта ОГЭ:
2. Арифметическая прогрессия задана условием: an = -3 + 5n. Найдите сумму первых двадцати её членов.
Хорошая задачка. Лёгкая.) Настолько лёгкая, что народ тут же косячит… НЕ НАДО писать сразу, что первый член — минус три! Это фатальное заблуждение, да… Ибо прогрессия нам задана видоизменённой формулой n-го члена. Как работать с такой формулой, подробно рассказано по ссылке. Кто не в курсе — кликаем и читаем.) Кто в курсе, делаем всё как положено. А именно — подставляем в формулу вместо n единичку и считаем:
a1 = -3+5·1 = 2
Вот так вот. Первый член — двойка, а не минус три…
Что там нам ещё нужно для суммы? Последний член и номер последнего члена? Пожалуйста! Нас спрашивают про сумму двадцати первых членов. Стало быть, в качестве последнего члена у нас будет выступать a20, а номером n последнего члена будет, знамо дело, двадцатка.
Вот и считаем a20 подставляя n = 20 в формулу n-го члена:
a20 = -3+5·20 = 97
А теперь уже считаем нужную нам сумму:
Ответ: 990
А теперь задачка более творческая. 
3. Найти сумму всех натуральных двузначных чисел, кратных четырём.
Во! Ни первого члена нет, ни последнего, ни номера n, ни прогрессии вообще… Что делать?!
Что-что… Головой думать, да.) И вытаскивать из условия задачи все элементы формулы суммы арифметической прогрессии. Ибо здесь, как раз, тот самый случай, когда ключевые параметры прогрессии в условии ловко зашифрованы.
Вот и начинаем расшифровку. Что такое натуральные числа — знаем. То есть, целые положительные. Что такое двузначные числа — тоже знаем. Ну, те, что из двух циферок состоят.) Какое же двузначное число будет первым? 10, ясное дело.) А последнее двузначное число? Очевидно, 99. За ним уже трёхзначные числа пойдут…
Идём дальше. Кратные четырём… Это что значит? Это значит, делящиеся на четыре нацело! Десятка делится на четыре? Не делится! 11 — тоже не делится. 12… делится! Если ещё немного подумать, то можно сообразить, что последнее такое число будет 96. Отлично! Очень многое проясняется! Теперь уже можно записать последовательность по условию задачки:
12, 16, 20, …, 92, 96.
Будет эта последовательность арифметической прогрессией? А как же! Каждый член отличается от предыдущего строго на четвёрку. Если к члену прибавить, скажем, 3 или 5, то новое число уже не поделится нацело на 4.
Сразу же можем и разность прогрессии посчитать:
d = 4
Пригодится.)
Ну вот. Теперь мы уже с вами знаем кое-какие параметры прогрессии:
a1 = 12
d = 4
an = 96
А каков будет номер n последнего члена 96? А вот тут два пути решения. Первый путь — для сверхтрудолюбивых, но некультурных. Можно расписать всю прогрессию да посчитать пальчиком количество членов. А второй путь — для ленивых, зато культурных.) Я отношусь к ленивым, поэтому выберу второе. А именно — распишу последний член прогрессии (т.е. 96) по формуле n-го члена, подставляя уже известные нам данные:
96 = a1 + d(n-1)
96 = 12 + 4(n-1)
4(n-1) = 84
n-1 = 21
n = 22
Вот так. Значит, число 96 — это двадцать второй член нашей прогрессии.
А теперь смотрим на формулу суммы:
Смотрим и… прыгаем от радости!) Ибо мы вытащили из условия задачи все необходимые данные для подсчёта требуемой суммы. Незаметно для себя. Вот они:
a1 = 12
a22 = 96
n = 22
Sn = S22
Осталось лишь подставить да посчитать:
Ответ: 1188
Рассмотрим теперь ещё один тип популярных задачек. На первый взгляд, всё очень похоже, да не совсем…)
4. Дана арифметическая прогрессия:
-30; -29,3; -28,6; …
Найдите сумму членов с 42-го по 101-й.
И как вам? Прямое применение формулы суммы разочарует. Напоминаю, что формула считает сумму только с первого члена. А в нашей задаче надо считать сумму с сорок второго… Тупик? Ну да, щас!)
Можно, конечно, расписать всю прогрессию до 101-го члена и посчитать столбиком на бумажке все члены с 42-го по 101-й. Но возьмутся за это увлекательное занятие только откровенные мазохисты, да…)
Мы же поступим просто и элегантно.) А именно — разобьём нашу прогрессию на две части. Первая часть будет с первого члена по 41-й. А вторая часть — с 42-го члена по 101-й. Ясно, что если мы посчитаем сумму членов первой части S1-41 и сложим её с суммой членов второй части S42-101, то получим сумму членов прогрессии с первого по сто первый S1-101.
В математической записи:
S1-41 + S42-101 = S1-101
Из этого равенства видно, что найти нужную нам сумму S42-101 можно простым вычитанием:
S42-101 = S1-101 — S1-41
Вот теперь всё встало на свои места! Обе суммы справа считаются с первого члена. Стало быть, к ним уже применима наша стандартная формула суммы. Ну что, начнём?
Первым делом вытаскиваем из условия задачи ключевые параметры прогрессии:
a1 = -30
d = 0,7
Кроме того, для расчёта сумм S1-41 и S1-101 нам понадобятся 41-й и 101-й члены. Считаем их по формуле n-го члена:
a41 = a1+40d = -30+40·0,7 = -30+28 = -2
a101 = a1+100d = -30+100·0,7 = -30+70 = 40
Теперь считаем суммы S1-41 и S1-101 по формуле:
Остались сущие пустяки. От суммы 101 члена отнять сумму 41 члена:
S42-101 = S1-101 — S1-41 = 505 — (-656) = 1161
Ответ: 1161
Вот и всё.) Обратите внимание на одну очень полезную фишку. Вместо прямого расчёта того что нам нужно (S42-101), мы вычислили то, что, казалось бы, совершенно не нужно (S1-41). А уже потом посчитали и S42-101, отбросив от полного результата ненужное. В злых задачках такой искусный манёвр очень часто спасает.)
В этом небольшом уроке мы рассмотрели задачки, для успешного решения которых достаточно понимать смысл суммы n первых членов арифметической. Ну и парочку формул знать надо, да.)
Подытожим наш урок практическим советом:
При решении любой задачи на сумму членов арифметической прогрессии настоятельно рекомендую выписать две ключевые формулы.
Формулу n-го члена:
an = a1 + (n-1)·d
Формулу суммы n первых членов арифметической прогрессии:
Эти две формулы обязательно подскажут, что именно надо делать, в каком направлении двигаться, чтобы справиться с задачей. Проверено! Помогает.
А теперь решаем самостоятельно.
1. Найти сумму всех натуральных двузначных чисел, которые не делятся нацело на четыре.
Что, круто, да?) Подсказка спрятана в комментарии к последней разобранной задаче №4. Ну и результат предпоследней задачки №3 поможет.)
2. Арифметическая прогрессия задана условиями:
a1 = -3,1
an+1 = an+0,9
Найдите сумму первых 19 её членов.
Да-да, это рекуррентная формула, которую многие так не любят. Задачки с такой формулой мы в этом уроке не рассматривали. А чего их рассматривать? Их решать надо.) Материала этого урока вполне достаточно, чтобы справиться с заданием. Про рекуррентную формулу и как именно с ней работать можно прочитать в предыдущем уроке. Не пренебрегайте этой задачкой, такие частенько встречаются в ОГЭ!
3. Марфуша была сладкоежкой и очень любила пирожные с кремом и шоколадной глазурью. Каждое пирожное стоит 60 рублей. Накопив 2700 рублей, Марфуша решила устроить себе сладкую жизнь: в первый день купить и съесть всего одно пирожное, а в каждый последующий день покупать и съедать на одно пирожное больше. Пока не истратит всю накопленную заначку.
а) сколько пирожных в итоге купила и съела Марфуша?
б) сколько дней сладкой жизни получилось у Марфуши?
Сложно? Поможет дополнительная формула суммы из разобранной задачи №1. Ну и решение квадратных уравнений тоже надо вспомнить, да.)
Ответы (в беспорядке): 9; 95; 45; 3717.
Арифметическая прогрессия — коротко о главном
Определение арифметической прогрессии:
Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна ( displaystyle d).
Например:
- ( {{a}_{1}}=3)
- ( displaystyle {{a}_{2}}=3+d=7~Rightarrow d=7-3=4)
- ( displaystyle {{a}_{3}}=7+4=11) и т.д.
Арифметическая прогрессия бывает возрастающей (( displaystyle d>0)) и убывающей (( displaystyle d<0)).
Формула нахождения n-ого члена арифметической прогрессии:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) , где ( displaystyle n)– количество чисел в прогрессии.
Как найти член прогрессии, если известны его соседние члены:
( {{text{a}}_{text{n}}}=frac{{{text{a}}_{text{n}+1}}+{{text{a}}_{text{n}-1}}}{2}) — где ( displaystyle n) – количество чисел в прогрессии.
Сумма членов арифметической прогрессии:
1-й способ: ( {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.
2-й способ: ( displaystyle {{s}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.
Числовая последовательность
Итак, сядем и начнем писать какие-нибудь числа. Например: ( displaystyle 4,text{ }7,text{ }-8,text{ }13,text{ }-5,text{ }-6,text{ }0,text{ }ldots )
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ( displaystyle 7)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.
Это и есть пример числовой последовательности.
Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:
Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и ( displaystyle n)-ное число) всегда одно.
Число с номером ( displaystyle n) называется ( displaystyle n)-ным членом последовательности.
Всю последовательность мы обычно называем какой-нибудь буквой (например, ( displaystyle a)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: ( displaystyle {{a}_{1}},text{ }{{a}_{2}},text{ }…,text{ }{{a}_{10}},text{ }…,text{ }{{a}_{n}}).
Арифметическая прогрессия — определения
Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.
Например:
( begin{array}{l}{{a}_{1}}=3\{{a}_{2}}=3+d=7~~~Rightarrow ~d=7-3=4\{{a}_{3}}=7+4=11end{array})
Такая числовая последовательность называется арифметической прогрессией.
Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.
Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.
Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:
- ( displaystyle 3;text{ }6;text{ }9;text{ }12;text{ }15;text{ }17ldots )
- ( displaystyle 1;text{ }12;text{ }23;text{ }34;text{ }45text{ }ldots )
- ( displaystyle -5;text{ }-1;text{ }3;text{ }7;text{ }11;text{ }15ldots )
- ( displaystyle -6;text{ }5;text{ }17;text{ }28;text{ }39ldots )
Разобрался? Сравним наши ответы:
Является арифметической прогрессией – 2, 3.
Не является арифметической прогрессией – 1, 4.
Вернемся к заданной прогрессии (( displaystyle 3;text{ }7;text{ }11;text{ }15;text{ }19ldots )) и попробуем найти значение ее 6-го члена.
Существует два способа его нахождения.
Нахождения n-ого члена арифметической прогрессии
Способ I
Мы можем прибавлять к предыдущему значению числа прогрессии ( d=4) , пока не дойдем до ( displaystyle 6)-го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:
( begin{array}{l}{{a}_{4}}=11+4=15\{{a}_{5}}=15+4=19\{{a}_{6}}=19+4=23end{array})
Итак, 6-ой член описанной арифметической прогрессии равен 23.
Способ II
А что если нам нужно было бы найти значение ( displaystyle 140)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.
А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.
Это и есть математика!
Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка.
Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.
Что мы знаем?
- У нас есть арифметическая прогрессия: 3, 7, 11, 15, 19 и т.д.
- У нас есть номера прогрессии: 1, 2, 3, 4, 5, и т.д.
- Мы все время прибавляем 4, значит разница прогрессии d = 4.
Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.
7=3+4 или 7=3+d
Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?
11=3+4+4 или 11=3+d+d
Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.
Давай проверим? Чему равен 4-й член арифметической прогрессии?
15=3+4+4+4 или 15=3+d+d+d
Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!
Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа.
А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.
Например, посмотрим, из чего складывается значение ( displaystyle 4)-го члена данной арифметической прогрессии:
( begin{array}{l}{{a}_{4}}={{a}_{1}}+dleft( 4-1 right)\{{a}_{4}}=3+4left( 4-1 right)=15end{array})
Попробуй самостоятельно найти таким способом значение члена ( displaystyle n=6) данной арифметической прогрессии.
Рассчитал? Сравни свои записи с ответом:
( begin{array}{l}{{a}_{6}}={{a}_{1}}+dleft( 6-1 right)\{{a}_{6}}=3+4left( 6-1 right)=3+4cdot 5=3+20=23end{array})
Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли ( displaystyle d) к предыдущему значению членов арифметической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) – уравнение арифметической прогрессии.
Кстати, таким образом мы можем посчитать и ( displaystyle 140)-ой член данной арифметической прогрессии (да и ( displaystyle 169)-ый тоже можем, да и любой другой вычислить совсем несложно).
Попробуй посчитать значения ( displaystyle 140)-го и ( displaystyle 169)-го членов, применив полученную формулу.
( begin{array}{l}…\{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=3+4left( 140-1 right)=3+4cdot 139=3+556=559\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=3+4left( 169-1 right)=3+4cdot 168=3+672=675end{array})
Возрастающие и убывающие арифметические прогрессии
Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.
Например:
( displaystyle begin{array}{l}4;text{ }6;text{ }8;text{ }10;text{ }12\-2;text{ }4;text{ }10;text{ }16;text{ }20end{array})
Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.
Например:
( displaystyle begin{array}{l}12;text{ }10;text{ }8;text{ }6;text{ }4\4;text{ }0;text{ }-4;text{ }-8;text{ }-12.end{array})
Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.
Проверим это на практике.
Нам дана арифметическая прогрессия, состоящая из следующих чисел: ( displaystyle 13;text{ }8;text{ }4;text{ }0;text{ }-4.)
Проверим, какое получится ( displaystyle 4)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:
( {{text{a}}_{text{n}}}={{text{a}}_{1}}+text{d}left( text{n}-1 right))
Заметим, что так как арифметическая прогрессия убывающая, то значение ( displaystyle d) будет отрицательным, ведь каждый последующий член меньше предыдущего.
( displaystyle d=8-13=-5)
( {{a}_{4}}={{a}_{1}}+dleft( 4-1 right))
Так как ( displaystyle d=-5), то:
( {{a}_{4}}=13-5left( 4-1 right)=13-15=-2)
Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.
Попробуй самостоятельно найти ( displaystyle 140)-ой и ( displaystyle 169)-ый члены этой арифметической прогрессии.
Сравним полученные результаты:
( begin{array}{l}{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=13-5left( 140-1 right)=13-5cdot 139=13-695=-682\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=13-5left( 169-1 right)=13-5cdot 168=13-840=-827end{array})
Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)
Усложним задачу — выведем свойство арифметической прогрессии.
Допустим, нам дано такое условие:
( displaystyle 4;text{ }x;text{ }12ldots ) — арифметическая прогрессия, найти значение ( displaystyle x).
Легко, скажешь ты и начнешь считать по уже известной тебе формуле:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))
Пусть ( displaystyle {{a}_{1}}=4), а ( displaystyle {{a}_{3}}=12), тогда:
( displaystyle begin{array}{l}{{a}_{3}}={{a}_{1}}+dleft( 3-1 right)\12=4+2d~~Rightarrow ~d=frac{12-4}{2}=4\{{a}_{2}}=x={{a}_{1}}+d\{{a}_{2}}=x=4+4=8end{array})
Абсолютно верно.
Получается, мы сначала находим ( displaystyle d), потом прибавляем его к первому числу и получаем искомое ( displaystyle x).
Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа ( displaystyle 4024;~x;6072)?
Согласись, есть вероятность ошибиться в вычислениях.
А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?
Конечно да, и именно ее мы попробуем сейчас вывести.
Обозначим искомый член арифметической прогрессии как ( {{text{a}}_{text{n}}}), формула его нахождения нам известна – это та самая формула, выведенная нами в начале:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)), тогда:
- предыдущий член прогрессии это ( {{a}_{n}}-d): ( {{a}_{n-1}}={{a}_{1}}+dleft( n-1 right)-d)
- последующий член прогрессии это ( {{a}_{n}}+d): ( {{a}_{n+1}}={{a}_{1}}+dleft( n-1 right)+d)
Просуммируем предыдущий и последующий члены прогрессии:
( {{a}_{1}}+dleft( n-1 right)-d+{{{a}}_{1}}+text{d}left( text{n}-1 right)+text{d}=2left( {{a}_{1}}+dleft( n-1 right) right)text{ }!!~!!text{ })
Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.
Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на ( 2).
( {{a}_{n}}=frac{{{a}_{n+1}}+{{a}_{n-1}}}{2}) – свойство членов арифметической прогрессии.
Попробуем посчитать значение ( x), используя выведенную формулу:
( x=frac{4+12}{2}=8)
Все верно, мы получили это же число. Закрепим материал.
Посчитай значение ( x) для прогрессии ( displaystyle 4024;~x;6072) самостоятельно, ведь это совсем несложно.
( x=frac{4024+6072}{2}=5048)
Молодец! Ты знаешь о прогрессии почти все!
Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…
Сумма первых n членов арифметической прогрессии
Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:
«Сосчитать сумму всех натуральных чисел от ( displaystyle 1) до ( displaystyle 40) (по другим источникам до ( displaystyle 100)) включительно».
Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…
Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.
Допустим, у нас есть арифметическая прогрессия, состоящая из ( displaystyle 6)-ти членов: ( displaystyle 6;text{ }8;text{ }10;text{ }12;text{ }14;text{ }16…)
Нам необходимо найти сумму данных ( displaystyle 6) членов арифметической прогрессии.
Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму ( displaystyle 100) ее членов, как это искал Гаусс?
Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.
Попробовал? Что ты заметил? Правильно! Их суммы равны
А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?
Конечно, ровно половина всех чисел, то есть ( frac{6}{2}=3).
Исходя из того, что сумма двух членов арифметической прогрессии равна ( 22), а подобных равных пар ( 3), мы получаем, что общая сумма равна:
( displaystyle Stext{ }=text{ }22cdot 3text{ }=text{ }66).
Таким образом, формула для суммы первых ( displaystyle n) членов любой арифметической прогрессии будет такой:
( displaystyle {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.
В некоторых задачах нам неизвестен ( displaystyle n)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу ( displaystyle n)-го члена. ( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))
Что у тебя получилось?
( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.
Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма ( displaystyle 40) чисел, начиная от ( displaystyle 1)-го, и сумма ( displaystyle 100) чисел начиная от ( displaystyle 1)-го.
Сколько у тебя получилось?
У Гаусса получилось, что сумма ( displaystyle 100 ) членов равна ( displaystyle 5050), а сумма ( displaystyle 40 ) членов ( displaystyle 820).
Так ли ты решал?
- ( {{S}_{40}}=frac{left( 1+40 right)cdot 40}{2}=frac{41cdot 40}{2}=frac{1640}{2}=820)
- ( {{S}_{100}}=frac{left( 1+100 right)cdot 100}{2}=frac{101cdot 100}{2}=5050)
На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.
Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.
Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется ( displaystyle 6) блочных кирпичей.
Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?
В данном случае прогрессия выглядит следующим образом:
( displaystyle 6;text{ }5;text{ }4;text{ }3;text{ }2; 1).
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Способ 1.
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\~~{{S}_{6}}=frac{left( 6+1 right)cdot 6}{2}=frac{7cdot 6}{2}=21\~end{array})
Способ 2.
( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n)
( {{S}_{n}}=frac{2cdot 6+1left( 6-1 right)}{2}cdot 6=frac{12+5cdot 6}{2}=frac{7cdot 6}{2}=frac{42}{2}=21)
А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.
Сошлось?
Молодец, ты освоил сумму ( displaystyle n)-ных членов арифметической прогрессии.
Конечно, из ( displaystyle 6) блоков в основании пирамиду не построишь, а вот из ( displaystyle 60)?
Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – ( displaystyle 1830) блоков:
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\{{S}_{60}}=frac{left( 60+1 right)cdot 60}{2}=frac{61cdot 60}{2}=61cdot 30=1830.end{array})
Когда речь идет о таком параметре, как сумма арифметической прогрессии, подразумевается всегда сумма первых членов арифметической прогрессии или сумма членов прогрессии с k по n, то есть количество членов, которые берутся для суммы, строго ограничено в заданных условием пределах. В противном случае задание не будет иметь решения, так как вся числовая последовательность именно арифметической прогрессии начинается с конкретного числа — первого члена a1, и продолжается бесконечно.
Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.
a1+an=a2+a(n-1)=a3+a(n-2)=⋯
Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии
Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.
В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Числовые последовательности (основные понятия)
Арифметическая прогрессия
Геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия
Связь арифметической и геометрической прогрессий
Числовые последовательности (основные понятия)
Если каждому натуральному числу n поставить в соответствие действительное число an, то говорят, что задано числовую последовательность:
a1, a2, a3, . . . , an, . . . .
Итак, числовая последовательность — функция натурального аргумента.
Число a1 называют первым членом последовательности, число a2 — вторым членом последовательности, число a3 — третьим и так далее. Число an называют n-м членом последовательности, а натуральное число n — его номером.
Из двух соседних членов an и an+1 последовательности член an+1 называют последующим (по отношению к an), а an — предыдущим (по отношению к an+1).
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью формулы n-го члена, то есть формулы, которая позволяет определить член последовательности по его номеру.
► Например,
последовательность положительных нечётных чисел можно задать формулой
an = 2n –1,
а последовательность чередующихся 1 и –1 — формулой
bn = (–1)n+1. ◄
Последовательность можно определить рекуррентной формулой, то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.
► Например,
если a1 = 1, а an+1 = an + 5, то первые пять членов последовательности находим следующим образом:
a1 = 1,
a2 = a1 + 5 = 1 + 5 = 6,
a3 = a2 + 5 = 6 + 5 = 11,
a4 = a3 + 5 = 11 + 5 = 16,
a5 = a4 + 5 = 16 + 5 = 21.
Если а1 = 1, а2 = 1, an+2 = an + an+1, то первые семь членов числовой последовательности устанавливаем следующим образом:
a1 = 1,
a2 = 1,
a3 = a1 + a2 = 1 + 1 = 2,
a4 = a2 + a3 = 1 + 2 = 3,
a5 = a3 + a4 = 2 + 3 = 5,
a6 = a4 + a5 = 3 + 5 = 8,
a7 = a5 + a6 = 5 + 8 = 13. ◄
Последовательности могут быть конечными и бесконечными.
Последовательность называется конечной, если она имеет конечное число членов. Последовательность называется бесконечной, если она имеет бесконечно много членов.
► Например,
последовательность двузначных натуральных чисел:
10, 11, 12, 13, . . . , 98, 99
конечная.
Последовательность простых чисел:
2, 3, 5, 7, 11, 13, . . .
бесконечная. ◄
Последовательность называют возрастающей, если каждый её член, начиная со второго, больше чем предыдущий.
Последовательность называют убывающей, если каждый её член, начиная со второго, меньше чем предыдущий.
► Например,
2, 4, 6, 8, . . . , 2n, . . . — возрастающая последовательность;
1, 1/2, 1/3, 1/4, . . . , 1/n, . . . — убывающая последовательность. ◄
Последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают, называется монотонной последовательностью.
Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.
Арифметическая прогрессия
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
Иначе,
a1, a2, a3, . . . , an, . . .
является арифметической прогрессией, если для любого натурального числа n выполняется условие:
an+1 = an + d,
где d — некоторое число.
Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:
а2 – a1 = а3 – a2 = . . . = an+1 – an = d.
Число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.
► Например,
если a1 = 3, d = 4, то первые пять членов последовательности находим следующим образом:
a1 =3,
a2 = a1 + d = 3 + 4 = 7,
a3 = a2 + d = 7 + 4 = 11,
a4 = a3 + d = 11 + 4 = 15,
a5 = a4 + d = 15 + 4 = 19. ◄
Для арифметической прогрессии с первым членом a1 и разностью d её n-й член может быть найден по формуле:
an = a1 + (n – 1)d.
► Например,
найдём тридцатый член арифметической прогрессии
1, 4, 7, 10, . . .
Имеем,
a1 =1, d = 3,
a30 = a1 + (30 – 1)d =1 + 29·3 = 88. ◄
Так как
an–1 = a1 + (n – 2)d,
an = a1 + (n – 1)d,
an+1 = a1 + nd,
то, очевидно,
то есть,
каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.
► Например,
докажем, что последовательность, которая задаётся формулой an = 2n – 7, является арифметической прогрессией.
Воспользуемся приведённым выше утверждением. Имеем:
an = 2n – 7,
an–1 = 2(n – 1) – 7 = 2n – 9,
an+1 = 2(n + 1) – 7 = 2n – 5.
Следовательно,
| an+1 + an–1 |
= |
2n – 5 + 2n – 9 |
= 2n – 7 = an, |
| 2 |
2 |
что и доказывает нужное утверждение. ◄
Отметим, что n-й член арифметической прогрессии можно найти не толь через a1, но и любой предыдущий ak, для чего достаточно воспользоваться формулой
an = ak + (n – k)d.
► Например,
для a5 можно записать
a5 = a1 + 4d,
a5 = a2 + 3d,
a5 = a3 + 2d,
a5 = a4 + d. ◄
Так как
an = an–k + kd,
an = an+k – kd,
то, очевидно,
то есть,
любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.
Кроме того, для любой арифметической прогрессии справедливо равенство:
am + an = ak + al,
если
m + n = k + l.
► Например,
в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
1) a10 = 28 = (25 + 31)/2 = (a9 + a11)/2;
2) 28 = a10 = a3 + 7d = 7 + 7·3 = 7 + 21 = 28;
3) a10 = 28 = (19 + 37)/2 = (a7 + a13)/2;
4) a2 + a12 = a5 + a9, так как
a2 + a12 = 4 + 34 = 38,
a5 + a9 = 13 + 25 = 38. ◄
Сумма
Sn = a1 + a2+ a3 + . . .+an,
первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Отсюда, в частности, следует, что если нужно просуммировать члены
ak, ak+1, . . . , an,
то предыдущая формула сохраняет свою структуру:
| Sn – Sk–1 = ak + ak+1 + . . . + an = | ak + an |
· (n – k + 1) . |
| 2 |
► Например,
в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
S10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;
10 + 13 + 16 + 19 + 22 + 25 + 28 = S10 – S3 = (10 + 28) · (10 – 4 + 1)/2 = 133. ◄
Если дана арифметическая прогрессия, то величины a1, an, d, n и Sn связаны двумя формулами:
| an = a1 + (n – 1)d и Sn = | a1 + an |
· n . |
| 2 |
Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Арифметическая прогрессия является монотонной последовательностью. При этом:
- если d > 0, то она является возрастающей;
- если d < 0, то она является убывающей;
- если d = 0, то последовательность будет стационарной.
Геометрическая прогрессия
Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Иначе,
b1, b2, b3, . . . , bn, . . .
является геометрической прогрессией, если для любого натурального числа n выполняется условие:
bn+1 = bn · q,
где q ≠ 0 — некоторое число.
Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:
b2/b1 = b3/b2 = . . . = bn+1/bn = q.
Число q называют знаменателем геометрической прогрессии.
Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.
► Например,
если b1 = 1, q = –3, то первые пять членов последовательности находим следующим образом:
b1 = 1,
b2 = b1 ·
q = 1 · (–3) = –3,
b3 = b2 ·
q = –3 · (–3) = 9,
b4 = b3 ·
q = 9 · (–3) = –27,
b5 = b4 ·
q = –27 · (–3) = 81. ◄
Для геометрической прогрессии с первым членом b1 и знаменателем q её n-й член может быть найден по формуле:
bn = b1 ·
qn–1.
► Например,
найдём седьмой член геометрической прогрессии 1, 2, 4, . . .
Имеем,
b1 = 1, q = 2,
b7 = b1 · q6
= 1 · 26 = 64. ◄
Так как
bn–1 = b1 ·
qn–2,
bn = b1 ·
qn–1,
bn+1 = b1 ·
qn,
то, очевидно,
bn2 = bn–1 · bn+1,
то есть,
каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.
► Например,
докажем, что последовательность, которая задаётся формулой bn = –3 · 2n, является геометрической прогрессией. Воспользуемся приведённым выше утверждением. Имеем:
bn = –3 · 2n,
bn–1 = –3 · 2n–1,
bn+1 = –3 · 2n+1.
Следовательно,
bn2 = (–3 · 2n)2 = (–3 · 2n–1) · (–3 · 2n+1) = bn–1 · bn+1,
что и доказывает нужное утверждение. ◄
Отметим, что n-й член геометрической прогрессии можно найти не только через b1, но и любой предыдущий член bk, для чего достаточно воспользоваться формулой
bn = bk ·
qn–k.
► Например,
для b5 можно записать
b5 = b1 ·
q4,
b5 = b2 ·
q3,
b5 = b3 ·
q2,
b5 = b4 ·
q. ◄
Так как
bn = bk ·
qn–k,
bn = bn–k ·
qk,
то, очевидно,
bn2 = bn–k · bn+k
то есть,
квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.
Кроме того, для любой геометрической прогрессии справедливо равенство:
bm · bn = bk · bl,
если
m + n = k + l.
► Например,
в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
1) b62 = 322 = 1024 = 16 · 64 = b5 · b7;
2) 1024 = b11 = b6 ·
q5 = 32 · 25 = 1024;
3) b62 = 322 = 1024 = 8 · 128 = b4 · b8;
4) b2 · b7 = b4 · b5, так как
b2 · b7 = 2 · 64 = 128,
b4 · b5 = 8 · 16 = 128. ◄
Сумма
Sn = b1 + b2 + b3 + . . . + bn
первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:
А при q = 1 — по формуле
Sn = nb1
Заметим, что если нужно просуммировать члены
bk, bk+1, . . . ,bn,
то используется формула:
| Sn – Sk–1 = bk + bk+1 + . . . + bn = bk · | 1 – qn–k+1 |
. |
| 1 – q |
► Например,
в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
S10 = 1 + 2 + . . . + 512 = 1 · (1 – 210) / (1 – 2) = 1023;
64 + 128 + 256 + 512 = S10 – S6 = 64 · (1 – 210–7+1) / (1 – 2) = 960. ◄
Если дана геометрическая прогрессия, то величины b1, bn, q, n и Sn связаны двумя формулами:
| bn = b1 · qn–1 и Sn = b1 · | 1 – qn |
. |
| 1 – q |
Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Для геометрической прогрессии с первым членом b1 и знаменателем q имеют место следующие свойства монотонности:
- прогрессия является возрастающей, если выполнено одно из следующих условий:
b1 > 0 и q > 1;
b1 < 0 и 0 < q < 1;
- прогрессия является убывающей, если выполнено одно из следующих условий:
b1 > 0 и 0 < q < 1;
b1 < 0 и q > 1.
Если q < 0, то геометрическая прогрессия является знакопеременной: её члены с нечётными номерами имеют тот же знак, что и её первый член, а члены с чётными номерами — противоположный ему знак. Ясно, что знакопеременная геометрическая прогрессия не является монотонной.
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
Pn = b1 · b2 · b3 · . . . · bn = (b1 · bn) n/2.
► Например,
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128)8/2 = 1284 = 268 435 456;
3 · 6 · 12 · 24 · 48 = (3 · 48)5/2 = (1441/2)5 = 125 = 248 832.◄
Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающей геометрической прогрессией называют бесконечную геометрическую прогрессию, модуль знаменателя которой меньше 1, то есть
|q| < 1.
Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю
–1 < q < 0.
При таком знаменателе последовательность знакопеременная. Например,
1, –1/2, 1/4, –1/8, . . . .
Суммой бесконечно убывающей геометрической прогрессии называют число, к которому неограниченно приближается сумма первых n членов прогрессии при неограниченном возрастании числа n. Это число всегда конечно и выражается формулой
| S = b1 + b2 + b3 + . . . = | b1 | . |
| 1 – q |
► Например,
10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 – 0,1) = 11 1/9 ,
10 – 1 + 0,1 – 0,01 + . . . = 10 / (1 + 0,1) = 9 1/11 . ◄
Связь арифметической и геометрической прогрессий
Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.
Если
a1, a2, a3, . . .— арифметическая прогрессия с разностью d, то
ba1, ba2, ba3, . . . — геометрическая прогрессия с знаменателем bd.
► Например,
1, 3, 5, . . . — арифметическая прогрессия с разностью 2 и
71, 73, 75, . . . — геометрическая прогрессия с знаменателем 72. ◄
Если
b1, b2, b3, . . .— геометрическая прогрессия с знаменателем q, то
loga b1, loga b2, loga b3, . . . — арифметическая прогрессия с разностью loga q.
► Например,
2, 12, 72, . . . — геометрическая прогрессия с знаменателем 6 и
lg 2, lg 12, lg 72, . . . — арифметическая прогрессия с разностью lg 6. ◄
Смотрите также:
Обозначения и сокращения
Таблицы чисел
Алгебраические тождества
Степени
Арифметический корень n-й степени
Логарифмы
Графики элементарных функций
Построение графиков функций геометрическими методами
Тригонометрия
Таблицы значений тригонометрических функций
Предел и непрерывность функции
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения