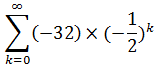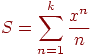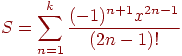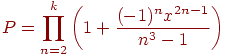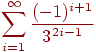Как найти сумму бесконечной последовательности элементов - Исправление недочетов и поиск решений вместе с Examum.ru

Бесконечно малые последовательности.

Начать изучение
Бесконечно большие последовательности.

Начать изучение
Арифметические операции над сходящимися последовательностями.

Начать изучение

Бесконечно малые последовательности.

Определение.

Последовательность ({alpha_{n}}) называется бесконечно малой, если
$$
displaystyle lim_{nrightarrowinfty}alpha_{n}=0.nonumber
$$

Это означает, что для любого (varepsilon>0) найдется номер (N=N_varepsilon) такой, что (|alpha_{n}-0|=|alpha_{n}| < varepsilon) для всех (ngeq N_varepsilon).

Понятие бесконечно малой последовательности используется для доказательства свойств сходящихся последовательностей. Пусть число (a) — предел последовательности ({x_{n}}). Обозначим (alpha_{n}=x_{n}-a). По определению предела
$$
forallvarepsilon>0 exists N_varepsilon: forall ngeq N_{varepsilon}rightarrow|x_{n}-a|=|alpha_{n}|<varepsilon,nonumber
$$
то есть ({alpha_{n}}) — бесконечно малая последовательность. Обратно: если (x_n=a+alpha_n), где ({alpha_{n}}) — бесконечно малая последовательность, то (displaystyle lim_{nrightarrowinfty}x_{n}=a).

Приведем примеры бесконечно малых последовательностей:

(displaystyle {a/n^{r}}, ainmathbb{R}, r=frac{1}{m}, minmathbb{N});
({q^{n}}, |q|<1);
({sqrt[n]{a}-1}, a>1);
({sqrt[n]{n}-1});
({n^{p}/a^{n}}, pinmathbb{N}, a>1).

При изучении свойств сходящихся последовательностей нам потребуется ввести арифметические операции над последовательностями. Назовем суммой, разностью, произведением и частным двух последовательностей ({x_{n}}) и ({y_{n}}) соответственно последовательности ({x_{n}+y_{n}}), ({x_{n}-y_{n}}), ({x_{n}y_{n}}), ({x_{n}/y_{n}}). При определении частного предполагается, что (y_nneq 0) для всех (ninmathbb{N}).

Бесконечно малые последовательности обладают следующими свойствами:

алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность;
произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.

Докажем это:

(circ) Пусть ({alpha_n}) и ({beta_n}) — бесконечно малые последовательности. Тогда для любого (varepsilon>0) существуют номера (N_1=N_{1}(varepsilon)) и (N_{2}=N_{2}(varepsilon)) такие, что (|alpha_{n}| < varepsilon/2) при всех (ngeq N_1) и (|beta_n| < varepsilon/2) при всех (ngeq N_{2}).Если (N=N_varepsilon=max(N_{1},N_{2})), то, используя неравенства для модуля суммы (разности), получаем для всех (ngeq N) неравенство
$$
|displaystyle alpha_{n}pmbeta_{n}|leq|alpha_{n}|+|beta_{n}|<frac{varepsilon}{2}+frac{varepsilon}{2}=varepsilon.nonumber
$$Следовательно, ({alpha_{n}pmbeta_{n}}) — бесконечно малая последовательность.Доказанное свойство с помощью индукции распространяется на любое число слагаемых.
Пусть ({alpha_{n}}) — ограниченная последовательность, ({beta_n}) — бесконечно малая последовательность. По определению ограниченной последовательности
$$
exists C>0:quadforall ninmathbb{N}rightarrow|alpha_{n}| < C,nonumber
$$
а по определению бесконечно малой последовательности
$$
displaystyle forallvarepsilon>0quadexists N_varepsilon:forall ngeq N_varepsilonrightarrow|beta_{n}|<frac{varepsilon}{C}.nonumber
$$
Отсюда следует, что
$$
displaystyle forall ngeq N_varepsilonrightarrow|alpha_{n}beta_{n}|=|alpha_{n}|cdot|beta_{n}|<frac{varepsilon}{C} C=varepsilon,nonumber
$$
то есть ({alpha_{n}beta_{n}}) — бесконечно малая последовательность. (bullet)

В частности, если ({alpha_{n}}) — стационарная последовательность, то есть (alpha_{n}=a) для всех (ninmathbb{N}), а ({beta_{n}}) — бесконечно малая последовательность, то ({alpha_nbeta_n}) — бесконечно малая последовательность.

Замечание.

Так как бесконечно малая последовательность ограничена, то из доказанного свойства следует, что произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Бесконечно большие последовательности.

Последовательность ({x_{n}}) называется бесконечно большой, если для любого (delta>0) существует такой номер (N_{delta}), что для всех (ngeq N_{delta}) выполняется неравенство (|x_{n}|>delta). В этом случае пишут (displaystyle lim_{nrightarrowinfty}x_n=infty) и говорят, что последовательность имеет бесконечный предел.

Используя логические символы, это определение можно записать так:
$$
displaystyle {lim_{nrightarrowinfty} x_{n}=infty}Leftrightarrowforalldelta>0 exists N_{delta}:forall ngeq N_{delta}rightarrow|x_{n}|>delta.label{ref1}
$$
Дадим геометрическую интерпретацию определения eqref{ref1}. Назовем (delta) — окрестностью (infty) (рис. 5.1) множество (E={xinmathbb{R}:|x|>delta}). Если

Рис. 5.1

последовательность ({x_n}) имеет бесконечный предел, то в любой (delta)-окрестности (infty) лежат все члены последовательности, за исключением, быть может, конечного числа членов.

Аналогично вводятся для последовательности ({x_n}) понятия бесконечного предела, равного (-infty) и (+infty) Эти пределы обозначаются соответственно символами (underset{nrightarrowinfty}{lim}x_n=-infty) и определяются так:
$$
{underset{nrightarrowinfty}{lim}x_n=-infty}Leftrightarrowforalldelta>0 exists N_{delta}: forall ngeq N_{delta}rightarrow x_{n}<-delta,label{ref2}
$$
$$
{underset{nrightarrowinfty}{lim}x_n=+infty}Leftrightarrowforalldelta>0 exists N_{delta}: forall ngeq N_{delta}rightarrow x_{n}>deltalabel{ref3}
$$

Множества (E_1={xinmathbb{R}: x < -delta}) и (E_2={xinmathbb{R}:x > delta}), где (delta > 0), назовем (delta)-окрестностями (-infty) и (+infty) соответственно (см. рис. 5.1). Тогда (E=E_{1}cup E_{2}).

Согласно определению eqref{ref3} последовательность ({x_n}) имеет предел, равный (+infty), если в (delta)-окрестности символа (+infty) содержатся все члены этой последовательности, за исключением, быть может, конечного числа их. Аналогичный смысл имеет определение eqref{ref2}.

В дальнейшем под пределом последовательности будем понимать конечный предел, если не оговорено противное.

Приведем примеры последовательностей, имеющих бесконечный предел:

если (x_{n}=-sqrt{n}), то (underset{nrightarrowinfty}{lim}x_n=-infty);
так как (x_{n}=n^{2}/(n+2)), то (underset{nrightarrowinfty}{lim}x_n=-infty);
если (x_{n}=(-1)^{n}2^{n}), то (underset{nrightarrowinfty}{lim}x_n=infty).

Арифметические операции над сходящимися последовательностями.

Теорема

Если (underset{nrightarrowinfty}{lim}x_n=a, underset{nrightarrowinfty}{lim}y_n=b), то:

(underset{nrightarrowinfty}{lim}(x_n+y_n)=a+b).
(underset{nrightarrowinfty}{lim}(x_ny_n)=ab).
(underset{nrightarrowinfty}{lim}frac{x_n}{y_n}=frac ab) при условии, что (y_nneq 0 (ninmathbb{N})) и (bneq 0).

Доказательство

(circ) Так как (underset{nrightarrowinfty}{lim}x_n=a, underset{nrightarrowinfty}{lim}y_n=b), тo (x_n=a+alpha_n, y_n=b+beta_n), где ({alpha_{n}}) и ({beta_{n}}) — бесконечно малые последовательности.

Из равенства (x_{n}+y_{n}=a+b+alpha_{n}+beta_{n}), где ({alpha_{n}+beta_{n}}) — бесконечно малая последовательность, следует, что (x_n+y_nrightarrow a+b) при (nrightarrowinfty).
Воспользуемся равенством
$$
x_ny_n=ab+abeta_{n}+balpha_{n}+alpha_{n}beta_{n}.nonumber
$$Так как ({alpha_{n}}) и ({beta_{n}}) — бесконечно малые последовательности, то последовательности ({abeta_n}, {balpha_n}) и ({alpha_nbeta_n}) также являются бесконечно малыми, откуда следует, что ({abeta_n+balpha_{n}+alpha_{n}beta_{n}}) — бесконечно малая последовательность. Поэтому (x_ny_nrightarrow ab) при (nrightarrowinfty).
Докажем, что (displaystyle {frac{x_{n}}{y_{n}}-frac{a}{b}}) — бесконечно малая последовательность. Имеем (displaystyle frac{x_{n}}{y_{n}}-frac{a}{b}=frac{(a+alpha_{n})b-(b+beta_{n})a}{by_{n}}=(alpha_{n}-frac{a}{b}beta_{n})frac{1}{y_{n}}). Так как ({alpha_{n}}) и ({beta_{n}}) бесконечно малые последовательности, то и последовательность (displaystyle {alpha_{n}-frac{a}{b}beta_{n}}) также является бесконечно малой.По условию (yrightarrow n) при (nrightarrow infty), где (bneq 0) и (y_nneq 0) для всех (ninmathbb{N}). Поэтому (смотри пример) последовательность (displaystyle {frac{1}{y_n}}) является ограниченной.Отсюда следует, что (displaystyle {(alpha_{n}-frac{a}{b}beta_{n})frac{1}{y_n}}) — бесконечно малая последовательность как произведение бесконечно малой последовательности на ограниченную последовательность.Таким образом, (displaystyle left{frac{x_n}{y_n}-frac abright}) — бесконечно малая последовательность, и поэтому (displaystyle frac{x_n}{y_n}rightarrowfrac{a}{b}) при (nrightarrowinfty.bullet)

Пример 1

Найти (underset{nrightarrowinfty}{lim}S_n), если (displaystyle S_n=sum_{k=1}^nfrac1{a_ka_{k+1}}), где ({a_k}) — арифметическая прогрессия, все члены и разность (d) которой отличны от нуля.

Решение

(trianglequad) Используя равенство
$$
S_{n}=displaystyle frac{1}{da_{1}}-frac{1}{d(a_{1}+nd)},nonumber
$$
полученное в примере, решенном ранее, находим (displaystyle lim_{nrightarrowinfty}S_{n}=frac{1}{da_{1}}quadblacktriangle).

Пример 2

Пусть (P_{k}(x)=a_{0}x^{k}+a_{1}x^{k-1}+ldots+a_{k-1}x+a_{k}), (Q_{k}(x)=b_{0}x^{k}+b_{1}x^{k-1}+ldots+b_{k-1}x+b_{k}), где (a_{0}neq 0), (b_{0}neq 0). Найти (displaystyle lim_{nrightarrowinfty}frac{P_{k}(n)}{Q_{k}(n)}).

Решение

(trianglequad) Разделив числитель и знаменатель дроби на (n^{k}), получаем
$$
displaystyle frac{P_{k}(n)}{Q_{k}(n)}=frac{a_{0}+a_{1}frac{1}{n}+ldots+a_{k}frac{1}{n^{k}}}{b_{0}+b_{1}frac{1}{n}+ldots+b_{k}frac{1}{n^{k}}}.nonumber
$$

Отсюда следует, что искомый предел равен (a_{0}/b_{0}), так как (a/n^{p}rightarrow 0) при (nrightarrowinfty) для любого (ainmathbb{R}) и любого (pinmathbb{N}) (см. пример). (blacktriangle)

Пример 3

Найти (underset{nrightarrowinfty}{lim}x_n), где (x_n=displaystyle frac{1}{n^{3}}sum_{k=1}^{n}k^{2}).

Решение

(trianglequad) Воспользуемся формулой (displaystyle sum_{k=1}^{n}k^{2}=frac{n(n+1)(2n+1)}{6}), полученной ранее (ссылка на пример). Тогда (displaystyle x_{n}=frac{1}{3}left(1+frac{1}{n}right)left(1+frac{1}{2n}right)) , откуда находим (displaystyle lim_{nrightarrowinfty}x_{n}=frac{1}{3}.quadblacktriangle)

Пример 4

Найти (displaystyle lim_{nrightarrowinfty}x_{n},quad x_{n}=sqrt{n^{2}+2n+3}-sqrt{n^{2}-2n+5}).

Решение

Так как
$$
x_{n}=displaystyle frac{(n^{2}+2n+3)-(n^{2}-2n+5)}{sqrt{n^{2}+2n+3}+sqrt{n^{2}-2n+5}}=frac{4-frac{2}{n}}{sqrt{1+frac{2}{n}+frac{3}{n^{2}}}+sqrt{1-frac{2}{n}+frac{5}{n^{2}}}},nonumber
$$
то, используя результат разобранного ранее примера, получаем (underset{nrightarrowinfty}{lim}x_n=2.blacktriangle)

Пример 5

Доказать, что последовательность ({x_{n}}), где (x_n=displaystyle frac{1}{sqrt{n^{2}+1}}+frac{1}{sqrt{n^{2}+2}}+ldots+frac{1}{sqrt{n^{2}+n}}), сходится, и найти ее предел.

Решение

(trianglequad) Так как в сумме (x_{n}) каждое слагаемое меньше предыдущего, то
$$
frac{n}{sqrt{n^{2}+n}},<,x_{n},<,frac{n}{sqrt{n^{2}+1}},nonumber
$$
или
$$
displaystyle frac{1}{sqrt{1+frac{1}{n}}},<,x_{n},<,frac{1}{sqrt{1+frac{1}{n^{2}}}}.nonumber
$$
Используя доказанную ранее теорему и результат разобранного ранее примера, получаем, что (displaystyle lim_{nrightarrowinfty}x_{n}=1.blacktriangle)

Источник

В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.

Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.

Сходящийся ряд

Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:

Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |a_n — a_n-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.

Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.

Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);

Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5^k.

Функцию f можно записать короче:

double f(int k)

{

return —32.0 * powf(—0.5, k);

}

Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.

float e;

printf(«e = «);

scanf_s(«%f», &e);

Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.

double previous, current;

double sum = 0;

int k = 0;

Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.

current = f(k);

sum += current;

k++;

Запись выражения sum += current; эквивалентна записи: sum = sum + current;

Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |a_n — a_n-1| > ε.

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

Сумма посчитана. Осталось вывести результат вычислений в консоль.

printf(«sum = %fn», sum);

В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:

#include <stdio.h>

#include <math.h>

#include <conio.h>

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

int main()

{

float e;

printf(«e = «);

scanf_s(«%f», &e);

double previous, current;

double sum = 0;

int k = 0;

current = f(k);

sum += current;

k++;

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

printf(«sum = %fn», sum);

_getch();

return 0;

}

Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.

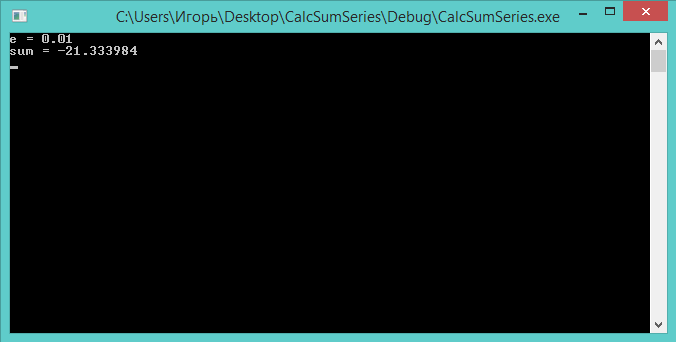
Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.

Скачать исходник

Источник

Вычисление бесконечных сумм

Будем
теперь рассматривать бесконечную сумму
вида
.
Это выражение называется функциональным
рядом. При различных значенияхиз
функционального ряда получаются
различные числовые ряды.
Числовой ряд может быть сходящимся или
расходящимся. Совокупность значений,
при которой функциональный ряд сходится,
называется его областью сходимости.

Числовой
ряд называется сходящимся, если сумма
n первых его членов
приимеет
предел, в противном случае, ряд называется
расходящимся. Ряд может сходиться лишь
при условии, что общий член рядапри
неограниченном увеличении его номера
стремится к нулю:.
Это необходимый признак сходимости для
всякого ряда.

В
случае бесконечной суммы будем вычислять
ее с заданной точностью
Cчитается,
что требуемая точность достигается,
если вычислена сумма нескольких первых
слагаемых и очередное слагаемое оказалось
по модулю меньше чеме,
то есть это слагаемое на результат
практически не влияет. Тогда его и все
последующие слагаемые можно не учитывать.

Пример.
Написать программу для подсчета суммы
с
заданной точностью().

Указание
по решению задачи.
Рассмотрим, что представляет из себя
заданный ряд:
.
Как видим, общий член ряда с увеличением
значения i стремится к нулю. Поэтому
данную сумму можно вычислить, но только
с определенной точностью.
Заметим также, что последовательность
слагаемых можно выразить с помощью
рекуррентного соотношения,,
а всю сумму — с помощью рекуррентного
соотношения.
(Данные рекуррентные соотношения
выведите самостоятельно.)

using
System;

namespace
Hello

{

class
Program

{

static
void Main()

{

Console.Write(«Задайте
точность вычислений е: «);

double
e=double.Parse(Console.ReadLine());

double
a=-1, s=0;

for
(int i=2; Math.Abs(a)>=e; ++i)

{

s+=a;

a/=-i;

}

Console.WriteLine(«s={0:f2}»,s);

}

Практическое задание

Замечание.
При решении задач производить обработку
следующих исключительных ситуаций:
ввода пользователем недопустимых
значений и переполнения при вычислении
математических выражений.

Для
заданного натурального
и
действительногоподсчитать
следующие суммы:
1. ;
2. ;
3. ;
Для
заданного натурального
и
действительногоподсчитать
следующие выражения:
Вычислить
бесконечную сумму ряда с заданной
точностью е (e>0).

Вычислить
и вывести на экран значение функции
на
отрезкеc
шагомс
точностьюРезультат
работы программы представить в виде
следующей таблицы:

№	Значение x	Значение функции F(x)	Количество просуммированных слагаемых n
1
2
…

Замечание.
При решении задачи использовать
вспомогательную функцию.

Лекция 8. Массивы

Данная
лекция рассматривает одномерные и
многомерные массивы. Приведено большое
количество практических примеров и
заданий.

Массив
— набор элементов одного и того же типа,
объединенных общим именем. Массивы в
С# можно использовать по аналогии с тем,
как они используются в других языках
программирования. Однако С#-массивы
имеют существенные отличия: они относятся
к ссылочным типам данных, более того —
реализованы как объекты. Фактически
имя массива является ссылкой на область
кучи (динамической памяти), в которой
последовательно размещается набор
элементов определенного типа. Выделение
памяти под элементы происходит на этапе
инициализации массива. А за освобождением
памяти следит система сборки мусора —
неиспользуемые массивы автоматически
утилизируются данной системой.

Рассмотрим
различные типы массивов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Формулы для нахождения суммы бесконечной геометрической прогрессии

Содержание:

Что такое геометрическая прогрессия
Бесконечная убывающая геометрическая прогрессия — что из себя представляет
Сумма первых n членов геометрической прогрессии
Как найти q в геометрической прогрессии
Примеры решения задач

Что такое геометрическая прогрессия

Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число (Xn), то говорят, что представлена числовая последовательность. Она имеет вид: (X_1, X_2)
,…,(X_n), или ({[X_n]}). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности (f(n)=X_n.)

Геометрическая прогрессия — последовательность с заданным первым членом (b_1), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число (q).

Числа ( b_1) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:

(b_n=b_{n-1}cdot q,)

Где (b_n) — (n-й) член прогрессии, (q) — знаменатель прогрессии.

Геометрическая прогрессия может быть задана рекуррентным соотношением:

(b_1=b,) (b_{n+1}=b_ncdot q,) (nin N,) (bneq0), (qneq0.)

Примечание

Рекуррентное соотношение задается формулой, выражающей (Xn) через предшествующие ему члены последовательности.

Примеры геометрических прогрессий:

1, 2, 4, 8, 16, 32 …; (b_1 = 1), (q = 2;)
1, 3, 9, 27, 81…; (b_1 = 1), (q = 3;)
2, -8, 32, -128, 512…:(b_1 = 2), (q = -4.)

Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:

(left|b_nright|=sqrt{b_{n-1}cdot b_{n+1}},) (ngeq2, )

или

(b_n^2=b_{n-1}cdot b_{n+1}.)

Если (b_1 > 0) и (q > 1) или (b_1 < 0) и (0 < q < 1), то для геометрической последовательности характерно возрастание.

Если (b_1 > 0) и 0 < (q < 1) или (b_1 < 0) и (q > 1), то для нее характерно убывание.

Примеры геометрических прогрессий в жизни:

Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
Начисление процентов по вкладу в банках может осуществляться по простой или сложной схеме: соответственно, проценты начисляются либо по арифметической, либо по геометрической прогрессиям.

Бесконечная убывающая геометрическая прогрессия — что из себя представляет

Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы (|q| <1.)

Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:

(S=frac{b_1}{1-q}.)

Доказательством этой формулы является то, что величина (q^n) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.

Пример такой прогрессии:

1, (frac12,) (frac14,) (frac18), (frac1{16},…)

Если (q=1), то для вычисления суммы (S_n) первых n членов геометрической прогрессии применяют следующую формулу:

(S_n=b_1+…+b_n=frac{b_1-b_nq}{1-q}=frac{b_1left(1-q^nright)}{1-q}.)

Если (q≠1), то формула видоизменяется в:

(S_n=b_1n.)

Также для объяснения формулы, введем другое обозначение суммы первых членов прогрессии:

(S_n=b_1+b_2+…+b_n.)

Тогда можно видоизменить формулу нахождения суммы (S_n) первых n членов геометрической прогрессии:

(S_n=b_1frac{q^n-1}{q-1}.)

Как найти q в геометрической прогрессии

Вычисление знаменателя прогрессии (q) осуществляют через выведение из формулы на нахождение общего члена геометрической прогрессии:

(b_n=b_1q^{n-1} )

Отсюда:

(q=frac{b_{n+1}}{b_n}.)

Примеры решения задач

Задача № 1

Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.

Найти знаменатель и первый член геометрической прогрессии.

Решение:

По условиям задачи:

(b_1+b_1q^2=35.,)

(b_1left(1+q+q^2+q^3+q^4right)=49left(frac1{b_1}+frac1{b_1q}+frac1{b_1q^2}+frac1{b_1q^3}+frac1{b_1q^4}right).) (2)

Так как (1+q+q^2+q^3+q^4neq0) (иначе задача теряет смысл), то равенство (2) можно записать в виде:

(b_1^2q^4=49. ) (3)

Из (3) следует, что либо (b_1q^2=7,) либо (b_1q^2=-7.)

Если равно 7, то из (1) находим (b_1=28,) (q^2={textstylefrac14}), откуда (q=pmfrac12 )

Если равно -7, (b_1=42,) (\q^2=-{textstylefrac16}). В этом случае второе условие задачи теряет смысл.

Конечный результат:

(b_1=28,) (q=pmfrac12. )

Задача № 2

(S_n) — сумма первых n членов геометрической прогрессии.

Доказать, что: (S_nleft(S_{3n}-S_{2n}right)=left(S_{2n}-S_nright)^2). (1)

Доказательство:

Пусть (b_k — k-й) член, (q)— знаменатель геометрической прогрессии. Тогда:

(S_{m+k}=S_m+b_1q^m+b_1q^{m+1}+…+b_1q^{m+k-1},)

откуда:

(S_{m+k}-S_m=q^mleft(b_1+b_1q+…+b_1q^{k-1}right))

или

(S_{m+k}-S_m=q^mS_k) (2).

Полагая в (2) сначала (m = 2_n,) (k = n), а затем (m = n), (k = n), получаем

(S_{3n}-S_{2n}=q^{2n}cdot S_n), (S_{2n}-S_n=q^ncdot S_n.) (3)

А из равенств (3) следует равенство (1).

Задача № 3

Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.

Найти первый член и знаменатель этой прогрессии.

Решение:

Обозначим: (b_1) — первый член, (S) — сумма прогрессии, (q) — знаменатель, (S_1) — сумма возведенных в третью степень ее членов.

Тогда

(S=frac{b_1}{1-q}),( S_1=frac{b_1^3}{1-q^3}.)

Далее получаем

(frac{S^3}{S_1}-frac{1-q^3}{{(1-q)}^3}=frac{4^3}{192}=frac13 )

(3(1+q+q^2)=1-2q+q^2,;qneq1..)
Полученное уравнение, записанное в виде

(2q^2+5q+2=0)

имеет корни (q_1 = −2,) (q_2 = − ½.)

Так как (|q| < 1), отбрасываем первый корень.

Следовательно:

(q=-frac12,;b_1=4(1-q)=6.)

Задача № 4

(S_n)первых трех членов геометрической прогрессии равна 351. (S_n) следующих трех членов равна 13.

Найти первый член и знаменатель прогрессии.

Решение:

Запишем условия задачи в виде системы уравнений:

(left{begin{array}{l}b_1+b_2+b_3=351,\b_4+b_5+b_6=13end{array}right.Leftrightarrow left{begin{array}{l}b_1+b_1q+b_1q^2=351,\b_1q^3+b_1q^4+b_1q^5=13end{array}right.Leftrightarrow left{begin{array}{l}b_1(1+frac13+frac19)=351,\q=frac13end{array}right.Leftrightarrowleft{begin{array}{l}frac{13}9b_1=351,\q=frac13end{array}Leftrightarrowleft{begin{array}{l}b_1=frac{351cdot9}{13}=243,\q=frac13.end{array}right.right..)

Ответ: (b_1=243,;q=frac13.)

Задача № 5

Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.

Найти знаменатель прогрессии?

Решение:

Определим, что в прогрессии 2n членов и (S_{2n}) — сумма всех членов, а (S_n^ast) — сумма членов, стоящих на нечетных местах.

Тогда (S_{2n}=frac{b_1(1-q^{2n})}{1-q}.)

(S_n^ast=b_1+b_3+…+b_{2n-1}=b_1+b_1q^2+…+b_1q^{2n-2}=frac{b_1(1-q^{2n)}}{1-q^2}.)

Где (b_1) — первый член прогрессии, а (q ≠ 1) — знаменатель прогрессии.

По условию задачи:

(S_{2n}=3S_n^astRightarrowfrac{b_1(1-q^{2n)}}{`1-q}=3frac{b_1(1-q^{2n)}}{1-q^2}Rightarrow1+q=3Rightarrow q=2.)

Ответ: (q=2. )

Источник

The infinite series formula is used to find the sum of an infinite number of terms, given that the terms are in infinite geometric progression with the absolute value of the common ratio less than 1. This is because, only if the common ratio is less than 1, the sum will converge to a definite value, else the absolute value of the sum will tend to infinity.

Formula

For a geometric series, we can express the sum as,

a + ar + ar² + ar³ + … + (infinite terms) = a/(1 – r)

where,

a = first term of the geometric series

r = common ratio, where -1 < r < 1

Conditions:

The series should be in geometric progression.
The absolute value of the common ratio should be less than 1.

Derivation of the Formula

Let’s consider,

a = first term of the geometric series

r = common ratio, where -1 < r < 1

Let us consider the sum of the geometric progression be S.

Then we can write,

S = a + ar + ar²+ ar³ + … —– (i)

Multiplying both sides of the equation by r, we get,

Sr = ar + ar² + ar³ + ar⁴ + … —– (ii)

Subtracting Eq. (ii) from Eq. (i), we get

S – Sr = (a + ar + ar²+ ar³) + … – (ar + ar² + ar³ + ar⁴ + …)

S(1 – r) = a

S = a/(1 – r)

Hence, the sum of infinite series of a geometric progression is a/(1 – r)

Note:

If the absolute value of the common ratio ‘r’ is greater than 1, then the sum will not converge.

Thus, the absolute value of the sum will tend to infinity. Thus, if r > 1,

| S | = | a + ar + ar² + ar³ + … | = ∞

Sample Problems

Question 1. Find the sum of the infinite series with first term 4 and common ratio 1/2.

Solution:

Given, the first term a = 4

The common ratio r = 1/2

Thus, we can write the series as,

S = 4 + 4 × (1/2) + 4 × (1/2)² + …

So, the sum will stand as

S = 4/(1 – (1 / 2)) = 4/(1/2) = 4 × 2 = 8

S = 8

So, the sum of the series is equal to 8.

Question 2. Find the sum of the infinite series 1 + (1/2) + (1/2)² + (1/2)³ + … .

Solution:

Given, the first term of the series a = 1.

The common ratio is r = 1/2.

Since the absolute value of the common ratio is less than 1, we can apply the general formula.

So, the sum is,

S = 1/(1 – (1/2)) = 2

So, the sum of the given infinite series is 2.

Question 3. Evaluate the sum 2 + 4 + 8 + 16 + … .

Solution:

We can write the sum of the given series as,

S = 2 + 2²+ 2³ + 2⁴ + …

We can observe that it is a geometric progression with infinite terms and first term equal to 2 and common ratio equals 2.

Thus, r = 2.

Since, the value of r > 1, the sum will not converge and tend to infinity. Thus,

S = + ∞

Question 4. Find the sum of the series 2 – 1/5 + 1 – 1/25 + 1/2 – 1/125 + … .

Solution:

We can write the sum of the series as the difference of two infinite series as:

S = (2 + 1 + 1/2 + 1/2² + …) – (1/5 + 1/25 + 1/125 + … )

S = (2 + 1 + 1/2 + 1/2² + …) – (1/5 + 1/5² + 1/5³ + …)

S = S1 – S2

where,

S1 = 2 + 1 + 1/2 + 1/2² + …

S2 = 1/5 + 1/5² + 1/5³ + …

Here, we can see both S1 and S2 are infinite summation of geometric series, where,

a1 = 2, r1 = 1/2

a2 = 1/5, r2 = 1/5

Thus, we can write,

S1 = 2/(1 – (1/2)) = 2/(1/2) = 4

S2 = (1/5)/(1 – (1/5)) = (1/5) / (4/5) = 1/4

So, the summation S stands as,

S = S1 – S2 = 4 – 1/4 = (16 – 1)/4 = 15/4 = 3.75

S = 3.75

Thus, the sum of the given series is 3.75 .

Last Updated :
29 Dec, 2021

Like Article

Save Article

Источник