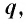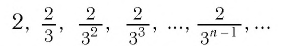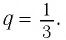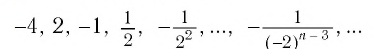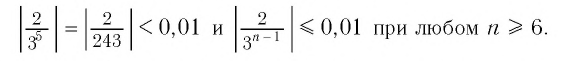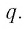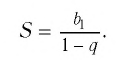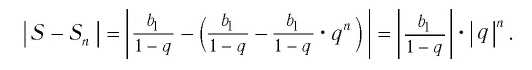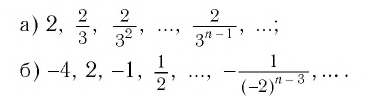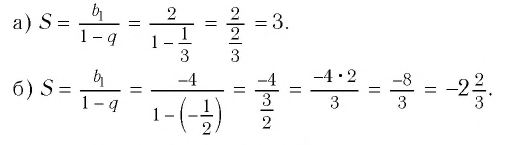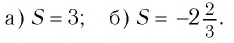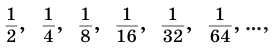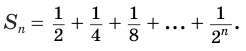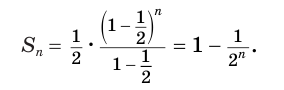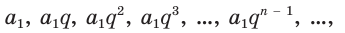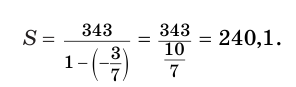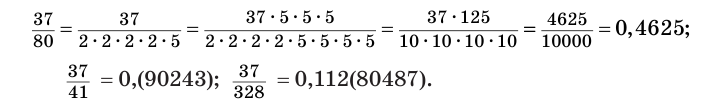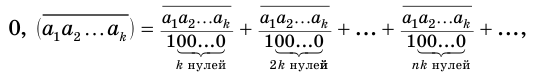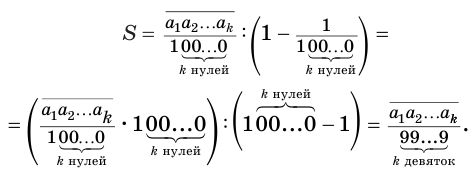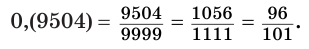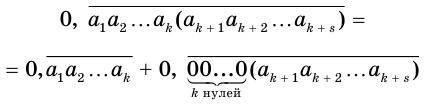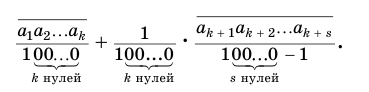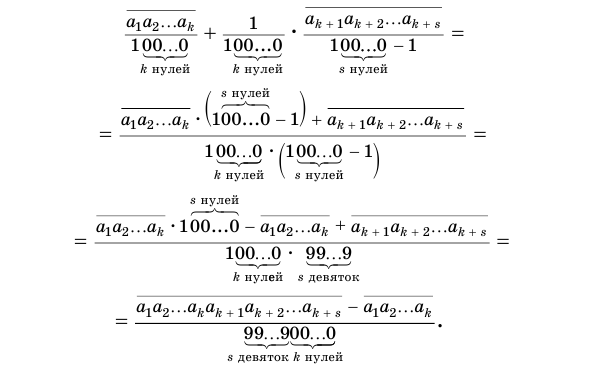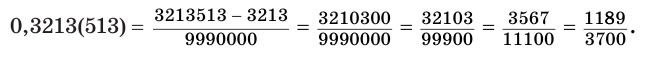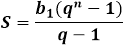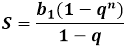Предметные цели:
создать методическими средствами
психолого-педагогические условия для усвоения
понятий:
- БУГП
- СУММА БУГП
и применения их при решении ключевых задач:
- Алгоритм распознавания БУГП
- Вычисление суммы БУГП.
Цели личностного развития:
установление содержательных связей БУГП с
элементами субъектного опыта учащихся в
изучении математики по линиям тождественных
преобразований, уравнений и действительных
чисел.
Ход занятия (занятие состоит из 2-х уроков)
Урок 1.
1 этап: Диагностика усвоения материала по
теме: “Действия с иррациональными числами”.
Самостоятельная работа, которая выполняется
индивидуально каждым учащимся. Оперативная
обратная связь осуществляется с помощью разбора
решений примеров непосредственно по окончании
самостоятельной работы.
Содержание самостоятельной работы:
(Задания приведены с ответами).
По окончании работы проводится анализ
результатов работы и оперативный разбор ошибок.
2 этап. Актуализация знаний, необходимых для
изучения нового материала.
Работа осуществляется в форме фронтальной
беседы с элементами организации поисковой
деятельности. Полученные результаты фиксируются
в тетрадях.
Содержание фронтальной работы:
1. Повторение:
а) определения понятия геометрической
прогрессии (ГП);
б) формулы n-ого члена ГП;
в) формулы суммы n первых членов ГП.
2. Получение нового результата:
Рассмотрим формулу суммы n первых членов ГП:
.
При 
эту формулу можно переписать в виде: 
или 
, из
чего следует формула
Положим в этом равенстве 
, тогда получим
,
домножим обе части равенства на 
,
получим
, а
отсюда вытекает полезное тождество:
(Доказательство приведенных формул см.
Виленкин Н.Я. и др. “Алгебра и математический
анализ. 10 класс”, М., “Просвещение”, 1992г., стр.45).
В результате обсуждения, в процессе которого
осуществляется конкретизация вновь полученного
обобщенного знания, учащиеся приходят к выводу,
что ранее изученные формулы разности квадратов и
суммы и разности кубов представляют собой
частные случаи выведенных формул:
Таким образом, удаётся установить
содержательную связь БУГП с линией
тождественных преобразований.
3 этап. Создание мотивации для формирования
понятий БУГП и суммы БГУП.
Особенный интерес представляет обсуждение
наглядной демонстрации существования суммы
бесконечного числа слагаемых. Работа
осуществляется фронтально, используются
элементы исследовательской деятельности.
Содержание этапа:
1. В процессе введения определения БУГП
рассматриваются особенности ГП с ¦q¦ < 1. Затем
формулируется определение БУГП и решаются
ключевые задачи распознавания БУГП:
а) в условии задана ГП; выяснить, является ли она
БУГП;
б) в условии задана последовательность;
выяснить, является ли она БГУП.
Вторая задача соответствует более высокому
уровню сложности: сначала требуется выяснить,
выяснить, является ли последовательность ГП;
затем — является ли она БУГП?
1) 
;
2) 
.
Эти задачи могут быть рассмотрены как а) и как
б). В процессе закрепления используются
упражнения:
15 (3)
Доказать, что ГП является бесконечно убывающей:
:-27, -9,
-3,…
16(3)
Выяснить, является ли ГП бесконечно убывающей: 
(см.Алимов и др.)
Для введения понятия суммы БУГП целесообразно
продолжить обсуждение задачи 2) и представить
сумму слагаемых с помощью графической
интерпретации:
Вывод формулы суммы БУГП проводится в
соответствии с материалом учебника Ш.А.Алимов и
др. “Алгебра и начала анализа.10-11”, М.,
“Просвещение”, 2003г., стр.11-14.
Обсуждение полученного результата создает
условия для психологического принятия наличия
конечной суммы бесконечного числа слагаемых.
Подводятся промежуточные итоги, на доску
выносятся основные результаты.
Урок 2 (продолжение).
4 этап. Формирование алгоритма вычисления
суммы БУГП.
Работа организована индивидуально у доски и в
тетрадях с дифференцированной степенью
самостоятельности. Критерием достижения
положительного результата этапа является знание
всеми учащимися алгоритма нахождения суммы БУГП.
Коррекция осуществляется с помощью
взаимопроверки. Используются упражнения
18(1,2) Найти сумму БУГП:
1. 
Ответ:
2. 
,
Ответ: 
а также упражнения из дидактических материалов
по алгебре и началам анализа Б.Г.Зива и В.А.
Гольдича, с/р №2, упражнения 1 из вариантов 1 и 2.
Найти сумму БУГП:
1. 
Ответ: 40,5
2. 
Ответ: 32.
Желающим, справившимся с общим заданием раньше
других, предлагается обратная задача:
Известна сумма БУГП и второй член прогрессии.
Нужно найти первый член прогрессии и
знаменатель:
дано: 
=-0,5; S=1,6;
найти q и 
.
За самостоятельное решение этой задачи
выставляется отдельная оценка.
5 этап. Первичное обобщение и включение нового
знания в систему субъектного опыта учащихся.
Установление содержательных взаимосвязей БУГП
с линиями уравнений и действительных чисел.
Фронтально решается задача распознавания БГУП.
С помощью этой задачи, с одной стороны,
осуществляется диагностика достижения
положительного результата предыдущих этапов
урока, с другой стороны, полученные результаты
позволяют осуществить содержательные
взаимосвязи по выше указанным линиям.
Из предложенных последовательностей выбрать
БУГП:
1) =3;
q=2.
2) 
=-4;
q=
.
3) 4;2;1; и т.д.;
4)=1; q=x; x>2;
5)=
; q=
.
6) =
; q=
.
7) =
; q=
=1; q=x; ¦x¦<1.
Таковыми являются 2); 3); 5); 6); 7) и 8).
Сначала найдём сумму БУГП из задания 8). Для
этого запишем сумму членов прогрессии и
воспользуемся формулой суммы БУГП. Получим:
1+
+
+ …+
+ …= 
.
Установление содержательных взаимосвязей БУГП
с линией уравнений
Сравните полученный результат с уравнением и
воспользуйтесь при его решении полученным
результатом:
Уравнение 1) 
; ¦x¦<1.
Заметим, что если к обеим частям равенства
прибавить 1, то можно воспользоваться полученным
выше результатом:
.
Итак, мы получили дробное рациональное
уравнение, алгоритм решения которого известен
школьникам.
Уравнение 2) 2
+ 1 + — 
+ 
— 
+ …= 
¦x¦<1.
Решение уравнения 1) проводится учеником на
доске, уравнение 2 предлагается для
самостоятельной работы дома.
Делается весьма неожиданный вывод о том, что
сумма БГУП даёт возможность решения некоторых
уравнений, имеющих бесконечное число членов.
Таким образом, удаётся установить
содержательную связь БУГП с линией уравнений.
Установление содержательных взаимосвязей БУГП
с линией действительных чисел.
К доске приглашаются 3 ученика для решения
задач 1-3.
1)=; q=.
Сначала находим сумму БУГП по формуле
S=
=
.
Затем попытаемся осмыслить, что представляет
собой сумма членов этой прогрессии, если её члены
записать в виде десятичных дробей:
0,3+0,03+0,003+….=0,3333…=0,(3).
Таким образом, видим, что с помощью формулы
суммы БУГП можно осуществлять переход от записи
действительного числа в виде бесконечной
периодической дроби к записи в виде обыкновенной
дроби.
2) =; q=.
Эта задача носит дублирующий характер и
используется для создания условий лучшего
осмысления сформулированного вывода.
3) =; q=
Решение этой задачи помогает понять, сколько
десятичных знаков содержит период дроби, какие
особенности решения возникают в связи с этим.
Решение этих задач даёт возможность
установления содержательной связи БУГП с линией
действительного числа.
После решения этих задач подводятся итоги
урока, предлагается домашнее задание:№20,21(2,4), 22(2),
23(2) из учебника Алимова.
Этап 6. Диагностика достижения положительного
результата урока.
Предлагается срезовая работа, которая
позволяет оценить достижение всеми учащимися уровня
образовательного стандарта.
Вариант 1.№№ 13(1); 15(1); 18(1); 19(1); 20(1).
Вариант 2.№№ 13(2); 15(2); 18(2); 19(2); 20(2).
Решение проводится учащимися в тетрадях,
проверяются только специальные бланки (Приложение
1), в которые вписываются ответы. Данная форма
позволяет осуществить оперативную обратную
связь и, в случае необходимости, провести
коррекцию.
Подводятся окончательные итоги урока,
сообщаются и комментируются оценки, полученные
школьниками.
Приложение 1.
| Класс | Фамилия, имя. | Оценка: | |||
| № задания | 1 | 2 | 3 | 4 | 5 |
| Ответ |
Формулы для нахождения суммы бесконечной геометрической прогрессии
Содержание:
- Что такое геометрическая прогрессия
- Бесконечная убывающая геометрическая прогрессия — что из себя представляет
- Сумма первых n членов геометрической прогрессии
- Как найти q в геометрической прогрессии
- Примеры решения задач
Что такое геометрическая прогрессия
Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число (Xn), то говорят, что представлена числовая последовательность. Она имеет вид: (X_1, X_2)
,…,(X_n), или ({[X_n]}). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности (f(n)=X_n.)
Геометрическая прогрессия — последовательность с заданным первым членом (b_1), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число (q).
Числа ( b_1) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:
(b_n=b_{n-1}cdot q,)
Где (b_n) — (n-й) член прогрессии, (q) — знаменатель прогрессии.
Геометрическая прогрессия может быть задана рекуррентным соотношением:
(b_1=b,) (b_{n+1}=b_ncdot q,) (nin N,) (bneq0), (qneq0.)
Примечание
Рекуррентное соотношение задается формулой, выражающей (Xn) через предшествующие ему члены последовательности.
Примеры геометрических прогрессий:
- 1, 2, 4, 8, 16, 32 …; (b_1 = 1), (q = 2;)
- 1, 3, 9, 27, 81…; (b_1 = 1), (q = 3;)
- 2, -8, 32, -128, 512…:(b_1 = 2), (q = -4.)
Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:
(left|b_nright|=sqrt{b_{n-1}cdot b_{n+1}},) (ngeq2, )
или
(b_n^2=b_{n-1}cdot b_{n+1}.)
Если (b_1 > 0) и (q > 1) или (b_1 < 0) и (0 < q < 1), то для геометрической последовательности характерно возрастание.
Если (b_1 > 0) и 0 < (q < 1) или (b_1 < 0) и (q > 1), то для нее характерно убывание.
Примеры геометрических прогрессий в жизни:
- Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
- Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
- Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
- Начисление процентов по вкладу в банках может осуществляться по простой или сложной схеме: соответственно, проценты начисляются либо по арифметической, либо по геометрической прогрессиям.
Бесконечная убывающая геометрическая прогрессия — что из себя представляет
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы (|q| <1.)
Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:
(S=frac{b_1}{1-q}.)
Доказательством этой формулы является то, что величина (q^n) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.
Пример такой прогрессии:
1, (frac12,) (frac14,) (frac18), (frac1{16},…)
Если (q=1), то для вычисления суммы (S_n) первых n членов геометрической прогрессии применяют следующую формулу:
(S_n=b_1+…+b_n=frac{b_1-b_nq}{1-q}=frac{b_1left(1-q^nright)}{1-q}.)
Если (q≠1), то формула видоизменяется в:
(S_n=b_1n.)
Также для объяснения формулы, введем другое обозначение суммы первых членов прогрессии:
(S_n=b_1+b_2+…+b_n.)
Тогда можно видоизменить формулу нахождения суммы (S_n) первых n членов геометрической прогрессии:
(S_n=b_1frac{q^n-1}{q-1}.)
Как найти q в геометрической прогрессии
Вычисление знаменателя прогрессии (q) осуществляют через выведение из формулы на нахождение общего члена геометрической прогрессии:
(b_n=b_1q^{n-1} )
Отсюда:
(q=frac{b_{n+1}}{b_n}.)
Примеры решения задач
Задача № 1
Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.
Найти знаменатель и первый член геометрической прогрессии.
Решение:
По условиям задачи:
(b_1+b_1q^2=35.,)
(b_1left(1+q+q^2+q^3+q^4right)=49left(frac1{b_1}+frac1{b_1q}+frac1{b_1q^2}+frac1{b_1q^3}+frac1{b_1q^4}right).) (2)
Так как (1+q+q^2+q^3+q^4neq0) (иначе задача теряет смысл), то равенство (2) можно записать в виде:
(b_1^2q^4=49. ) (3)
Из (3) следует, что либо (b_1q^2=7,) либо (b_1q^2=-7.)
Если равно 7, то из (1) находим (b_1=28,) (q^2={textstylefrac14}), откуда (q=pmfrac12 )
Если равно -7, (b_1=42,) (\q^2=-{textstylefrac16}). В этом случае второе условие задачи теряет смысл.
Конечный результат:
(b_1=28,) (q=pmfrac12. )
Задача № 2
(S_n) — сумма первых n членов геометрической прогрессии.
Доказать, что: (S_nleft(S_{3n}-S_{2n}right)=left(S_{2n}-S_nright)^2). (1)
Доказательство:
Пусть (b_k — k-й) член, (q)— знаменатель геометрической прогрессии. Тогда:
(S_{m+k}=S_m+b_1q^m+b_1q^{m+1}+…+b_1q^{m+k-1},)
откуда:
(S_{m+k}-S_m=q^mleft(b_1+b_1q+…+b_1q^{k-1}right))
или
(S_{m+k}-S_m=q^mS_k) (2).
Полагая в (2) сначала (m = 2_n,) (k = n), а затем (m = n), (k = n), получаем
(S_{3n}-S_{2n}=q^{2n}cdot S_n), (S_{2n}-S_n=q^ncdot S_n.) (3)
А из равенств (3) следует равенство (1).
Задача № 3
Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.
Найти первый член и знаменатель этой прогрессии.
Решение:
Обозначим: (b_1) — первый член, (S) — сумма прогрессии, (q) — знаменатель, (S_1) — сумма возведенных в третью степень ее членов.
Тогда
(S=frac{b_1}{1-q}),( S_1=frac{b_1^3}{1-q^3}.)
Далее получаем
(frac{S^3}{S_1}-frac{1-q^3}{{(1-q)}^3}=frac{4^3}{192}=frac13 )
(3(1+q+q^2)=1-2q+q^2,;qneq1..)
Полученное уравнение, записанное в виде
(2q^2+5q+2=0)
имеет корни (q_1 = −2,) (q_2 = − ½.)
Так как (|q| < 1), отбрасываем первый корень.
Следовательно:
(q=-frac12,;b_1=4(1-q)=6.)
Задача № 4
(S_n)первых трех членов геометрической прогрессии равна 351. (S_n) следующих трех членов равна 13.
Найти первый член и знаменатель прогрессии.
Решение:
Запишем условия задачи в виде системы уравнений:
(left{begin{array}{l}b_1+b_2+b_3=351,\b_4+b_5+b_6=13end{array}right.Leftrightarrow left{begin{array}{l}b_1+b_1q+b_1q^2=351,\b_1q^3+b_1q^4+b_1q^5=13end{array}right.Leftrightarrow left{begin{array}{l}b_1(1+frac13+frac19)=351,\q=frac13end{array}right.Leftrightarrowleft{begin{array}{l}frac{13}9b_1=351,\q=frac13end{array}Leftrightarrowleft{begin{array}{l}b_1=frac{351cdot9}{13}=243,\q=frac13.end{array}right.right..)
Ответ: (b_1=243,;q=frac13.)
Задача № 5
Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.
Найти знаменатель прогрессии?
Решение:
Определим, что в прогрессии 2n членов и (S_{2n}) — сумма всех членов, а (S_n^ast) — сумма членов, стоящих на нечетных местах.
Тогда (S_{2n}=frac{b_1(1-q^{2n})}{1-q}.)
И
(S_n^ast=b_1+b_3+…+b_{2n-1}=b_1+b_1q^2+…+b_1q^{2n-2}=frac{b_1(1-q^{2n)}}{1-q^2}.)
Где (b_1) — первый член прогрессии, а (q ≠ 1) — знаменатель прогрессии.
По условию задачи:
(S_{2n}=3S_n^astRightarrowfrac{b_1(1-q^{2n)}}{`1-q}=3frac{b_1(1-q^{2n)}}{1-q^2}Rightarrow1+q=3Rightarrow q=2.)
Ответ: (q=2. )
Рассмотрим бесконечную геометрическую прогрессию b1,b2,b3…bn…
Bычислим суммы двух, трёх, четырёх и т. д. членов прогрессии:
S1=b1;S2=b1+b2;S3=b1+b2+b3…Sn=b1+b2+b3+…+bn…
Получилась последовательность S1,S2,S3…Sn…
Эта последовательность может сходиться или расходиться, как и любая другая числовая последовательность.
Если последовательность Sn сходится к пределу S, тогда число S называют суммой геометрической прогрессии (не следует путать с суммой n членов геометрической прогрессии).
В случае, когда эта последовательность расходится, то о сумме геометрической прогрессии не говорят, однако сумму первых n членов геометрической прогрессии вычислить можно.
Формула суммы первых n членов геометрической прогрессии:
если Sn=b1+b2+…+bn, то Sn=b1(qn−1)q−1.
Если знаменатель
q
геометрической прогрессии
(bn)
удовлетворяет неравенству
q<1
, то сумма прогрессии
S
существует и вычисляется по формуле
limn→∞Sn=b11−q
.
Содержание:
Определение:
Геометрическая прогрессия со знаменателем 
Примеры бесконечно убывающих геометрических прогрессий
Приведем примеры бесконечно убывающих геометрических прогрессий.
Пример №1
Последовательность
является бесконечно убывающей геометрической прогрессией с
первым членом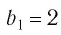 
и знаменателем 
Пример №2
Последовательность
является бесконечно убывающей геометрической прогрессией с первым членом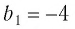 
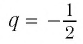
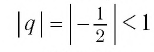
и знаменателем 
(здесь 
). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).
Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением 
этот модуль становится меньше любого заданного положительного числа.
Например, если мы зададим число 0,01, то
Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).
И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.
Например, если мы зададим число 0,001, то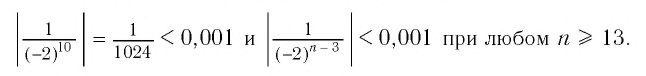 
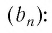
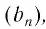
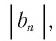
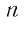
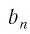
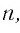
Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии 
чем больше номер п члена прогрессии 
тем меньше 
и с увеличением 
этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:
стремится к нулю при 
стремящемся к бесконечности.
Заметим, что если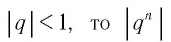 
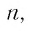
стремится к нулю при 
стремящемся к бесконечности.
Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членом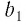
и знаменателем 
Запишем формулу суммы первых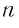 
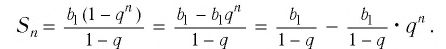
членов этой прогрессии и преобразуем это выражение: 
Обозначим
Тогда получим
Так как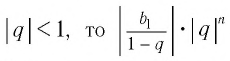 
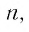
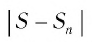
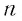
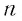
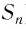
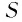
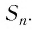
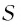
стремится к нулю при 
стремящемся к бесконечности. Значит, 
стремится к нулю при 
, стремящемся к бесконечности, т. е. чем больше число (чем больше слагаемых в сумме 
), тем меньше разница между 
и 
Поэтому число 
называют суммой бесконечно убывающей геометрической прогрессии.
Пример №3
Найти сумму бесконечно убывающей геометрической прогрессии:
Решение:
Ответ: 
- Заказать решение задач по высшей математике
Всё о бесконечно убывающей геометрической прогрессии
Пример:
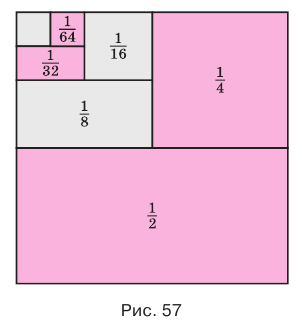
Рассмотрим квадрат со стороной 1 (рис. 57). Если середины его противоположных сторон соединить отрезком, то возникнут два прямоугольника с площадью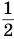 
.
Если теперь середины одного из полученных прямоугольников соединить отрезком, то получится два прямоугольника с площадью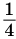 
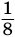
. Снова повторив такое действие, получим два прямоугольника с площадью 
. Будем продолжать этот процесс далее. В результате получим бесконечную убывающую последовательность
у которой каждый следующий член получается из предыдущего умножением на .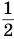
Естественно считать, что сумма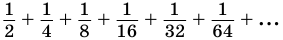 
равна 1, так как она представляет площадь всего данного квадрата.
Записанная сумма содержит бесконечно много слагаемых. Рассмотрим ее часть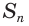 
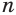
из 
слагаемых:
Ее компоненты образуют геометрическую прогрессию со знаменателем 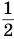. Поэтому
С возрастанием значения переменной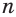 
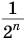
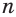
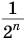
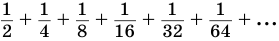
значение выражения 
становится все меньше и меньше: значение переменной всегда можно подобрать так, что значение выражения станет меньше любого малого заранее выбранного числа. Поэтому бесконечную сумму 
считают равной 1.
Рассмотрим теперь бесконечную геометрическую прогрессию
где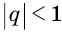 
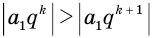
. Для таких прогрессий истинно условие 
, их называют бесконечно убывающими геометрическими прогрессиями.
Сумма бесконечно убывающей геометрической прогрессии
Суммой членов бесконечно убывающей геометрической прогрессии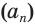 
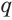
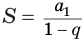
со знаменателем 
называется число 
.
Это определение объясняется тем, что с увеличением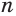 
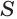
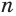
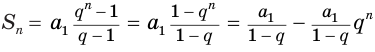
число 
все меньше отличается от суммы первых 
членов этой прогрессии. Действительно,
.
Поскольку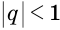 
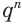
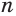
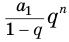
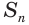
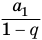
, то 
с увеличением приближается к нулю, а значит, приближается к нулю и вычитаемое 
. Поэтому сумма 
приближается к 
.
Пример №4
Найдем значение суммы 
.
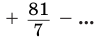
Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой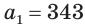 
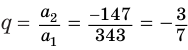
и 
. Поэтому
Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:
Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.
Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.
В дальнейшем мы будем пользоваться записью вида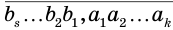 
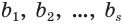
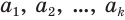
. Она обозначает десятичную дробь, целая часть которой записана с помощью цифр 
, а дробная — с помощью цифр 
.
Теорема 7.
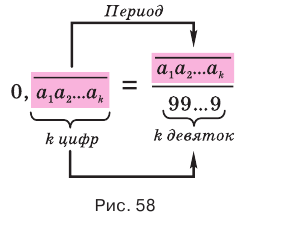
Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.
Доказательство:
Пусть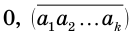 
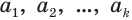
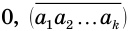
— периодическая десятичная дробь, где 
— цифры периода. Тогда число 
можно представить бесконечной суммой:
в которой каждое слагаемое получается из предыдущего умножением на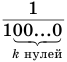 
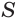
. Это означает, что бесконечную периодическую дробь можно рассматривать как сумму 
членов бесконечно убывающей геометрической прогрессии с первым
членом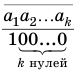 
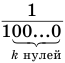
и знаменателем 
. Поэтому
Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.
Пример №5
Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:
Теорема 8.
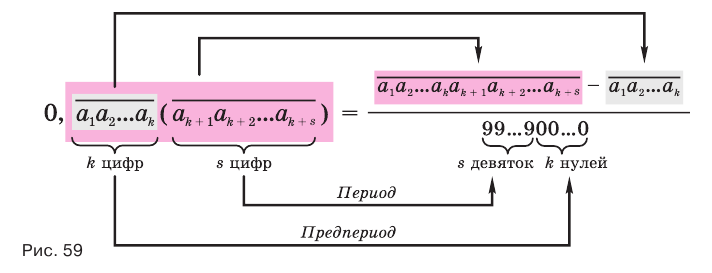
Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.
Доказательство:
Пусть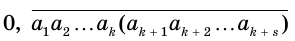 
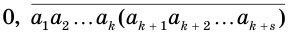
— периодическая десятичная дробь, где 
— цифры предпериода, 
— цифры периода. Тогда число 
можно представить суммой
или, с учетом теоремы 7, суммой
Преобразуем полученное выражение:
Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом, который отражен на схеме, представленной на рисунке 59.
Пример №5
Представим обыкновенной дробью десятичную дробь 0,3213(513). Имеем:
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем
- Логарифм — формулы, свойства и примеры
- Корень n-й степени
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
Сумма геометрической прогрессии имеет несколько различных представлений, которые зависят от знаменателя прогрессии. Для возрастающей положительной, отрицательной или знакочередующейся прогрессии имеет место исключительно сумма нескольких первых членов геометрической прогрессии, количество которых должно быть ограничено, так как сама последовательность будет бесконечной.
Для прогрессии, знаменатель которой заключен между нулем и единицей, то есть является правильной дробью (0<к<1), сумма всей последовательности будет вполне однозначным конкретным числом, так как весь числовой ряд будет убывающим. Сумма бесконечно убывающей геометрической прогрессии имеет свою отдельную формулу, которую можно найти в соответствующем разделе, вместе с калькулятором.
Чтобы найти сумму первых членов геометрической прогрессии, необходимо знать первый член и знаменатель прогрессии. Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.
Формула суммы первых трех, четырех или n членов геометрической прогрессии выводится с использованием среднего геометрического, как основного свойства данной прогрессии. Любое из чисел, стоящих в ряду, будет равно среднему геометрическому его соседей:
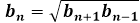
Если объединить это свойство с отношением двух последовательных членов прогрессии, которые неизменно равно одному и тому же числу — знаменателю, то путем нехитрых сокращений, сумма первых нескольких членов геометрической прогрессии приводится к такому виду:
В некоторых источниках встречается похожий вариант, но с другими знаками в скобках — по сути окончательного значения это не меняет, и для ручного расчета, когда даны первые несколько членов, уместно использовать более удобную на момент формулу.
